2.1. Curvas definidas implícitamente en el plano
( \newcommand{\kernel}{\mathrm{null}\,}\)
\newcommand{\conj}[1]{\overline{}[1]}}
\newcommand{\vector}[1]{\vec{\textbf {}[1]}}}
\newcommand{\abs}[1]{\left\vert {#1} \right\vert}}
\newcommand{\vectork}{\vector{\mathbf{k}})
\newcommand{\vectorrp}{\vector r}\,{}'}
\newcommand{\vectorrs}{\vector r}\,{}''}
\newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}
\newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}
\newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}
\newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}
\newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}
\newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}
\newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}
\newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}
\newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}
\newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}
\newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}
\newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}
\newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}
\newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}
Planteamiento del problema
A lo largo de tus estudios previos de matemáticas has ido viendo, fundamentalmente, curvas dadas por una ecuación y=y(x), pero también te has encontrado con ejemplos de curvas planas definidas como los puntos (x,y) que cumplen una cierta ecuación F(x,y)=0 que establece una relación entre las variables x e y. Dichas curvas reciben el nombre de curvas definidas implícitamente y la ecuación F(x,y)=0 se llama ecuación implícita de la curva. El ejemplo más habitual es la circunferencia de radio r>0, dada por la ecuación implícita x2+y2=r2 o, de forma equivalente, F(x,y)=x2+y2−r2=0. Otros ejemplos son las cónicas, las soluciones de algunas ecuaciones diferenciales de variables separadas o las curvas de nivel de un campo escalar.
Para la circunferencia x2+y2=r2 habrás visto que, según convenga, se puede trabajar con esta ecuación despejando una de las variables en función de la otra o hallando una parametrización, pero eso puede ser muy complicado o imposible en otros casos; veamos un ejemplo. Si consideramos la ecuación F(x,y)=y5+16y−32x3+32x=0 y utilizamos una aplicación como Desmos, u otra similar, para dibujar la curva formada por los puntos (x,y) que cumplen dicha ecuación, obtenemos la siguiente figura.

La curva de ecuación y5+16y−32x3+32x=0.
Aparentemente, es posible representar esta curva en la forma y=y(x). Para hacerlo tendríamos que despejar y de y5+16y−32x3+32x=0. Observemos que, fijado un valor de x, la ecuación g(y)=y5+16y−32x3+32x=0 tiene una única solución en y porque g(y) es un polinomio de grado 5, que pasa de negativo cuando y→−∞ a positivo cuando y→+∞, y que es estrictamente creciente porque su derivada g′(y)=5y4+16 es estrictamente positiva. Por tanto, la ecuación y5+16y−32x3+32x=0 tiene una única solución que depende del valor de x fijado, digamos y(x) y se dice que la ecuación F(x,y)=y5+16y−32x3+32x=0 define implícitamente la variable y como función y(x) de la variable x.
Sin embargo que la ecuación y5+16y−32x3+32x=0 tenga una única solución y(x) para cada valor de x no quiere decir que seamos capaces de despejar la y de manera efectiva, o sea, hallar y(x) como una fórmula. Para algunos valores de x aislados, como x=−1,0,1 sí podemos obtener fácilmente y(x), que vale cero en los tres casos y(−1)=y(09=y(1)=0. En otros puntos, para hallar y(2) por ejemplo, sustituimos x=2 en la ecuación, que nos queda y5+16y−192=0 y se puede resolver con el método de Newton, obteniendo y≈2.72. Esto nos permite determinar valores aproximados de y(x) en puntos concretos pero, como decíamos, esta forma de trabajar no nos sirve para usar y(x) como una función definida mediante una fórmula que podamos derivar o integrar.
En este ejemplo vemos que en todos los puntos de la curva se puede despejar y en función de x. Esto no siempre es así: la circunferencia de ecuación x2+y2=1 es el caso típico de curva definida implícitamente en la que no es posible despejar una de las variables para representar toda la circunferencia mediante una ecuación del tipo y=y(x) o una del tipo x=x(y); como mucho, podemos aspirar a representar así un trozo de la circunferencia. Por ejemplo, cerca del punto A=(0.6,0.8) podemos despejar la y para obtener y=√1−x2 y se dice que la ecuación x2+y2=1 define implícitamente la variable y como función de x cerca del punto A. Asimismo, cerca de A podemos despejar x=√1−y2 como función de y. Sin embargo, hay puntos en los que solamente podemos despejar una de las variables como función de la otra. Por ejemplo, por ambos lados del punto B=(1,0) sólo podemos despejar la x en función de la y pero no la y en función de la x.
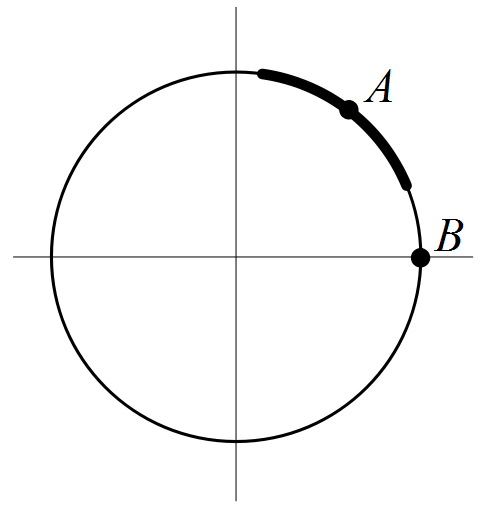
A ambos lados del punto A se puede despejar y=√1−x2; a ambos lados del punto B no se puede.
Un problema más delicado a la hora de analizar si las soluciones de una ecuación F(x,y)=0 forman una curva es que no siempre ocurre así. Por ejemplo, la ecuación x2+y2=0 representa un punto, mientras que las soluciones de x2−y4=0 forman dos parábolas que se tocan en el origen. En este último caso, si bien las soluciones no forman globalmente una curva explícita y=y(x), sí se puede decir que las soluciones de la ecuación x2−y4=0 que están lo suficientemente cerca del punto A=(−1,1) sí forman, al menos, un tramo de curva, el tramo de la parábola dada por y=x2 con, digamos, −1.5<x<−0.5. Es decir, la respuesta a la pregunta de si las soluciones de una ecuación F(x,y)=0 forman una curva dada explícitamente (bien por y=y(x), bien x=x(y)) puede ser negativa de forma global, viendo todas las soluciones como un conjunto del plano, pero afirmativa de forma local, viendo solo las soluciones que están cerca de un punto.
Un segundo problema es que pudiera ser posible despejar y=y(x) de F(x,y)=0 (al menos cerca de un punto) pero no, en la práctica, encontrar la fórmula y(x) explícitamente, como en el ejemplo y5+16y−32x3+32x=0 visto antes. Estudiaremos en esta sección cómo podemos calcular las derivadas de dichas funciones explícitas para poder generar sus polinomios de Taylor, por ejemplo.
En las siguentes secciones extenderemos nuestro estudio del caso plano al caso tridimensional en el que tenemos las variables x,y,z ligadas por una ecuación, como en el caso de la esfera x2+y2+z2=1, o bien dos ecuaciones, como en el caso de la curva de Viviani, dada por las ecuaciones x2+y2+z2=1 y x2+y2=y.
Observación clave. La propiedad de normalidad del gradiente que vimos en la Sección 1.6 nos da la pista para ver qué es razonable exigir como condición para que F(x,y)=0 represente una curva y podamos hallar sus elementos principales. Dada una función escalar de dos variables F(x,y) de clase C1, consideremos la ecuación F(x,y)=0, que podemos ver como la curva de nivel 0 del campo F. Si cerca de un punto (x,y) que cumple la ecuación pudiéramos despejar y=y(x) como función derivable de x, entonces la curva de nivel sería en ese tramo una curva regular y (1,y′(x)) sería un vector tangente a la curva. Por la propiedad de normalidad del gradiente, se tendría que Fx(x,y(x))+y′(x)Fy(x,y(x))=0, con lo cual y′(x)=−Fx(x,y(x))/Fy(x,y(x)), así que exigir Fy≠0 es una condición natural. Esta condición equivale a que la tangente no sea vertical, lo que en el ejemplo de la circunferencia visto antes corresponde exactamente a que podamos despejar y en función de x cerca del punto. El teorema de la función implícita asegura que eso es cierto en general.
Teorema de la función implícita para una curva en el plano o para una ecuación con dos variables.
Teorema de la función implícita (2D). Sea F(x,y) una función de clase Cn en una región U del plano. Sea (x0,y0) un punto interior del dominio U tal que F(x0,y0)=0 y ∂F∂y(x0,y0)≠0. Entonces existen un intervalo I centrado en el punto x0 y una única función y:I→R de clase Cn(I) tal que y(x0)=y0 e y=y(x) es una solución de la ecuación F(x,y)=0 para cada x∈I, o sea, F(x,y(x))=0 para cada x∈I. Además, usando la regla de la cadena, la derivada y′ viene dada por
y′(x)=−∂F(x,y(x))∂x/∂F(x,y(x))∂ypara cada x∈I.
Se dice, en este caso, que la ecuación F(x,y)=0 define implícitamente la variable y como función de x cerca del punto (x0,y0).
[Idea para una *demostración de la existencia de la función: Supongamos, por ejemplo, Fy(x0,y0)>0. Usando la continuidad Fy(x,y)>Fy(x0,y0)/2>0 para (x,y) cerca de (x0,y0) luego F(x0,y) es estrictamente creciente como función de y y para algún delta pequeño y F(x0,y−delta)<0<F(x0,y+delta). Por continuidad, F(x,y−delta)<0<F(x,y+delta) para (x,y) cerca de (x0,y0) y, fijo x, la ecuación F(x,y)=0 tiene solución única porque F(x,y) es estrictamente creciente como función de y ya que Fy(x,y)>>0.]
Geométricamente, este teorema establece que las soluciones de F(x,y)=0 (en color violeta en la figura) forman cerca de (x0,y0) una curva que coincide con la gráfica de la función y(x) (en azul en la figura).
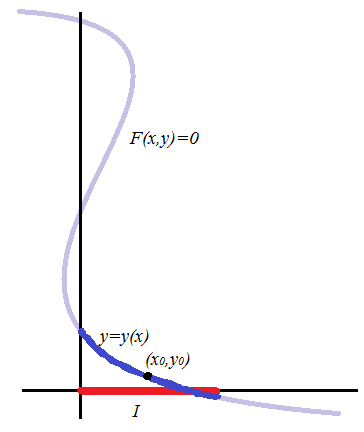
Interpretación geométrica del teorema de la función implícita.
Ecuación de la recta tangente a una curva dada por una ecuación implícita. La recta tangente a la gráfica de la curva y=y(x) en el punto A=(x0,y0) viene dada por y−y0=y′(x0)(x−x0), ecuación que, usando y′(x0)=−Fx(A)/Fy(A) e y(x0)=y0, podemos escribir como ∂F∂x(A)(x−x0)+∂F∂y(A)(y−y0)=0. Observemos en particular que, como ya sabíamos, ∇F(A) es un vector perpendicular a la curva definida por F(x,y)=0 en el punto A.
El papel de la incógnita que se despeja es intercambiable, o sea, se puede enunciar, lo que se deja como ejercicio, un teorema similar que nos da condiciones, la esencial es que ∂F∂x(x0,y0)≠0, que garantizan que podemos despejar x en función de y cerca de (x0,y0).
Puntos críticos. Los puntos donde ambas derivadas parciales se anulan se llaman puntos críticos y en ellos no podemos asegurar que la ecuación implícita represente una curva. Veremos en la siguiente lección que los puntos en los que un campo alcanza sus máximos y sus mínimos relativos son, precisamente, puntos críticos.
Procedimiento de derivación implícita.
Derivadas de orden superior de la función implícita. Una observación práctica importante es que si F admite derivadas parciales de orden superior, entonces, usando la regla de la cadena, podemos calcular derivadas de orden superior de y(x) para, por ejemplo, determinar los polinomios de Taylor de y centrados en x0, lo cual es muy útil si es imposible o muy complicado encontrar la fórmula y(x).
Para ello, una vez que ya sabemos que existe la función y(x) definida en el intervalo I que cumple y(x0)=y0 y F(x,y(x))=0 para todo x∈I, podemos derivar esta expresión con respecto a su variable independiente x usando la regla de la cadena, obteniendo (como vimos en la observación clave entes del teorema),
Fx(x,y(x))+Fy(x,y(x))⋅y′(x)=0,para todo x∈I.
Usando que para x=x0 tenemos y(x0)=y0 obtenemos el valor de y′(x0). Si volvemos a derivar con respecto a x la expresión anterior, tenemos
Fxx(x,y(x))+Fxy(x,y(x))⋅y′(x)+[Fxy(x,y(x))+Fyy(x,y(x))⋅y′(x)]⋅y′(x)+Fy(x,y(x))⋅y″(x)=0,para todo x∈I,
de donde podemos obtener y″(x0) poniendo x=x0 y usando los valores ya obtenidos y(x0)=y0 e y′(x0. Repitiendo este procedimiento, llamado derivación implícita, sucesivamente podríamos obtener las derivadas tercera, cuarta, …, de la función y(x) en el punto x0.
No hace falta recordar esta igualdad de memoria; la manera práctica de utilizar el procedimiento es ir derivando con respecto a x en la expresión dada F(x,y(x))=0 usando que y=y(x) es función de x como en el siguiente ejemplo.
Ejemplo. Si tomamos F(x,y)=x2+y2−1=0, como Fy(A)=1.6≠0, el teorema nos dice que cerca del punto A=(0.6,0.8) de la circunferencia x2+y2=1 podemos despejar la variable y como función y=y(x) de la variable x, de manera que x2+(y(x))2=1 para todo x en un intervalo I centrado en x0=0.6.
Esto ya lo sabíamos, por supuesto; de hecho, y(x)=√1−x2. Pero continuemos como si no supiéramos esto. Derivando x2+(y(x))2=1 con respecto a x, nos queda 2x+2y(x)y′(x)=0 para todo x∈I. Entonces, sustituyendo x=0.6 e y(0.6)=0.8, tenemos y′(0.6)=−0.6/0.8=−0.75. Con estos datos ya podemos escribir la ecuación de la recta tangente a la circunferencia: y=0.8−0.75(x−0.6).
Ahora, derivando implícitamente con respecto a x en 2x+2y(x)y′(x)=0, obtenemos 2+2(y′(x))2+2y(x)y″(x)=0 para todo x∈I, así que y″(0.6)=(−1−(y′(0.6))2)/y(0.6)=−1.95313. Con estos datos, obtenemos que el polinomio de Taylor de orden 2 de y(x) centrado en x0=0.6 viene dado por p2(x)=0.8−0.75(x−0.6)−0.9765563(x−0.6)2, sin que hayamos necesitado derivar dos veces la expresión √1−x2.
Ejercicios
Utiliza la aplicación Desmos, u otra similar, para dibujar las gráficas de las curvas que aparecen en los ejercicios.
Ejercicio 1. En los siguientes casos, aplica el teorema de la función implícita para hallar la ecuación de la recta tangente a la curva C, dada por una ecuación implícita, en el punto P.
- C dada por x3y2−3xy+2=0 en el punto P=(1,2).
- C dada por x3+y3=6xy en el punto P=(3,3).
- C dada por x2−3xy+2y3+cos(x)=π2−1 en el punto P=(π,0).
Ejercicio 2. La ecuación ay2+2bxy+cx2+αx+βy=0 define en el plano una cónica (quizás degenerada) que pasa por el origen. Halla la ecuación de la recta tangente a la cónica en ese punto.
Ejercicio 3. Prueba que la ecuación y3+a2y−2a3+axy−x3=0 define y como función implícita de x cerca del punto P=(0,a) y determina el polinomio de Taylor de orden 3 de dicha función (éste es el primer ejemplo usado por Newton en 1669). Haz lo mismo para el punto Q=(a,a).
Ejercicio 4. Prueba que sen(y)=x define implícitamente la variable y como función de la variable x alrededor de (0,0) y calcula su polinomio de Maclaurin de grado 3 (así obtuvo Newton el polinomio de Taylor de la función arcsen(x) en 1669). Haz lo mismo pero cerca del punto (0,π).
Ejercicio 5. Prueba que la ecuación y3+4y−x4+x=0 define implícitamente la variable y como función de la variable x en toda la recta real y halla su polinomio de Maclaurin de grado 2.
Ejercicio 6. Prueba que la ecuación y5+y−2x3+x=0 define implícitamente la variable y como función y(x) de la variable x cerca del origen y halla su el polinomio de Maclaurin de grado 3.
Ejercicio 7. Si usas un programa para dibujar la curva dada por x3−y3+2xy−x+y=0, verás que tiene dos ramas, una cerrada y otra abierta. La curva corta al eje OY en tres puntos (0,−1), (0,0) y (0,1), uno en la rama abierta y los otros dos en la cerrada. Prueba que cerca de cada uno de los puntos (0,−1), (0,0) y (0,1) se puede obtener la variable y como una función de x y calcula el polinomio de Maclaurin de grado 3 de cada una de dichas funciones.
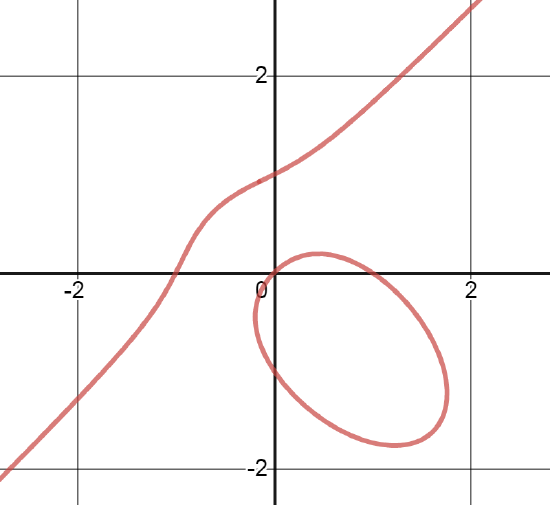
Ejercicio 8. Determina en qué puntos puedes aplicar el teorema de la función implícita a la ecuación x3axy+y3=0 para asegurar que define implícitamente una de las variables como función de la otra? ?`Qué pasa en el origen? La curva que se obtiene se llama folium de Descartes.
Ejercicio 9. La figura representa la isla en la que el pirata Morgan escondió el tesoro. Fijado un sistema de coordenadas cartesianas en el que las abscisas representan la longitud y las ordenadas la latitud, el contorno de la isla es la curva dada por x4−4x+4y2+y4=2

Para encontrar el tesoro debes dar los siguientes pasos:
- Halla el punto N más septentrional de la isla.
- Comprueba que en dicho punto la curva define la latitud y como función de la longitud x y halla el polinomio de Taylor de orden 2 de dicha función definida implícitamente.
- El tesoro está en el punto T de la isla en el que la gráfica de dicho polinomio corta al eje X.
- Dibuja la localización aproximada de los ejes coordenados, los puntos N y T y la gráfica del polinomio de Taylor mencionado.
*Ejercicio 10. El teorema de la función implícita no puede aplicarse en el origen de coordenadas a las siguientes ecuaciones porque en cada caso se tiene que es un punto crítico. ¿En qué casos es posible despejar una de las variables como una función de la otra cerca de dicho punto?
F1(x,y)=x2−y2=0,F2(x,y)=x2−y3=0,F3(x,y)=x3−y3=0.
*Ejercicio 11. La ecuación y−ϵsen(y)=m se llama ecuación de Kepler y relaciona varios parámetros importantes que caracterizan el movimiento orbital de un planeta. En esta ecuación, y es la anomalía excéntrica; ϵ, que es un número pequeño, es la excentricidad de la órbita elíptica; y m es la anomalía media.
- Suponiendo que ϵ está dado, utiliza el teorema de la función implícita para hallar el polinomio de Maclaurin de grado 3 de y=y(m) como función de m alrededor del punto (m=0,y=0).
- En otras ocasiones puede interesar, para un valor dado m, hallar y en función de ϵ. Utiliza el teorema de la función implícita en el punto (ϵ=0,y=m), para hallar el correspondiente polinomio de Maclaurin de grado 3 de y=y(ϵ).

