1.5: Cuadráticas
- Page ID
- 110550
Las cuadráticas son transformaciones de la función\( f(x)=x^2 \). Las cuadráticas suelen surgir de problemas relacionados con el movimiento de área y proyectil, proporcionando algunas aplicaciones interesantes.
Un granjero de patio trasero quiere encerrar un espacio rectangular para un nuevo jardín. Ella ha comprado 80 pies de cercado de alambre para encerrar tres lados, y pondrá el cuarto lado contra la barda del patio trasero. Encuentre una fórmula para el área encerrada por la barda si los lados del cercado perpendiculares a la barda existente tienen longitud\(L\).
Solución
En un escenario como este que involucra geometría, a menudo es útil dibujar un cuadro. También podría ser útil introducir una variable temporal,\(W\), para representar el lado del cercado paralelo al cuarto lado o cerca del patio trasero.
Ya que sabemos que solo tenemos 80 pies de barda disponibles, lo sabemos\( L+W+L=80 \), o más simplemente,\( 2L+W=80 \). Esto nos permite representar el ancho,\(W\), en términos de\(L\):\( W=80-2L \)
Ahora estamos listos para escribir una ecuación para el área que encierra la barda. Sabemos que el área de un rectángulo es longitud multiplicada por ancho, así\( A=LW=L(80-2l) \), entonces\[ A(L)=80L-2L^2. \nonumber \] Esta fórmula representa el área de la barda en términos de la longitud variable\(L\).
Actualmente un periódico local cuenta con 84 mil suscriptores, con un cargo trimestral de 30 dólares. Estudios de mercado han sugerido que si elevaban el precio a 32 dólares perderían 5 mil suscriptores. Suponiendo que las suscripciones están linealmente relacionadas con el precio, crear una ecuación para modelar sus ingresos en función del cargo trimestral.
Solución
Los ingresos son la cantidad de dinero que aporta una empresa. En este caso, los ingresos se pueden encontrar multiplicando el cargo por suscripción por el número de suscriptores. Podemos introducir variables,\(C\) para cargo por suscripción y\(S\) para el número de suscriptores, dándonos la ecuación:
Ingresos =\(C S\)
Dado que el número de suscriptores cambia con el precio, necesitamos encontrar una relación entre las variables.
Sabemos que actualmente\(S = 84,000\) y\(C = 30\), y que si suben el precio a 32 dólares perderían 5 mil suscriptores, dando un segundo par de valores,\(S = 79,000\) y\(C = 32\). A partir de esto podemos encontrar una ecuación lineal que relaciona las dos cantidades. Tratando\(C\) como la entrada y\(S\) como la salida, la ecuación tendrá forma\(S = mC + b\). La pendiente será
\[m = \dfrac{79,000 - 84,000}{32-30} = \dfrac{-5,000}{2} = -2,500\nonumber \]Esto nos dice que el periódico perderá 2,500 suscriptores por cada dólar que suban el precio. Entonces podemos resolver para la intercepción vertical.
\[S = -2500C + b\nonumber \]
Enchufe el punto\(S = 84,000\) y\(C = 30\)
\[84000 = -2500(30) + b\nonumber \]
Resolver para\(b\)
\[b = 159,000\nonumber \]
Esto nos da la ecuación lineal que\(S = -2,500C + 159,000\) relaciona costo y suscriptores. Tenga en cuenta que esta es una ecuación de demanda donde\(C\) está el precio y\(S\) es la cantidad demandada. Ahora volvemos a nuestra ecuación de ingresos.
Ingresos =\(C S\)
Sustituyendo la ecuación\(S\) de arriba:
Ingresos =\(C \left(-2,500C + 159,000\right)\)
Ampliación de
Ingresos =\(-2,500C^2 + 159,000C\)
Ahora tenemos una ecuación cuadrática para los ingresos en función del cargo por suscripción. Posteriormente en el curso utilizaremos ecuaciones como esta para determinar el precio a cobrar para maximizar los ingresos.
La forma estándar de una función cuadrática es\( f(x)=ax^2+bx+c \).
La forma de transformación de una función cuadrática es\( f(x)=a(x-h)^2+k \).
El vértice de la función cuadrática se localiza en\((h, k)\), donde\(h\) y\(k\) son los números en la forma de transformación de la función. Debido a que el vértice aparece en la forma de transformación, a menudo se le llama la forma de vértice.
Escriba una ecuación para la cuadrática graficada a continuación como una transformación de\( f(x)=x^2 \).
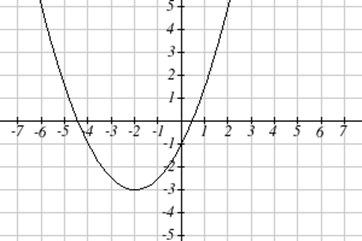
Solución
Podemos ver que la gráfica es la cuadrática básica desplazada hacia la izquierda 2 y hacia abajo 3, poniendo el vértice en\((-2, -3)\), dando una fórmula en la forma\( g(x)=a(x+2)^2-3 \). Al enchufar un punto que cae sobre la rejilla, como por ejemplo\((0,-1)\), podemos resolver para el factor de estiramiento:\[\begin{align*} -1 & = a(0+2)^2-3 \\ 2 & = 4a \\ a & = \frac{1}{2} \end{align*}\nonumber \]
La ecuación para esta fórmula es\[ g(x)=\frac{1}{2}(x+2)^2-3 \nonumber \]
Comportamiento a corto plazo: Intercepciones
Como con cualquier función, podemos encontrar las intercepciones verticales de una cuadrática evaluando la función en una entrada de cero, y podemos encontrar las intercepciones horizontales resolviendo para cuándo la salida será cero. Observe que dependiendo de la ubicación de la gráfica, podríamos tener cero, una o dos intercepciones horizontales.
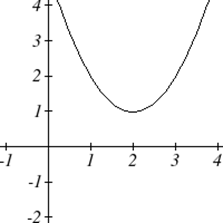
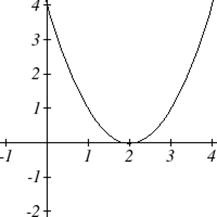
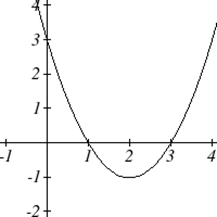
Observe que en la forma estándar de una cuadrática, el término constante\(c\) revela la intersección vertical de la gráfica, ya que\( f(0)=a(0)^2+b(0)+c=c \).
Encuentra las intercepciones verticales y horizontales de la cuadrática\( f(x)=3x^2+5x-2 \).
Solución
Podemos encontrar la intersección vertical evaluando la función en una entrada de cero:\[f(0)=3(0)^2+5(0)-2=-2\nonumber \] Entonces la intercepción vertical está en (0, -2)
Para las intercepciones horizontales, resolvemos para cuando la salida será cero:\[0=3x^2+5x-2.\nonumber \] En este caso, la cuadrática se puede factorizar fácilmente, proporcionando el método más simple para la solución.:\[0=(3x-1)(x+2),\nonumber \] entonces cualquiera\[ \begin{align*} 0 & = 3x-1\\ x & = \frac{1}{3} \end{align*} \nonumber \] o\[ \begin{align*} 0 & = x+2\\ x & = -2 \end{align*} \nonumber \] Así las intercepciones horizontales están en\( \left(\frac{1}{3},0\right) \) y\((-2,0)\).
Cuando una cuadrática no es factorizable o es difícil de factorizar, podemos recurrir a la fórmula cuadrática.
Para una función cuadrática dada en forma estándar\( f(x)=ax^2+bx+c \), la fórmula cuadrática da las intercepciones horizontales de la gráfica de esta función:\[ x=\frac{-b\pm \sqrt{b^2-4ac}}{2a} \nonumber \]
Se lanza una pelota hacia arriba desde lo alto de un edificio de 40 pies de altura a una velocidad de 80 pies por segundo. La altura de la pelota sobre el suelo puede ser modelada por la ecuación ¿\[ H(t)=-16t^2+80t+40 .\nonumber \]Cuándo golpea la pelota contra el suelo?
Solución
Para saber cuándo la pelota golpea el suelo, necesitamos determinar cuándo la altura es cero, es decir, cuándo\(H(t) = 0\). Si bien podríamos hacer esto usando la forma de transformación de la cuadrática, también podemos usar la fórmula cuadrática:\[ t=\frac{-80\pm \sqrt{80^2-4(-16)(40)}}{2(-16)}=\frac{-80\pm\sqrt{8960}}{-32} \nonumber \]
Como la raíz cuadrada no simplifica muy bien, podemos usar una calculadora para aproximar los valores de las soluciones:\[ t=\frac{-80-\sqrt{8960}}{-32}\approx 5.458 \quad\text{or}\quad t=\frac{-80+\sqrt{8960}}{-32}\approx -0.458 \nonumber \]
La segunda respuesta está fuera del dominio razonable de nuestro modelo, por lo que concluimos que la pelota golpeará el suelo después de aproximadamente 5.458 segundos.
La oferta de un determinado producto puede ser modelada por\(p = 3q^2\) y la demanda puede ser modelada por\(p = 1620 - 2q^2\), donde\(p\) está el precio en dólares, y\(q\) es la cantidad en miles de artículos. Encuentra el precio y la cantidad de equilibrio.
Solución
Recordemos que el equilibrio precio y cantidad se encuentra encontrando donde se cruzan la curva de oferta y demanda. Podemos encontrar que estableciendo las ecuaciones iguales:\[3q^2 = 1620 - 2q^2\nonumber\]
Añadir\(2q^2\) a ambos lados:\(5q^2 = 1620\)
Dividir por 5 en ambos lados:\(q^2 = 324\)
Tome la raíz cuadrada de ambos lados:\[q = \pm \sqrt{324} = \pm 18 \nonumber\]
Como no tiene sentido hablar de cantidades negativas, la cantidad de equilibrio es\(q = 18\). Para encontrar el precio de equilibrio, evaluamos cualquiera de las funciones en la cantidad de equilibrio. \[p = 3(18)^2 = 972\nonumber\]
El equilibrio es de 18 mil artículos, a un precio de $972.