2.2: Límites y Continuidad
- Page ID
- 110606
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Límite
En el último tramo, vimos que a medida que el intervalo sobre el que calculamos se hacía menor, las pendientes secantes se acercaban a la pendiente tangente. El límite nos da un mejor lenguaje con el que discutir la idea de “enfoques”.
El límite de una función describe el comportamiento de la función cuando la variable está cerca, pero no es igual, a un número especificado (ver la figura a continuación).
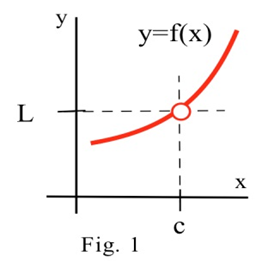
Si los valores de se\(f(x)\) acercan cada vez más, lo más cerca que queramos, a un número\(L\) ya que tomamos valores de\(x\) muy cerca (pero no igual a) un número\(c\), entonces decimos "el límite de\(f(x)\) como se\(x\) acerca\(c\) es\(L\)" y escribimos \[\lim\limits_{x\to c} f(x)=\mathbf{L}.\nonumber \]El símbolo "\( \to \)" significa “aproximaciones” o, menos formalmente, “se acerca mucho a”.
(Esta definición del límite no se afirma tan formalmente como podría ser, pero es suficiente para nuestros fines en este curso).
Nota:
- \(\bf f(c)\)es un solo número que describe el comportamiento (valor) de\(f(x)\) AT el punto\(x = c\).
- \(\lim\limits_{x\to c} f(x)\)es un solo número que describe el comportamiento de\(f(x)\) CERCA, PERO NO AT, el punto\(x = c\).
Si tenemos una gráfica de la función cerca\(x = c\), entonces suele ser fácil de determinar\( \lim\limits_{x\to c} f(x) \).
(Aquí hay un enlace a las imágenes utilizadas en el siguiente video así como en otras partes de este capítulo: Gráficas para Ejemplos de Límites y Continuidad.)
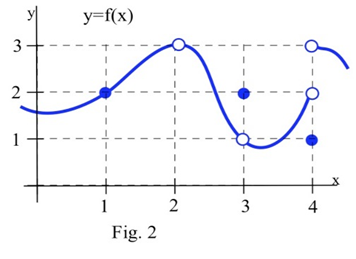
Utilice la gráfica de\(y = f(x)\) la siguiente figura para determinar los siguientes límites:
- \(\lim\limits_{x\to 1} f(x)\)
- \(\lim\limits_{x\to 2} f(x)\)
- \(\lim\limits_{x\to 3} f(x)\)
- \(\lim\limits_{x\to 4} f(x)\)
Solución
- \[\lim_{x \to 1} f(x) = 2\nonumber\]Cuando\(x\) está muy cerca de 1, los valores de\(f(x)\) están muy cerca de\(y = 2\). En este ejemplo, sucede eso\(f(1) = 2\), pero eso es irrelevante para el límite. Lo único que importa es lo que pase por\(x\) cerca de 1 pero\(x \neq 1\).
- \(f(2)\)es indefinido, pero solo nos importa el comportamiento de\(f(x)\) por\(x\) cerca de 2 pero no igual a 2. Cuando\(x\) está cerca de 2, los valores de\(f(x)\) son cercanos a 3. Si restringimos lo suficientemente\(x\) cerca a 2, los valores de\(y\) serán lo más cercanos a 3 como queramos, entonces\( \lim\limits_{x\to 2} f(x) = 3 \).
- Cuando\(x\) está cerca de 3 (o “como\(x\) se acerca al valor 3"), los valores de\(f(x)\) son cercanos a 1 (o “acercarse al valor 1"), entonces\( \lim\limits_{x\to 3} f(x) = 1 \). Para este límite es completamente irrelevante que\(f(3) = 2\), solo nos importa lo que pase a\(f(x)\) por\(x\) cerca y no igual a 3.
- Este es más difícil y hay que tener cuidado. Cuando\(x\) está cerca de 4 y un poco menos de 4 (\(x\)está justo a la izquierda de 4 en el\(x\) eje -), entonces los valores de\(f(x)\) son cercanos a 2. Pero si\(x\) está cerca de 4 y ligeramente mayor que 4 entonces los valores de\(f(x)\) son cercanos a 3. Si sólo sabemos que\(x\) está muy cerca de 4, entonces no podemos decir si\(y = f(x)\) va a estar cerca de 2 o cerca de 3 —depende de si\(x\) está en el lado derecho o izquierdo de 4. En esta situación, los\(f(x)\) valores no se acercan a un solo número por lo que decimos que\(\lim\limits_{x\to 4} f(x)\) no existe. Eso es irrelevante\(f(4) = 1\). El límite, a medida que\(x\) se acerca a 4, seguiría siendo indefinido si\(f(4)\) fuera 3 o 2 o cualquier otra cosa.
También podemos explorar límites usando tablas y usando álgebra.
Encuentra\( \lim\limits_{x\to 1} \dfrac{2x^2-x-1}{x-1} \).
Solución
Podrías intentar evaluar\(f(x) = \frac{2x^2-x-1}{x-1}\) en\(x = 1\), pero no\(f(x)\) se define en\(x = 1\). Es tentador, pero erróneo, concluir que esta función no tiene límite a medida que se\(x\) acerca 1.
Usando tablas: Probando algunos valores de “prueba” para los\(x\) cuales se acercan cada vez más a 1 tanto de la izquierda como de la derecha, obtenemos
| \( x \) | \( f(x) \) |
|---|---|
| \ (x\) ">0.9 | \ (f (x)\) ">2.82 |
| \ (x\) ">0.9998 | \ (f (x)\) ">2.9996 |
| \ (x\) ">0.999994 | \ (f (x)\) ">2.999988 |
| \ (x\) ">0.9999999 | \ (f (x)\) ">2.9999998 |
| \ (x\) ">\( \to 1 \) | \ (f (x)\) ">\( \to 3 \) |
| \( x \) | \( f(x) \) |
|---|---|
| \ (x\) ">1.1 | \ (f (x)\) ">3.2 |
| \ (x\) ">1.003 | \ (f (x)\) ">3.006 |
| \ (x\) ">1.0001 | \ (f (x)\) ">3.0002 |
| \ (x\) ">1.000007 | \ (f (x)\) ">3.000014 |
| \ (x\) ">\( \to 1 \) | \ (f (x)\) ">\( \to 3 \) |
La función no\(f\) está definida en\(x = 1\), pero cuando\(x\) está cerca de 1, los valores de\(f(x)\) se están acercando mucho a 3. Podemos llegar\(f(x)\) lo más cerca de 3 como queramos tomando\(x\) muy cerca de 1 así\[\lim\limits_{x\to 1} \dfrac{2x^2-x-1}{x-1}=3.\nonumber \]
Usando álgebra: Podríamos haber encontrado el mismo resultado al señalar que\[ f(x)= \dfrac{2x^2-x-1}{x-1} = \dfrac{(2x+1)(x-1)}{(x-1)} = 2x+1\nonumber \] mientras\(x \neq 1\). (Si\(x\neq 1\), entonces\(x–1 \neq 0\) así es válido dividir el numerador y denominador por el factor\(x–1\).) La parte\(x\to 1\) "" del límite significa que\(x\) está cerca de 1 pero no igual a 1, por lo que nuestro paso de división es válido y\[ \lim\limits_{x\to 1}\dfrac{2x^2-x-1}{x-1} = \lim\limits_{x\to 1} 2x+1 = 3,\nonumber \] cual es nuestra respuesta.
Usando una gráfica: Podemos graficar\( y=f(x)= \dfrac{2x^2-x-1}{x-1} \) para\(x\) cerca de 1:
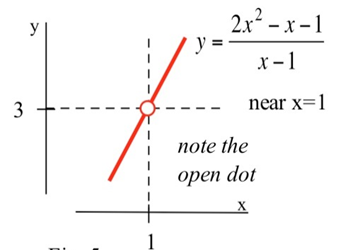
Observe que siempre que\(x\) esté cerca de 1, los valores de\(y = f(x)\) son cercanos a 3. Ya que no\(f\) se define en\(x = 1\), la gráfica tiene un agujero arriba\(x = 1\), pero solo nos importa lo que\(f(x)\) está haciendo para\(x\) cerca pero no igual a 1.
Encuentra\(\lim \limits_{x\to 3} \dfrac{\frac{1}{x} -\frac{1}{3} }{x-3}\).
Solución
Observe que esta función no está definida en\(x = 3\). Podemos encontrar el límite usando álgebra. Dando a los dos términos en el numerador un denominador común, podemos simplificar:
\[ \frac{\frac{1}{x} -\frac{1}{3} }{x-3} = \frac{\frac{1}{x} \cdot \frac{3}{3} -\frac{1}{3} \cdot \frac{x}{x} }{x-3} = \frac{\frac{3}{3x} -\frac{x}{3x} }{x-3} =\frac{\frac{3-x}{3x} }{x-3} \nonumber \]
Recuerda que dividir una fracción es lo mismo que multiplicar por lo recíproco, por lo que
\[\frac{\frac{3-x}{3x} }{x-3} =\frac{\frac{3-x}{3x} }{\frac{x-3}{1} }\nonumber \] equivale a\[\frac{3-x}{3x} \cdot \frac{1}{x-3}\nonumber \]
Para simplificar aún más, necesitamos factorial un 1 negativo del numerador. Entonces podremos cancelar el plazo\(\left(x-3\right)\)
\(\dfrac{-1(x-3)}{3x} \cdot \dfrac{1}{x-3} =\dfrac{-1}{3x}\) siempre y cuando\(x \neq 3\)
Ahora podemos evaluar el límite usando esta forma simplificada.
\[\lim\limits_{x\to 3} \frac{\frac{1}{x} -\frac{1}{3} }{x-3} = \lim\limits_{x\to 3} \frac{-1}{3x} = -\frac{1}{9} \nonumber \]
Límites de un solo lado
En ocasiones, lo que nos sucede en un lugar depende de la dirección que usemos para acercarnos a ese lugar. Si nos acercamos a las Cataratas del Niágara desde el lado aguas arriba, entonces estaremos 182 pies más altos y tendremos diferentes preocupaciones que si nos acercamos desde el lado aguas abajo. Del mismo modo, los valores de una función cerca de un punto pueden depender de la dirección que usemos para acercarnos a ese punto.
El límite izquierdo de\(f(x)\) como\(c\) se\(x\) acerca es\(L\) si los valores de\(f(x)\) get tan cerca\(L\) como queremos cuando\(x\) está muy cerca y a la izquierda de\(c\) (i.e.,\(x \lt \mathbf{c}\)). Escribimos\[\lim\limits_{x\to c^-} f(x)=L.\nonumber \]
El límite correcto de\(f(x)\) como\(x\) enfoques\(c\), escrito con\(\bf x \to c^+\), es\(L\) si los valores de\(f(x)\) llegar tan cerca\(L\) como queremos cuando\(x\) está muy cerca y derecha de\(c\) (es decir,\(x \gt \mathbf{c}\)). Escribimos\[\lim\limits_{x\to c^+} f(x)=L.\nonumber \]
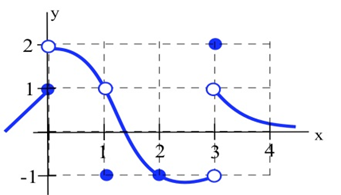
Evalúe los límites unilaterales de la función\(f(x)\) graficada a continuación en\(x = 0\) y\(x = 1\).
Solución
A medida que se\(x\) aproxima 0 desde la izquierda, el valor de la función se está acercando a 1, por lo que\( \lim\limits_{x\to 0^-} f(x) = 1. \)
A medida que\(x\) se acerca a 0 desde la derecha, el valor de la función se acerca a 2, por lo que\( \lim\limits_{x\to 0^+} f(x) = 2. \)
Observe que dado que el límite de la izquierda y el límite de la derecha son diferentes, el límite general\( \lim\limits_{x\to 0} f(x) \),, no sale.
En\(x\) los enfoques 1 desde cualquier dirección, el valor de la función se acerca a 1, entonces\[\lim\limits_{x\to 1^-} f(x) = \lim\limits_{x\to 1^+} f(x) = \lim\limits_{x\to 1} f(x) = 1. \nonumber \]
Continuidad
Una función que es “amigable” y que no tiene ningún break o saltos en ella se llama continua. De manera más formal,
Una función\(\bf f\) es continua en\(\bf x = a \) si y solo si\( \lim\limits_{x\to a} \mathbf{f(x)} = \mathbf{f(a)}\).
El siguiente gráfico ilustra algunas de las diferentes formas en que una función puede comportarse en y cerca de un punto, y la tabla contiene cierta información numérica sobre la función y su comportamiento.
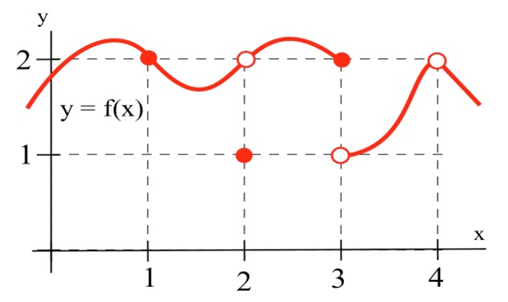
| \( a \) | \( f(a) \) | \( \lim\limits_{x\to a} f(x) \) |
| 1 | 2 | 2 |
| 2 | 1 | 2 |
| 3 | 2 | No existe (DNE) |
| 4 | Sin definir | 2 |
Con base en la información de la tabla, podemos concluir que\(f\) es continuo a 1 ya que\( \lim\limits_{x\to 1} f(x) = 2 = f(1)\).
También podemos concluir a partir de la información en la tabla que no\(f\) es continua a 2 o 3 o 4, porque\( \lim\limits_{x\to 2} f(x) \neq f(2) \),\( \lim\limits_{x\to 3} f(x) \neq f(3) \), y\( \lim\limits_{x\to 4} f(x) \neq f(4) \).
Los comportamientos en\(x = 2\) y\(x = 4\) exhiben un agujero en la gráfica, a veces llamado discontinuidad removible, ya que la gráfica podría hacerse continua cambiando el valor de un solo punto. El comportamiento at\( x = 3 \) se denomina discontinuidad de salto, ya que la gráfica salta entre dos valores.
Entonces, ¿qué funciones son continuas? Resulta que prácticamente todas las funciones que has estudiado son continuas donde se define: las funciones polinomiales, radicales, racionales, exponenciales y logarítmicas son todas continuas donde se definen. Además, cualquier combinación de funciones continuas también es continua.
Esto es útil, porque la definición de continuidad dice que para una función continua,\( \lim\limits_{x\to a} f(x) = f(a) \). Eso significa que para una función continua, podemos encontrar el límite por sustitución directa (evaluando la función) si la función es continua en\(a\).
Evaluar usando continuidad, si es posible:
- \( \lim\limits_{x\to 2} x^3-4x \)
- \( \lim\limits_{x\to 2} \dfrac{x-4}{x+3} \)
- \( \lim\limits_{x\to 2} \dfrac{x-4}{x-2} \)
Solución
- La función dada es polinomio, y se define para todos los valores de\(x\), por lo que podemos encontrar el límite por sustitución directa:\[ \lim\limits_{x\to 2} x^3-4x = 2^3-4(2) = 0. \nonumber \]
- La función dada es racional. No se define en\(x = -3\), pero estamos tomando el límite como se\(x\) acerca a 2, y la función se define en ese punto, por lo que podemos usar la sustitución directa:\[ \lim\limits_{x\to 2} \dfrac{x-4}{x+3} = \dfrac{2-4}{2+3}= -\dfrac{2}{5}. \nonumber \]
- Esta función no se define en\(x = 2\), y por lo tanto no es continua en\(x = 2\). No podemos usar la sustitución directa.