3.4: Antiderivados de Fórmulas
- Page ID
- 110510
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ahora podemos juntar las ideas de áreas y antiderivados para obtener una forma de evaluar integrales definidas que sea exacta y muchas veces fácil. Para evaluar una integral definida\( \int\limits_a^b f(t)\, dt \), podemos encontrar cualquier antiderivado\(F(t)\) de\(f(t)\) y evaluar\(F(b) - F(a)\). El problema de encontrar el valor exacto de una integral definida se reduce a encontrar alguna (cualquier) antiderivada\(F\) del integrando y luego evaluando\(F(b) - F(a)\). Incluso encontrar un antiderivado puede ser difícil, y nos apegaremos a funciones que tengan antiderivados fáciles.
Bloques de construcción
La antidiferenciación está retrocediendo a través del proceso derivado. Entonces, las reglas antiderivadas más fáciles son simplemente versiones al revés de las reglas derivadas más fáciles. Recordar del Capítulo 2:
En lo que sigue,\(f\) y\(g\) son funciones diferenciables de\(x\).
Regla múltiple constante
\[ \frac{d}{dx}\left( kf\right)=kf'\nonumber \]
Regla de suma y diferencia
\[\frac{d}{dx}\left(f\pm g\right)=f' \pm g'\nonumber \]
Regla de Poder
\[\frac{d}{dx}\left(x^n\right)=nx^{n-1}\nonumber \]
Casos especiales:\[\frac{d}{dx}\left(k\right)=0 \quad \text{(Because \( k=kx^0 \).)}\nonumber \]\[\frac{d}{dx}\left(x\right)=1 \quad \text{(Because \( x=x^1 \).)}\nonumber \]
Funciones exponenciales
\[\frac{d}{dx}\left(e^x\right)=e^x\nonumber \]\[\frac{d}{dx}\left(a^x\right)=\ln(a)\,a^x\nonumber \]
Logaritmo natural
\[\frac{d}{dx}\left(\ln(x)\right)=\frac{1}{x}\nonumber \]
Pensar en estas reglas básicas fue cómo se nos ocurrieron los antiderivados de\(2x\) y\( e^x \) antes.
Las reglas correspondientes para los antiderivados son las siguientes: cada una de las reglas antiderivadas es simplemente reescribir la regla derivada. Todos estos antiderivados se pueden verificar diferenciando.
Hay una sorpresa — el antiderivado de en realidad no\(\frac{1}{x}\) es simplemente\(\ln(x)\), es\(\ln|x|\). Esto es algo bueno —el antiderivado tiene un dominio que coincide con el dominio de\(\frac{1}{x}\), que es más grande que el dominio de\(\ln(x)\), así que no tenemos que preocuparnos\(x\) de si los nuestros son positivos o negativos. Pero debemos tener cuidado de incluir esos valores absolutos —de lo contrario, podríamos terminar con problemas de dominio.
En lo que sigue,\(f\) y\(g\) son funciones diferenciables de\(x\), y\( k \)\( n \),, y\( C \) son constantes.
Regla múltiple constante
\[ \int k\cdot f(x)\, dx=k\cdot\int f(x)\, dx\nonumber \]
Regla de suma y diferencia
\[\int \left(f(x)\pm g(x)\right)\, dx=\int f(x)\, dx \pm \int g(x)\, dx\nonumber \]
Regla de Poder
\[ \int x^n \, dx = \frac{x^{n+1}}{n+1}+C, \text{ provided that } n\neq -1\nonumber \]
Caso especial:\[ \int k\, dx =kx+C \quad \text{(Because \( k=kx^0 \).)}\nonumber \] (El otro caso especial (\( n=-1 \)) se cubre a continuación.)
Logaritmo natural
\[\int x^{-1}\, dx =\int\frac{1}{x}\, dx = \ln|x|+C\nonumber \]
Funciones exponenciales
\[ \int e^x\, dx=e^x +C \nonumber \]\[ \int a^x\, dx = \frac{a^x}{\ln(a)}+C \nonumber \]
Encuentra el antiderivado de\( y=3x^7-15\sqrt{x}+\frac{14}{x^2} \).
Solución
\[ \begin{align*} \int\left( 3x^7-15\sqrt{x}+\frac{14}{x^2} \right)\, dx & = \int\left( 3x^7-15x^{1/2}+14x^{-2} \right)\, dx \\ & = 3\frac{x^8}{8}-15\frac{x^{3/2}}{3/2}+14\frac{x^{-1}}{-1}+C \\ & = \frac{3}{8}x^8-10x^{3/2}-14x^{-1}+C \end{align*} \nonumber \]
Encontrar\( \int\left(e^x+12-\frac{16}{x}\right)\, dx \).
Solución
\[ \int\left(e^x+12-\frac{16}{x}\right)\, dx =e^x+12x-16\ln|x|+C\nonumber \]
Encuentra\(F(x)\) para que\( F'(x)=e^x \) y\( F(0)=10 \).
Solución
Esta vez estamos buscando un antiderivado particular; necesitamos encontrar exactamente la constante correcta. Empecemos por encontrar el antiderivado:\[ \int e^x\, dx=e^x+C \nonumber \]
Entonces lo sabemos\( F(x)=e^x+\text{(some constant)} \), ahora solo necesitamos encontrar cuál. Para ello, usaremos el otro dato (la condición inicial):\[ \begin{align*} F(x) & = e^x+C \\ F(0) & = e^0+C=1+C=10 \\ C & = 9 \end{align*} \nonumber \]
La constante particular que necesitamos es 9; así,\( F(x)=e^x+9 \).
La razón por la que estamos viendo los antiderivados en este momento es para que podamos evaluar integrales definidas exactamente. Recordemos el Teorema Fundamental del Cálculo:
Si\(F(x)\) es una función donde\(F'(x) = f(x)\), entonces
\[ \int\limits_a^b f(x)\, dx = F(b)-F(a) \nonumber \]
Si podemos encontrar un antiderivado para el integrando, podemos usarlo para evaluar la integral definida. La evaluación\(F(b) - F(a)\) se representa como\( \left.F(x)\right]_a^b \) o\( \left.F(x)\right|_a^b \).
Evaluar\( \int\limits_1^3 x\, dx \) de dos maneras:
- Dibujando la gráfica\(y = x\) y encontrando geométricamente el área.
- Al encontrar un antiderivado\(F(x)\) del integrando y evaluando\(F(3)-F(1)\).
Solución
- A continuación\(y = x \) se muestra la gráfica de, y la región sombreada correspondiente a la integral tiene área 4.
- Uno antiderivado de\(x\) es\( F(x)=\frac{1}{2}x^2 \), y\[ \begin{align*} \int\limits_1^3 x\, dx & = \left[\frac{1}{2}x^2\right]_1^3 \\ & = \left(\frac{1}{2}(3)^2\right) - \left(\frac{1}{2}(1)^2\right) \\ & = \frac{9}{2}-\frac{1}{2} \\ & = 4. \end{align*} \nonumber \] Tenga en cuenta que esta respuesta concuerda con la respuesta que obtuvimos geométricamente.
Si hubiéramos usado otro antiderivado de x, digamos\( F(x)=\frac{1}{2}x^2+7 \), entonces\[ \begin{align*} \int\limits_1^3 x\, dx & = \left[\frac{1}{2}x^2+7\right]_1^3 \\ & = \left(\frac{1}{2}(3)^2+7\right) - \left(\frac{1}{2}(1)^2+7\right) \\ & = \frac{9}{2}+7-\frac{1}{2}-7 \\ & = 4. \end{align*} \nonumber \]
En general, cualquier constante que escojamos se resta durante la evaluación, por lo que bien podríamos elegir siempre la más fácil, donde la constante es 0.
Encuentra el área entre la gráfica de\(y = 3x^2\) y el eje horizontal para\(x\) entre 1 y 2.
Solución
Esto es\[ \int\limits_1^2 3x^2\, dx = \left.x^3\right|_1^2 = 2^3-1^3 = 7. \nonumber \]
Se ha programado un robot para que cuando empiece a moverse, su velocidad después de\(t\) segundos sea\( 3t^2 \) pies/segundo.
- ¿Hasta dónde viajará el robot durante sus primeros 4 segundos de movimiento?
- ¿Hasta dónde viajará el robot durante sus próximos 4 segundos de movimiento?
Solución
- La distancia durante los primeros 4 segundos será el área bajo la gráfica de velocidad, de\(t = 0\) a\(t = 4\).
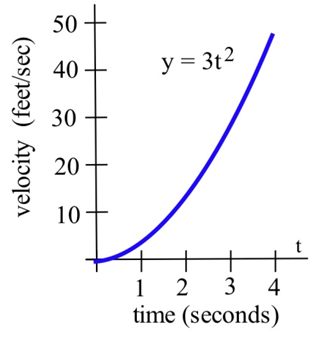
Esa área es la integral definitiva\( \int\limits_0^4 3t^2\, dt \). Un antiderivado de\( 3t^2 \) es\( t^3 \), así\( \int\limits_0^4 3t^2\, dt =\left. t^3 \right]_0^4 =4^3-0^3 = 64\) pies.
- \( \int\limits_4^8 3t^2\, dt =\left. t^3 \right]_4^8=8^3-4^3 =512 - 64 = 448\)pies.
Supongamos que\(t\) minutos después de poner 1000 bacterias en una placa de Petri la tasa de crecimiento de la población es de\(6t\) bacterias por minuto.
- ¿Cuántas bacterias nuevas se agregan a la población durante los primeros 7 minutos?
- ¿Cuál es la población total después de 7 minutos?
Solución
- El número de bacterias nuevas es el área bajo la gráfica de tasa de crecimiento, y una antiderivada de\(6t\) es\(3t^2\).
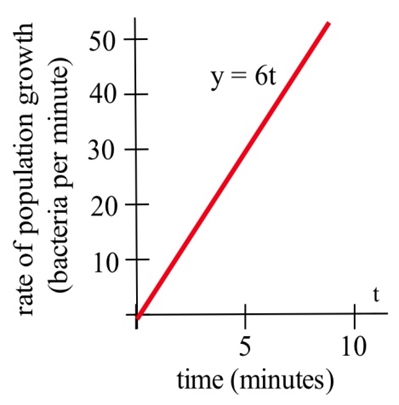
Entonces\[\text{new bacteria}=\int\limits_0^7 6t\, dt= \left. 3t^2\right|_0^7=3(7)^2-3(0)^2=147\nonumber \]
- La nueva población = (población antigua) + (nueva bacteria) = 1000 + 147 = 1147 bacterias.
Una empresa determina su costo marginal de producción, en dólares por artículo, es\( MC(x)=\frac{4}{\sqrt{x}}+2 \) al producir\(x\) mil artículos. Encuentra el costo de incrementar la producción de 4 mil artículos a 5 mil artículos.
Solución
Recordemos que el costo marginal es la tasa de cambio de costo, y así lo dice el teorema fundamental\( \int\limits_a^b MC(x)\, dx = \int\limits_a^b C'(x)\, dx = C(b)-C(a) \). Es decir, la integral del costo marginal nos dará un cambio neto en el costo. Para encontrar el costo de incrementar la producción de 4 mil artículos a 5 mil artículos, necesitamos integrar\( \int\limits_4^5 MC(x)\, dx\).
Podemos escribir el costo marginal como\( MC(x)=4x^{-1/2}+2 \). Entonces podemos usar las reglas básicas para encontrar un antiderivado:\[ C(x)=4\frac{x^{1/2}}{1/2}+2x=8\sqrt{x}+2x.\nonumber \]
Usando esto,\[ \begin{align*} \text{Net change in cost } & = \int\limits_4^5 \left(4x^{-1/2}+2\right)\, dx \\ & = \left[ 8\sqrt{x}+2x \right]_4^5 \\ & = \left( 8\sqrt{5}+2(5) \right)-\left( 8\sqrt{4}+2(4) \right) \\ & \approx 3.889 \end{align*} \nonumber \]
Costará 3.889 mil dólares incrementar la producción de 4 mil artículos a 5 mil artículos. (La respuesta final se escribiría mejor como 3889 dólares.)


