1.2: El conjunto R
( \newcommand{\kernel}{\mathrm{null}\,}\)
¿Qué son exactamente los números reales? Sabemos que 5,−8/5,√2,π, e, … lo son, que los tres últimos no son racionales y no se pueden expresar sin utilizar infinitos decimales, que no se pueden escribir como una fracción. Se saben resolver algunas ecuaciones con coeficientes reales, trabajar con desigualdades... Se podría trabajar sólo con esta idea intuitiva, pero en matemáticas a veces la intuición engaña. Convendría tener una definición rigurosa del conjunto R de los números reales. Lo mas serio (pero muy largo) sería construir los reales a partir de los racionales. Para ahorrar tiempo, definiremos R como un conjunto de objetos básicos que satisfacen unas propiedades dadas que tomaremos como axiomas (si se construyese R estas propiedades serían teoremas que habría que demostrar). De ellas se podrían deducir el resto de propiedades que nos permiten hacer cálculos con reales (tampoco lo haremos (seguiría siendo demasiado largo), pero es interesante leer el Spivak para ver como se hace). Así pues, definimos a partir de las propiedades vistas para Q :
Axiomas del conjunto
R & R es un conjunto que posee las propiedades 1),…,6) de cuerpo ordenado y además satisface el axioma del extremo superior
El último axioma (que vemos algo más adelante, pues exige alguna definición) distingue R de Q
Gracias al orden que hay en R tiene sentido la representación usual de R como una línea recta,  asociando a cada número real un punto de la recta. Es tan común que se utilizan indistintamente los términos 'conjunto de números reales' y 'recta real'; 'número real' y 'punto'.
asociando a cada número real un punto de la recta. Es tan común que se utilizan indistintamente los términos 'conjunto de números reales' y 'recta real'; 'número real' y 'punto'.
A partir exclusivamente de los axiomas se podrían demostrar todo el resto de propiedades de los números reales que se habrán utilizado en cursos anteriores. Repasamos sin demostrarlas algunas referentes a desigualdades, porque suele haber problemas en el trabajo con ellas:
Teorema:
| a<b⇒a+c<b+c,a−c<b−c | a<b,c<d⇒a+c<b+d,a−d<b−c |
| a<b,c>0⇒ac<bc,a/c<b/c | a<b,c<d⇒ac<bd, si a,b,c,d>0 |
| a<b,c<0⇒ac>bc,a/c>b/c | a/c<b/d⇔ad<bc, si a,b,c,d>0 |
| 1<a⇒a<a2;0<a<1⇒a>a2 | a<b⇔1/a>1/b,a2<b2,√a<√b, si a,b>0 |
Todas las desigualdades son válidas sustituyendo los < por ≤(menoslos>0 ó <0).
[En estos apuntes (y como siempre se hace) √a representará siempre sólo la raíz positiva del número a≥0; el otro número real cuyo cuadrado es ese número a se debe representar por −√a].
Ej. Determinemos todos los reales x que satisfacen: x2+2x>3
Si x=0, el cociente no está definido. Si x≠0, como es lícito sumar o restar a ambos lados, la desigualdad equivale a: x2+2x−3=x3−3x+2x>0. El cociente será positivo si y sólo tienen el mismo signo denominador y numerador. Para conocer el signo de éste necesitamos hallar sus raíces. Aunque esto es complicado en general, es claro aquí que x=1 lo anula, y así, dividiendo por (x−1), tenemos que x3−3x+2=(x−1)(x2+x−2)=(x−1)2(x+2). Como el numerador es estrictamente positivo si x>−2,x≠1 y negativo si x<−2, los x buscados son:

{x:x<−2 ó 0<x<1 ó x>1}
Podríamos haber operado de otra forma, multiplicando ambos miembros por x, pero teniendo siempre cuidado con que al multiplicar por números negativos las desigualdades se invierten.
Si x>0, la desigualdad equivale a x3−3x+2=(x−1)2(x+2)>0→ todo x>0 con x≠1.
Si x<0, cambia la desigualdad: x3−3x+2=(x−1)2(x+2)<0→ todo x<−2.
A cada x∈R podemos asociar un real positivo |x|, valor absoluto de x, definido por:
|x|=√x2={x si x≥0−x si x≤0
|x| representa la distancia de x al origen y|x−y| la distancia de x a y (tanto si y>x como si x>y )
Propiedades inmediatas a partir de la definición son:
|x|2=x2,|x|=|−x|,|xy|=|x||y|,−|x|≤x≤|x|
Probemos otras que utilizaremos en muchas ocasiones:
Teorema: Sea a>0:|x|≤a⇔−a≤x≤a;|x|<a⇔−a<x<a
⇐) sea −a≤x≤a; si x3≥0,|x|=x≤a; si x≤0,|x|=−x≤a; por tanto, ∀x,|x|≤a 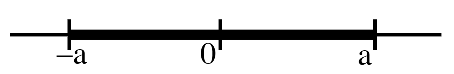
[con el < se demostraría igual; del teorema se deduce, desde luego, que
|x|≥a⇔x≤−a ó a≤x, puesto que la afirmación ' p⇔q ' equivale a la '(no p)⇔( no q)']
\[
\begin{aligned}
& \text { Teorema: }\left[|x+y|≤|x|+|y|( desigualdad triangular); |x|−|y|≤|x−y|≤|x|+|y|;||x|−|y||≤|x−y|\right. \\
& (|x+y|)^{2}=(x+y)^{2}=x^{2}+2 x y+y^{2} \leq|x|^{2}+2|x||y|+|y|^{2}=(|x|+|y|)^{2} \Rightarrow|x+y| \leq|x|+|y| \\
& |x|=|x-y+y| \leq|x-y|+|y| \Rightarrow|x|-|y| \leq|x-y| ;|x-y|=|x+(-y)| \leq|x|+|-y|=|x|+|y| \\
& |x|-|y| \leq|x-y| ;|y|-|x| \leq|x-y| \Rightarrow|x|-|y| \geq-|x-y| \Rightarrow|| x|-| y|| \leq|x-y|
\end{aligned}
\]
Ej. Determinemos losx que satisfacen: |√x−2|=x
Si x<0, la raíz no está definida. Desarrollando (para x≥0 ) el valor absoluto tenemos:
|√x−2|={√x−2 si √x≥2, es decir, si x≥42−√x si √x≤2, es decir, si 0≤x≤4Y, por tanto, |√x−2|=x⇔{√x=x+2 si x≥4⇒x2+3x+4=0√x=2−x si 0≤x≤4⇒x2−5x+4=0
El primer polinomio de segundo grado no se anula para ningún x real. El segundo para x=1 y para x=4 (ambos en la región 0≤x≤4 en que estamos). Pero sólo es válido x=1 (|1−2|=1 ). El otro real x=4 no cumple la igualdad: |2−2|≠4 (nos lo hemos inventado al elevar al cuadrado).
Ej. Hallemos los x que cumplen: |x2−1|≤3⇔−3≤x2−1≤3⇔−2≤x2≤4.
Ambas desigualdades se cumplen si y sólo si |x|≤2(⇔x2≤4; la primera es cierta ∀x ). Podemos llegar a lo mismo discutiendo las posibilidades del valor absoluto (más largo): 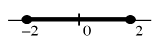
3≥|x2−1|={x2−1 si |x|≥11−x2 si |x|≤1⇔{x2≤4 si |x|≥1→1≤|x|≤2x2≥−2 si |x|≤1→ todo |x|≤1
Ej. Probemos ahora que para todo x se cumple −8≤|x−5|−|x+3|≤8.
Los teoremas aseguran: |x|−5≤|x−5|≤|x|+5,|x|−3≤|x+3|≤|x|+3. Por tanto:
|x−5|−|x+3|≤|x|+5−[|x|−3]=8 (mayor-menor) y|x−5|−|x+3|≥|x|−5−[|x|+3]=−8 (menor-mayor)
También lo podríamos haber hecho expresando los valores absolutos según los valores de x.
Para enunciar el axioma del extremo superior necesitamos unas definiciones previas:
Un conjunto A⊂R se dice acotado superiormente (inferiormente) si existe k∈R tal que a≤k(a≥k) para todo a∈A. A un real k con esa propiedad se le llama cota superior (inferior) de A.A se dice acotado si lo está superior e inferiormente ( ⇔∃k tal que |a|≤k,∀a∈A).
Ej.R+={x:x≥0} no es acotado, aunque sí lo está inferiormente (por −π, por el propio 0…. .
\includegraphics[max width=\textwidth]{2022_05_28_c7df107b7d10f7110aceg-016(1)}
[cotas superiores: √93,7 (la menor), .. ; cotas inferiores: −13,0 (la mayor), ..] .
\includegraphics[max width=\textwidth]{2022_05_28_c7df107b7d10f7110aceg-016(2)}
[cotas superiores: π,1 (la menor), …; cotas inferiores: −3,0 (la mayor), . ].
Extremo superior (o supremo) de A es la menor de sus cotas superiores. Es decir:
s∈R es el extremo superior o supremo deA[supA] si:
i) s es cota superior de A, ii) si k es cota superior de A entonces s≤k.
[Se define análogo extremo inferior o ínfimo de A [ infA ], mayor de las cotas inferiores].
El supA puede pertenecer o no a A; si pertenece se le llama máximo, es decir:
M∈R es el máximo de A[maxA] si M∈A y a≤M,∀a∈A (análogamente, min A )
Ej. Z, sin cotas superiores ni inferiores, no puede tener ni supremo ni ínfimo. 7 es el supremo del A de antes (es la cota superior más pequeña), pero no es máximo, pues 7∉A;0 es su mínimo (y, por tanto, su ínfimo). Para B,1 es el máximo (y supremo) y 0 el ínfimo (no mínimo).
\subsection{El conjunto R}
Axioma del Todo conjunto no vacío de números reales acotado extremo superior: superiormente posee extremo superior.
[no es difícil demostrar que la afirmación: 'todo conjunto no vacío de números reales acotado inferiormente posee extremo inferior' es equivalente al axioma]
Este axioma precisa la idea intuitiva de que los números reales 'llenan del todo' la recta real. Como ocurría en Q, entre todo par de reales distintos existen infinitos reales
\includegraphics[max width=\textwidth]{2022_05_28_c7df107b7d10f7110aceg-017}\\
(infinitos racionales e infinitos irracionales). Pero a pesar de estar también los elementos de Q 'tan cerca unos de otro como queramos', dejan sin embargo 'huecos' entre ellos (los puntos ocupados por los infinitos irracionales). Por eso hay conjuntos acotados en Qsin supremo. Por ejemplo, {x∈Q:x2<2} es un subconjunto de Q con cotas superiores racionales (3/2 , por ejemplo) pero no existe ninguna en Q que sea la más pequeña. Dada cualquier cota racional siempre puedo encontrar otra menor (más cercana al irracional √2). El mismo conjunto, visto como subconjunto de R debe tener supremo: √2 lo es.
Los siguientes subconjuntos de R van a aparecer un montón de veces en estos apuntes:
Intervalos. Dados a<b se define:
\includegraphics[max width=\textwidth]{2022_05_28_c7df107b7d10f7110aceg-017(1)}
[a,b)={x:a≤x<b};(a,∞)={x:a<x};(−∞,b)={x:x<b}(a,b]={x:a<x≤b};[a,∞)={x:a≤x};(−∞,b]={x:x≥b}
[ ∞ no es ningún número real, es sólo notación]
Se llama entorno de centro a y radio r>0 a B(a,r)={x:|x−a|<r}=(a−r,a+r)
[es decir, al intervalo abierto de longitud 2r centrado en a:a−a⏞−O ]
Los intervalos abiertos y cerrados son casos particulares de un tipo de conjuntos que son importantes en matemáticas más avanzadas: los conjuntos abiertos y cerrados que vamos a definir:
Def.
Sea A⊂R y a∈A.a es punto interior a A si existe r>0 tal que B(a,r)⊂A.\\
A es abierto si todos sus puntos son interiores.
Def.
Sea A⊂R.p es punto de acumulación de A si en [p no tiene que
todo entorno de p existen puntos de A distintos de p. estar en A].
Es decir, si llamamos B∗(p,r)=B(p,r)−{r}={x:0<|x−p|<r}, p es de acumulación de A si para todo r>0 es A∩B∗(p,r)≠ϕ.
\includegraphics[max width=\textwidth]{2022_05_28_c7df107b7d10f7110aceg-017(2)}
Def. A es cerrado si contiene a todos sus puntos de acumulación.
Ej. [a,b] no es abierto porque no todos sus puntos son interiores; hay dos de ellos que no lo son: a y b (los demás sí lo son); por muy pequeño que sea r, B(a, r) \not \subset[a, b] (hay puntos de B(a, r), los de la izquierda de a, que no son de [a, b]). Para ver si es cerrado, localicemos sus puntos de acumulación: cualquier p \notin[a, b] no lo es, ya que un entorno suyo suficientemente pequeño no contiene ningún punto del intervalo; todo p \in[a, b] (incluidos a \mathrm{y} b ) es de acumulación pues cualquier entorno suyo contiene infinitos puntos de [a, b]. Como [a, b] contiene a todos sus puntos de acumulación, es cerrado. 1. Naturales, enteros, racionales y reales
\begin{abstract} \(\left.C_{0}++_{\mathrm{x}}^{+}\right)_{2 \mathrm{x}}(0, \infty)\) sí es abierto, pues todos sus puntos son interiores. En efecto, sea \(x \in(0, \infty) . \exists r=x\) (o cualquier \(r<x\) ) tal que \(B(x, r)=(0,2 x) \subset(0, \infty)\). \((0, \infty)\) no es cerrado, pues \(0 \notin(0, \infty)\) y es de acumulación del conjunto. \end{abstract}
\left\{\frac{1}{n}: n \in \mathbf{N}\right\} tiene un único punto de acumulación (el 0) que no pertenece al conjunto: no es cerrado. Tampoco es abierto, pues
\includegraphics[max width=\textwidth]{2022_05_28_c7df107b7d10f7110aceg-018}\\
tiene puntos no interiores (ninguno lo es).
\{n \in \mathbf{N}: n es divisor de 12\}=\{1,2,3,4,6,12\} es claro que tampoco es abierto (puntos no interiores), pero este conjunto sí es cerrado, pues contiene a todos sus puntos de acumulación (al conjunto \phi (no hay ninguno)).
Teorema: A es cerrado si y solo si su complementario \mathbf{R}-A es abierto.
Sea A cerrado: tomemos cualquier a \in \mathbf{R}-A \Leftrightarrow a \notin A \Rightarrow a no es de acumulación de A \Rightarrow \exists r tal que B(a, r) \cap A=\phi \Rightarrow B(a, r) \subset \mathbf{R}-A \Rightarrow \mathbf{R}-A es abierto
Sea \mathbf{R}-A abierto. Probemos que A es cerrado probando: ' a \notin A \Rightarrow a no es de ac. de A ': a \notin A \Rightarrow a \in \mathbf{R}-A abierto \Rightarrow \exists r / B(a, r) \subset \mathbf{R}-A \Rightarrow B(a, r) \cap A=\phi \Rightarrow a no es de ac.

