6.3: Teorema de Burnside
- Page ID
- 117075
El Teorema de Burnside nos permitirá contar las órbitas, es decir, los diferentes colorantes, en una variedad de problemas. Primero necesitamos algunos lemmas.
Si\(c\) es una coloración,\([c]\) es la órbita de\(c\), es decir, la clase de equivalencia de\(c\). Dejar\(G(c)\) ser el conjunto de permutaciones en\(G\) ese arreglo\(c\), es decir, aquellas\(\phi\) tales que\(\phi(c)=c\); la permutación en la Figura 6.2.4 fija la coloración en la fila inferior, por ejemplo.
Lema \(\PageIndex{1}\)
\(G(c)\)es un grupo de permutaciones.
- Prueba
-
Comprobamos las propiedades de un grupo desde la Definición 6.2.1.
Supongamos\(\phi\) y\(\sigma\) ambos arreglan\(c\); entonces\(\phi(\sigma(c))=\phi(c)=c\), así\(\phi\circ\sigma\) corrige\(c\) y\(\phi\circ\sigma\in G(c)\).
La permutación de identidad fija todos los colorantes, entonces\(\id\in G(c)\).
Si\(\phi(c)=c\) entonces\(\phi^{-1}(c)=\phi^{-1}(\phi(c))=\id(c)=c\), así\(\phi^{-1}\in G(c)\).
Lema \(\PageIndex{2}\)
\(|G|=|[c]|\cdot|G(c)|\).
- Prueba
-
Para\(\phi\) y\(\sigma\) en\(G\), defina\(\phi\sim\sigma\) si\(\sigma^{-1}\circ\phi\in G(c)\). Esta es una relación de equivalencia:
- \(\sigma^{-1}\circ\sigma\) is la función de identidad, que está en\(G(c)\). Thus \(\sigma\sim\sigma\), so the relation is reflexive.
- Si\(\phi\sim\sigma\), \(\sigma^{-1}\circ\phi\in G(c)\). Entonces\((\sigma^{-1}\circ\phi)^{-1}\in G(c)\), y\((\sigma^{-1}\circ\phi)^{-1}=\phi^{-1}\circ\sigma\in G(c)\), entonces\(\sigma\sim\phi\) and \(\sim\) is symmetric.
- Si\(\phi\sim\sigma\) and \(\sigma\sim\tau\), then \(\sigma^{-1}\circ\phi\in G(c)\) y\(\tau^{-1}\circ\sigma\in G(c)\), así\((\tau^{-1}\circ\sigma)\circ(\sigma^{-1}\circ\phi)\in G(c)\). Dado que\((\tau^{-1}\circ\sigma)\circ(\sigma^{-1}\circ\phi)=\tau^{-1}\circ\phi\),\(\phi\sim\tau\), and \(\sim\) is transitive.
Ahora afirmamos que la clase de equivalencia de\(\phi\) es\(A=\{\phi\circ\sigma\mid\sigma\in G(c)\}\). Primero, supongamos que\(\sigma\in G(c)\); luego\(\phi^{-1}\circ\phi\circ\sigma=\sigma\in G(c)\), así\(\phi\circ\sigma\sim\phi\) y\(A\subseteq[\phi]\). A continuación, supongamos\(\phi\sim\tau\), así\(\tau^{-1}\circ\phi=\gamma\in G(c)\). Entonces\(\phi\circ\gamma^{-1}=\tau\), así\(\tau\in A\) y\([\phi]\subseteq A\).
Ahora mostramos que cada clase de equivalencia tiene el mismo tamaño que\(G(c)\). Definir\(f\colon G(c)\to \{\phi\circ\sigma\mid\sigma\in G(c)\}\) por\(f(\gamma)=\phi\circ\gamma\). Si\(f(\gamma_1)=f(\gamma_2)\), entonces\[\eqalign{ \phi\circ\gamma_1&=\phi\circ\gamma_2\cr \phi^{-1}\circ\phi\circ\gamma_1&=\phi^{-1}\circ\phi\circ\gamma_2\cr \gamma_1&=\gamma_2\cr }\nonumber\] así\(f\) es 1—1. Ya que cada\(\phi\circ\gamma\in\{\phi\circ\sigma\mid\sigma\in G(c)\}\) es\(f(\gamma)\),\(f\) está en.
Así es el número de clases de equivalencia\(|G|/|G(c)|\).
Por último, mostramos que el número de clases de equivalencia es\(|[c]|\). Que el conjunto de clases de equivalencia\(G\) sea\(E\), es decir,\(E=\{[\phi]\mid \phi\in G\}\). Definimos\(g\colon [c]\to E\) y mostramos que\(g\) es una bijección. Supongamos\(d\in[c]\), así que\(d=\sigma(c)\) para algunos\(\sigma\in G\). Vamos\(g(d)=[\sigma]\).
Primero, mostramos que\(g\) está bien definido. Si\(d=\sigma_1(c)=\sigma_2(c)\), entonces\(\sigma_2^{-1}\circ\sigma_1(c)=c\), así\(\sigma_1\sim\sigma_2\) y\([\sigma_1]=[\sigma_1]\), es decir,\(g(\sigma_1)=g(\sigma_2)\).
Siguiente, supongamos\(g(d_1)=g(d_2)\). Esto significa que\(d_1=\sigma_1(c)\),\(d_2=\sigma_2(c)\), y\([\sigma_1]=[\sigma_2]\). De ahí\(\sigma_2^{-1}\circ\sigma_1(c)=c\), así\(\sigma_1(c)=\sigma_2(c)\) y así\(d_1=d_2\), así\(g\) es 1—1.
Supongamos que\([\sigma]\in E\). Entonces\(g(\sigma(c))=[\sigma]\), así\(g\) es sobre.
Así tenemos\[|[c]|=|E|={|G|\over|G(c)|}\nonumber\] y\[|G(c)|\cdot|[c]|=|G|\nonumber\] como se desee.
Corolario \(\PageIndex{1}\)
Si\(c\sim d\) entonces\(|G(c)|=|G(d)|\).
- Prueba
-
Desde\(c\sim d\),\([c]=[d]\), y\[\eqalign{ {|G|\over|G(c)|} = |[c]|&=|[d]|= {|G|\over|G(c)|}\cr |G(c)|&=|G(d)|\cr }\nonumber \]
Definición\(\PageIndex{1}\)
Si el grupo\(G\) actúa sobre los colorantes de un objeto y\(\sigma\in G\),\(\text{fix}(\sigma)\) es el conjunto de colorantes que se fijan por\(\sigma\).
Teorema \(\PageIndex{1}\): Burnside's Theorem
Si el grupo\(G\) actúa sobre los colorantes de un objeto, el número de colores distintos módulo\(G\) es\[{1\over|G|}\sum_{\sigma\in G} |\text{fix}(\sigma)|.\nonumber \]
- Prueba
-
Deja\(C\) ser el conjunto de todos los colorantes, y deja\(\cal O\) ser el conjunto de órbitas. Dejar\(c_1,c_2,\ldots,c_k\) ser una lista de colorantes, uno en cada órbita, para que las órbitas sean\([c_1],[c_2],\ldots,[c_k]\). Considera la suma\(\sum_{c\in C}|G(c)|\):
\[\eqalign{ \sum_{c\in C}|G(c)|&=\sum_{i=1}^k\sum_{c\in[c_i]}|G(c)|\cr &=\sum_{i=1}^k\sum_{c\in[c_i]}|G(c_i)|\cr &=\sum_{i=1}^k\sum_{c\in[c_i]}{|G|\over|[c_i]|}\cr &=\sum_{i=1}^k |[c_i]|{|G|\over|[c_i]|}\cr &=\sum_{i=1}^k |G|=|G|\sum_{i=1}^k 1 = |G||{\cal O}|.\cr }\nonumber\]Entonces\[|{\cal O}| = {1\over|G|}\sum_{c\in C}|G(c)|.\nonumber \]
Esto ya da una fórmula interesante para\(|{\cal O}|\), pero es difícil de manejar, ya que el número de colorantes suele ser bastante grande; efectivamente, dado que normalmente queremos calcular el número de órbitas para\(k\) los colores, el número de colorantes no es un número fijo.
Con solo un poco más de trabajo podemos solucionar este problema:\[\eqalign{ \sum_{c\in C}|G(c)|&=\sum_{c\in C}\sum_{\sigma\in G(c)} 1\cr &=\sum_{\sigma\in G}\sum_{c\in \text{fix}(\sigma)} 1\cr &=\sum_{\sigma\in G}|\text{fix}(\sigma)|.\cr }\nonumber\] Ahora\[|{\cal O}| = {1\over|G|}\sum_{\sigma\in G}|\text{fix}(\sigma)|\nonumber\] como se desee.
Dado que el grupo de permutaciones en un problema típico es bastante pequeño, la suma en el Teorema de Burnside suele ser manejable. Además, podemos hacer que la tarea de la computación sea\(|\text{fix}(\sigma)|\) bastante sencilla. Consideremos un ejemplo particular, la permutación de la Figura 6.2.4, mostrada nuevamente en la Figura\(\PageIndex{1}\). Si estamos usando\(k\) colores, ¿cuántos colorantes del pentágono están fijados por esta permutación? Dado que la permutación intercambia los vértices 2 y 5, deben ser del mismo color si\(\phi\) es para fijar la coloración. De igual manera los vértices 3 y 4 deben ser del mismo color; el vértice 1 puede ser de cualquier color. Así, el número de colorantes fijados por\(\phi\) es\(k^3\). Es fácil ver que cada permutación “flip” del pentágono es esencialmente la misma, así que para cada una de las cinco permutaciones flip, el tamaño de\(\text{fix}(\sigma)\) is\(k^3\).
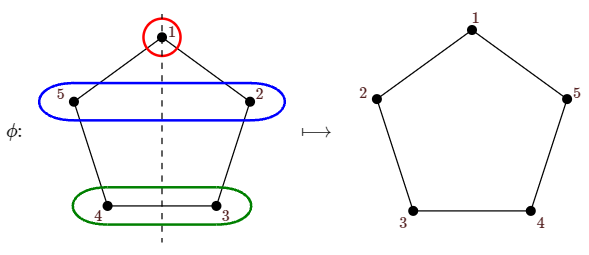
Toda permutación puede escribirse en forma de ciclo: La permutación en Figura\(\PageIndex{1}\), por ejemplo, es\((1)(2,5)(3,4)\). Un ciclo en este contexto es una secuencia\((x_1,x_2,\ldots,x_k)\), es decir\(\phi(x_1)=x_2\), eso\(\phi(x_2)=x_3)\),, y así sucesivamente hasta\(\phi(x_k)=x_1\). Siguiendo nuestro razonamiento anterior, los vértices en cada ciclo deben ser coloreados del mismo color, y el número total de colores fijados por\(\phi\) es\(k^m\), donde\(m\) está el número de ciclos.
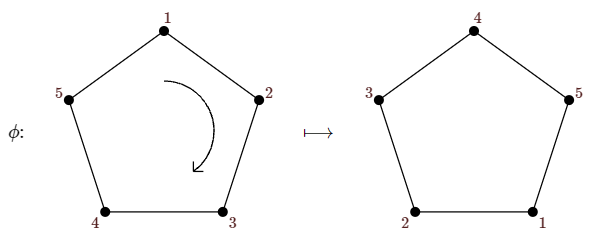
Let's apply this to another permutation, shown in Figure \(\PageIndex{2}\). This permutation consists of a single cycle, so every vertex must have the same color, and the number of colorings fixed by \(\phi\) is \(k^1\). All rotations of the pentagon consist of a single cycle except the trivial rotation, that is, the identity permutation. In cycle form, the identity permutation is \((1)(2)(3)(4)(5)\), so the number of colorings fixed by the identity is \(k^5\). Putting everything together, we thus have \[|{\cal O}|={1\over 10}(k^5+k+k+k+k+k^3+k^3+k^3+k^3+k^3)= {1\over 10}(k^5+5k^3+4k).\nonumber\] For example, the number of different 3-colorings is \((3^5+5\cdot3^3+4\cdot 3)/10=39\).
We find the number of distinct colorings of the vertices of a square with \(k\) colors, modulo \(D_4\), the dihedral group of size 8. The elements of \(D_4\) are the four rotations \(r_0\), \(r_{90}\), \(r_{180}\), \(r_{270}\), where \(r_i\) is the counterclockwise rotation by \(i\) degrees, and the four reflections \(f_H\), \(f_V\), \(f_D\), \(f_A\), as indicated in Figure \(\PageIndex{3}\).
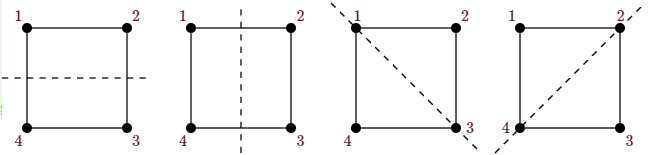
In cycle notation these permutations are: \[\eqalign{ r_0&=(1)(2)(3)(4)\cr r_{90}&=(1,4,3,2)\cr r_{180}&=(1,3)(2,4)\cr r_{270}&=(1,2,3,4)\cr f_H&=(1,4)(2,3)\cr f_V&=(1,2)(3,4)\cr f_D&=(1)(2,4)(3)\cr f_A&=(1,3)(2)(4).\cr }\nonumber\] so the number of colorings is \[f(k)={1\over 8}(k^4+k+k^2+k+k^2+k^2+k^3+k^3)={1\over8}(k^4+2k^3+3k^2+2k).\nonumber\] For example, \(f(2)=6\); the six colorings are shown in Figure \(\PageIndex{4}\).

Here is a more complicated example: how many different graphs are there on four vertices? In this case, of course, "different'' means "non-isomorphic''. We can interpret this as a coloring problem: Color the edges of the complete graph \(K_4\) with two colors, say black and white. The black edges form a graph; the white edges are the ones left out of the graph. The group \(G\) we need to consider is all permutations of the six edges of \(K_4\) induced by a permutation of the vertices, so \(|G|=4!=24\). All we need to know is the number of cycles in each permutation; we consider a number of cases.
Case 1. The identity permutation on the vertices induces the identity permutation on the edges, with 6 cycles, so the contribution to the sum is \(2^6\).
Case 2. A 4-cycle on the vertices induces a permutation of the edges consisting of one 4-cycle and one 2-cycle, that is, two cycles. There are \(3!=6\) 4-cycles on the vertices, so the contribution of all of these is \(6\cdot2^2\).
Case 3. A permutation of the vertices consisting of a 3-cycle and a 1-cycle induces a permutation of the edges consisting of two 3-cycles. There are \(4\cdot2=8\) such permutations of the vertices, so the contribution of all is \(8\cdot2^2\).
Case 4. A permutation of the vertices consisting of two 2-cycles induces a permutation of the edges consisting of two 1-cycles and two 2-cycles. There are \({1\over2}{4\choose2}=3\) such permutations, so the contribution is \(3\cdot 2^4\).
Case 5. A permutation of the vertices consisting of a 2-cycle and two 1-cycles induces a permutation of the edges consisting of two 1-cycles and two 2-cycles. There are \({4\choose2}=6\) such permutations, so the contribution is \(6\cdot 2^4\).
The number of distinct colorings, that is, the number of distinct graphs on four vertices, is
\[{1\over24}(2^6+6\cdot2^2+8\cdot2^2+3\cdot 2^4+6\cdot2^4)= {1\over24}(264)=11.\nonumber\]
It is possible, though a bit difficult, to see that for \(n\) vertices the result is
\[\label{eq:1}\eqalignno{ f(n)&=\sum_{\bf j}\prod_{k=1}^n{1\over k^{j_k} j_k!} \prod_{k=1}^{\lfloor n/2\rfloor}2^{k j_{2k}} \!\!\prod_{k=1}^{\lfloor (n-1)/2\rfloor}\!\!2^{kj_{2k+1}} \prod_{k=1}^{\lfloor n/2\rfloor} 2^{kC(j_k,2)} \!\!\!\!\prod_{1\le r< s\le n-1}\!\!\!\!\!\!\!\! 2^{\gcd(r,s)j_rj_s}\cr} \]
where the sum is over all partitions \({\bf j}=(j_1,j_2,\ldots,j_n)\) of \(n\), that is, over all \(\bf j\) such that \(j_1+2j_2+3j_3+\cdots+nj_n=n\), and \(C(m,2)={m\choose2}\). With this formula and a computer it is easy to compute the number of graphs when \(n\) is not too large; for example, \(f(5)=34\), so there are 34 different five-vertex graphs.
In light of the forgoing discussion, we can restate Theorem \(\PageIndex{1}\). If \(\sigma\) is a permutation, let \(\#\sigma\) denote the number of cycles when \(\sigma\) is written in cycle form.
If group \(G\) acts on the colorings of an object, the number of distinct colorings modulo \(G\) with \(k\) colors is \[{1\over|G|}\sum_{\sigma\in G} k^{\#\sigma}.\nonumber\]


