A.1: Vectores, asignaciones y matrices

En la vida real, la mayoría de las veces hay más de una variable. Deseamos organizar el tratamiento de múltiples variables de manera consistente, y en particular organizar el tratamiento de ecuaciones lineales y mapeos lineales, ya que son bastante útiles y bastante fáciles de manejar. Los matemáticos bromean eso Y bueno, ellos (los ingenieros) no se equivocan. Muy a menudo, resolver un problema de ingeniería es averiguar el problema lineal finito-dimensional correcto a resolver, que luego se resuelve con alguna manipulación matricial. Lo más importante es que los problemas lineales son los que sabemos resolver, y tenemos muchas herramientas para resolverlos. Para ingenieros, matemáticos, físicos y cualquier otra persona en un campo técnico, es absolutamente vital aprender álgebra lineal.

Como motivación, supongamos que deseamos resolver\[\begin{align}\begin{aligned} & x-y = 2 , \\ & 2x+y = 4 , \end{aligned}\end{align} \nonumber \] por\(x\) y\(y\). Es decir, deseamos números\(x\) y\(y\) tal que se satisfagan las dos ecuaciones. Empecemos quizás sumando las ecuaciones para encontrar\[x+2x-y+y = 2+4, \qquad \text{or} \qquad 3x = 6 . \nonumber \]

En otras palabras,\(x=2\). Una vez que tenemos eso, nos conectamos\(x=2\) a la primera ecuación para encontrar\(2-y=2\), entonces\(y=0\). Bien, eso fue fácil. Qué es todo este alboroto sobre las ecuaciones lineales. Bueno, intenta hacer esto si tienes\(5000\) incógnitas \(^{1}\). También, podemos tener tales ecuaciones no sólo de números, sino de funciones y derivadas de funciones en ecuaciones diferenciales. Claramente necesitamos una forma sistemática de hacer las cosas. Una buena consecuencia de hacer las cosas sistemáticas y más sencillas de escribir es que se vuelve más fácil que las computadoras hagan el trabajo por nosotros. Las computadoras son bastante estúpidas, no piensan, pero son muy buenas para hacer muchas tareas repetitivas precisamente, siempre y cuando descubramos una manera sistemática para que realicen las tareas.

Vectores y operaciones sobre vectores

Considerar los números\(n\) reales como una\(n\) -tupla:\[(x_1,x_2,\ldots,x_n). \nonumber \] El conjunto de tales\(n\) -tuplas es el llamado espacio\(n\) -dimensional, a menudo denotado por\({\mathbb R}^n\). A veces llamamos a esto el espacio euclidiano\(n\) -dimensional \(^{2}\). En dos dimensiones,\({\mathbb R}^2\) se llama el plano cartesiano \(^{3}\). Cada una\(n\) de esas tuplas representa un punto en el espacio\(n\) -dimensional. Por ejemplo, el punto\((1,2)\) en el plano\({\mathbb R}^2\) es una unidad a la derecha y dos unidades hacia arriba desde el origen.

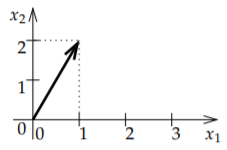
Cuando hacemos álgebra con estas\(n\) -tuplas de números las llamamos vectores \(^{4}\). Los matemáticos están interesados en separar lo que es un vector y lo que es un punto del espacio o en el plano, y resulta ser una distinción importante, sin embargo, a los efectos del álgebra lineal podemos pensar en que todo esté representado por un vector. Una manera de pensar en un vector, que es especialmente útil en cálculo y ecuaciones diferenciales, es una flecha. Es un objeto que tiene una dirección y una magnitud. Por ejemplo, el vector\((1,2)\) es la flecha desde el origen hasta el punto\((1,2)\) en el plano. La magnitud es la longitud de la flecha. Ver Figura\(\PageIndex{1}\). Si pensamos en los vectores como flechas, la flecha no siempre tiene que comenzar por el origen. Si lo hacemos moverse, sin embargo, siempre debe mantener la misma dirección y la misma magnitud.

Figura\(\PageIndex{1}\): El vector\((1,2)\) dibujado como una flecha desde el origen hasta el punto\((1,2)\).

Como vectores son flechas, cuando queremos darle un nombre a un vector, dibujamos una pequeña flecha encima de él:\[\vec{x} \nonumber \]

Otra notación popular es\(\mathbf{x}\), aunque usaremos las pequeñas flechas. Puede ser fácil escribir una letra en negrita en un libro, pero no es tan fácil escribirla a mano en papel o en la pizarra. Los matemáticos a menudo ni siquiera escriben las flechas. Un matemático escribiría\(x\) y solo recordaría que\(x\) es un vector y no un número. Así como recuerdas que Bob es tu tío, y no tienes que seguir repitiendo y solo puedes decir En este libro, sin embargo, llamaremos a Bob y escribiremos vectores con las pequeñas flechas.

La magnitud se puede calcular utilizando el teorema de Pitágoras. El vector\((1,2)\) dibujado en la figura tiene magnitud\(\sqrt{1^2+2^2} = \sqrt{5}\). La magnitud se denota por\(\lVert \vec{x} \rVert\), y, en cualquier número de dimensiones, se puede calcular de la misma manera:\[\lVert \vec{x} \rVert = \lVert (x_1,x_2,\ldots,x_n) \rVert = \sqrt{x_1^2+x_2^2+\cdots+x_n^2} . \nonumber \]

Por razones que quedarán claras en la siguiente sección, a menudo escribimos vectores como los llamados vectores de columna:\[\vec{x} = \begin{bmatrix} x_{1} \\ x_2 \\ \vdots \\ x_n \end{bmatrix} . \nonumber \]

No te preocupes. Es solo una forma diferente de escribir lo mismo, y será útil más adelante. Por ejemplo, el vector se\((1,2)\) puede escribir como\[\begin{bmatrix} 1 \\ 2 \end{bmatrix} . \nonumber \]

El hecho de que escribamos flechas por encima de los vectores nos permite escribir varios vectores\(\vec{x}_1\)\(\vec{x}_2\),, etc., sin confundirlos con los componentes de algún otro vector\(\vec{x}\).

Entonces, ¿dónde está el álgebra del álgebra lineal? Bueno, las flechas se pueden sumar, restar y multiplicar por números. Primero consideramos la adición. Si tenemos dos flechas, simplemente nos movemos a lo largo de una, y luego a lo largo de la otra. Ver Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Sumando los vectores\((1,2)\), dibujados punteados y\((2,-3)\), dibujados discontinuados. El resultado,\((3,-1)\), se dibuja como una flecha sólida.

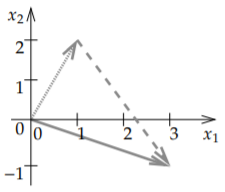
Es bastante fácil ver qué le hace a los números que representan a los vectores. Supongamos que queremos agregar\((1,2)\) a\((2,-3)\) como en la figura. Viajamos\((1,2)\) y luego viajamos a lo largo\((2,-3)\). Lo que hicimos fue viajar una unidad a la derecha, dos unidades arriba, y luego viajamos dos unidades a la derecha, y tres unidades abajo (las tres negativas). Eso significa que terminamos en\(\bigl(1+2,2+(-3)\bigr) = (3,-1)\). Y así es como siempre funciona la adición:\[\begin{bmatrix} x_{1} \\ x_2 \\ \vdots \\ x_n \end{bmatrix} + \begin{bmatrix} y_{1} \\ y_2 \\ \vdots \\ y_n \end{bmatrix} = \begin{bmatrix} x_1 + y_{1} \\ x_2+ y_2 \\ \vdots \\ x_n + y_n \end{bmatrix} . \nonumber \]

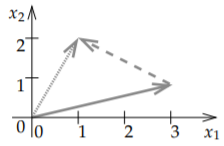
Restar es similar. Lo que\(\vec{x}- \vec{y}\) significa visualmente es que primero viajamos a lo largo\(\vec{x}\), y luego viajamos hacia atrás\(\vec{y}\). Ver Figura\(\PageIndex{3}\). Es como agregar\(\vec{x}+ (- \vec{y})\) dónde\(-\vec{y}\) está la flecha que obtenemos borrando la cabeza de flecha de un lado y dibujándola por el otro lado, es decir, invertimos la dirección. En cuanto a los números, simplemente vamos hacia atrás tanto horizontal como verticalmente, por lo que negamos ambos números. Por ejemplo, si\(\vec{y}\) es\((-2,1)\), entonces\(-\vec{y}\) es\((2,-1)\).

Figura\(\PageIndex{3}\): Resta, el vector\((1,2)\), dibujado punteado, menos\((-2,1)\), dibujado discontinuo. El resultado,\((3,1)\), se dibuja como una flecha sólida.

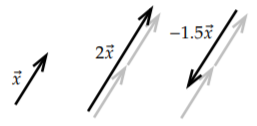
Otra cosa intuitiva que hacer a un vector es escalarlo. Esto lo representamos multiplicando un número con un vector. Debido a esto, cuando deseamos distinguir entre vectores y números, llamamos a los números escalares. Por ejemplo, supongamos que queremos viajar tres veces más allá. Si el vector es\((1,2)\), viajar 3 veces más significa ir 3 unidades a la derecha y 6 unidades hacia arriba, así obtenemos el vector\((3,6)\). Simplemente multiplicamos cada número en el vector por 3. Si\(\alpha\) es un número, entonces\[\alpha \begin{bmatrix} x_{1} \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} \alpha x_{1} \\ \alpha x_2 \\ \vdots \\ \alpha x_n \end{bmatrix} . \nonumber \] Escalar (por un número positivo) multiplica la magnitud y deja la dirección intacta. La magnitud de\((1,2)\) es\(\sqrt{5}\). La magnitud de 3 veces\((1,2)\), es decir,\((3,6)\), es\(3\sqrt{5}\).

Cuando el escalar es negativo, entonces cuando multiplicamos un vector por él, el vector no solo se escala, sino que también cambia de dirección. Multiplicando\((1,2)\) por\(-3\) medios debemos ir 3 veces más allá pero en sentido contrario, así 3 unidades a la izquierda y 6 unidades hacia abajo, o en otras palabras,\((-3,-6)\). Como mencionamos anteriormente,\(-\vec{y}\) es un revés de\(\vec{y}\), y esto es lo mismo que\((-1)\vec{y}\).

En Figura\(\PageIndex{4}\), puedes ver un par de ejemplos de lo que significa visualmente escalar un vector.

Figura\(\PageIndex{4}\): Un vector\(\vec{x}\), el vector\(2\vec{x}\) (misma dirección, doble de magnitud) y el vector\(-1.5\vec{x}\) (dirección opuesta,\(1.5\) multiplicada por la magnitud).

Juntamos todas estas operaciones para elaborar expresiones más complicadas. Vamos a calcular un pequeño ejemplo:\[3 \begin{bmatrix} 1 \\ 2 \end{bmatrix} + 2 \begin{bmatrix} -4 \\ -1 \end{bmatrix} - 3 \begin{bmatrix} -2 \\ 2 \end{bmatrix} = \begin{bmatrix} 3(1)+2(-4)-3(-2) \\ 3(2)+2(-1)-3(2) \end{bmatrix} = \begin{bmatrix} 1 \\ -2 \end{bmatrix} . \nonumber \]

Como dijimos un vector es una dirección y una magnitud. La magnitud es fácil de representar, es solo un número. La dirección suele estar dada por un vector con magnitud uno. Llamamos a tal vector un vector unitario. Es decir,\(\vec{u}\) es un vector unitario cuando\(\lVert \vec{u} \rVert = 1\). Por ejemplo, los vectores\((1,0)\),\((\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\), y\((0,-1)\) son todos vectores unitarios.

Para representar la dirección de un vector\(\vec{x}\), necesitamos encontrar el vector unitario en la misma dirección. Para ello, simplemente reescalamos\(\vec{x}\) por el recíproco de la magnitud, es decir\(\frac{1}{\lVert \vec{x} \rVert} \vec{x}\), o de manera más concisa\(\frac{\vec{x}}{\lVert \vec{x} \rVert}\).

Como ejemplo, el vector unitario en la dirección de\((1,2)\) es el vector\[\frac{1}{\sqrt{1^2+2^2}} (1,2) = \left( \frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}} \right) . \nonumber \]

Mapeos Lineales y Matrices

Una función con valor vectorial\(F\) es una regla que toma un vector\(\vec{x}\) y devuelve otro vector\(\vec{y}\). Por ejemplo,\(F\) podría ser un escalado que duplique el tamaño de los vectores:\[F(\vec{x}) = 2 \vec{x} . \nonumber \] Aplicado a decir que\((1,3)\) obtenemos\[F \left( \begin{bmatrix} 1 \\ 3 \end{bmatrix} \right) = 2 \begin{bmatrix} 1 \\ 3 \end{bmatrix} = \begin{bmatrix} 2 \\ 6 \end{bmatrix} . \nonumber \] Si\(F\) es un mapeo que toma vectores en\({\mathbb R}^2\)\({\mathbb R}^2\) (como el anterior), escribimos\[F \colon {\mathbb R}^2 \to {\mathbb R}^2 . \nonumber \]

Las palabras función y mapeo se usan de manera bastante intercambiable, aunque la mayoría de las veces, el mapeo se usa cuando se habla de una función de valor vectorial, y la función de palabra se usa a menudo cuando la función es de valor escalar.

Un estudiante principiante de matemáticas (y muchos un matemático experimentado), que ve una expresión como\[f(3x+8y) \nonumber \] anhelos escribir\[3f(x)+8f(y) . \nonumber \]

Después de todo, que no ha querido escribir\(\sqrt{x+y} = \sqrt{x} + \sqrt{y}\) o algo así en algún momento de su vida matemática. ¿La vida no sería sencilla si pudiéramos hacer eso? Por supuesto que no siempre podemos hacer eso (¡por ejemplo, no con las raíces cuadradas!) Pero hay muchas otras funciones donde podemos hacer exactamente lo anterior. Tales funciones se llaman lineales.

Un mapeo\(F \colon {\mathbb R}^n \to {\mathbb R}^m\) se llama lineal si\[F(\vec{x}+\vec{y}) = F(\vec{x})+F(\vec{y}), \nonumber \] para cualquier vector\(\vec{x}\) y\(\vec{y}\), y también\[F(\alpha \vec{x}) = \alpha F(\vec{x}) , \nonumber \] para cualquier escalar\(\alpha\). El que\(F\) definimos anteriormente que duplica el tamaño de todos los vectores es lineal. Verifiquemos:\[F(\vec{x}+\vec{y}) = 2(\vec{x}+\vec{y}) = 2\vec{x}+2\vec{y} = F(\vec{x})+F(\vec{y}) , \nonumber \] y también\[F(\alpha \vec{x}) = 2 \alpha \vec{x} = \alpha 2 \vec{x} = \alpha F(\vec{x}) . \nonumber \]

También llamamos a una función lineal una transformación lineal. Si quieres ser realmente elegante e impresionar a tus amigos, puedes llamarlo operador lineal. Cuando un mapeo es lineal, a menudo no escribimos los paréntesis. Escribimos simplemente\[F \vec{x} \nonumber \] en lugar de\(F(\vec{x})\). Esto lo hacemos porque linealidad significa que el mapeo\(F\) se comporta como multiplicar\(\vec{x}\) por Eso algo es una matriz.

Una matriz es una\(m \times n\) matriz de números (\(m\)filas y\(n\) columnas). Una\(3 \times 5\) matriz es\[A = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} & a_{15} \\ a_{21} & a_{22} & a_{23} & a_{24} & a_{25} \\ a_{31} & a_{32} & a_{33} & a_{34} & a_{35} \end{bmatrix} . \nonumber \] Los números\(a_{ij}\) se llaman elementos o entradas.

Un vector de columna es simplemente una\(m \times 1\) matriz. De manera similar a un vector de columna también hay un vector de fila, que es una\(1 \times n\) matriz. Si tenemos una\(n \times n\) matriz, entonces decimos que es una matriz cuadrada.

Ahora, ¿cómo\(A\) se relaciona una matriz con un mapeo lineal? Bueno una matriz te dice a dónde van ciertos vectores especiales. Vamos a darle un nombre a esos ciertos vectores. La base estándar de vectores de\({\mathbb R}^n\) son\[\vec{e}_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} , \qquad \vec{e}_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} , \qquad \vec{e}_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix} , \qquad \cdots , \qquad \vec{e}_n = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix} . \nonumber \] En\({\mathbb R}^3\) estos vectores son\[\vec{e}_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} , \qquad \vec{e}_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} , \qquad \vec{e}_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} . \nonumber \] Puede recordar del cálculo de varias variables que a estas a veces se les llama\(\vec{\imath}\),\(\vec{\jmath}\),\(\vec{k}\).

La razón por la que estos se llaman base es que todos los demás vectores pueden escribirse como una combinación lineal de ellos. Por ejemplo, en\({\mathbb R}^3\) el vector se\((4,5,6)\) puede escribir como\[4 \vec{e}_1 + 5 \vec{e}_2 + 6 \vec{e}_3 = 4 \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + 5 \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} + 6 \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 4 \\ 5 \\ 6 \end{bmatrix} . \nonumber \]

Entonces, ¿cómo representa una matriz un mapeo lineal? Bueno, las columnas de la matriz son los vectores donde\(A\) como toma un mapeo lineal\(\vec{e}_1\)\(\vec{e}_2\),, etc. por ejemplo, considere\[M = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} . \nonumber \]

Como un mapeo lineal\(M \colon {\mathbb R}^2 \to {\mathbb R}^2\) toma\(\vec{e}_1 = \left[ \begin{smallmatrix} 1 \\ 0 \end{smallmatrix} \right]\) hacia\(\left[ \begin{smallmatrix} 1 \\ 3 \end{smallmatrix} \right]\) y\(\vec{e}_2 = \left[ \begin{smallmatrix} 0 \\ 1 \end{smallmatrix} \right]\) hacia\(\left[ \begin{smallmatrix} 2 \\ 4 \end{smallmatrix} \right]\). En otras palabras,\[M \vec{e}_1 = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ 3 \end{bmatrix}, \qquad \text{and} \qquad M \vec{e}_2 = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 4 \end{bmatrix}. \nonumber \]

De manera más general, si tenemos una\(n \times m\) matriz\(A\), es decir, tenemos\(n\) filas y\(m\) columnas, entonces el mapeo\(A \colon {\mathbb R}^m \to {\mathbb R}^n\) lleva\(\vec{e}_j\) a la\(j^{\text{th}}\) columna de\(A\). Por ejemplo,\[A = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} & a_{15} \\ a_{21} & a_{22} & a_{23} & a_{24} & a_{25} \\ a_{31} & a_{32} & a_{33} & a_{34} & a_{35} \end{bmatrix} \nonumber \] representa una asignación de\({\mathbb R}^5\) a\({\mathbb R}^3\) que hace\[A \vec{e}_1 = \begin{bmatrix} a_{11} \\ a_{21} \\ a_{31} \end{bmatrix} , \qquad A \vec{e}_2 = \begin{bmatrix} a_{12} \\ a_{22} \\ a_{32} \end{bmatrix} , \qquad A \vec{e}_3 = \begin{bmatrix} a_{13} \\ a_{23} \\ a_{33} \end{bmatrix} , \qquad A \vec{e}_4 = \begin{bmatrix} a_{14} \\ a_{24} \\ a_{34} \end{bmatrix} , \qquad A \vec{e}_5 = \begin{bmatrix} a_{15} \\ a_{25} \\ a_{35} \end{bmatrix} . \nonumber \]

¿Qué pasa con otro vector\(\vec{x}\), que no está en la base estándar? ¿A dónde va? Utilizamos linealidad. Primero, escribimos el vector como una combinación lineal de los vectores base estándar:\[\vec{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix} = x_1 \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} + x_2 \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} + x_3 \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} + x_4 \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} + x_5 \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} = x_1 \vec{e}_1 + x_2 \vec{e}_2 + x_3 \vec{e}_3 + x_4 \vec{e}_4 + x_5 \vec{e}_5 . \nonumber \]

Entonces\[A \vec{x} = A ( x_1 \vec{e}_1 + x_2 \vec{e}_2 + x_3 \vec{e}_3 + x_4 \vec{e}_4 + x_5 \vec{e}_5 ) = x_1 A\vec{e}_1 + x_2 A\vec{e}_2 + x_3 A\vec{e}_3 + x_4 A\vec{e}_4 + x_5 A\vec{e}_5 . \nonumber \] si sabemos dónde\(A\) lleva todos los vectores base, sabemos a dónde lleva todos los vectores.

Supongamos que\(M\) es la\(2 \times 2\) matriz de arriba, entonces\[M \begin{bmatrix} -2 \\ 0.1 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} -2 \\ 0.1 \end{bmatrix} = -2 \begin{bmatrix} 1 \\ 3 \end{bmatrix} + 0.1 \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} -1.8 \\ -5.6 \end{bmatrix} . \nonumber \]

Cada mapeo lineal de\({\mathbb R}^m\) a\({\mathbb R}^n\) puede ser representado por una\(n \times m\) matriz. Solo averiguas a dónde lleva los vectores de base estándar. Por el contrario, cada\(n \times m\) matriz representa un mapeo lineal. Por lo tanto, podemos pensar que las matrices son mapeos lineales, y los mapeos lineales son matrices.

¿O podemos? En este libro estudiamos principalmente operadores diferenciales lineales, y los operadores diferenciales lineales son mapeos lineales, aunque no están actuando sobre\({\mathbb R}^n\), sino sobre un espacio infinito-dimensional de funciones:\[L f = g . \nonumber \] Para una función\(f\) obtenemos una función\(g\), y\(L\) es lineal en el sentido que\[L ( f + h) = Lf + Lh, \qquad \text{and} \qquad L (\alpha f) = \alpha Lf . \nonumber \] para cualquier número (escalar)\(\alpha\) y todas las funciones\(f\) y\(h\).

Entonces la respuesta no es realmente. Pero si consideramos vectores en espacios finito-dimensionales\({\mathbb R}^n\) entonces sí, cada mapeo lineal es una matriz. Hemos mencionado al inicio de esta sección, que podemos Eso no es estrictamente cierto, pero es cierto aproximadamente. Esos espacios de funciones pueden ser aproximados por un espacio finito-dimensional, y luego los operadores lineales son solo matrices. Entonces aproximadamente, esto es cierto. Y en cuanto a los cálculos reales que podemos hacer en una computadora, podemos trabajar sólo con finitamente muchas dimensiones de todos modos. Si le pides a una computadora o a tu calculadora que grafique una función, toma muestras de la función en muchos puntos finitamente y luego conecta los puntos \(^{5}\). En realidad no te da infinitamente muchos valores. La forma en que has estado usando la computadora o tu calculadora hasta ahora ya ha sido una cierta aproximación del espacio de funciones por un espacio finito-dimensional.

Para terminar la sección, notamos cómo se\(A \vec{x}\) puede escribir de manera más sucintamente. Supongamos\[A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix} \qquad \text{and} \qquad \vec{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} . \nonumber \]

Entonces\[A \vec{x} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} a_{11} x_1 + a_{12} x_2 + a_{13} x_3 \\ a_{21} x_1 + a_{22} x_2 + a_{23} x_3 \end{bmatrix} . \nonumber \]

Por ejemplo, es\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 2 \\ -1 \end{bmatrix} = \begin{bmatrix} 1 \cdot 2 + 2 \cdot (-1) \\ 3 \cdot 2 + 4 \cdot (-1) \end{bmatrix} = \begin{bmatrix} 0 \\ 2 \end{bmatrix} . \nonumber \] decir, tomas las entradas en una fila de la matriz, las multiplicas por las entradas en tu vector, sumas cosas, y esa es la entrada correspondiente en el vector resultante.

Notas al pie

[1] Una de las desventajas de hacer que todo parezca un problema lineal es que el número de variables tiende a volverse enorme.

[2] El nombre del antiguo matemático griego Euclides de Alejandría (alrededor del 300 a.C.), posiblemente el más famoso de los matemáticos; incluso los pueblos pequeños suelen tener Euclid Street o Euclid Avenue.

[3] Nombrado así por el matemático francés René Descartes (1596—1650). Es como su nombre en latín es Renatus Cartesius.

[4] Una notación común para distinguir vectores de puntos es escribir\((1,2)\) para el punto y\(\langle 1,2 \rangle\) para el vector. Escribimos ambos como\((1,2)\).

[5] Si alguna vez has usado Matlab, es posible que hayas notado que para trazar una función, tomamos un vector de entradas, le pedimos a Matlab que calme el vector correspondiente de valores de la función, y luego le pedimos que grafique el resultado.