Inicio
Matemáticas
Libro: Cálculo (Apex)
1: Límites
1.E: Aplicaciones de Límites (Ejercicios)

1.E: Aplicaciones de Límites (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 111852

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

1.1: Una introducción a los límites

Términos y Conceptos

En sus propias palabras, ¿qué significa “encontrar el límite de$f(x)$ como se$x$ acerca a 3"?
Una expresión de la forma$\frac00$ se llama _____.
T/F: El límite de$f(x)$ como se$x$ acerca a 5 es$f(5)$.
Describir tres situaciones donde$\lim\limits_{x\to c}f(x)$ no existe.
En sus propias palabras, lo que es un cociente de diferencia.

Problemas

En los Ejercicios 6-16, aproximar los límites dados tanto numérica como gráficamente.

6. $\lim\limits_{x\to 1}x^2+3x-5$

7. $\lim\limits_{x\to 0}x^3-3x^2+x-5$

8. $\lim\limits_{x\to 0}\frac{x+1}{x^2+3x}$

9. $\lim\limits_{x\to 3}\frac{x^2-2x-3}{x^2-4x+3}$

10. $\lim\limits_{x\to-1}\frac{x^2+8x+7}{x^2+6x+5}$

11. $\lim\limits_{x\to 2}\frac{x^2+7x+10}{x^2-4x+4}$

12. $\lim\limits_{x\to 2}$, donde$ f(x) = \begin{cases}x+2 \quad x\le 2\\ 3x-5 \quad x>2 \end{cases}.$

13. $\lim\limits_{x\to 3}$, donde$ f(x) = \begin{cases}x^2-x+1 \quad & x\le 3\\ 2x+1 &x>3 \end{cases}.$

14. $\lim\limits_{x\to 0}$, donde$ f(x) = \begin{cases}\cos x \quad & x\le 0\\ x^2+3x+1 &x>0 \end{cases}.$

15. $\lim\limits_{x\to \pi/2}$, donde$ f(x) = \begin{cases}\sin x \quad & x\le \pi/2\\ \cos x &x>\pi/2 \end{cases}.$

En los Ejercicios 16-24,$a$ se dan una función$f$ y un valor. Aproximar el límite del cociente de diferencia,$\lim\limits_{h\to 0}\frac{f(a+h)-f(a)}{h}$, usando$h=\pm 0.1,\, \pm 0.01.$

16. $f(x)=-7x+2,\quad a=3$

17. $f(x)=9x+0.06,\quad a=-1$

18. $f(x)=x^2+3x-7,\quad a=1$

19. $f(x)=\frac{1}{x+1},\quad a=2$

20. $f(x)=-4x^2+5x-1,\quad a=-3$

21. $f(x)=\ln x,\quad a=5$

22. $f(x)=\sin x,\quad a=\pi$

23. $f(x)=\cos x,\quad a=\pi$

1.2: Definición Épsilon-Delta de un límite

Términos y Conceptos

1. ¿Qué tiene de malo la siguiente “definición” de un límite?

“El límite de$f(x)$, a medida que x se acerca$a$, es$K''$ medios que dado alguno$\delta >0$ existe$\epsilon >0$ tal que siempre que$|f(x)-K|<\epsilon$, tenemos$|x-a|<\delta$.

2. ¿Cuál se da primero en establecer un límite, la tolerancia x o la tolerancia y?

3. T/F: siempre$\epsilon$ debe ser positivo.

4. T/F: siempre$\delta$ debe ser positivo.

Problemas

En los Ejercicios 5-11, acreditar el límite dado utilizando una$\epsilon -\delta$ prueba.

5. $\lim\limits_{x\to5}3-x+-2$

6. $\lim\limits_{x\to3}x^2-3=6$

7. $\lim\limits_{x\to4}x^2+x-5=15$

8. $\lim\limits_{x\to2}x^3-1=7$

9. $\lim\limits_{x\to2}5=5$

10. $\lim\limits_{x\to0}e^{2x}-1=0$

11. $\lim\limits_{x\to0}\sin x = 0$(Pista: utilizar el hecho de que$|\sin x |\le |x|,$ con igualdad sólo cuando$x=0$.)

1.3: Encontrar Límites Analíticamente

Términos y Conceptos

1. Explique con sus propias palabras, sin usar$ε-δ$ la formalidad, por qué$\lim\limits_{x\to c}b=b$.

2. Explique con sus propias palabras, sin usar$ε-δ$ la formalidad, por qué$\lim\limits_{x\to c}x=c$.

3. ¿Qué significa el texto cuando dice que el “comportamiento de ciertas funciones es 'agradable' en términos de límites”? ¿Qué, en particular, es “agradable”?

4. Esboce una gráfica que demuestre visualmente el Teorema de Squeeze

5. Se le da la siguiente información:

(a)$\lim\limits_{x\to1}f(x)=0$

b)$\lim\limits_{x\to1}g(x)=0$

c)$\lim\limits_{x\to1}f(x)/g(x) =2$

¿Qué se puede decir sobre los tamaños relativos de$f(x)$ y a$g(x)$ medida que x se acerca a 1?

Problemas

Usando:

\[\begin{align}\lim\limits_{x\to9}f(x)=6 \qquad \lim\limits_{x\to6}f(x)=9 \\ \lim\limits_{x\to9}g(x)=3 \qquad \lim\limits_{x\to6}g(x)=3 \end{align}\]

evaluar los límites dados en los Ejercicios 6-13, cuando sea posible. Si no es posible saberlo, declararlo así.

6. $\lim\limits_{x\to9}(f(x)+g(x))$

7. $\lim\limits_{x\to9}(3f(x)/g(x))$

8. $\lim\limits_{x\to9} \left ( \frac{f(x)-2g(x)}{g(x)}\right )$

9. $\lim\limits_{x\to6}\left (\frac{f(x)}{3-g(x)}\right )$

10. $\lim\limits_{x\to9}g(f(x))$

11. $\lim\limits_{x\to6}f(g(x))$

12. $\lim\limits_{x\to6}g(f(f(x)))$

13. $\lim\limits_{x\to6}f(x)g(x)-f^2(x)+g^2(x)$

Usando

\[\begin{align}\lim\limits_{x\to1}f(x)=2 \qquad \lim\limits_{x\to10}f(x)=1 \\ \lim\limits_{x\to1}g(x)=0 \qquad \lim\limits_{x\to10}g(x)=\pi \end{align}\]

evaluar los límites dados en los Ejercicios 14-17, cuando sea posible. Si no es posible saberlo, declararlo así.

14. $\lim\limits_{x\to1}f(x)^{g(x)}$

15. $\lim\limits_{x\to10}\cos (g(x))$

16. $\lim\limits_{x\to1}f(x)g(x)$

17. $\lim\limits_{x\to1}g(5f(x))$

En los Ejercicios 18-32, evaluar el límite dado.

18. $\lim\limits_{x\to3}x^2-3x+7$

19. $\lim\limits_{x\to\pi}\left ( \frac{x-3}{x+5}\right )^7$

20. $\lim\limits_{x\to\pi /4}\cos x \sin x$

21. $\lim\limits_{x\to 0}\ln x$

22. $\lim\limits_{x\to3}4^{{x^3}-8x}$

23. $\lim\limits_{x\to\pi/6}\csc x$

24. $\lim\limits_{x\to0}\ln (1+x)$

25. $\lim\limits_{x\to\pi}\frac{x^2+3x+5}{5x^2-2x-3}$

26. $\lim\limits_{x\to\pi}\frac{3x+1}{1-x}$

27. $\lim\limits_{x\to6}\frac{x^2-4x-12}{x^2-13x+42}$

28. $\lim\limits_{x\to0}\frac{x^2+2x}{x^2-2x}$

29. $\lim\limits_{x\to2}\frac{x^2+6x-16}{x^2-3x+2}$

30. $\lim\limits_{x\to2}\frac{x^2-5x-14}{x^2+10x+16}$

31. $\lim\limits_{x\to-2}\frac{x^2-5x-14}{x^2+10x+16}$

32. $\lim\limits_{x\to-1}\frac{x^2+9x+8}{x^2-6x-7}$\

Utilizar el Teorema de Squeeze en los Ejercicios 33-36, en su caso, para evaluar el límite dado.

33. $\lim\limits_{x\to0} x\sin \left (\frac{1}{x}\right )$

34. $\lim\limits_{x\to0}\sin x \cos \left ( \frac{1}{x^2}\right )$

35. $\lim\limits_{x\to1}f(x)$, donde$3x-2\le f(x)\le x^3.$

36. $\lim\limits_{x\to3+}f(x),$donde$6x-9\le f(x)\le x^2$ en [0,3].

Los ejercicios 37-40, desafían tu comprensión de los límites pero pueden ser evaluados utilizando los conocimientos adquiridos en esta sección.

37. $\lim\limits_{x\to0}\frac{\sin 3x}{x}$

38. $\lim\limits_{x\to0}\frac{\sin 5x}{8x}$

39. $\lim\limits_{x\to0}\frac{\ln (1+x)}{x}$

40. $\lim\limits_{x\to0}\frac{\sin x}{x}$, donde x se mide en grados, no en radianes.

1.4: Límites de un solo lado

Términos y Conceptos

1. ¿Cuáles son las tres formas en que un límite puede no existir?

2. T/F: Si$\lim\limits_{x\to1-}f(x)=5$, entonces$\lim\limits_{x\to1}f(x)=5$

3. T/F: Si$\lim\limits_{x\to1-}f(x)=5$, entonces$\lim\limits_{x\to1+}f(x)=5$

4. T/F: Si$\lim\limits_{x\to1}f(x)=5$, entonces$\lim\limits_{x\to1-}f(x)=5$

Problemas

En los Ejercicios 5-12, evalúe cada expresión utilizando la gráfica dada de$f(x)$.

5.
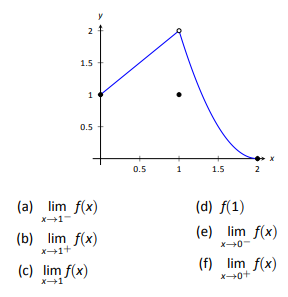
$clipboard_e4f5a8bce92d31a43cde475d21c7bbb8f.png$

6.
$146.PNG$

7.
$147.PNG$

8.
$148.PNG$

9.
$149.PNG$

10.
$1410.PNG$

11.
$1411.PNG$

12.
$1412.PNG$

En los Ejercicios 13-21, evaluar los límites dados de las funciones definidas por partes$f$.

13. $f(x) = \begin{cases} x+1 \quad &x\le 1\\ x^2-5 &x>1 \end{cases}$
(a)$\lim\limits_{x\to1^-}f(x) $
(b)$\lim\limits_{x\to0^+}f(x)$
(c)$\lim\limits_{x\to1}f(x) $
(d)$f(1)$

14. $f(x) = \begin{cases} 2x^2+5x-1 \quad &x<0 \\ \sin x &x\ge 0 \end{cases}$
(a)$\lim\limits_{x\to0^-}f(x)$
(b)$\lim\limits_{x\to0^+}f(x)$
(c)$\lim\limits_{x\to0}f(x) $
(d)$f(0)$

15. $f(x) = \begin{cases} x^-1 \quad &x<-1 \\ x^3+1 &-1\le x \le 1 \\ x^2+1 &x>1 \end{cases}$
(a)$\lim\limits_{x\to-1^-}f(x)$
(b)$\lim\limits_{x\to1^+}f(x)$
(c)$\lim\limits_{x\to-1}f(x) $
(d)$f(-1)$
(e)$\lim\limits_{x\to1^-}f(x)$
(f)$\lim\limits_{x\to1^+}f(x)$
(g)$\lim\limits_{x\to1}f(x)$
(h)$f(1)$

16. $f(x) = \begin{cases} \cos x \quad &x<\pi \\ \sin x &x\ge \pi \end{cases}$
(a)$\lim\limits_{x\to\pi^-}f(x)$
(b)$\lim\limits_{x\to\pi^+}f(x)$
(c)$\lim\limits_{x\to\pi}f(x) $
(d)$f(\pi)$

17. $f(x) = \begin{cases} 1-\cos ^2 x \quad &x<a \\ \sin^2 x &x\ge a \end{cases}$, donde$a$ es un número real.
(a)$\lim\limits_{x\to a^-}f(x)$
(b)$\lim\limits_{x\to a^+}f(x)$
(c)$\lim\limits_{x\to a}f(x) $
(d)$f(a)$

18. $f(x) = \begin{cases} x+1 \quad &x<1 \\ 1 &x=1 \\ x-1 &x>1 \end{cases}$
(a)$\lim\limits_{x\to1^-}f(x)$
(b)$\lim\limits_{x\to1^+}f(x)$
(c)$\lim\limits_{x\to1}f(x) $
(d)$f(1)$

19. $f(x) = \begin{cases} x^2 \quad &x<2 \\ x+1 &x=2 \\ -x^2+2x+4 &x>2 \end{cases}$
(a)$\lim\limits_{x\to2^-}f(x)$
(b)$\lim\limits_{x\to2^+}f(x)$
(c)$\lim\limits_{x\to2}f(x) $
(d)$f(2)$

20. $f(x) = \begin{cases} a(x-b)^2+c\quad &x<b \\ a(x-b)+c &x\ge b \end{cases}$, donde a, b y c son números reales.
(a)$\lim\limits_{x\to b^-}f(x)$
(b)$\lim\limits_{x\to b^+}f(x)$
(c)$\lim\limits_{x\to b}f(x) $
(d)$f(b)$

21. $f(x) = \begin{cases}\frac{|x|}{x} \quad &x\ne 0 \\ 0 &x= 0 \end{cases}$
(a)$\lim\limits_{x\to0^-}f(x)$
(b)$\lim\limits_{x\to0^+}f(x)$
(c)$\lim\limits_{x\to0}f(x) $
(d)$f(0)$

Revisar

22. Evaluar el límite:$\lim\limits_{x\to -1}\frac{x^2+5x+4}{x^2-3x-4}$

23. Evaluar el límite:$\lim\limits_{x\to -4}\frac{x^2-16}{x^2-4x-32}$

24. Evaluar el límite:$\lim\limits_{x\to -6}\frac{x^2-15x+54}{x^2-6x}$

25. Aproximar el límite numéricamente:$\lim\limits_{x\to 0.4}\frac{x^2-4.4x+1.6}{x^2-0.4x}$

26. Aproximar el límite numéricamente:$\lim\limits_{x\to 0.2}\frac{x^2+5.8x-1.2}{x^2-4.2x+0.8}$

1.5: Continuidad

Términos y Conceptos

1. En sus propias palabras, describa lo que significa que una función sea continua.

2. En sus propias palabras, describa lo que afirma el Teorema del Valor Intermedio.

3. ¿Qué es una “raíz” de una función?

4. Dadas funciones$f\text{ and }g$ en un intervalo$I$, ¿cómo se puede usar el Método de Bisección para encontrar un valor c dónde$f(c) = g(c)$?

5. T/F: Si$f$ se define en un intervalo abierto que contiene c, y$\lim\limits_{x\to c} f(x)$ existe, entonces$f$ es continuo en c.

6. T/F: Si$f$ es continuo en c, entonces$\lim\limits_{x\to c} f(x)$ existe

7. T/F: Si$f$ es continuo a c, entonces$\lim\limits_{x\to c^+} f(x)=f(c)$.

8. T/F: Si$f$ es continuo en [a, b], entonces$\lim\limits_{x\to a^-} f(x)=f(a)$.

9. T/F: Si f es continuo en [0, 1) y [1, 2), entonces$f$ es continuo en [0, 2).

10. T/F: La suma de funciones continuas también es continua.

Problemas

En los Ejercicios 11-17,$f$ se da una gráfica de una función junto con un valor$a$. Determinar si$f$ es continuo en$a$; si no lo es, indique por qué no lo es.

11. $a=1$
$1511.PNG$

12. $a=1$
$1512.PNG$

13. $a=1$
$1513.PNG$

14. $a=0$
$1514.PNG$

15. $a=1$
$1515.PNG$

16. $a=4$
$1516.PNG$

17.
(a)$a=-2$
(b)$a=0$
(c)$a=2$
$1517.PNG$

En los Ejercicios 18-21, determinar si$f$ es continuo a los valores indicados. Si no, explica por qué.

18. $f(x) = \begin{cases} 1 \quad &x=0\\ \frac{\sin x}{x} &x>0 \end{cases}$
a$x=0$
) b$x=\pi$

19. $f(x) = \begin{cases} x^3-x \quad &x<1\\ x-2 &x\ge 1 \end{cases}$
a$x=0$
) b$x=1$

20. $f(x) = \begin{cases} \frac{x^2+5x+4}{x^2 +3x+2} \quad &x\ne -1\\ 3 &x=-1 \end{cases}$
a$x=-1$
) b$x=10$

21. $f(x) = \begin{cases} \frac{x^2-64}{x^2-11x+24} \quad &x\ne 8\\ 5 &x=8 \end{cases}$
a$x=0$
) b$x=8$

En los Ejercicios 22-32, dé los intervalos en los que la función dada es continua.

22. $f(x)=x^2-3x+9$

23. $g(x) = \sqrt{x^2-4}$

24. $h(k) = \sqrt{1-k}+\sqrt{k+1}$

25. $f(t) = \sqrt{5t^2-30}$

26. $g(t) = \frac{1}{\sqrt{1-t^2}}$

27. $g(x) = \frac{1}{1+x^2}$

28. $f(x) = e^x$

29. $g(s) = \ln s $

30. $h(t) = \cos t$

31. $f(k) = \sqrt{1-e^k}$

32. $f(x) = \sin (e^x+x^2)$

33. Dejar$f$ ser continuo en [1,5] donde$f(1) = -2 \text{ and }f(5)=-10$. ¿$1<c<5$Existe un valor tal que$f(c)=-9$? ¿Por qué no?

34. Dejar$g$ ser continuo en [-3,7] donde$g(0)=0 \text{ and }g(2)=25$. ¿$-3<c<7$Existe un valor tal que$g(c)=15?$ por qué/¿por qué no?

35. Dejar$f$ ser continuo en [-1,1] donde$f(-1)=-10 \text{ and }f(1)=10$. ¿$-1<c<1$Existe un valor tal que$f(c)=11?$ por qué/¿por qué no?

36. Dejar$h$ ser continuo en [-1,1] donde$h(-1)=-10 \text{ and }h(1)=10$. ¿$-1<c<1$Existe un valor tal que$h(c)=0?$ por qué/¿por qué no?

En los Ejercicios 37-40, utilice el Método de Bisección para aproximar, con precisión a dos decimales, el valor de la raíz de la función dada en el intervalo dado.

37. $f(x) = x^2+2x-4\text{ on }[1,1.5]$.

38. $f(x) = \sin x -1/2\text{ on }[0.5,0.55]$.

39. $f(x) = e^x-2\text{ on }[0.65,0.7]$.

40. $f(x) = \cos x -\sin x \text{ on }[0.7,0.8]$.

Revisar

41. Vamos$f(x) = \begin{cases} x^2-5 \quad &x<5\\ 5x &x\ge 5 \end{cases}$.
(a)$\lim\limits_{x\to 5^-}f(x)$
(b)$\lim\limits_{x\to 5^+}f(x)$
(c)$\lim\limits_{x\to 5}f(x)$
(d)$f(5)$

42. Aproximar numéricamente los siguientes límites: a
$\lim\limits_{x\to 4/5^+}\frac{x^2-8.2x-7.2}{x^2+5.8x+4}$
) b$\lim\limits_{x\to 4/5^-}\frac{x^2-8.2x-7.2}{x^2+5.8x+4}$

43. Dar un ejemplo de función$f(x)$ para la que$\lim\limits_{x\to 0}f(x)$ no existe.

1.6: Límites que involucran el infinito

Términos y Conceptos

1. T/F: Si$\lim\limits_{x\to 5}f(x)=\infty$, entonces estamos declarando implícitamente que el límite existe.

2. T/F: Si$\lim\limits_{x\to \infty}f(x)=5$, entonces estamos declarando implícitamente que el límite existe.

3. T/F: Si$\lim\limits_{x\to 1^-}f(x)=-\infty$, entonces$\lim\limits_{x\to 1^+}f(x)=\infty$.

4. T/F: Si$\lim\limits_{x\to 5}f(x)=\infty$, entonces$f$ tiene una asíntota vertical en$x=5$.

5. T/F: no$\infty/0$ es una forma indeterminada.

6. Lista 5 formularios indeterminados.

7. Construir una función con una asíntota vertical en x = 5 y una asíntota horizontal en y = 5.

8. Vamos$\lim\limits_{x\to 7}f(x)=\infty$. Explicar cómo sabemos que$f$ es/no es continuo en$x=7$.

Problemas

En los Ejercicios 9-14, evalúe los límites dados utilizando la gráfica de la función.

9. $f(x) = \frac{1}{(x+1)^2}$
a$\lim\limits_{x\to -1^-}f(x)$
) b$\lim\limits_{x\to -1^+}f(x)$
$169.PNG$

10. $f(x) = \frac{1}{(x-3)(x-5)^2}$
a)$\lim\limits_{x\to 3^-}f(x)$
b$\lim\limits_{x\to 3^+}f(x)$
) c$\lim\limits_{x\to 3}f(x)$
) d$\lim\limits_{x\to 5^-}f(x)$
) e$\lim\limits_{x\to 5^+}f(x)$
) f$\lim\limits_{x\to 5}f(x)$
$1610.PNG$

11. $f(x) = \frac{1}{e^x+1}$
(a)$\lim\limits_{x\to -\infty}f(x)$
(b)$\lim\limits_{x\to \infty}f(x)$
(c)$\lim\limits_{x\to 0^-}f(x)$
(d)$\lim\limits_{x\to 0^+}f(x)$
$1611.PNG$

12. $f(x) = x^2\sin (\pi x)$
a$\lim\limits_{x\to -\infty}f(x)$
) b$\lim\limits_{x\to \infty}f(x)$
$1612.PNG$

13. $f(x)=\cos (x)$
a$\lim\limits_{x\to -\infty}f(x)$
) b$\lim\limits_{x\to \infty}f(x)$
$1613.PNG$

14. $f(x) = 2^x +10$
a$\lim\limits_{x\to -\infty}f(x)$
) b$\lim\limits_{x\to \infty}f(x)$
$1614.PNG$

En los Ejercicios 15 a 18, aproximar numéricamente los siguientes límites:
a $\lim\limits_{x\to 3^-}f(x)$
)$\lim\limits_{x\to 3^+}f(x)$
b) c$\lim\limits_{x\to 3}f(x)$

15. $f(x) = \frac{x^2-1}{x^2-x-6}$

16. $f(x) = \frac{x^2+5x-36}{x^3-5x^2+3x+9}$

17. $f(x) = \frac{x^2-11x+30}{x^3-4x^2-3x+18}$

18. $f(x) = \frac{x^2-9x+18}{x^2-x-6}$

En los Ejercicios 19-24, identificar las asíntotas horizontales y verticales, en su caso, de la función dada.

19. $f(x) = \frac{2x^2-2x-4}{x^2+x-20}$

20. $f(x) = \frac{-3x^2-9x-6}{5x^2-10x-15}$

21. $f(x) = \frac{x^2+2-12}{7x^3-14x^2-21x}$

22. $f(x) = \frac{x^2-9}{9x-9}$

23. $f(x) = \frac{x^2-9}{9x+27}$

24. $f(x) = \frac{x^2-1}{-x^2-1}$

En Ejercicios 25-28, evaluar el límite dado.

25. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{x-5}$

26. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{5-x}$

27. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{x^2-5}$

28. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{5-x^2}$

Revisar

29. Usa una$ε − δ$ prueba para demostrarlo$\lim\limits_{x\to 1}5x-2=3$.

30. Vamos$\lim\limits_{x\to 2}f(x)=3\text{ and }\lim\limits_{x\to 2}g(x)=-1$. Evaluar los siguientes límites.
(a)$\lim\limits_{x\to 2}(f+g)(x)$
(b)$\lim\limits_{x\to 2}(fg)(x)$
(c)$\lim\limits_{x\to 2}(f/g)(x)$
(d)$\lim\limits_{x\to 2}f(x)^{g(x)}$

31. Vamos$f(x) = \begin{cases}x^2-1 \qquad &x<3 \\ x+5 &x \ge 3 \end{cases}$. ¿Es$f$ continuo en todas partes?

32. Evaluar el límite:$\lim\limits_{x\to c}\ln x$.

Search

Text Color

Text Size

Margin Size

Font Type