4.1: Método de Newton

Última actualización
Guardar como PDF

Page ID: 111762

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En el capítulo 3 aprendimos cómo la primera y segunda derivadas de una función influyen en su gráfica. En este capítulo exploramos otras aplicaciones del derivado.

Resolver ecuaciones es una de las cosas más importantes que hacemos en matemáticas, sin embargo, estamos sorprendentemente limitados en lo que podemos resolver analíticamente. Por ejemplo, ecuaciones tan simples como$x^5+x+1=0$ o$\cos x =x$ no pueden ser resueltas por métodos algebraicos en términos de funciones familiares. Afortunadamente, existen métodos que nos pueden dar soluciones aproximadas a ecuaciones como estas. Estos métodos suelen dar una aproximación correcta a tantos decimales como queramos. En la Sección 1.5, aprendimos sobre el Método de Bisección. Esta sección se centra en otra técnica (que generalmente funciona más rápido), llamada Método de Newton.

El Método de Newton se construye alrededor de líneas tangentes. La idea principal es que si$x$ está suficientemente cerca de una raíz de$f(x)$, entonces la línea tangente a la gráfica$(x,f(x))$ cruzará el$x$ eje -en un punto más cercano a la raíz que$x$.

$alt$ $alt$ $alt$

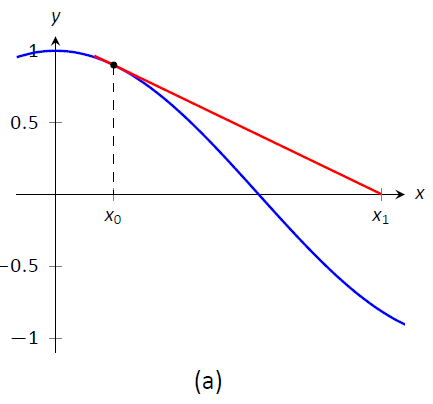
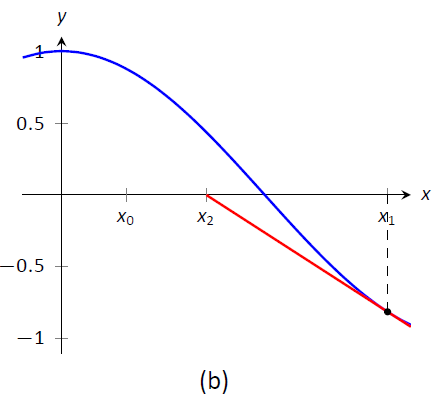
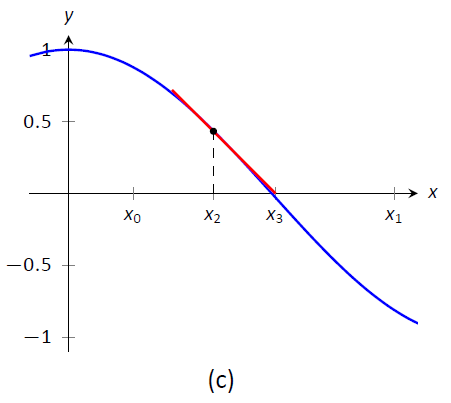
Figura$\PageIndex{1}$: Demostrando el concepto geométrico detrás del Método de Newton

Comenzamos el Método de Newton con una suposición inicial sobre aproximadamente dónde está la raíz. Llama a esto$x_0$. (Ver Figura$\PageIndex{1a}$.) Dibuje la línea tangente a la gráfica en$(x_0,f(x_0))$ y vea dónde se encuentra con el$x$ eje. Llama a este punto$x_1$. Luego repita el proceso — dibuja la línea tangente a la gráfica en$(x_1, f(x_1))$ y vea dónde se encuentra con el$x$ eje -eje. (Ver Figura$\PageIndex{1b}$.) Llama a este punto$x_2$. Repita nuevamente el proceso para obtener$x_3$,$x_4$, etc. Esta secuencia de puntos a menudo convergerá con bastante rapidez a una raíz de$f$.

Podemos utilizar este proceso geométrico para crear un proceso algebraico. Veamos cómo nos encontramos$x_1$. Empezamos con la línea tangente a la gráfica en$(x_0,f(x_0))$. La pendiente de esta línea tangente es$f'(x_0)$ y la ecuación de la línea es

$$y=f' (x_0) (x-x_0) +f (x_0).\]

Esta línea cruza el$x$ eje cuando$y=0$, y el$x$ valor —donde cruza es lo que llamamos$x_1$. Así que vamos$y=0$ y reemplázalo$x$ con$x_1$, dando la ecuación:

\[ 0 = f'(x_0)(x_1-x_0)+f(x_0).\]

Ahora resuelve para$x_1$:

\[x_1=x_0-\frac{f(x_0)}{f'(x_0)}.\]

Ya que repetimos los mismos proces geométricos para encontrar$x_2$$x_1$, tenemos

\[x_2=x_1-\frac{f(x_1)}{f'(x_1)}.\]

En general, dada una aproximación$x_n$, podemos encontrar la siguiente aproximación, de la$x_{n+1}$ siguiente manera:

\[x_{n+1} = x_{n} - \frac{f(x_{n})}{f'(x_{n})}.\]

Resumimos este proceso de la siguiente manera.

Idea Clave 5: Método de Newton

Dejar$f$ ser una función diferenciable en un intervalo$I$ con una raíz en$I$. Para aproximar el valor de la raíz, con precisión a los$d$ decimales:

Elija un valor$x_0$ como aproximación inicial de la raíz. (Esto se hace a menudo mirando una gráfica de$f$.)
Crea aproximaciones sucesivas iterativamente; dada una aproximación$x_n$, calcula la siguiente aproximación$x_{n+1}$ como $$x_ {n+1} = x_n -\ frac {f (x_n)} {f' (x_n)} . $$
Detenga las iteraciones cuando las aproximaciones sucesivas no difieran en los primeros$d$ lugares después del punto decimal.

Nota: El Método de Newton no es infalible. La secuencia de valores aproximados puede no converger, o puede converger tan lentamente que uno es “engañado” para pensar que una cierta aproximación es mejor de lo que realmente es. Estos temas serán discutidos al final de la sección.}

Practicemos el Método de Newton con un ejemplo concreto.

Ejemplo$\PageIndex{1}$: Using Newton's Method

Aproximar la raíz real de$x^3-x^2-1=0$, precisa a los primeros 3 lugares después del decimal, usando el Método de Newton y una aproximación inicial de$x_0=1$.}

Solución

Para comenzar, calculamos$f'(x)=3x^2-2x$. Después aplicamos el algoritmo del Método de Newton, esbozado en la Idea Clave 5.

\[\begin{align} x_1&=1-\frac{f(1)}{f'(1)}=1-\frac{1^3-1^2-1}{3\cdot 1^2-2\cdot 1}=2,\\ x_2&=2-\frac{f(2)}{f'(2)}=2-\frac{2^3-2^2-1}{3\cdot 2^2-2\cdot 2}=1.625,\\ x_3&=1.625-\frac{f(1.625)}{f'(1.625)} = 1.625-\frac{1.625^3-1.625^2-1}{3\cdot 1.625^2-2\cdot 1.625}\approx 1.48579. \\ x_4 &= 1.48579 - \frac{f(1.48579)}{f'(1.48579)} \approx 1.46596\\ x_5 &= 1.46596 - \frac{f(1.46596)}{f'(1.46596)} \approx 1.46557 \end{align}\]

Realizamos 5 iteraciones del Método de Newton para encontrar una raíz precisa a los primeros 3 lugares después del decimal; nuestra aproximación final es$1.465.$ El valor exacto de la raíz, a seis decimales, es$1.465571$; Resulta que nuestro$x_5$ es exacto a más de solo 3 decimales.

Una gráfica de$f(x)$ se da en la Figura$\PageIndex{2}$. Podemos ver en la gráfica que nuestra aproximación inicial de no$x_0=1$ era particularmente precisa; una conjetura más cercana habría sido$x_0=1.5$. Nuestra elección se basó en la facilidad de cálculo inicial, y muestra que el Método de Newton puede ser lo suficientemente robusto como para no tener que hacer una aproximación inicial muy precisa.

$alt$

Figura$\PageIndex{2}$: Una gráfica de$f(x) = x^3-x^2-1$ en Ejemplo$\PageIndex{1}$.

Podemos automatizar este proceso en una calculadora que tenga una clave Ans que devuelva el resultado del cálculo anterior. Comience por presionar$\texttt{1}$ y luego$\texttt{Enter}$. (Acabamos de entrar en nuestra suposición inicial,$x_0=1$.) Ahora cómpule

$$\ texttt {Ans} -\ frac {f (\ texttt {Ans})} {f' (\ texttt {Ans})}\]

ingresando lo siguiente y presionando repetidamente la$\texttt{Enter}$ tecla:

\[ \texttt{Ans}-(\texttt{Ans}^3-\texttt{Ans}^2-1)/(3*\texttt{Ans}^2-2*\texttt{Ans})\]

Cada vez que presionamos la tecla\ texttt {Enter}, estamos encontrando las aproximaciones sucesivas,$x_1$,$x_2$,\ dots, y cada una se acerca más a la raíz. De hecho, una vez que superamos más$x_7$ o menos, las aproximaciones no parecen estar cambiando. En realidad están cambiando, pero el cambio está lo suficientemente lejos a la derecha del punto decimal como para que no aparezca en la pantalla de la calculadora. Cuando esto sucede, podemos estar bastante seguros de que hemos encontrado una aproximación precisa.

El uso de una calculadora de esta manera simplifica los cálculos; muchas iteraciones se pueden calcular muy rápidamente.

Ejemplo$\PageIndex{2}$: Using Newton's Method to find where functions intersect

Utilice el Método de Newton para aproximar una solución a$\cos{x} = x$, con una precisión de 5 lugares después del decimal.

Solución

El Método de Newton proporciona un método de resolución$f(x) = 0$; no es (directamente) un método para resolver ecuaciones como$f(x) = g(x)$. Sin embargo, esto no es un problema; podemos reescribir esta última ecuación como$f(x) - g(x)=0$ y luego usar el Método de Newton.

Entonces reescribimos$\cos x=x$ como$\cos{x}-x=0$. Escrito de esta manera, estamos encontrando una raíz de$f(x)=\cos{x}-x$. Nosotros computamos$f'(x)=-\sin{x} - 1$. A continuación necesitamos un valor inicial,$x_0$. Considera Figura$\PageIndex{3}$, donde$f(x) = \cos x-x$ se grafica. Parece que$x_0=0.75$ está bastante cerca de la raíz, así que vamos a usar eso como nuestro$x_0$. (La figura también muestra las gráficas de$y=\cos x$ y$y=x$, dibujadas con líneas discontinuas. Observe cómo se cruzan al mismo$x$ valor que cuando$f(x) = 0$.)

$alt$

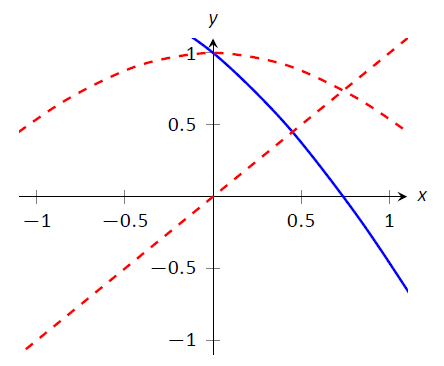
Figura$\PageIndex{3}$: Un gráfico de$f(x)=\cos x-x$ utilizado para encontrar una aproximación inicial de su raíz.

Ahora calculamos$x_1$,$x_2$, etc. La fórmula para$x_1$ es

\[x_1 = 0.75 - \frac{\cos(0.75)-0.75}{-\sin(0.75)-1}\approx 0.7391111388.\]

Aplica de nuevo el Método de Newton para encontrar$x_2$:

\[x_2 = 0.7391111388 - \frac{\cos(0.7391111388)-0.7391111388}{-\sin(0.7391111388)-1}\approx 0.7390851334.\]

Podemos continuar de esta manera, pero realmente lo mejor es automatizar este proceso. En una calculadora con una tecla Ans, comenzaríamos presionando 0.75, luego$\texttt{Enter}$, ingresando nuestra aproximación inicial. Luego entramos en:

\[\texttt{Ans - (cos(Ans)-Ans)/(-sin(Ans)-1).}\]

Al presionar repetidamente la$\texttt{Enter}$ tecla se obtienen aproximaciones sucesivas. Rápidamente encontramos:

\[ \begin{align} x_3 &= 0.7390851332\\ x_4 &= 0.7390851332. \end{align} \]

Nuestras aproximaciones$x_2$ y$x_3$ no difirieron por lo menos durante los primeros 5 lugares después del decimal, por lo que podríamos haber parado. Sin embargo, usar nuestra calculadora de la manera descrita es fácil, por lo que encontrar no$x_4$ fue difícil. Es interesante ver cómo encontramos una aproximación, exacta a tantos decimales como muestra nuestra calculadora, en tan solo 4 iteraciones.

Si sabes programar, puedes traducir el siguiente pseudocódigo a tu idioma favorito para realizar el cómputo en este problema.

$\texttt{x = .75}$
$\texttt{while true}$
$\texttt{oldx = x}$
$\texttt{x = x - (cos(x)-x)/(-sin(x)-1)}$
$\texttt{print x}$
$\texttt{if abs(x-oldx) < .0000000001}$
$\texttt{break}$

Este código calcula$x_1$,$x_2$, etc., almacenando cada resultado en la variable$\texttt{x}$. La aproximación previa se almacena en la variable$\texttt{oldx}$. Seguimos looping hasta que la diferencia entre dos aproximaciones sucesivas,$\texttt{abs(x-oldx)}$, sea menor que alguna tolerancia pequeña, en este caso,$\texttt{.0000000001}$.

Convergencia del método de Newton

¿Qué se debe usar para la conjetura inicial,$x_0$? Generalmente, cuanto más cerca de la raíz real esté la suposición inicial, mejor. No obstante, se deben evitar algunas conjeturas iniciales. Por ejemplo, consideremos Ejemplo$\PageIndex{1}$ donde buscábamos la raíz para$f(x) = x^3-x^2-1$. Elegir$x_0=0$ habría sido una elección particularmente mala. Considere Figura$\PageIndex{4}$, donde$f(x)$ se grafica junto con su línea tangente en$x=0$. Ya que$f'(0)=0$, la línea tangente es horizontal y no se cruza con el$x$ eje —. Gráficamente, vemos que el Método de Newton falla.

$alt$

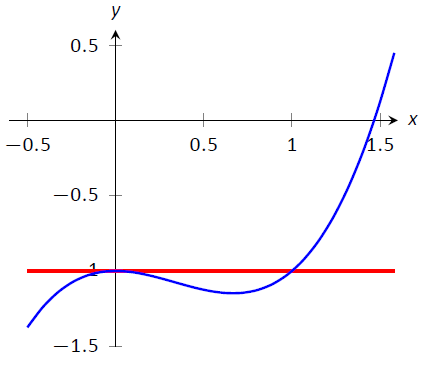
\ Figura$\PageIndex{4}$: Un gráfico de$f(x) = x^3-x^2-1$, que muestra por qué falla una aproximación inicial de$x_0=0$ con el Método de Newton.

También podemos ver analíticamente que falla. Desde

\[x_1 = 0 -\frac{f(0)}{f'(0)}\]

y$f'(0)=0$, vemos que no$x_1$ está bien definido.

Este problema también puede ocurrir si, por ejemplo, resulta que$f'(x_5)=0$. Ajustar la aproximación$x_0$ inicial en una cantidad muy pequeña probablemente solucionará el problema.

También es posible que el Método de Newton no converja mientras cada aproximación sucesiva está bien definida. Considere$f(x) = x^{1/3}$, como se muestra en la Figura$\PageIndex{5}$. Está claro que la raíz es$x=0$, pero aproximemos esto con$x_0=0.1$. La figura$\PageIndex{5a}$ muestra gráficamente el cálculo de$x_1$; observe cómo está más lejos de la raíz que$x_0$. Las cifras$\PageIndex{5b}$ y ($\PageIndex{5c}$) muestran el cálculo de$x_2$ y$x_3$, que están aún más lejos; nuestras sucesivas aproximaciones están empeorando. (Resulta que en este ejemplo particular, cada aproximación sucesiva está dos veces más lejos de la respuesta verdadera que la aproximación anterior.)

$alt$ $alt$ $alt$

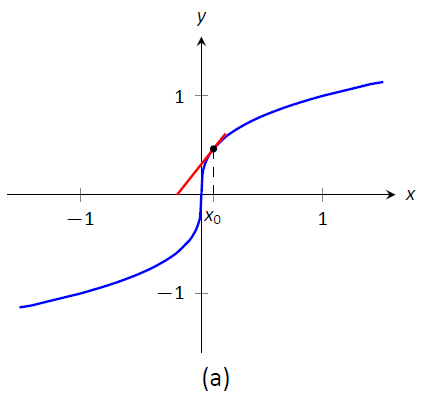
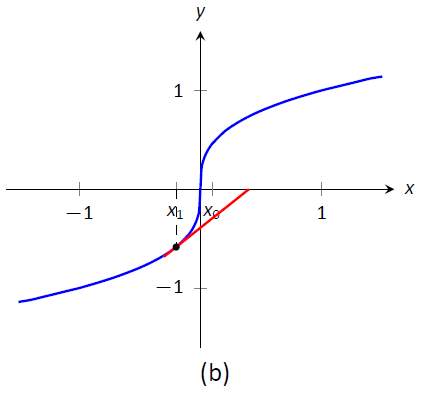
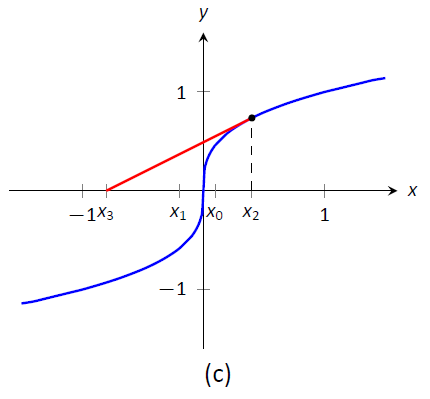
Figura$\PageIndex{5}$: El Método de Newton no logra encontrar una raíz de$f(x) = x^{1/3}$, independientemente de la elección de$x_0$.} \ label {fig:newt4}

No hay “solución” a este problema; el Método de Newton simplemente no funcionará y se debe usar otro método.

Si bien el Método de Newton no siempre funciona, sí funciona “la mayor parte del tiempo”, y generalmente es muy rápido. Una vez que las aproximaciones se acercan a la raíz, el Método de Newton puede hasta duplicar el número de decimales correctos con cada aproximación sucesiva. Un curso de Análisis Numérico introducirá al lector a métodos de búsqueda de raíces más iterativos, además de dar mayor detalle sobre las fortalezas y debilidades del Método de Newton.

Search

Text Color

Text Size

Margin Size

Font Type