8.7: Polinomios de Taylor

Considera una función$y=f(x)$ y un punto$\left(c,f(c)\right)$. La derivada,$f^\prime(c)$, da la velocidad instantánea de cambio de$f$ at$x=c$. De todas las líneas que pasan por el punto$\left(c,f(c)\right)$, la línea que mejor se$f$ aproxima en este punto es la línea tangente; es decir, la línea cuya pendiente (tasa de cambio) es$f^\prime(c)$.

En la Figura$\PageIndex{1}$, vemos una función$y=f(x)$ graficada. La tabla debajo de la gráfica muestra eso$f(0)=2$ y$f^\prime(0) = 1$; por lo tanto, la línea tangente a$f$ at$x=0$ es$p_1(x) = 1(x-0)+2 = x+2$. La línea tangente también se da en la figura. Tenga en cuenta que “cerca”$x=0$,$p_1(x) \approx f(x)$; es decir, la línea tangente se aproxima$f$ bien.

Figura$\PageIndex{1}$: Trazado$y=f(x)$ y una tabla de derivados de$f$ evaluados a 0.

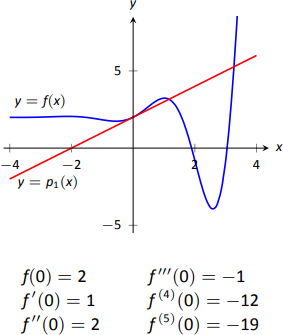
Una deficiencia de esta aproximación es que la línea tangente sólo coincide con la pendiente de$f$; no coincide, por ejemplo, con la concavidad de$f$. Podemos encontrar un polinomio,$p_2(x)$, que sí coincide con la concavidad sin mucha dificultad, aunque. El cuadro de la Figura 8.16 da la siguiente información:

$$f(0) = 2 \qquad f^\prime(0) = 1\qquad f^{\prime\prime}(0) = 2.$$

Por lo tanto, queremos que nuestro polinomio$p_2(x)$ tenga estas mismas propiedades. Es decir, necesitamos

$$p_2(0) = 2 \qquad p_2'(0) = 1 \qquad p_2''(0) = 2.$$

Esto es simplemente un problema de valor inicial. Podemos resolver esto usando las técnicas descritas por primera vez en la Sección 5.1. Para ser$p_2(x)$ lo más simple posible, asumiremos que no sólo$p_2''(0)=2$, sino eso$p_2''(x)=2$. Es decir, la segunda derivada de$p_2$ es constante.

Si$p_2''(x) = 2$, entonces$p_2'(x) = 2x+C$ para alguna constante$C$. Desde que lo hemos determinado$p_2'(0) = 1$, nos encontramos con eso$C=1$ y así$p_2'(x) = 2x+1$. Por último, podemos calcular$p_2(x) = x^2+x+C$. Usando nuestros valores iniciales, sabemos$p_2(0) = 2$ así$C=2.$ Concluimos que$p_2(x) = x^2+x+2.$ Esta función se grafica con$f$ en Figura$\PageIndex{2}$.

Figura$\PageIndex{2}$: Trazado$f$ (azul),$p_2$ (rojo) y$p_4$ (rojo claro).

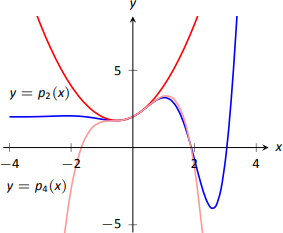
Podemos repetir este proceso de aproximación creando polinomios de mayor grado que coincidan con más de las derivadas de$f$ at$x=0$. En general, se$n$ puede crear un polinomio de grado para que coincida con las primeras$n$ derivadas de$f$. La figura$\PageIndex{2}$ también muestra$p_4(x)= -x^4/2-x^3/6+x^2+x+2$, cuyas primeras cuatro derivadas a 0 coinciden con las de$f$. (Usando la tabla de la Figura$\PageIndex{1}$, comience con$p_4^{(4)}(x)=-12$ y resuelva el problema relacionado con el valor inicial).

A medida que usamos cada vez más derivados, nuestra aproximación polinómica a$f$ mejora cada vez mejor. En este ejemplo, el intervalo en el que la aproximación es “buena” se hace cada vez más grande. La figura$\PageIndex{3}$ muestra$p_{13}(x)$; podemos afirmar visualmente que este polinomio se aproxima$f$ muy bien$[-2,3]$.

Figura$\PageIndex{3}$: Trazado$f$ y$p_{13}$.

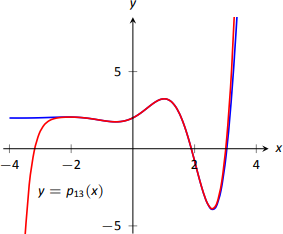
El polinomio no$p_{13}(x)$ es particularmente “agradable”. Es

$$p_{13} = \dfrac{16901x^{13}}{6227020800}+\dfrac{13x^{12}}{1209600}-\dfrac{1321x^{11}}{39916800}-\dfrac{779x^{10}}{1814400}-\dfrac{359x^9}{362880}+\dfrac{x^8}{240}+\dfrac{139x^7}{5040}+\dfrac{11 x^6}{360}-\dfrac{19x^5}{120}-\dfrac{x^4}{2}-\dfrac{x^3}{6}+x^2+x+2.$$

Los polinomios que hemos creado son ejemplos de polinomios de Taylor, que llevan el nombre del matemático británico Brook Taylor quien realizó importantes descubrimientos sobre tales funciones. Si bien creamos los polinomios Taylor anteriores resolviendo problemas de valor inicial, se puede demostrar que los polinomios Taylor siguen un patrón general que hace que su formación sea mucho más directa. Esto se describe en la siguiente definición.

Definición 38: Polinomios de Taylor y Polinomios de Maclaurin

Dejar$f$ ser una función cuyas primeras$n$ derivadas existen en$x=c$.

1. El polinomio Taylor de grado$n$ de$f$ at$x=c$ es $$p_n(x) = f(c) + f^\prime(c)(x-c) + \dfrac{f^{\prime\prime}(c)}{2!}(x-c)^2+\dfrac{f^{\prime\prime\prime}(c)}{3!}(x-c)^3+\cdots+\dfrac{f\,^{(n)}(c)}{n!}(x-c)^n.$$
2. Un caso especial del polinomio Taylor es el polinomio Maclaurin, donde$c=0$. Es decir, el polinomio Maclaurin de grado$n$ de$f$ es $$p_n(x) = f(0) + f^\prime(0)x + \dfrac{f^{\prime\prime}(0)}{2!}x^2+\dfrac{f^{\prime\prime\prime}(0)}{3!}x^3+\cdots+\dfrac{f\,^{(n)}(0)}{n!}x^n.$$

Practicaremos la creación de polinomios de Taylor y Maclaurin en los siguientes ejemplos.

Ejemplo$\PageIndex{1}$: Finding and using Maclaurin polynomials

1. Encuentra el polinomio$n^\text{th}$ Maclaurin para$f(x) = e^x$.
2. Utilizar$p_5(x)$ para aproximar el valor de$e$.

Solución

Figura$\PageIndex{4}$ Los derivados de$f(x) = e^x$ evaluados en$x=0$.

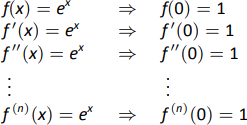
1. Comenzamos con la creación de una tabla de los derivados de$e^x$ evaluados en$x=0$. En este caso particular, esto es relativamente sencillo, como se muestra en la Figura 8.19.
   
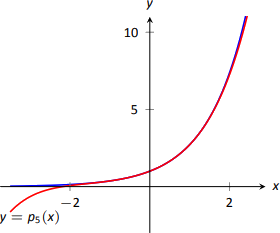
   Por la definición de la serie Maclaurin, tenemos $$\begin{align*}p_n(x) &= f(0) + f^\prime(0)x + \dfrac{f^{\prime\prime}(0)}{2!}x^2+\dfrac{f^{\prime\prime\prime}(0)}{3!}x^3+\cdots+\dfrac{f\,^n(0)}{n!}x^n\\&= 1+x+\dfrac{1}{2}x^2+\dfrac{1}{6}x^3 + \dfrac{1}{24}x^4 + \cdots + \dfrac{1}{n!}x^n.\end{align*}$$
2. Usando nuestra respuesta de la parte 1, tenemos $$p_5 = 1+x+\dfrac{1}{2}x^2+\dfrac{1}{6}x^3 + \dfrac{1}{24}x^4 + \dfrac{1}{120}x^5.$$ Para aproximar el valor de$e$, tenga en cuenta que$e = e^1 = f(1) \approx p_5(1).$ Es muy sencillo de evaluar$p_5(1)$: $$p_5(1) = 1+1+\dfrac12+\dfrac16+\dfrac1{24}+\dfrac1{120} = \dfrac{163}{60} \approx 2.71667.$$
   
   Una gráfica de$f(x)=e^x$ y$p_5(x)$ se da en la Figura$\PageIndex{5}$.

Figura$\PageIndex{5}$: Gráfica$f(x)=e^x$ y su polinomio Maclaurin de 5to grado$p_5(x)$.

Ejemplo$\PageIndex{2}$: Finding and using Taylor polynomials

1. Encuentra el polinomio de$n^\text{th}$ Taylor de$y=\ln x$ en$x=1$.
2. Utilizar$p_6(x)$ para aproximar el valor de$\ln 1.5$.
3. Utilizar$p_6(x)$ para aproximar el valor de$\ln 2$.

Solución

Figura$\PageIndex{6}$: Derivados de$\ln x$ evaluados en$x=1$.

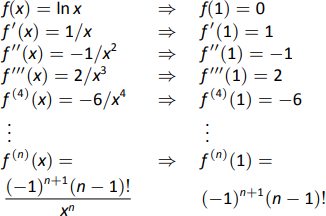
1. Comenzamos por crear una tabla de derivados de$\ln x$ evaluados en$x=1$. Si bien esto no es tan sencillo como lo fue en el ejemplo anterior, sí emerge un patrón, como se muestra en la Figura$\PageIndex{6}$.
   Usando la Definición 38, tenemos $$\begin{align*}p_n(x) &= f(c) + f^\prime(c)(x-c) + \dfrac{f^{\prime\prime}(c)}{2!}(x-c)^2+\dfrac{f^{\prime\prime\prime}(c)}{3!}(x-c)^3+\cdots+\dfrac{f\,^n(c)}{n!}(x-c)^n\\&= 0+(x-1)-\dfrac12(x-1)^2+\dfrac13(x-1)^3-\dfrac14(x-1)^4+\cdots+\dfrac{(-1)^{n+1}}{n}(x-1)^n.\end{align*}$$ Nota cómo los coeficientes de los$(x-1)$ términos resultan ser “agradables”.
2. Podemos calcular$p_6(x)$ usando nuestro trabajo anterior: $$p_6(x) = (x-1)-\dfrac12(x-1)^2+\dfrac13(x-1)^3-\dfrac14(x-1)^4+\dfrac15(x-1)^5-\dfrac16(x-1)^6.$$ Dado que$p_6(x)$ se aproxima$\ln x$ bien cerca$x=1$, aproximamos$\ln 1.5 \approx p_6(1.5)$: $$\begin{align*}p_6(1.5) &= (1.5-1)-\dfrac12(1.5-1)^2+\dfrac13(1.5-1)^3-\dfrac14(1.5-1)^4+\cdots \\&\cdots +\dfrac15(1.5-1)^5-\dfrac16(1.5-1)^6\\&=\dfrac{259}{640}\\&\approx 0.404688.\end{align*}$$ Esta es una buena aproximación ya que una calculadora muestra que$\ln 1.5 \approx 0.4055.$ Figura$\PageIndex{7}$ grafica$y=\ln x$ con$y=p_6(x)$. Eso lo podemos ver$\ln 1.5\approx p_6(1.5)$.

Figura$\PageIndex{7}$: Una gráfica de$y=\ln x$ y su polinomio Taylor de sexto grado en$x=1$.

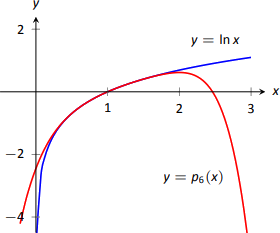
3. Nos aproximamos$\ln 2$ con$p_6(2)$: $$\begin{align*}p_6(2) &= (2-1)-\dfrac12(2-1)^2+\dfrac13(2-1)^3-\dfrac14(2-1)^4+\cdots \\&\cdots +\dfrac15(2-1)^5-\dfrac16(2-1)^6\\&= 1-\dfrac12+\dfrac13-\dfrac14+\dfrac15-\dfrac16 \\&= \dfrac{37}{60}\\ &\approx 0.616667.\end{align*}$$ Esta aproximación no es terriblemente impresionante: una calculadora de mano muestra que$\ln 2 \approx 0.693147.$ La gráfica de la Figura 8.22 muestra que$p_6(x)$ proporciona aproximaciones menos precisas de$\ln x$ como$x$ se acerca a 0 o 2.
   
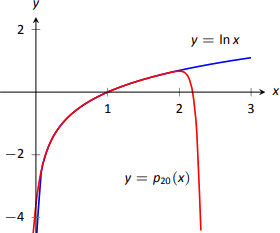
   Sorprendentemente, incluso el polinomio Taylor de 20$^\text{th}$ grados no logra aproximarse$\ln x$ para$x>2$, como se muestra en la Figura$\PageIndex{8}$. Pronto discutiremos por qué es esto.

Figura$\PageIndex{8}$: Una gráfica de$y=\ln x$ y su polinomio Taylor de 20 grados en$x=1$.

Los polinomios Taylor se utilizan para aproximar funciones principalmente$f(x)$ en dos situaciones:

1. Cuando$f(x)$ se sabe, pero quizás “difícil” de calcular directamente. Por ejemplo, podemos definir$y=\cos x$ como la relación de lados de un triángulo rectángulo (“adyacente sobre hipotenusa”) o con el círculo unitario. Sin embargo, ninguno de estos proporciona una forma conveniente de computación$\cos 2$. Un polinomio Taylor de grado suficientemente alto puede proporcionar un método razonable para calcular dichos valores usando solo operaciones generalmente cableadas en una computadora ($+$,$-$,$\times$ y$\div$).
2. Cuando no$f(x)$ se conoce, pero se conoce la información sobre sus derivados. Esto ocurre con más frecuencia de lo que uno podría pensar, especialmente en el estudio de ecuaciones diferenciales.

Aunque los polinomios Taylor podrían ser utilizados en calculadoras y computadoras para calcular valores de funciones trigonométricas, en la práctica generalmente no lo son. Se han desarrollado otros métodos más eficientes y precisos, como el algoritmo CORDIC.

En ambas situaciones, un dato crítico para tener es “¿Qué tan buena es mi aproximación?” Si usamos un polinomio de Taylor para calcular$\cos 2$, ¿cómo sabemos qué tan precisa es la aproximación?

Tuvimos el mismo problema a la hora de estudiar Integración Numérica. El teorema 43 proporcionó límites sobre el error al usar, digamos, la Regla de Simpson para aproximar una integral definida. Estos límites nos permitieron determinar que, por ejemplo, el uso de$10$ subintervalos proporcionaba una aproximación dentro$\pm .01$ del valor exacto. El siguiente teorema da límites similares para los polinomios de Taylor (y por lo tanto Maclaurin).

TEOREMA 76: TEOREMA DE TAYLOR

1. Dejar$f$ ser una función cuya$n+1^\text{th}$ derivada existe en un intervalo$I$ y let$c$ be in$I$. Entonces, para cada uno$x$ en$I$, existe$z_x$ entre$x$ y$c$ tal que
   $$f(x) = f(c) + f^\prime(c)(x-c) + \dfrac{f^\prime (c)}{2!}(x-c)^2+ \cdots +\dfrac{f\,^{(n)}(c)}{n!}(x-c)^n+R_n(x),$$
   donde$R_n(x) = \dfrac{f\,^{(n+1)}(z_x)}{(n+1)!}(x-c)^{(n+1)}.$
2. $\big|R_n(x)\big| \leq \dfrac{\max\left|\,f\,^{(n+1)}(z)\right|}{(n+1)!}\big|(x-c)^{(n+1)}\big|$

La primera parte del Teorema de Taylor afirma que$f(x) = p_n(x) + R_n(x)$, donde$p_n(x)$ está el polinomio del$n^\text{th}$ orden Taylor y$R_n(x)$ es el resto, o error, en la aproximación de Taylor. La segunda parte da límites sobre lo grande que puede ser ese error. Si la$(n+1)^\text{th}$ derivada es grande, el error puede ser grande; si$x$ está lejos de$c$, el error también puede ser grande. Sin embargo, el$(n+1)!$ término en el denominador tiende a asegurar que el error se hace menor a medida que$n$ aumenta.

El siguiente ejemplo calcula estimaciones de error para las aproximaciones de$\ln 1.5$ y$\ln 2$ realizadas en el Ejemplo 8.7.2.

Ejemplo$\PageIndex{3}$: Finding error bounds of a Taylor polynomial

Utilice el Teorema 76 para encontrar límites de error al aproximar$\ln 1.5$ y$\ln 2$ con$p_6(x)$, el polinomio Taylor de grado 6 de$f(x)=\ln x$ at$x=1$, según se calcula en el Ejemplo 8.7.2.

Solución

1. Comenzamos con la aproximación de$\ln 1.5$ con$p_6(1.5)$. El teorema hace referencia a un intervalo abierto$I$ que contiene tanto$x$ y$c$. Cuanto menor sea el intervalo que usemos mejor; nos dará una más precisa (¡y más pequeña!) aproximación del error. Dejamos$I = (0.9,1.6)$, ya que este intervalo contiene tanto$c=1$ y$x=1.5$.
   
   El teorema hace referencia$\max\big|f\,^{(n+1)}(z)\big|$. En nuestra situación, esto es preguntar “¿Qué tan grande puede ser la$7^\text{th}$ derivada de$y=\ln x$ estar en el intervalo$(0.9,1.6)$?” El séptimo derivado es$y = -6!/x^7$. El mayor valor en el que alcanza$I$ es de aproximadamente 1506. Así podemos encuadernar el error como: $$\begin{align*}\big|R_6(1.5)\big| &\leq \dfrac{\max\big|f\,^{(7)}(z)\big|}{7!}\big|(1.5-1)^7\big|\\&\leq \dfrac{1506}{5040}\cdot\dfrac1{2^7}\\&\approx 0.0023.\end{align*}$$
   
   Calculamos$p_6(1.5) = 0.404688$; usando una calculadora, nos encontramos$\ln 1.5 \approx 0.405465$, por lo que el error real es sobre$0.000778$, que es menor que nuestro límite de$0.0023$. Esto afirma el teorema de Taylor; el teorema afirma que nuestra aproximación estaría dentro de aproximadamente 2 milésimas del valor real, mientras que la aproximación en realidad estaba más cerca.
   
2. Nuevamente encontramos un intervalo$I$ que contiene ambos$c=1$ y$x=2$; elegimos$I = (0.9,2.1)$. El valor máximo de la séptima derivada de$f$ en este intervalo es de nuevo alrededor de 1506 (ya que los valores más grandes se acercan$x=0.9$). Por lo tanto, $$\begin{align*}\big| R_6(2)\big| &\leq \dfrac{\max\big|f\,^{(7)}(z)\big|}{7!}\big|(2-1)^7\big|\\&\leq \dfrac{1506}{5040}\cdot1^7\\&\approx 0.30.\end{align*}$$
   
   esta encuadernación no es tan buena como antes. El uso del polinomio Taylor grado 6 en nos$x =1$ llevará dentro de 0.3 de la respuesta correcta. Como$p_6(2)\approx 0.61667$, nuestra estimación de errores garantiza que el valor real de$\ln 2$ está en algún lugar entre$0.31667$ y$0.91667$. Estos límites no son particularmente útiles.
   
   En realidad, nuestra aproximación sólo estuvo apagada en aproximadamente 0.07. No obstante, nos estamos aproximando ostensiblemente porque no conocemos la respuesta real. Para estar seguros de que tenemos una buena aproximación, tendríamos que recurrir a utilizar un polinomio de mayor grado.

Volvemos a practicar. Esta vez, utilizamos el teorema de Taylor para encontrar$n$ que garantiza que nuestra aproximación está dentro de cierta cantidad.

Ejemplo$\PageIndex{4}$: Finding sufficiently accurate Taylor polynomials

Encuentra$n$ tal que el polinomio$n^\text{th}$ Taylor de$f(x)=\cos x$ at$x=0$ se aproxime$\cos 2$ al interior$0.001$ de la respuesta real. ¿Qué es$p_n(2)$?

Solución

Siguiendo el teorema de Taylor, necesitamos límites en el tamaño de los derivados de$f(x)=\cos x$. En el caso de esta función trigonométrica, esto es fácil. Todos los derivados del coseno son$\pm \sin x$ o$\pm \cos x$. En todos los casos, estas funciones nunca son mayores de 1 en valor absoluto. Queremos que el error sea menor que$0.001$. Para encontrar lo apropiado$n$, considere las siguientes desigualdades:

\ [\ begin {alinear*}
\ dfrac {\ max\ big|f\, ^ {(n+1)} (z)\ big|} {(n+1)!} \ big| (2-0) ^ {(n+1)}\ big| &\ leq 0.001\\
\ dfrac1 {(n+1)!} \ cdot2^ {(n+1)} &\ leq 0.001
\ final {alinear*}\]

Encontramos una$n$ que satisface esta última desigualdad con prueba y error. Cuando$n=8$, tenemos$\dfrac{2^{8+1}}{(8+1)!} \approx 0.0014$; cuando$n=9$, tenemos$\dfrac{2^{9+1}}{(9+1)!} \approx 0.000282 <0.001$. Así queremos aproximarnos$\cos 2$ con$p_9(2)$. \\

Ahora nos propusimos calcular$p_9(x)$. Nuevamente necesitamos una tabla de los derivados de$f(x)=\cos x$ evaluados en$x=0$. Una tabla de estos valores se da en la Figura$\PageIndex{8}$.

Figura$\PageIndex{9}$: Una tabla de los derivados de$f(x)=cos x$ evaluados at$x=0$.

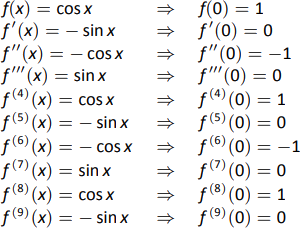
Observe cómo las derivadas, evaluadas en$x=0$, siguen un cierto patrón. Todos los poderes impares de$x$ en el polinomio Taylor desaparecerán ya que su coeficiente es 0. Si bien nuestros límites de error establecen que necesitamos$p_9(x)$, nuestro trabajo demuestra que esto será lo mismo que$p_8(x)$.

Como estamos formando nuestro polinomio en$x=0$, estamos creando un polinomio Maclaurin, y:

\ [\ begin {align*}
p_8 (x) &= f (0) + f^\ prime (0) x +\ dfrac {f^ {\ prime\ prime} (0)} {2!} x^2 +\ dfrac {f^ {\ prime\ prime\ prime} (0)} {3!} x^3 +\ cdots +\ dfrac {f\, ^ {(8)}} {8!} x^8\\
&= 1-\ dfrac {1} {2!} x^2+\ dfrac {1} {4!} x^4-\ dfrac {1} {6!} x^6+\ dfrac {1} {8!} x^8
\ final {alinear*}\]

Finalmente aproximamos$\cos 2$:

$$\cos 2 \approx p_8(2) = -\dfrac{131}{315} \approx -0.41587. \nonumber$$

Nuestro límite de error garantiza que esta aproximación está dentro$0.001$ de la respuesta correcta. La tecnología nos muestra que nuestra aproximación está realmente dentro$0.0003$ de la respuesta correcta.

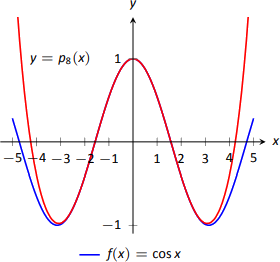
La figura$\PageIndex{10}$ muestra una gráfica de$y=p_8(x)$ y$y=\cos x$. Tenga en cuenta lo bien que coinciden las dos funciones$(-\pi,\pi)$.

Figura$\PageIndex{10}$: Una gráfica del polinomio Maclaurin$f(x)=cos x$ y su grado 8.

Ejemplo$\PageIndex{5}$: Finding and using Taylor polynomials

1. Encuentra el grado 4 Polinomio Taylor,$p_4(x)$, para$f(x)=\sqrt{x}$ en$x=4.$
2. Úselo$p_4(x)$ para aproximar$\sqrt{3}$.
3. Encuentra límites en el error al aproximar$\sqrt{3}$ con$p_4(3)$.

Solución

Figura$\PageIndex{11}$: Una tabla de los derivados de$f(x)=\sqrt{x}$ evaluados at$x=4$.

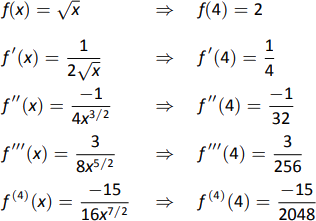
1. Comenzamos evaluando los derivados de$f$ at$x=4$. Esto se hace en la Figura$\PageIndex{11}$. Estos valores nos permiten formar el polinomio Taylor$p_4(x)$: $$p_4(x) = 2 + \dfrac14(x-4) +\dfrac{-1/32}{2!}(x-4)^2+\dfrac{3/256}{3!}(x-4)^3+\dfrac{-15/2048}{4!}(x-4)^4.$$
2. Como$p_4(x) \approx \sqrt{x}$ cerca$x=4$, aproximamos$\sqrt{3}$ con$p_4(3) = 1.73212$.
3. Para encontrar un límite en el error, necesitamos un intervalo abierto que contenga$x=3$ y$x=4$. Nos fijamos$I = (2.9,4.1)$. El mayor valor de la quinta derivada de$f(x)=\sqrt{x}$ tomas en este intervalo está cerca$x=2.9$, a aproximadamente$0.0273$. Así $$\big|R_4(3)\big| \leq \dfrac{0.0273}{5!}\big|(3-4)^5\big| \approx 0.00023.$$
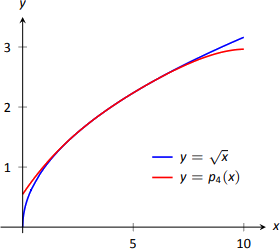
   Esto muestra que nuestra aproximación es precisa al menos a los primeros 2 lugares después del decimal. (Resulta que nuestra aproximación es en realidad exacta a 4 lugares después del decimal). Una gráfica de$f(x)=\sqrt x$ y$p_4(x)$ se da en la Figura$\PageIndex{12}$. Observe cómo las dos funciones son casi indistinguibles en$(2,7)$.

Figura$\PageIndex{12}$: Una gráfica de$f(x)=\sqrt{x}$ y su polinomio Taylor grado 4 en$x=4$.

Nuestro último ejemplo da una breve introducción al uso de polinomios de Taylor para resolver ecuaciones diferenciales.

Ejemplo$\PageIndex{6}$: Approximating an unknown function

Se$y=f(x)$ desconoce una función salvo por los dos hechos siguientes.

1. $y(0) = f(0) = 1$, y
2. $y^\prime= y^2$

(Este segundo hecho dice que asombrosamente, ¡la derivada de la función es en realidad la función al cuadrado!)

Encuentra el grado 3 Polinomio Maclaurin$p_3(x)$ de$y=f(x)$.

Solución

Uno podría pensar inicialmente que no se da suficiente información para encontrar$p_3(x)$. Sin embargo, tenga en cuenta cómo el segundo hecho anterior realmente nos permite saber qué$y^\prime(0)$ es:

$$y^\prime = y^2 \Rightarrow y^\prime(0) = y^2(0). \nonumber$$

Ya que$y(0) = 1$, concluimos que$y^\prime(0) = 1$.

Ahora encontramos información sobre$y^{\prime\prime}$. Empezando por$y^\prime=y^2$, tomar derivados de ambos lados, con respecto a$x$. Eso significa que debemos usar la diferenciación implícita.

\ [\ begin {align*}
y^\ prime &= y^2\
\ dfrac {d} {dx}\ left (y^\ prime\ right) &=\ dfrac {d} {dx}\ left (y^2\ right)\\
y^ {\ prime\ prime} &= 2y\ cdot y^\ prime. \\
\ text {Ahora evalúa ambos lados en$x=0$:} &\\
y^ {\ prime\ prime} (0) &= 2y (0)\ cdot y^\ prime (0)\\
y^ {\ prime\ prime} (0) &= 2
\ end {align*}\]

Repetimos esto una vez más para encontrar$y^{\prime\prime\prime}(0)$. Nuevamente utilizamos la diferenciación implícita; esta vez también se requiere la Regla del Producto.

\ [\ begin {align*}
\ dfrac {d} {dx}\ left (y^ {\ prime\ prime}\ derecha) &=\ dfrac {d} {dx}\ izquierda (2yy^\ prime\ derecha)\\
y^ {\ prime\ prime\ prime} &= 2y^\ prime\ cdot y^\ prime + 2y\ cdot y^ {prime\ prime\}. \\
\ text {Ahora evalúa ambos lados en$x=0$:} &\\
y^ {\ prime\ prime\ prime} (0) &= 2y^\ prime (0) ^2 + 2y (0) y^ {\ prime\ prime} (0)\\
y^ {\ prime\ prime\ prime} (0) &= 2+4=6
\ end {align*}\]

En resumen, tenemos:

$$y(0) = 1 \qquad y^\prime(0) = 1 \qquad y^{\prime\prime}(0) = 2 \qquad y^{\prime\prime\prime}(0) = 6. \nonumber$$

Ahora podemos formar$p_3(x)$:

\ [\ begin {alinear*}
p_3 (x) &= 1 + x +\ dfrac {2} {2!} x^2 +\ dfrac {6} {3!} x^3\\
&= 1+x+x^2+x^3.
\ end {alinear*}\]

Figura$\PageIndex{13}$: Gráfica de$y=-1/(x-1)$ y$y=p_a(x)$ a partir del Ejemplo 8.7.6.

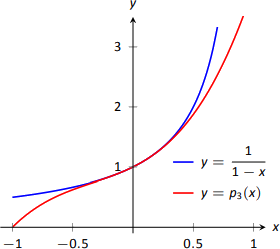
Resulta que la ecuación diferencial con la que empezamos,$y^\prime=y^2$, donde$y(0)=1$, se puede resolver sin demasiada dificultad:$y = \dfrac{1}{1-x}$. La Figura 8.28 muestra esta función trazada con$p_3(x)$. Tenga en cuenta lo similares que están cerca$x=0$.

Está más allá del alcance de este texto perseguir el análisis de errores cuando se utilizan polinomios de Taylor para aproximar soluciones a ecuaciones diferenciales. Este tema a menudo se aborda en cursos introductorios de Ecuaciones Diferenciales y generalmente se trata en profundidad en los cursos de Análisis Numérico. Tal análisis es muy importante; se necesita saber qué tan buena es su aproximación. Exploramos este ejemplo simplemente para demostrar la utilidad de los polinomios de Taylor.

La mayor parte de este capítulo se ha dedicado al estudio de series infinitas. Esta sección ha dado un paso atrás en este estudio, centrándose en cambio en la suma finita de términos. En la siguiente sección, exploramos Taylor Series, donde representamos una función con una serie infinita.

Colaboradores y Atribuciones

• Template:ContribApexCalc