Saltar al contenido principal
LibreTexts Español

Unidad 6: Revisión

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    117866

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Ahora practicarás todas las habilidades que aprendiste en el Libro 6. Puedes usar esto como revisión para tu prueba final.

    Si no recuerdas cómo hacer una pregunta, vuelve a la lección sobre este tema para refrescar tu memoria. La unidad y el tema de donde proviene cada pregunta se enumera junto a la pregunta.

     

    Nota Rápida

    Ejemplo: 1A significa Unidad 1, Tema A

    Unidad 1

    1-A

    1. Escribe las proporciones solicitadas.
      1. Lillian viajó en bicicleta durante 6 horas, y recorrió un total de 45 km. ¿Cuál es la relación de kilómetros a horas?
      2. En la terminal del ferry se alinearon novecientos autos. 300 mil autos subieron a la siguiente navegación. Escribe una relación de cuántos autos quedaron atrás y cuántos autos llegaron en la primera navegación.

    1-B

    2. Simplifica estas proporciones.

    1. \(9:12\)
    2. \(50:5\)
    3. \(56:7\)
    4. \(100:120\)

    3. Escribe las siguientes proporciones como tarifas.

    a. 110 kilómetros a 2 horas

    b. 9 tazas de harina a 3 cucharadas de levadura

    c. 240,000 personas a 300 kilómetros cuadrados

    1-C

    4. Resuelve estas proporciones.

    1. \(1:3=N:12\)
    2. \(25:N=20:4\)
    3. \(N:49=14:98\)
    4. \(412:6=N:3.6\)
    5. La dosis de jarabe para la tos es de 20 mililitros por cada 100 libras de peso corporal. ¿Cuánto se le debe dar a un niño de 34 libras? Redondear al mililitro más cercano.

    Unidad 2

    2-A

    5. Escribe estos porcentajes usando números y el signo de porcentaje.

    1. Setenta y dos por ciento
    2. Tres cuartas partes por ciento
    3. Ciento dos por ciento

    6. Escribe estos porcentajes en palabras.

    1. \(12\%\)
    2. \(\dfrac{1}{5}\%\)

    7. Cambiar los porcentajes a decimales equivalentes.

    1. \(17\%\)
    2. \(98\dfrrac{1}{2}\%\)
    3. \(\dfrac{1}{3}\%\)

    8. Escribe los decimales como porcentajes.

    1. 0.45
    2. 4.75
    3. 0.099

    9. Cambiar cada porcentaje a una fracción común equivalente. Poner la fracción en términos más bajos.

    1. \(33\dfrac{1}{3}\%\)
    2. \(14\%\)
    3. \(250\%\)

    10. Escribe el porcentaje equivalente

    1. \(\dfrac{1}{5}\)
    2. \(\dfrac{2}{3}\)
    3. \(\dfrac{1}{4}\)

    Unidad 3

    3-A

    11. Encuentra las respuestas. (Porcentaje expreso redondeado al décimo más cercano, dinero al centavo más cercano y decimales a la milésima más cercana. Por favor, muestre todo su trabajo. Proporción de uso.)

    1. \(13\% \text{ of } 52 =\)
    2. \(\dfrac{9}{10}\% \text{ of } 2,400\)es.
    3. ¿Qué es\(135\%\) de\(1,080\)?

    12. Resolver estos problemas. Asegúrate de mostrar todo tu trabajo.

    1. Marianne está renovando su cocina, y está ordenando todo en su ferretería local. Ella está recibiendo un fregadero por 204.79 dólares, un lavaplatos por $524.95, un mostrador por $949.99, pisos por $719.95 y una nevera por $579.49.
      1. Calcular el HST (12%).
      2. Calcular el costo total, incluyendo los impuestos.
    2. Shane vendió una casa por $340,500.00 para un cliente. Obtuvo 6% de comisión. ¿Cuánto dinero ganó Shane?
    3. Un asiento de amor tiene un precio original de $904.00, se ofrece con 45% de descuento. ¿Cuál es el precio de descuento?
    4. Calcula el costo total en dólares canadienses de esta compra realizada en Estados Unidos. Asumir $1.00 Canadiense = $0.92 US
      Clothes—Precio total en $US=$317.98ropa—Precio total en $US=$317.98.
      1. Precio en dólares canadienses
      2. Deber a 13.5%
      3. Total del valor canadiense + arancel
      4. HST (12%) sobre valor canadiense + arancel
      5. Costo total en dólares canadienses

    Unidad 4

    4-A

    13. Encuentra las respuestas.

    1. ¿34 es qué porcentaje de 85?
    2. ¿Qué% de 150 es 114?
    3. ¿33% de qué número es 60?
    4. ¿32 es 20% de qué número?
    5. ¿75% de qué número es 675?
    6. 3.75 es 1¼% de?

    14. Resolver estos problemas. Asegúrate de mostrar todo tu trabajo.

    1. Una impresora tiene un precio de 399 dólares. Se marca 30% de descuento.
      1. ¿Cuál es el precio de venta de la impresora?
      2. ¿Cuál es el costo de esta impresora con HST (12%)?
    2. El Servicio de Bomberos y Rescate de Vancouver cuenta con 797 uniformados, alrededor del 0.8% son mujeres. Acerca de cuántas mujeres están de uniforme en el Servicio de Bomberos y Rescate de Vancouver?
    3. Jake es un vendedor de computadoras. Recibe un salario mensual de $1,055 más 15% en todas sus ventas superiores a $5,500. ¿Cuál era su ingreso mensual total si sus ventas fueran de
      12.400 dólares en un mes?
    4. El cerro de esquí local vendió 3,800 pases de temporada en 2009. Las ventas de 2010 bajaron 10.5%. Encuentra el número de pases de temporada vendidos en 2010.

    Unidad 5

    5-A

    15. Gráfico de líneas.

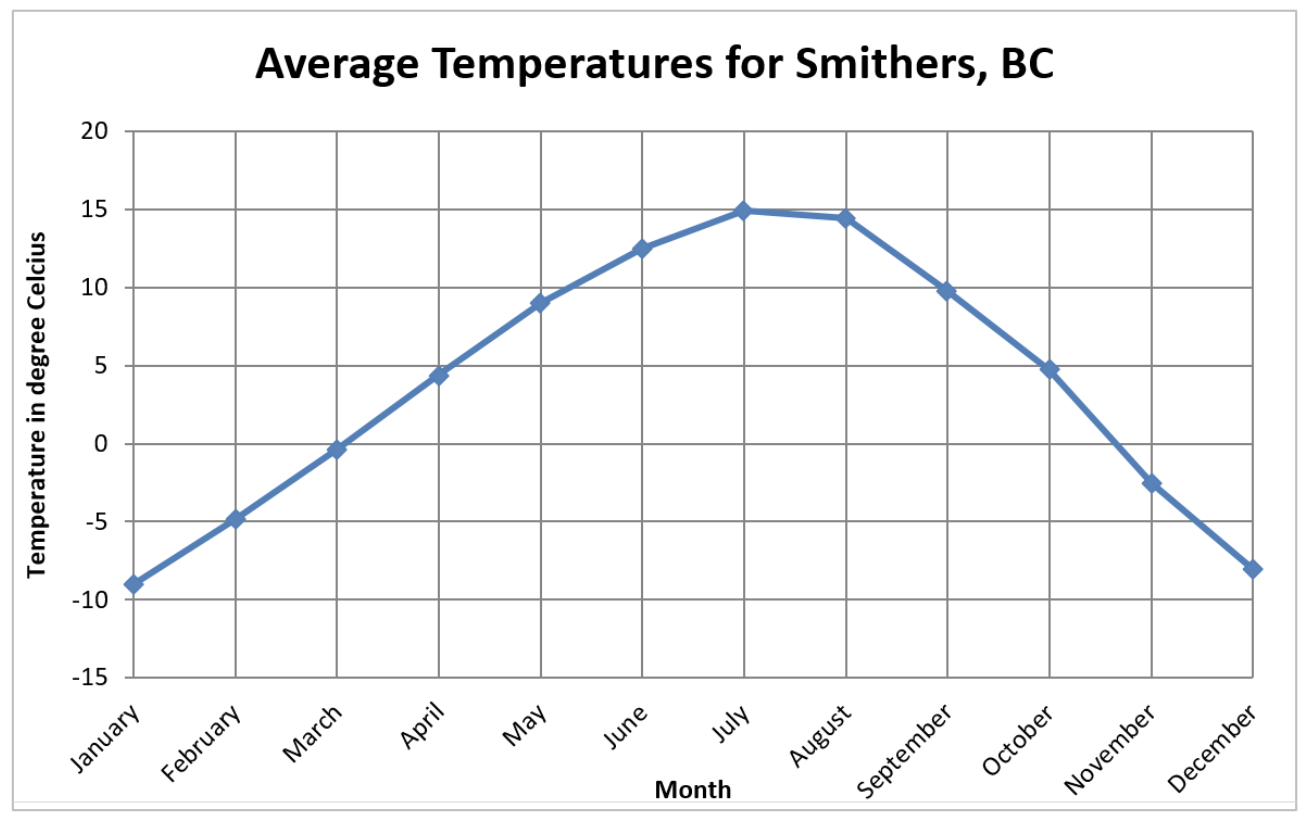
    Screen Shot 2022-05-04 a las 7.53.28 PM.png

    1. ¿Cuál mes tiene la temperatura más alta en Smithers?
    2. ¿Cuál mes tiene la temperatura más baja en Smithers?
    3. Entre los meses de enero a julio, ¿hay un aumento o disminución de la temperatura?
    4. ¿Cuál es la diferencia entre la temperatura mensual para agosto y la temperatura mensual para octubre?
    5. ¿Cuál es la tendencia de la temperatura en Smithers?

    5-B

    16. Gráfico de barras.

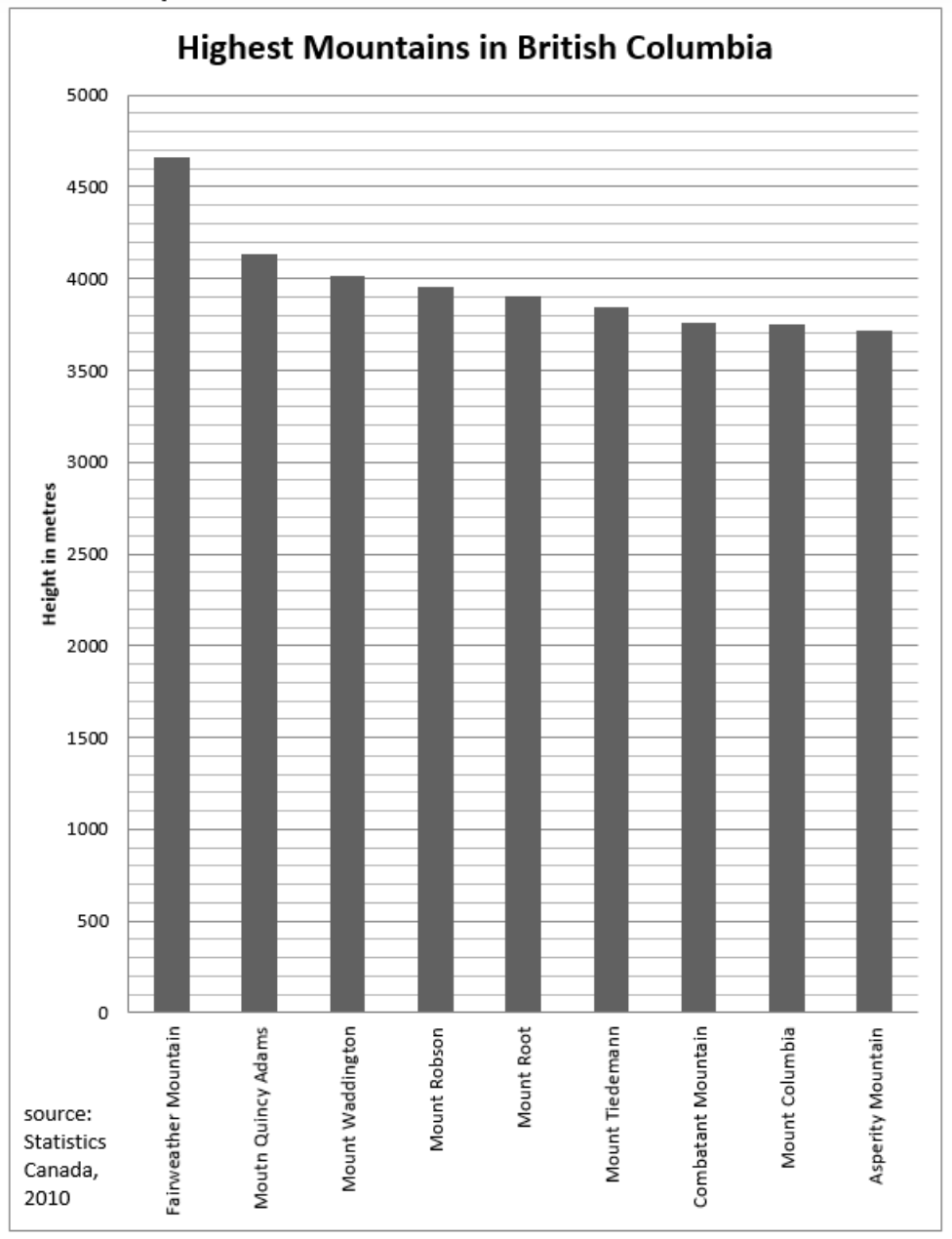
    Screen Shot 2022-05-04 a las 7.55.13 PM.png

    1. ¿Cuál es la altura de la montaña más alta de BC?
    2. ¿Cuántas montañas tienen más de 4.000 metros y menos de 5.000 metros de altura?
    3. ¿Cuáles dos montañas en esta tabla son muy similares en altura?
    4. ¿Cuál es la diferencia (aproximadamente) en altura entre Fairweather Mountain y Asperity Mountain?

    5-C

    17. Gráfico de imagen.

    Screen Shot 2022-05-04 a las 7.56.19 PM.png

    1. ¿Cuántos alumnos del segundo grado van en bicicleta a la escuela?
    2. ¿Qué clases tienen más ciclistas?
    3. ¿Qué clase tiene menos ciclistas?
    4. ¿Cuántos ciclistas más hay en 7º grado que en kindergarten?
    5. ¿Cuántos alumnos andan en bicicleta en total?
    6. ¿Qué porcentaje de las bicicletas escolares cada día?

    5-D

    18. Gráfica circular.

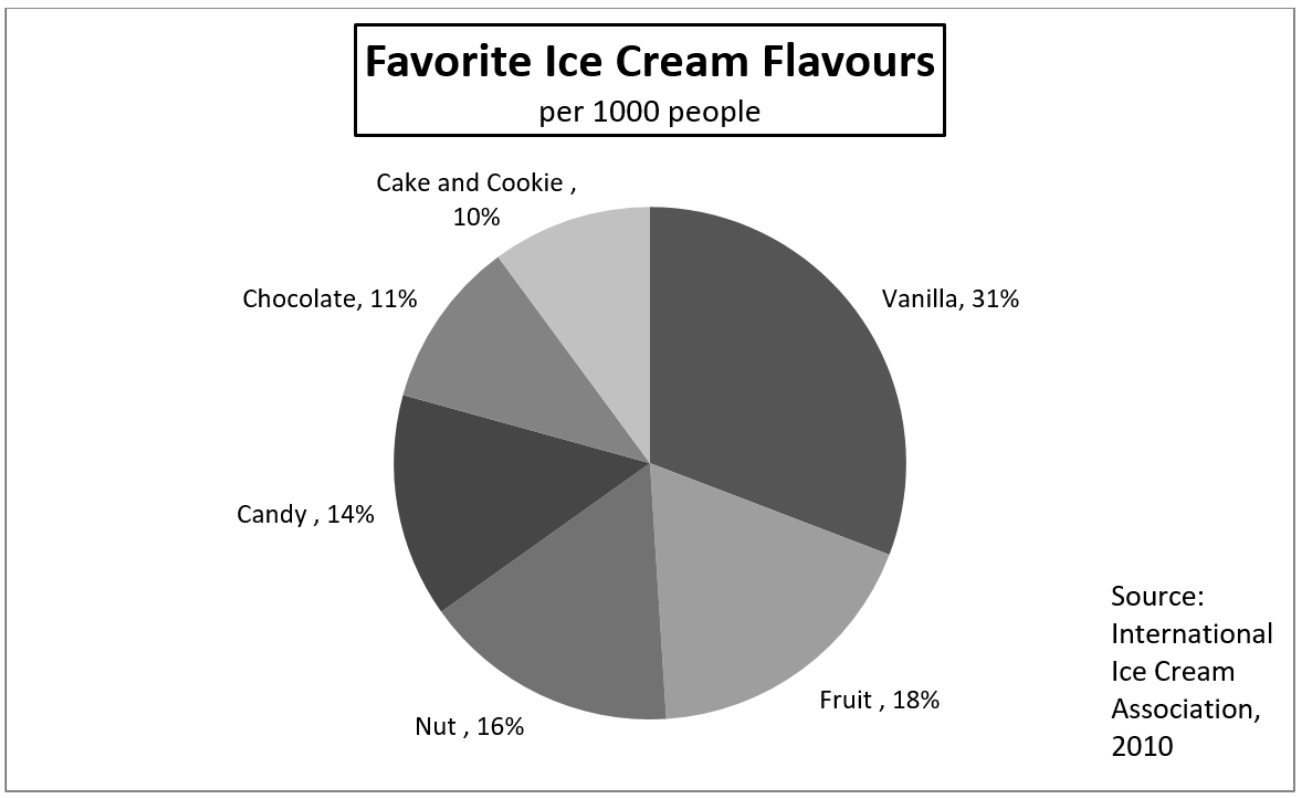
    Screen Shot 2022-05-04 a las 7.57.22 PM.png

    1. ¿Cuál es el sabor de helado más favorito?
    2. ¿Cuál es el sabor de helado que menos le gusta?
    3. ¿A cuántas personas (de 1,000) les gusta el helado con sabor a frutas?
    4. ¿Qué porcentaje de gente le gusta la vainilla sobre el chocolate?

     

    Respuestas a Book 6 Review

      1. \(45:6\)
      2. \(600:300\)
      1. \(3:4\)
      2. \(10:1\)
      3. \(8:1\)
      4. \(5:6\)
      1. \(55  \rm km/hr\)o\(55 \rm km:1 \rm hr\)
      2. 3 tazas de harina por 1 cucharada de levadura
      3. 800 personas a 1 km cuadrados
      1. 4
      2. 5
      3. 7
      4. 2.7
      5. 7 mL
      1. \(72\%\)
      2. \(\dfrac{3}{4}\%\)
      3. \(102\%\)
      1. Doce por ciento
      2. Un quinto por ciento
      1. 0.17
      2. 0.985
      3. \(0.00\bar{3}\)
      1. \(45\%\)
      2. \(475\%\)
      3. \(9.9\%\)
      1. \(\dfrac{1}{3}\)
      2. \(\dfrac{7}{50}\)
      3. \(2\dfrac{1}{2}\)
      1. \(20\%\)
      2. \(66.\bar{6}\% \text{ or } 66 \dfrac{2}{3}\%\)
      3. \(25\%\)
      1. 6.76
      2. 21.6
      3. 1,458
        1. $357.50
        2. 3,336.67
      2. $20,430.00
      3. $497.20
        1. $345.63
        2. $46.66
        3. $392.29
        4. 47,07$
        5. $439.36
      1. 40
      2. 76
      3. 180
      4. 160
      5. 900
      6. 300
        1. $279.30
        2. $312.82
      2. 6
      3. $2,090
      4. 3,401
      1. julio
      2. enero
      3. Incrementar
      4. Aproximadamente 9 grados
      5. La temperatura sube de enero a julio, y baja de julio a diciembre
      1. Aproximadamente 4,650 metros
      2. 3
      3. Montaña Combatiente y Monte Columbia
      4. Aproximadamente 950 metros
      1. 20
      2. Grados 2, 5, 7
      3. Kindergarten
      4. 15
      5. 110
      6. Aproximadamente\(19.5\%\)
      1. Vainilla
      2. Tarta y galleta
      3. 180
      4. \(20\%\)

     

    Descripciones de imagen

    Gráfica 1 (Gráfica de Líneas)

    Un gráfico de líneas muestra la temperatura promedio en Smithers, BC cada mes.

    • El eje horizontal enumera cada mes del año calendario.
    • El eje vertical es la temperatura en grados Celsius, y contiene los números -15 a 20 en incrementos de 5.

    Los datos del gráfico de líneas se representan en la siguiente tabla:

    Temperaturas promedio para Smithers, BC

    Mes (Eje Horizontal) Temperatura en Grados Celsius (Eje Vertical)
    enero \(~−9\)
    Febrero \(~−5\)
    marzo \(~0\)
    abril \(~5\)
    Mayo \(~9\)
    junio \(~12.5\)
    julio \(~15\)
    agosto \(~14\)
    septiembre \(~10\)
    Octubre \(~5\)
    noviembre \(~−2.5\)
    diciembre \(~−8\)

     

    Gráfica 2 (Gráfica de Barras)

    Un gráfico de barras muestra la altura de las montañas más altas de Columbia Británica en metros.

    • El eje horizontal enumera las siguientes montañas: Fairweather Mountain, Mount Quincy Adams, Mount Waddington, Mount Robson, Mount Root, Mount Tiedemann, Combatant Mountain, Mount Columbia y Asperity Mountain.
    • El eje vertical es la altura en metros, y contiene los números 5,000 en incrementos de 100.

    Los datos del gráfico de barras se representan en la siguiente tabla:

    Montañas más altas de Columbia Británica

    Montaña (Eje Horizontal) Altura en metros (Eje Vertical)
    Fairweather Montaña ~4,650
    Monte Quincy Adams ~4,100
    Monte Waddington ~4,000
    Monte Robson ~3,950
    Raíz de montaje ~3,900
    Monte Tiedemann ~3,850
    Montaña Combatiente ~3,750
    Mount Columbia ~3,750
    Montaña Asperity ~3,700
    Fuente: Statistics Canada, 2010

     

    Gráfica 3 (Gráfica de imagen)

    Un gráfico de imágenes muestra el número de alumnos de la Escuela Primaria Marmot que van en bicicleta a la escuela cada día por grado.

    • El eje vertical enumera los siguientes grados en la Escuela Primaria Marmot: Grado 7, Grado 6, Grado 5, Grado 3, Grado 2, Grado 1 y Kindergarten.
    • El eje horizontal contiene imágenes de bicicletas, con cada bicicleta representando a 5 ciclistas según la leyenda.
    • La población escolar total es de 563 alumnos.

    Los datos del gráfico de imagen se representan en la siguiente tabla:

    Número de alumnos que van en bicicleta a la escuela cada Día Escolar: Por grado en la Escuela Primaria Marmot

    Grado (Eje Vertical) Imágenes de Bikes (Horizontal Axis)
    Grado 7 4
    Grado 6 3
    Grado 5 4
    Grado 3 3
    Grado 2 4
    Grado 1 3
    Kindergarden 1

     

    Gráfica 4 (Gráfica Circular)

    Un gráfico circular muestra los sabores favoritos de helado por cada 1.000 personas.

    • La gráfica completa representa a las 1,000 personas encuestadas por su sabor favorito de helado.
    • Cada parte representa un sabor a helado y su popularidad como porcentaje del conjunto. Los sabores son (en sentido horario desde arriba): Vainilla, Fruta, Nuez, Caramelo, Chocolate y Pastel y Galleta.

    Los datos del gráfico circular se representan en la siguiente tabla:

    Sabores favoritos de helado: por 1000 personas

    Sabor Porcentaje del Total
    Vainilla 31%
    Fruto 18%
    Tuerca 16%
    Caramelo 14%
    Chocolate 11%
    Tarta y Galleta 10%

     

     

     

      Unidad 6: Revisión is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.