2.4: ¿Qué hay de malo con la pluralidad?
- Page ID
- 110508
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
La elección del Ejemplo 2 puede parecer totalmente limpia, pero hay un problema al acecho que surge cada vez que hay tres o más opciones. Mirando hacia atrás en nuestra mesa de preferencias, ¿cómo votarían nuestros miembros si solo tuvieran dos opciones?
Anaheim vs Orlando: 7 de los 10 preferirían Anaheim a Orlando
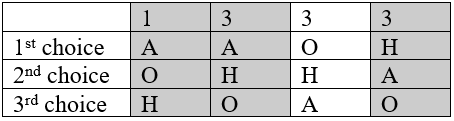
Anaheim vs Hawaii: 6 de cada 10 preferirían Hawái a Anaheim
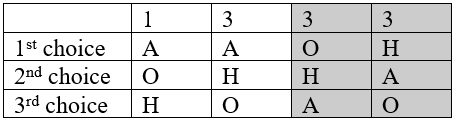
Esto no parece correcto, ¿verdad? Anaheim acaba de ganar las elecciones, sin embargo, 6 de cada 10 votantes, ¡el 60% de ellos, habrían preferido Hawai! Eso apenas parece justo. Marqués de Condorcet, filósofo, matemático y politólogo francés escribió sobre cómo esto podría suceder en 1785, y para él nombramos nuestro primer criterio de equidad.
Los criterios de equidad son declaraciones que parecen ser ciertas en una elección justa.
Si hay una opción que se prefiere en cada comparación uno a uno con las otras opciones, esa elección debería ser la ganadora. Llamamos a este ganador el Ganador de Condorcet, o Candidato de Condorcet.
En la elección del Ejemplo 2, ¿qué opción es el Ganador de Condorcet?
Solución
Vemos arriba que Hawaii es el preferido sobre Anaheim. Comparando Hawái con Orlando, podemos ver que 6 de cada 10 preferirían Hawái a Orlando.
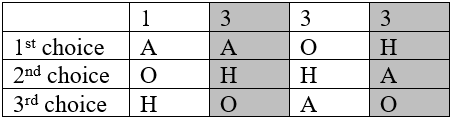
Dado que Hawái es el preferido en una comparación uno a uno con las otras dos opciones, Hawaii es el ganador del Condorcet.
Considera una elección de ayuntamiento en un distrito que históricamente es 60% votantes demócratas y 40% votantes republicanos. A pesar de que el ayuntamiento es técnicamente un cargo no partidista, la gente generalmente conoce las afiliaciones de los candidatos. En esta elección hay tres candidatos: Don y Key, ambos demócratas, y Elle, republicana. Un horario de preferencia para los votos se ve de la siguiente manera:
\ (\ begin {array} {|l|l|l|l|}
\ hline & 342 & 214 & 298\\
\ hline 1^ {\ text {st}}\ text {choice} &\ text {Elle} &\ text {Don} &\ text {Clave}\\
\ hline 2^ {\ texto {nd}}\ texto {elección} &\ texto {Don} &\ texto {Clave {} &\ text {Don }\\
\ hline 3^ {\ text {rd}}\ text {choice} &\ text {Key} &\ text {Elle} &\ text {Elle}\\
\ hline
\ end {array}\)
Solución
Podemos ver un total de\(342 + 214 + 298 = 854\) votantes que participaron en esta elección. Cálculo del porcentaje de votos del primer lugar:
Don:\(214/854 = 25.1\%\)
Clave:\(298/854 = 34.9\%\)
Elle:\(342/854 = 40.0\%\)
Por lo que en esta elección, los votantes demócratas dividieron su voto sobre los dos candidatos demócratas, permitiendo que la candidata republicana Elle ganara bajo el método de la pluralidad con el 40% de los votos.
Analizando más de cerca esta elección, vemos que viola el Criterio Condorcet. Analizando las comparaciones uno a uno:
Elle vs Don: 342 prefieren Elle; 512 prefieren Don: Don es preferido
Elle vs Clave: 342 prefieren Elle; 512 prefieren Clave: Clave es preferida
Don vs Clave: 556 prefieren Don; 298 prefieren Clave: Don es preferido
Entonces, a pesar de que Don tuvo el menor número de votos de primer lugar en la elección, es el ganador del Condorcet, siendo preferido en cada comparación uno a uno con los demás candidatos.
Considera la elección de Pruébalo Ahora 1. ¿Hay un ganador de Condorcet en esta elección?
- Contestar
-
Determinar el Ganador del Condorcet:
G vs M:\(44+14+20 = 78\) prefiera G,\(70+22+80=172\) prefiera M: M preferido
G vs B:\(44+14+20+70=148\) prefiera G,\(22+80+39 = 141\) prefiera B: G preferido
M vs B:\(44+70+22=136\) prefiera M,\(14+80+39=133\) prefiera B: M preferido
M es el ganador de Condorcet, en base a la información que tenemos.


