18.3.1: Introducción a logaritmos naturales y comunes
- Page ID
- 111448
- Usa una calculadora para encontrar logaritmos o potencias de base\(\ e\).
- Gráfica funciones exponenciales y logarítmicas de base\(\ e\).
- Encuentra logaritmos a bases distintas de\(\ e\) o 10 mediante el uso de la fórmula de cambio de base.
Introducción
Tanto en funciones exponenciales como en logaritmos, cualquier número puede ser la base. Sin embargo, hay dos bases que se utilizan con tanta frecuencia que los matemáticos tienen nombres especiales para sus logaritmos, ¡y las calculadoras científicas y gráficas incluyen claves específicamente para ellos! Estos son los logaritmos comunes y naturales.
Logaritmos comunes y\(\ e\)
Un logaritmo común es cualquier logaritmo con base 10. Recordemos que nuestro sistema numérico es base 10; hay diez dígitos del 0 al 9, y el valor posicional está determinado por grupos de diez. Se puede recordar un “logaritmo común”, entonces, como cualquier logaritmo cuya base sea nuestra base “común”, 10.
Los logaritmos naturales son diferentes a los logaritmos comunes. Si bien la base de un logaritmo común es 10, la base de un logaritmo natural es el número especial \(\ e\). Aunque esto parece una variable, representa un número irracional fijo aproximadamente igual a 2.718281828459. (Al igual que pi, continúa sin un patrón repetido en sus dígitos.) \(\ e\)a veces se le llama número de Euler o constante de Napier, y la carta\(\ e\) fue elegida para honrar al matemático Leonhard Euler (pronunciado encerado).
\(\ e\)es un número complicado pero interesante. Echemos un vistazo más de cerca a través de la lente de una fórmula que has visto antes: interés compuesto.
La fórmula para el interés compuesto es\(\ A=P\left(1+\frac{r}{m}\right)^{m t}\), donde\(\ A\) está la cantidad de dinero después de\(\ t\) años,\(\ P\) es la inversión principal o inicial,\(\ r\) es la tasa de interés anual (expresada como decimal, no como porcentaje),\(\ m\) es el número de períodos compuestos en un año, y \(\ t\)es el número de años.
Imagínese lo que sucede cuando la composición ocurre con frecuencia. Si el interés se compone anualmente, entonces\(\ m=1\). Si se compone mensualmente, entonces\(\ m=12\). La composición diaria estaría representada por\(\ m=365\); cada hora estaría representada por\(\ m=8,760\). Se puede ver que a medida que aumenta la frecuencia de los periodos compuestos, el valor de\(\ m\) aumenta rápidamente. ¡Imagínese el valor de\(\ m\) si los intereses se compusieran cada minuto o cada segundo!
Incluso puedes ir con más frecuencia que cada segundo, y eventualmente obtener compuestos continuamente. Mira los valores en esta tabla, que se parece mucho a la expresión multiplicada por\(\ P\) en la fórmula anterior. A medida\(\ x\) que aumenta, la expresión se asemeja más estrechamente a la composición continua.
| \(\ x\) | \(\ \left(1+\frac{1}{x}\right)^{x}\) |
| 1 | 2 |
| 10 | 2.59374... |
| 100 | 2.70481... |
| 1000 | 2.71692... |
| 10,000 | 2.71814... |
| 100,000 | 2.71826... |
| 1,000,000 | 2.71828... |
Observe que aunque\(\ x\) está aumentando mucho (¡multiplicando por 10 cada vez!) , el valor de no\(\ \left(1+\frac{1}{x}\right)^{x}\) está aumentando salvajemente. De hecho, se está acercando cada vez más a 2.718281828459... o al valor ahora llamado\(\ e\).
La función\(\ f(x)=e^{x}\) tiene muchas aplicaciones en economía, negocios y biología. e es un número importante por esta razón.
Trabajando con Bases de\(\ e\) y 10
Todas las calculadoras científicas y gráficas tienen claves que te ayudan a trabajar con e. Busca en tu calculadora y encuentra una etiquetada como “e” o “exp”. (Algunas calculadoras gráficas pueden requerir que uses un menú para encontrar e. Si no puedes ver la clave, consulta tu manual o pregunta a tu instructor.)
Cómo evaluar expresiones exponenciales usando\(\ e\) (como\(\ e^{3}\)) depende de tu calculadora. En algunas calculadoras, hay que presionar primero la\(\ \left[e^{x}\right]\) tecla luego ingresar al exponente y presionar enter. En otros ingresas primero al exponente y luego presionas la\(\ \left[e^{x}\right]\) tecla. Es importante que sepas cómo funciona tu calculadora. Con tu calculadora, intenta encontrar\(\ e^{3}\). El resultado debe ser 20.0855369... (el número de dígitos mostrados también dependerá de su calculadora).
Encuentra\(\ e^{1.5}\) usando una calculadora. Redondea tu respuesta a la centésima más cercana.
Solución
| Ingresa las pulsaciones de teclas necesarias para tu calculadora. Si tiene problemas para obtener la respuesta correcta, consulte su manual o instructor. | |
| 4.4816890... | Resultado de la calculadora. Después redondea la respuesta a la centésima más cercana. |
| 4.48 | Para ver esto resuelto en una calculadora, consulte los Ejemplos Trabajados para este tema. |
Se pueden encontrar potencias de 10 (la base común) de la misma manera. Algunas calculadoras tienen una\(\ \left[10^{\wedge}\right]\) o\(\ \left[10^{x}\right]\) clave que puedes usar para encontrar potencias de 10. Otra forma de encontrar potencias de 10 es usar la\(\ \left[x^{y}\right]\) o la\(\ \left[y^{x}\right]\) clave que funcionará con cualquier base (aunque si usas este método, tendrás que teclear dos números: la base, 10, y cualquier exponente al que la estés elevando).
Encuentra\(\ 10^{1.5}\), usando una calculadora. Redondea tu respuesta a la centésima más cercana.
Solución
| Ingresa las pulsaciones de teclas necesarias para tu calculadora. Si tiene problemas para obtener la respuesta correcta, consulte su manual o instructor. | |
| 31.6227766... | Resultado de la calculadora. Después redondea la respuesta a la centésima más cercana. |
| 31.62 | Para ver esto resuelto en una calculadora, consulte los Ejemplos Trabajados para este tema. |
Los logaritmos naturales (usando e como base) y logaritmos comunes (usando 10 como base) también están disponibles en calculadoras científicas y gráficas. Cuando se escribe un logaritmo sin una base entonces debes asumir que la base es 10. Por ejemplo:
\(\ \log 100=\log _{10} 100=2\)
Los logaritmos naturales también tienen su propio símbolo:\(\ \ln\).
\(\ \ln 100=\log _{e} 100=4.60517 \ldots\)
Las claves de logaritmo suelen ser más fáciles de encontrar, pero pueden funcionar de manera diferente de una calculadora a otra. La mayoría de las calculadoras científicas portátiles requieren que usted proporcione primero la entrada, luego presione la tecla\(\ [\log ]\) (común) o\(\ [\ln ]\) (natural). Otras calculadoras funcionan a la inversa: presione la\(\ [\ln ]\) tecla\(\ [\log]\) o, y luego proporcione la entrada y presione [Enter] o [=].
En su calculadora, encuentre la clave común de logaritmo (\(\ [\log ]\)o\(\ \left[\log _{10}\right]\)) y la clave de logaritmo natural (\(\ [\ln ]\)) y verifique que\(\ \ln 100=\log _{e} 100=4.60517 \ldots\)
Encuentra\(\ \ln 3\), usando una calculadora. Redondea tu respuesta a la centésima más cercana.
Solución
|
Recuerde\(\ \ln\) significa “logaritmo natural”, o\(\ \log _{e}\). Ingresa las pulsaciones de teclas necesarias para tu calculadora. Si tiene problemas para obtener la respuesta correcta, consulte su manual o instructor. |
|
| 1.098612... | Resultado de la calculadora. Después redondea la respuesta a la centésima más cercana. |
| 1.10 | Para ver esto resuelto en una calculadora, consulte los Ejemplos Trabajados para este tema. |
Encuentra\(\ \log 34\), usando una calculadora. Redondea tu respuesta a la centésima más cercana.
Solución
| Recuerde, cuando no se especifica ninguna base, este es el logaritmo común (base 10). Ingresa las pulsaciones de teclas necesarias para tu calculadora. Si tiene problemas para obtener la respuesta correcta, consulte su manual o instructor. | |
| 1.5314789... | Resultado de la calculadora. Después redondea la respuesta a la centésima más cercana. |
| 1.53 | Para ver esto resuelto en una calculadora, consulte los Ejemplos Trabajados para este tema. |
Usa una calculadora para encontrar\(\ \ln 7\).
- 0.845098...
- c
- 1096.633...
- 10,000,000
- Responder
-
- 0.845098...
Incorrecto. Encontraste el valor de\(\ \log 7\), es decir,\(\ \log _{10} 7\). La respuesta correcta es 1.945910...
- 0.845098...
Correcto. Identificaste correctamente las claves en tu calculadora y encontraste el natural\(\ \log\) de 7.
- 1096.633...
Incorrecto. Encontraste el valor de\(\ e^{7}\). La respuesta correcta es 1.945910...
- 10,000,000
Incorrecto. Encontraste el valor de\(\ 10^{7}\). La respuesta correcta es 1.945910...
- 0.845098...
Graficando Funciones Exponenciales y Logarítmicas de Base\(\ e\)
Graficar funciones con la base no\(\ e\) es diferente a graficar otras funciones exponenciales y logarítmicas: crear una tabla de valores, trazar los puntos y conectarlos con una curva suave. Usted querrá usar una calculadora al crear la tabla.
Gráfica\(\ f(x)=e^{x}\).
Solución
| \ (\\ begin {array} {c|c} x & f (x)\\ \ hline-2 & 0.1353\ ldots\\ -1 & 0.3678\ ldots\\ 0 & 1\\ 1 & 2.7182\ ldots\\ 2 & 7.3890\ ldots \ end {array}\) |
Comience con una tabla de valores. No olvides elegir valores positivos y negativos para\(\ x\). Usa una calculadora para encontrar los\(\ f(x)\) valores. |
| \ (\\ begin {array} {|c} (x, y)\ text {pares}\\ \ hline (-2,0.1353\ ldots)\\ (-1,0.3678\ ldots)\\ (0.1)\ (1,2.7182\ lpuntos)\\ (2,7.3890\ ldots) \ end {array}\) |
Si piensas en\(\ f(x)\), como\(\ y\), cada fila forma un par ordenado que puedes trazar en una cuadrícula de coordenadas. |
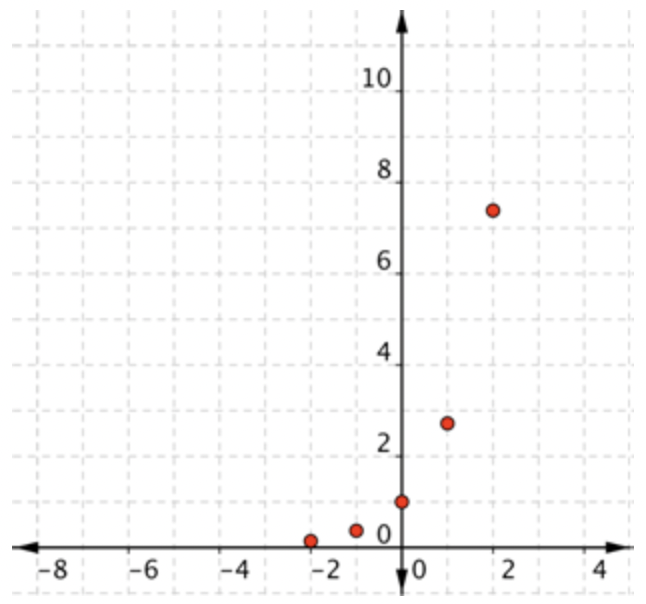 |
Trazar los puntos. |
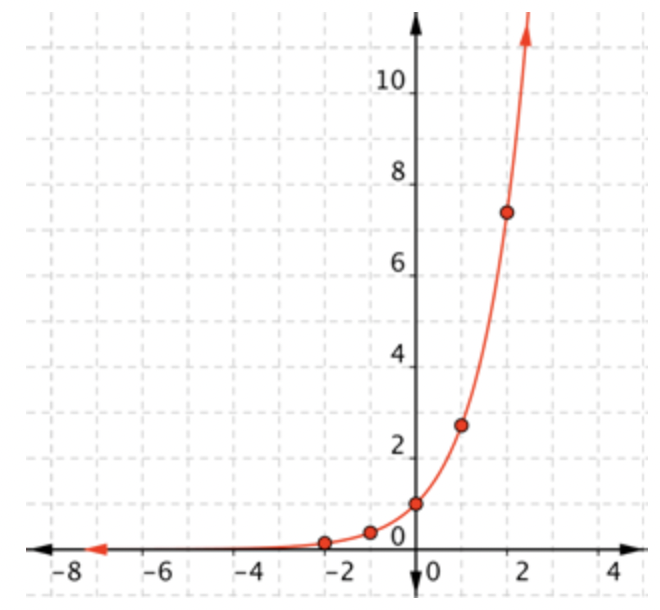 |
Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas). Usa la forma de una gráfica exponencial para ayudarte: la gráfica se acerca al eje x a la izquierda, y se vuelve cada vez más pronunciada a la derecha. |
El mismo proceso funciona para funciones logarítmicas. Elige\(\ x\) valores y usa una calculadora para encontrar los\(\ y\) valores.
Gráfica\(\ f(x)=\ln x\).
Solución
| \ (\\ begin {array} {c|c} x & f (x)\\ \ hline 0.1 & -2.30\ ldots\\ 0.5 & -0.69\ ldots\\ 1 & 0\\ e & 1\\ 5 & 1.60\ ldots\\ 10 y 2.30\ ldots \ end {array}\) |
Comience con una tabla de valores. Si eliges\(\ x\) valores, recuerda que\(\ x\) deben ser mayores a 0. Elija valores mayores y menores que la base (la base y 1 también son buenas opciones para\(\ x\) los valores). |
| \ (\\ begin {array} {c} (x, y)\ text {pares}\\ \ hline (0.1, -2.30\ ldots)\\ (0.5, -0.69\ ldots)\\ (1,0)\ (e, 1)\\ (5,1.60\ ldots)\\ (10,2.30\ ldots) \ end {array}\) |
Si piensas en eso\(\ y\), cada fila forma un par ordenado que puedes trazar en una cuadrícula de coordenadas.\(\ f(x)\) |
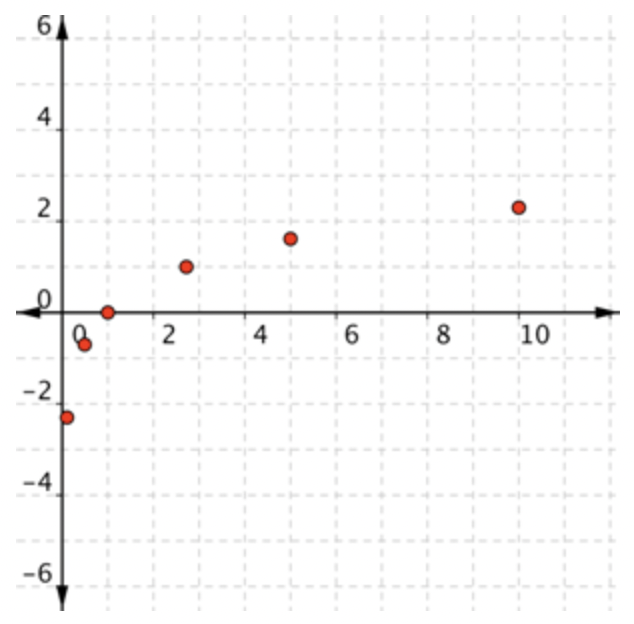 |
Trazar los puntos. |
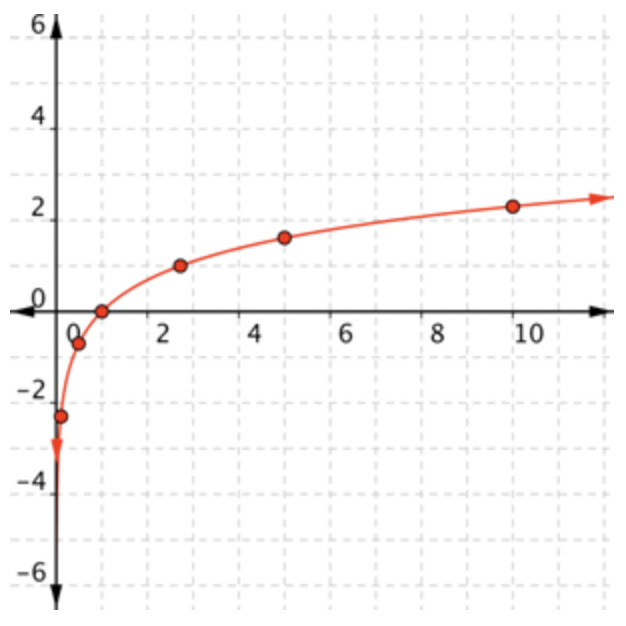 |
Conecta los puntos lo mejor que puedas, usando una curva suave (no una serie de líneas rectas). Usa la forma de una gráfica logarítmica para ayudarte: la gráfica se acerca al eje y por\(\ x\) cerca de 0. |
En ocasiones las entradas al logaritmo, o el exponente sobre la base, serán más complicadas que una sola variable. En esos casos, asegúrese de usar la entrada correcta en la calculadora.
Nota: Si su calculadora usa el método “input last” para logaritmos, calcule la entrada por separado y anótelo, o use paréntesis para asegurarse de que se usa la entrada correcta. Por ejemplo, al calcular\(\ \log (3 x)\) cuándo\(\ x=4\), la respuesta correcta es 1.079.... Si no usas los paréntesis, la calculadora encontrará\(\ \log 3\), y multiplicará eso por 4 para obtener 1.908...
Gráfica\(\ f(x)=\ln 4 x\).
Solución
| \ (\\ begin {array} {c|c|c} x & 4 x & f (x)\ \ hline 0.1 & 0.4 & -0.91\ ldots\\ 0.5 & 2 & 0.69\ ldots\\ 1 & 4 & 1.38\ ldots\\ 3 & 12 y 2.48 \ ldots\\ 10 & 40 & 3.68\ ldots \ end {array}\) |
Crear una tabla de valores. Aunque todo se podría hacer usando la calculadora, incluyamos una columna para la entrada del logaritmo. Esto te ayuda a evitar errores en la calculadora. |
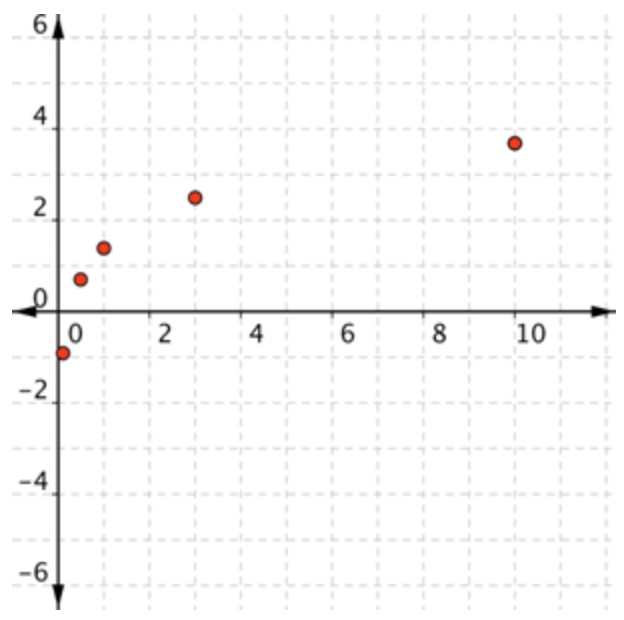 |
Utilice los pares de tablas para trazar puntos. Es posible que desee elegir valores adicionales para la tabla para dar una mejor idea para toda la gráfica visible. |
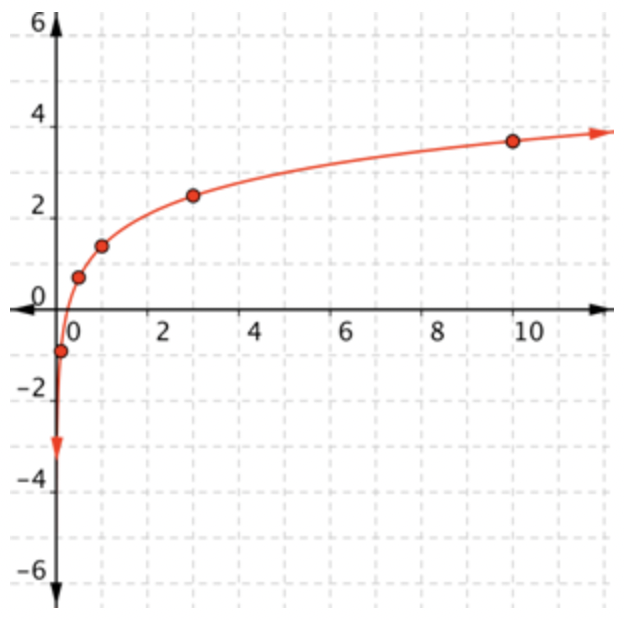 |
Conecta los puntos lo mejor que puedas, usando una curva suave. |
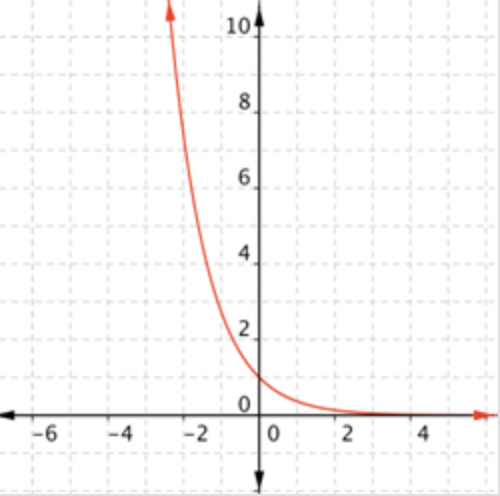
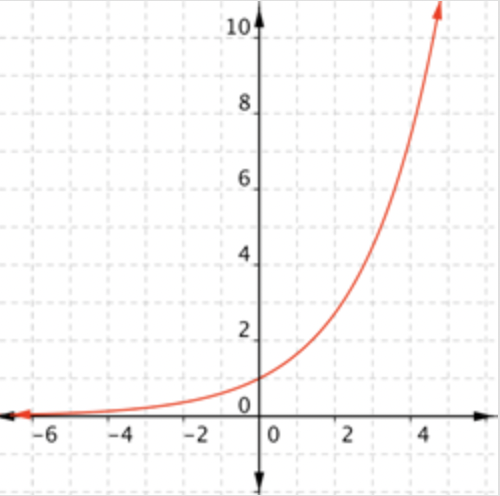
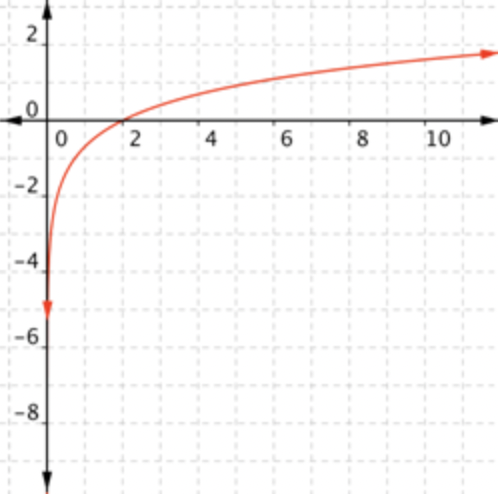
¿Cuál de las siguientes es una gráfica\(\ f(x)=e^{0.5 x}\)?
- Responder
-
Encontrar logaritmos de otras bases
Ahora ya sabes cómo encontrar\(\ e\) logaritmos base 10 y base de cualquier número. ¿Y si quisieras calcular\(\ \log _{7} 36\)? Convirtiendo a una ecuación exponencial, tienes\(\ 7^{x}=36\). Sabes que\(\ 7^{1}\) es 7, y\(\ 7^{2}\) es 49, así que puedes razonar que\(\ x\) debe estar entre 1 y 2, probablemente muy cerca de 2. Pero, ¿qué tan cerca? No tienes una clave para la base 7, por lo que usas una fórmula Change of Base para cambiar la base de una función de registro a otra base.
\(\ \log _{b} x=\frac{\log _{a} x}{\log _{a} b}\)
Observe que\(\ a\) aparece como base en ambos logaritmos del lado derecho de la fórmula. Por ejemplo,\(\ \log _{7} 36=\frac{\log 36}{\log 7}\), usando una nueva base de 10. También se podría decir\(\ \log _{7} 36=\frac{\ln 36}{\ln 7}\), o incluso\(\ \log _{7} 36=\frac{\log _{362} 36}{\log _{362} 7}\). Por supuesto, esa última no es más fácil de calcular que la expresión original, pero usando las\(\ [\ln ]\) claves\(\ [\log]\) o en una calculadora, puedes\(\ \frac{\ln 36}{\ln 7}\) usar\(\ \frac{\log 36}{\log 7}\) o encontrar\(\ \log _{7} 36\).
Encontrar\(\ \log _{7} 36\).
Solución
| \(\ \log _{7} 36=\frac{\log 36}{\log 7}\) | Usa la fórmula Cambio de Base. Se pueden utilizar logaritmos comunes o logaritmos naturales. Para este ejemplo, usemos logaritmos comunes. |
| \(\ \frac{\log 36}{\log 7}=\frac{1.55630 \ldots}{0.84509 \ldots}=1.84156 \ldots\) | Utilice la calculadora para evaluar el cociente. |
\(\ 1.84156 \ldots\)
Si hubieras usado logaritmos naturales, habrías obtenido la misma respuesta:\(\ \log _{7} 36=\frac{\ln 36}{\ln 7}=\frac{3.5835 \ldots}{1.9459 \ldots}=1.84156 \ldots\)
Encontrar\(\ \log _{3} 25.9\).
Solución
| \(\ \log _{3} 25.9=\frac{\ln 25.9}{\ln 3}\) | Usa la fórmula Cambio de Base. Esta vez, usemos logaritmos naturales. |
| \(\ \frac{\ln 25.9}{\ln 3}=\frac{3.2542 \ldots}{1.0986 \ldots}=2.9621 \ldots\) | Evaluar el cociente. |
2.9621
Encontrar\(\ \log _{5} 200\).
- 40
- 0.303...
- 3.292...
- 2.301...
- Responder
-
- 40
Incorrecto. Encontraste el valor de\(\ 200 \div 5\). La respuesta correcta es 3.292...
- 0.303...
Incorrecto. Al usar la fórmula Cambio de base, el log de la base original es el denominador:\(\ \log _{5} 200=\frac{\log 200}{\log 5}=\frac{\ln 200}{\ln 5}\). La respuesta correcta es 3.292...
- 3.292...
Correcto. \(\ \log _{5} 200=\frac{\log 200}{\log 5}=\frac{\ln 200}{\ln 5}=3.292 \ldots\)
- 2.301...
Incorrecto. Encontraste el valor de\(\ \log 200\). La respuesta correcta es 3.292...
- 40
Resumen
A menudo se utilizan logaritmos comunes (base 10, escritos\(\ \log x\) sin base) y logaritmos naturales (base\(\ e\), escritos\(\ \ln x\)). Las calculadoras científicas y gráficas tienen claves o elementos de menú que le permiten encontrar fácilmente\(\ \log x\) y\(\ \ln x\), así como\(\ 10^{x}\) y\(\ e^{x}\). Usando estas claves y el cambio de fórmula base, puedes encontrar logaritmos en cualquier base.