11.3: Aplicación de Distribuciones Normales
- Page ID
- 113048
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Aplicar las características de una distribución normal a la resolución de aplicaciones.
Introducción
La distribución normal es la base de la inferencia estadística y será parte esencial de muchos de esos temas en capítulos posteriores. Mientras tanto, esta sección cubrirá algunos de los tipos de preguntas que se pueden responder utilizando las propiedades de una distribución normal. Los primeros ejemplos tratan de cuestiones más teóricas que te ayudarán a dominar entendimientos básicos y habilidades computacionales, mientras que los problemas posteriores proporcionarán ejemplos con datos reales, o al menos un contexto real.
Distribuciones normales con datos reales
La base de realizar experimentos mediante la recolección de encuestas y muestras se basa más a menudo en la distribución normal, ya que aprenderá con mayor detalle en capítulos posteriores. Aquí hay dos ejemplos para comenzar.
El Centro de Información del Servicio Nacional de Salud en Gran Bretaña recopila y publica una gran cantidad de información y estadísticas sobre temas de salud que afectan a la población. Uno de esos conjuntos de datos completos rastrea la información sobre la salud de los niños [1]. Según sus estadísticas, en 2006, la estatura media de los niños de 12 años fue de 152.9 cm, con una desviación estándar estimada de aproximadamente 8.5 cm. (Estas no son las cifras exactas para la población, y en capítulos posteriores, aprenderemos cómo se calculan y qué tan precisas pueden ser, pero por ahora, asumiremos que son una estimación razonable de los parámetros verdaderos). Si Cecil, de 12 años, mide 158 cm, aproximadamente, ¿qué porcentaje de todos los niños de 12 años en Gran Bretaña es más alto que?
Solución
Primero debemos asumir que la altura de los niños de 12 años en Gran Bretaña normalmente se distribuye, y esto parece una suposición razonable de hacer. Como siempre, dibujar un boceto y estimar una respuesta razonable antes de calcular el porcentaje. En este caso, usemos la calculadora para bosquejar la distribución y el sombreado. Primero, decida sobre una ventana apropiada que incluya aproximadamente 3 desviaciones estándar a cada lado de la media. En este caso, 3 desviaciones estándar es de aproximadamente 25.5 cm, por lo que sumar y restar este valor a/de la media para encontrar los extremos horizontales. Luego ingrese el comando apropiado 'ShadoNORM ('como se muestra:

A partir de estos datos, estimamos que Cecil es más alto que alrededor del 73% de los niños de 12 años. También podríamos formular nuestra suposición de esta manera: la probabilidad de que un niño británico de 12 años seleccionado al azar sea más bajo que Cecil es de aproximadamente 0.73. A menudo con datos como este, usamos percentiles. Diríamos que Cecil está en el percentil 73 rd para la estatura entre los niños de 12 años de Gran Bretaña.
¿Qué tan alto tendría que ser Cecil para estar entre el 1% superior de todos los niños de 12 años en Gran Bretaña?
Aquí hay un boceto:

En este caso, se nos da el porcentaje, por lo que necesitamos usar el comando 'InvNorm ('como se muestra.

Nuestros resultados indican que Cecil necesitaría tener alrededor de 173 cm de altura para estar en el 1% superior de los niños de 12 años en Gran Bretaña.
Supongamos que la distribución de las masas de iguanas marinas hembras en Puerto Villamil en las Islas Galápagos es aproximadamente normal, con una masa media de 950 g y una desviación estándar de 325 g. Hay muy pocas iguanas marinas jóvenes en las zonas pobladas de las islas, porque los gatos salvajes tienden a matarlas . ¿Qué tan raro es que encontremos en esta zona una iguana marina hembra con una masa inferior a 400 g?
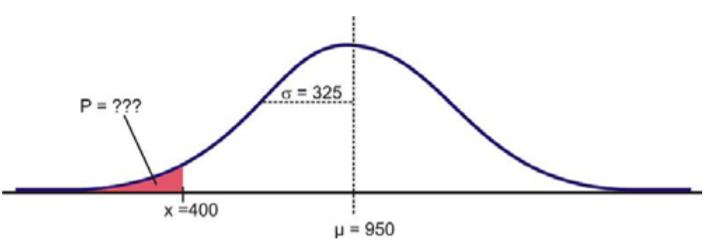
Solución
Usando una calculadora gráfica, podemos aproximar la probabilidad de que una iguana marina hembra sea menor a 400 gramos de la siguiente manera:
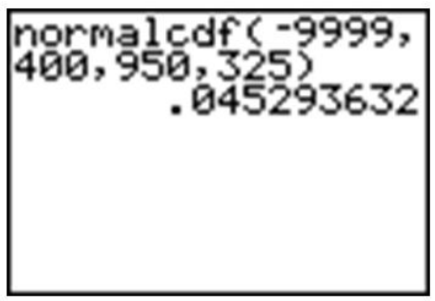
Con una probabilidad de aproximadamente 0.045, o sólo alrededor del 5%, podríamos decir que es bastante improbable que encontremos una iguana tan pequeña.
La planta física en el campus principal de una gran universidad estatal recibe diariamente solicitudes para reemplazar bombillas fluorescentes. La distribución del número de solicitudes diarias tiene forma de campana y tiene una media de 59 y una desviación estándar de 9. Usando la regla empírica, ¿cuál es el porcentaje aproximado de solicitudes de reemplazo de bombillas que suman entre 59 y 77?
Solución
Ya que queremos utilizar la Regla Empírica, debemos dibujar una figura que refleje la Regla Empírica dada la media es\(59\) y la desviación estándar es\(9\). Recordemos, 1 desviación estándar de la media es\(59 ± 9\), dos desviaciones estándar de la media es\(59 ± 2 \cdot 9\), y 3 desviaciones estándar de la media es\(59 ± 3 \cdot 9\).

Una vez que hagamos esta cifra, podemos fácilmente el porcentaje de solicitudes de reemplazo de bombilla numerando entre 59 y 77:
\(34 \% + 13.5 \% = 47.5 \%\)
Así,\(47.5 \%\) de las solicitudes de sustitución de bombillas numeradas entre 59 y 77.
Una empresa tiene una política de retirar los autos de la compañía; esta política analiza el número de millas recorridas, el propósito de los viajes, el estilo de automóvil y otras características. La distribución del número de meses en servicio para la flota de automóviles tiene forma de campana y tiene una media de 41 meses y una desviación estándar de 5 meses. Utilizando la Regla Empírica, ¿cuál es el porcentaje aproximado de autos que permanecen en servicio entre 46 y 56 meses?
Solución
Como queremos usar la Regla Empírica, debemos dibujar una figura que refleje la Regla Empírica dado que la media es 41 y la desviación estándar es 5:

Una vez que hagamos esta cifra, podemos fácilmente el porcentaje aproximado de autos que permanecen en servicio entre 46 y 56 meses:
\(13.5 \% + 2.35 \% = 15.85 \%\)
Así,\(15.85 \%\) de los autos permanecen en servicio entre 46 y 56 meses.
Ejercicios
1. ¿Cuál de los siguientes intervalos contiene el 95% medio de los datos en una distribución normal estándar?
a)\(z < 2\)
b)\(z ≤ 1.645\)
c)\(z ≤ 1.96\)
d)\(−1.645 ≤ z ≤ 1.645\)
e)\(−1.96 ≤ z ≤ 1.96\)
2. El proceso de fabricación en una fábrica de piezas metálicas produce una ligera variación en el diámetro de los rodamientos de bolas de metal. Los expertos en control de calidad afirman que los rodamientos producidos tienen un diámetro medio de 1.4 cm. Si el diámetro es más de 0.0035 cm demasiado ancho o demasiado estrecho, no funcionarán correctamente. Para mantener su reputación confiable, la compañía desea garantizar que no más de una décima parte del 1% de los rodamientos que se fabrican sean ineficaces. ¿Cuál sería la desviación estándar de los rodamientos fabricados para cumplir con este objetivo?
3. Supongamos que el envoltorio de cierta barra de caramelo enumera su peso como 2.13 onzas. Naturalmente, los pesos de las barras individuales varían algo. Supongamos que los pesos de estas barras de caramelo varían según una distribución normal, con\(µ = 2.2\)\(σ = 0.04\) onzas y onzas.
a) ¿Qué proporción de las barras de caramelo pesan menos que el peso anunciado?
b) ¿Qué proporción de las barras de caramelo pesan entre 2.2 y 2.3 onzas?
c) ¿Una barra de chocolate de qué peso sería más pesada que todas menos el 1% de las barras de caramelo que hay afuera?
d) Si el fabricante quiere ajustar el proceso de producción para que no más de 1 barra de caramelo en 1000 pese menos que el peso anunciado, ¿cuál sería la media de los pesos reales que tendría que ser? (Supongamos que la desviación estándar sigue siendo la misma.)
e) Si el fabricante quiere ajustar el proceso de producción para que la media se mantenga en 2.2 onzas y no más de 1 barra de caramelo en 1000 pese menos que el peso anunciado, ¿qué tan pequeña debe ser la desviación estándar de los pesos?
4. The Acme Company fabrica widgets. La distribución de los pesos de los widgets es en forma de campana. Los pesos de los widgets tienen una media de 51 onzas y una desviación estándar de 4 onzas. Utilice la Regla Empírica para responder a las siguientes preguntas.
a) El 99.7% de los pesos de los widgets se encuentran entre qué dos pesos?
b) ¿Qué porcentaje de los pesos de los widgets se encuentran entre 43 y 63 onzas?
c) ¿Qué porcentaje de los pesos de los widgets se encuentran por encima de 47?
|
Área Normal Estándar de Mesa bajo la Curva Normal de 0 a z
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.00 | 0.00000 | 0.00399 | 0.00798 | 0.01197 | 0.01595 | 0.01994 | 0.02392 | 0.02790 | 0.03188 | 0.03586 |
| 0.10 | 0.03983 | 0.04380 | 0.04776 | 0.05172 | 0.05567 | 0.05962 | 0.06356 | 0.06749 | 0.07142 | 0.07535 |
| 0.20 | 0.07926 | 0.08317 | 0.08706 | 0.09095 | 0.09483 | 0.09871 | 0.10257 | 0.10642 | 0.11026 | 0.11409 |
| 0.30 | 0.11791 | 0.12172 | 0.12552 | 0.12930 | 0.13307 | 0.13683 | 0.14058 | 0.14431 | 0.14803 | 0.15173 |
| 0.40 | 0.15542 | 0.15910 | 0.16276 | 0.16640 | 0.17003 | 0.17364 | 0.17724 | 0.18082 | 0.18439 | 0.18793 |
| 0.50 | 0.19146 | 0.19497 | 0.19847 | 0.20194 | 0.20540 | 0.20884 | 0.21226 | 0.21566 | 0.21904 | 0.22240 |
| 0.60 | 0.22575 | 0.22907 | 0.23237 | 0.23565 | 0.23891 | 0.24215 | 0.24537 | 0.24857 | 0.25175 | 0.25490 |
| 0.70 | 0.25804 | 0.26115 | 0.26424 | 0.26730 | 0.27035 | 0.27337 | 0.27637 | 0.27935 | 0.28230 | 0.28524 |
| 0.80 | 0.28814 | 0.29103 | 0.29389 | 0.29673 | 0.29955 | 0.30234 | 0.30511 | 0.30785 | 0.31057 | 0.31327 |
| 0.90 | 0.31594 | 0.31859 | 0.32121 | 0.32381 | 0.32639 | 0.32894 | 0.33147 | 0.33398 | 0.33646 | 0.33891 |
| 1.00 | 0.34134 | 0.34375 | 0.34614 | 0.34849 | 0.35083 | 0.35314 | 0.35543 | 0.35769 | 0.35993 | 0.36214 |
| 1.10 | 0.36433 | 0.36650 | 0.36864 | 0.37076 | 0.37286 | 0.37493 | 0.37698 | 0.37900 | 0.38100 | 0.38298 |
| 1.20 | 0.38493 | 0.38686 | 0.38877 | 0.39065 | 0.39251 | 0.39435 | 0.39617 | 0.39796 | 0.39973 | 0.40147 |
| 1.30 | 0.40320 | 0.40490 | 0.40658 | 0.40824 | 0.40988 | 0.41149 | 0.41308 | 0.41466 | 0.41621 | 0.41774 |
| 1.40 | 0.41924 | 0.42073 | 0.42220 | 0.42364 | 0.42507 | 0.42647 | 0.42785 | 0.42922 | 0.43056 | 0.43189 |
| 1.50 | 0.43319 | 0.43448 | 0.43574 | 0.43699 | 0.43822 | 0.43943 | 0.44062 | 0.44179 | 0.44295 | 0.44408 |
| 1.60 | 0.44520 | 0.44630 | 0.44738 | 0.44845 | 0.44950 | 0.45053 | 0.45154 | 0.45254 | 0.45352 | 0.45449 |
| 1.70 | 0.45543 | 0.45637 | 0.45728 | 0.45818 | 0.45907 | 0.45994 | 0.46080 | 0.46164 | 0.46246 | 0.46327 |
| 1.80 | 0.46407 | 0.46485 | 0.46562 | 0.46638 | 0.46712 | 0.46784 | 0.46856 | 0.46926 | 0.46995 | 0.47062 |
| 1.90 | 0.47128 | 0.47193 | 0.47257 | 0.47320 | 0.47381 | 0.47441 | 0.47500 | 0.47558 | 0.47615 | 0.47670 |
| 2.00 | 0.47725 | 0.47778 | 0.47831 | 0.47882 | 0.47932 | 0.47982 | 0.48030 | 0.48077 | 0.48124 | 0.48169 |
| 2.10 | 0.48214 | 0.48257 | 0.48300 | 0.48341 | 0.48382 | 0.48422 | 0.48461 | 0.48500 | 0.48537 | 0.48574 |
| 2.20 | 0.48610 | 0.48645 | 0.48679 | 0.48713 | 0.48745 | 0.48778 | 0.48809 | 0.48840 | 0.48870 | 0.48899 |
| 2.30 | 0.48928 | 0.48956 | 0.48983 | 0.49010 | 0.49036 | 0.49061 | 0.49086 | 0.49111 | 0.49134 | 0.49158 |
| 2.40 | 0.49180 | 0.49202 | 0.49224 | 0.49245 | 0.49266 | 0.49286 | 0.49305 | 0.49324 | 0.49343 | 0.49361 |
| 2.50 | 0.49379 | 0.49396 | 0.49413 | 0.49430 | 0.49446 | 0.49461 | 0.49477 | 0.49492 | 0.49506 | 0.49520 |
| 2.60 | 0.49534 | 0.49547 | 0.49560 | 0.49573 | 0.49585 | 0.49598 | 0.49609 | 0.49621 | 0.49632 | 0.49643 |
| 2.70 | 0.49653 | 0.49664 | 0.49674 | 0.49683 | 0.49693 | 0.49702 | 0.49711 | 0.49720 | 0.49728 | 0.49736 |
| 2.80 | 0.49744 | 0.49752 | 0.49760 | 0.49767 | 0.49774 | 0.49781 | 0.49788 | 0.49795 | 0.49801 | 0.49807 |
| 2.90 | 0.49813 | 0.49819 | 0.49825 | 0.49831 | 0.49836 | 0.49841 | 0.49846 | 0.49851 | 0.49856 | 0.49861 |
| 3.00 | 0.49865 | 0.49869 | 0.49874 | 0.49878 | 0.49882 | 0.49886 | 0.49889 | 0.49893 | 0.49896 | 0.49900 |
| 3.10 | 0.49903 | 0.49906 | 0.49910 | 0.49913 | 0.49916 | 0.49918 | 0.49921 | 0.49924 | 0.49926 | 0.49929 |
| 3.20 | 0.49931 | 0.49934 | 0.49936 | 0.49938 | 0.49940 | 0.49942 | 0.49944 | 0.49946 | 0.49948 | 0.49950 |
| 3.30 | 0.49952 | 0.49953 | 0.49955 | 0.49957 | 0.49958 | 0.49960 | 0.49961 | 0.49962 | 0.49964 | 0.49965 |
| 3.40 | 0.49966 | 0.49968 | 0.49969 | 0.49970 | 0.49971 | 0.49972 | 0.49973 | 0.49974 | 0.49975 | 0.49976 |
| 3.50 | 0.49977 | 0.49978 | 0.49978 | 0.49979 | 0.49980 | 0.49981 | 0.49981 | 0.49982 | 0.49983 | 0.49983 |
| 3.60 | 0.49984 | 0.49985 | 0.49985 | 0.49986 | 0.49986 | 0.49987 | 0.49987 | 0.49988 | 0.49988 | 0.49989 |
| 3.70 | 0.49989 | 0.49990 | 0.49990 | 0.49990 | 0.49991 | 0.49991 | 0.49992 | 0.49992 | 0.49992 | 0.49992 |
| 3.80 | 0.49993 | 0.49993 | 0.49993 | 0.49994 | 0.49994 | 0.49994 | 0.49994 | 0.49995 | 0.49995 | 0.49995 |
| 3.90 | 0.49995 | 0.49995 | 0.49996 | 0.49996 | 0.49996 | 0.49996 | 0.49996 | 0.49996 | 0.49997 | 0.49997 |
| 4.00 | 0.49997 | 0.49997 | 0.49997 | 0.49997 | 0.49997 | 0.49997 | 0.49998 | 0.49998 | 0.49998 | 0.49998 |



