4.8: Orden de Operaciones con Fracciones

Empecemos por tomar poderes de fracciones. Recordemos que

\[ a^m = \underbrace{a \cdot a \cdot ... \cdot a}_{m \text{ times}}\nonumber \]

Ejemplo 1

Simplificar: (−3/4) ².

Solución

Por definición,

\[ \begin{aligned} \left( - \frac{3}{4} \right)^2 = \left( - \frac{3}{4} \right) \left( - \frac{3}{4} \right) ~& \textcolor{red}{ \text{ Fact: } a^2 = a \cdot a.} \\ = \frac{3 \cdot 3}{4 \cdot 4} ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply numerators and denominators.} \\ \text{ Product of even number of negative factors is positive.} \end{array}} \\ = \frac{9}{16} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Ejercicio

Simplificar:

\[ \left( - \frac{2}{5} \right)^2\nonumber \]

Contestar

4/25

Ejemplo 2

Simplificar: (−2/3) ³.

Solución

Por definición,

\[ \begin{aligned} \left( - \frac{2}{3}\right)^3 = \left( - \frac{2}{3} \right) \left( - \frac{2}{3} \right) \left( - \frac{2}{3} \right) ~ & \textcolor{red}{ \text{ Fact: } a^3 = a \cdot a \cdot a.} \\ = - \frac{2 \cdot 2 \cdot 2}{3 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \begin{array} ~ \text{ Multiply numerators and denominators.} \\ \text{ Product of odd number of negative factors is negative.} \end{array}} \\ = - \frac{8}{27} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Ejercicio

Simplificar:

\[ \left( - \frac{1}{6} \right)^3\nonumber \]

Contestar

−1/216

Los dos últimos ejemplos reiteran un principio aprendido anteriormente.

Par e impar

• El producto de un número par de factores negativos es positivo.
• El producto de un número impar de factores negativos es negativo.

Orden de Operaciones

Para mayor comodidad, repetimos aquí las reglas que guían el orden de las operaciones.

Reglas que guían el orden de operaciones

Al evaluar expresiones, proceda en el siguiente orden.

1. Evalúe primero las expresiones contenidas en los símbolos de agrupación. Si los símbolos de agrupación están anidados, evalúe primero la expresión en el par más interno de símbolos de agrupación.
2. Evaluar todos los exponentes que aparecen en la expresión.
3. Realizar todas las multiplicaciones y divisiones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.
4. Realizar todas las sumas y restaciones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.

Ejemplo 3

Simplificar:\(- \frac{1}{2} + \frac{1}{4} \left( - \frac{1}{3} \right)\).

Solución

Multiplique primero, luego agregue.

\[ \begin{aligned} - \frac{1}{2} + \frac{1}{4} \left( - \frac{1}{3} \right) = - \frac{1}{2} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Multiply: } \frac{1}{4} \left( - \frac{1}{3} \right) = - \frac{1}{12}.} \\ = - \frac{1 \cdot \textcolor{red}{6}}{2 \cdot \textcolor{red}{6}} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 12.}} \\ = - \frac{6}{12} + \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = - \frac{7}{12} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]

Ejercicio

Simplificar:\( - \frac{2}{3} + \frac{3}{4} \left( - \frac{1}{2} \right)\)

Contestar

−25/24

Ejemplo 4

Simplificar:\(2 \left( - \frac{1}{2} \right)^2 +4 \left( - \frac{1}{2} \right)\).

Solución

Los exponentes primero, luego se multiplican, luego se suman.

\[ \begin{aligned} 2 \left( - \frac{1}{2} \right)^2 + 4 \left( - \frac{1}{2} \right) = 2 \left( \frac{1}{4} \right) + 4 \left( - \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ Exponent first: } \left( - \frac{1}{2} \right)^2 = \frac{1}{4}.} \\ = \frac{1}{2} + \left( - \frac{2}{1} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply: } 2 \left( \frac{1}{4} \right) = \frac{1}{2} \\ \text{ and } 4 \left( - \frac{1}{2} \right) = - \frac{2}{1}. \end{array}} \\ = \frac{1}{2} + \left( - \frac{2 \cdot \textcolor{red}{2}}{1 \cdot \textcolor{red}{2}} \right) ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 2.}} \\ = \frac{1}{2} + \left( - \frac{4}{2} \right) ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = - \frac{3}{2} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]

Ejercicio

Simplificar:\(3 \left( - \frac{1}{3} \right)^2 - 2 \left( - \frac{1}{3} \right)\)

Contestar

1

Ejemplo 5

Dado a = −3/4, b = 1/2, c = 1/3 y d = −1/4, evalúe la expresión ab − cd.

Solución

Recordemos que es una buena práctica preparar paréntesis antes de sustituir.

\[ ad - bc = ( ~ ) (~) - (~)(~)\nonumber \]

Sustituya los valores dados en la expresión algebraica, luego simplifique usando el orden de las operaciones.

\[ \begin{aligned} ab - cd = \left( - \frac{3}{4} \right) \left( \frac{1}{2} \right) - \left( \frac{1}{3} \right) \left( - \frac{1}{4} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Substitute: } -3/4 \text{ for } a, ~ 1/2 \text{ for } b, \\ 1/3 \text{ for } c, ~ \text{ and } -1/4 \text{ for } d. \end{array}} \\ = - \frac{3}{8} - \left( - \frac{1}{12} \right) ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply first: } \left( - \frac{3}{4} \right) \left( \frac{1}{2} \right) = - \frac{3}{8} \\ \text{ and } \left( \frac{1}{3} \right) \left( - \frac{1}{4} \right) = - \frac{1}{12}. \end{array}} \\ = - \frac{3}{8} + \frac{1}{12} ~ & \textcolor{red}{ \text{ Subtract by adding opposite.}} \\ = - \frac{3 \cdot \textcolor{red}{3}}{8 \cdot \textcolor{red}{3}} + \frac{1 \cdot \textcolor{red}{2}}{12 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions; LCD = 24.}} \\ = - \frac{9}{24} + \frac{2}{24} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = - \frac{7}{24} ~ & \textcolor{red}{ \text{ Add over common denominator.}} \end{aligned}\nonumber \]

Ejercicio

Dado a = −1/2, b = 1/3, y c = −1/5, evaluar a + bc.

Contestar

−17/30

Ejemplo 6

Dado a = −1/4 y b = 1/2, evaluar (a ² − b ²) ÷ (a + b).

Solución

Recordemos que es una buena práctica preparar paréntesis antes de sustituir.

\[ (a^2 - b^2 ) \div (a+b) - \left( (~)^2 - (~)^2 \right) \div \left( (~) + (~) \right)\nonumber \]

Sustituya los valores dados en la expresión algebraica, luego evalúe primero los exponentes.

\[ \begin{array}{l} (a^2 -b^2) \div (a+b) & = \left( \left( - \frac{1}{4} \right)^2 - \left( \frac{1}{2} \right)^2 \right) \div \left( \left( - \frac{1}{4} \right) + \left( \frac{1}{2} \right) \right) \\ ~ & = \left( \frac{1}{16} - \frac{1}{4} \right) \div \left( - \frac{1}{4} + \frac{1}{2} \right) \end{array}\nonumber \]

Debemos evaluar primero los paréntesis. Dentro de cada conjunto de paréntesis, cree fracciones equivalentes y realice restaciones y adiciones a continuación.

\[ \begin{array}{l} = \left( \frac{1}{16} - \frac{1 \cdot 4}{4 \cdot 4} \right) \div \left( - \frac{1}{4} + \frac{1 \cdot 2}{2 \cdot 2} \right) \\ = \left( \frac{1}{16} - \frac{4}{16} \right) \div \left( - \frac{1}{4} + \frac{2}{4} \right) \\ = - \frac{3}{16} \div \frac{1}{4} \end{array}\nonumber \]

Invertir y multiplicar.

\[ \begin{aligned} = - \frac{3}{16} \cdot \frac{4}{1} \\ = - \frac{12}{16} \end{aligned}\nonumber \]

Reducir.

\[ \begin{aligned} = - \frac{12 \div 4}{16 \div 4} \\ - \frac{3}{4} \end{aligned}\nonumber \]

Nota: En el último paso, también podrías reducir factorizando primos numerador y denominador y cancelando factores comunes.

Ejercicio

Dar a = −1/2 y b = −1/3, evaluar ab ÷ (a + b).

Contestar

−1/5

Fracciones Complejas

Fracciones Complejas

Cuando el numerador y denominador de una fracción contienen fracciones en sí mismas, tal expresión se denomina fracción compleja.

Puede utilizar el orden estándar de operaciones para simplificar una fracción compleja. Recordemos los consejos cuando una fracción está presente.

Expresiones fraccionarias

Si una expresión fraccionaria está presente, simplifique el numerador y el denominador por separado, luego divídalo.

Ejemplo 7

Simplificar:

\[ \frac{ - \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}}\nonumber \]

Solución

Tenemos suma en el numerador, resta en el denominador. En cada caso, necesitamos fracciones equivalentes con un denominador común.

\[ \begin{aligned} \frac{- \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}} = \frac{- \frac{1 \cdot \textcolor{red}{3}}{2 \cdot \textcolor{red}{3}} + \frac{1 \cdot \textcolor{red}{2}}{3 \cdot \textcolor{red}{2}}} ~ & \textcolor{red}{ \text{ Create equivalent fractions.}} \\ = \frac{- \frac{3}{6} + \frac{2}{6}}{ \frac{3}{4} - \frac{6}{4}} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \\ = \frac{- \frac{1}{6}}{- \frac{3}{4}} ~ & \textcolor{red}{ \begin{array}{l} ~ \text{ Numerator: } - \frac{3}{6} + \frac{2}{6} = - \frac{1}{6}. \\ \text{ Denominator: } \frac{3}{4} - \frac{6}{4} = - \frac{3}{4}. \end{array}} \end{aligned}\nonumber \]

La última expresión nos pide dividir. Invertir y multiplicar.

\[ \begin{aligned} = - \frac{1}{6} \div \left( - \frac{3}{4} \right) ~ & \textcolor{red}{ \text{ A complex fraction means divide.}} \\ = - \frac{1}{6} \cdot \left( - \frac{4}{3} \right) ~ & \textcolor{red}{ \text{ Invert and multiply.}} \end{aligned}\nonumber \]

Al igual que los signos (dos negativos) dan un producto positivo. Multiplicar numeradores y denominadores, luego reducir.

\[ \begin{aligned} = \frac{4}{18} ~ & \textcolor{red}{ \begin{array}{l} \text{ Like signs yields positive answer.} \\ \text{ Multiply numerators and denominators.} \end{array}} \\ = \frac{4 \div 2}{18 \div 2} ~ & \textcolor{red}{ \text{ Divide both numerator and denominator by 2.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Alternativamente, uno podría factor primo y cancelar para reducir a los términos más bajos; es decir,

\[ \begin{aligned} \frac{4}{18} = \frac{2 \cdot 2}{2\cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = \frac{ \cancel{2} \cdot 2}{ \cancel{2} \cdot 3 \cdot 3} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Ejercicio

Simplificar:

\[ \frac{ \frac{1}{4} - \frac{1}{3}}{ \frac{1}{4} + \frac{1}{3}}\nonumber \]

Contestar

−1/7

Despeje de fracciones

Se dispone de una técnica alternativa para simplificar fracciones complejas.

Borrar Fracciones de Fracciones Complejas

Puede borrar fracciones de una fracción compleja usando el siguiente algoritmo:

1. Determine un LCD1 para el numerador.
2. Determine un LCD2 para el denominador.
3. Determine una pantalla LCD tanto para LCD1 como para LCD2.
4. Multiplica tanto el numerador como el denominador por esta LCD “combinada”.

Apliquemos esta técnica a la fracción compleja del Ejemplo 7.

Ejemplo 8

Simplificar:

\[ \frac{- \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}}\nonumber \]

Solución

Como vimos en la solución del Ejemplo 7, se utilizaron denominadores comunes de 6 y 4 para el numerador y denominador, respectivamente. Así, un denominador común tanto para el numerador como para el denominador sería 12. Comenzamos la técnica de solución alternativa multiplicando tanto el numerador como el denominador por 12.

\[ \begin{aligned} \frac{ - \frac{1}{2} + \frac{1}{3}}{ \frac{3}{4} - \frac{3}{2}} = \frac{ \textcolor{red}{12} \left( - \frac{1}{2} + \frac{1}{3} \right)}{ \textcolor{red}{12} \left( \frac{3}{4} - \frac{3}{2} \right)} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 12.}} \\ = \frac{ \textcolor{red}{12} \left( - \frac{1}{2} \right) + \textcolor{red}{12} \left( \frac{1}{3} \right)}{ \textcolor{red}{12} \left( \frac{3}{4} \right) - \textcolor{red}{12} \left( \frac{3}{2} \right)} ~ & \textcolor{red}{ \text{ Distribute the 12.}} \\ = \frac{-6+4}{9-18} ~ & \textcolor{red}{ \begin{array}{l} \text{ Multiply: } 12(-1/2)=-6,~ 12(1/2) = 4. \\ 12(3/4)=9, \text{ and } 12(3/2)=18. \end{array}} \\ = \frac{-2}{-9} ~ & \textcolor{red}{ \text{ Simplify.}} \\ = \frac{2}{9} ~ & \textcolor{red}{ \text{ Like signs yield positive.}} \end{aligned}\nonumber \]

Ejercicio

Simplificar:\( \frac{- \frac{2}{3} + \frac{1}{5}}{ \frac{4}{5} - \frac{1}{2}}\)

Contestar

−14/9

Aplicación — Trapecio

Un trapecio es un tipo especial de cuadrilátero (polígono de cuatro lados).

Trapecio

Un cuadrilátero con un par de lados opuestos paralelos se llama trapecio.

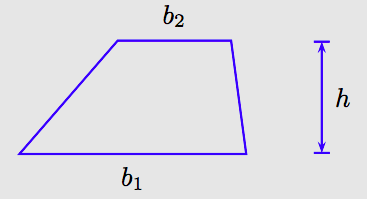
El par de lados paralelos se llaman las bases del trapecio. Sus longitudes están marcadas por las variables b ₁ y b ₂ en la figura anterior. La distancia entre las bases paralelas se denomina altura o altitud del trapecio. La altura está marcada por la variable h en la figura anterior.

Los matemáticos utilizan subíndices para crear nuevas variables. Así, b ₁ (“b sub 1”) y b ₂ (“b sub 2”) son dos variables distintas, utilizadas en este caso para representar la longitud de las bases del trapecio.

Al dibujar en diagonal, podemos dividir el trapecio en dos triángulos (ver Figura 4.14).

Figura 4.14: Dividiendo el trapecio en dos triángulos.

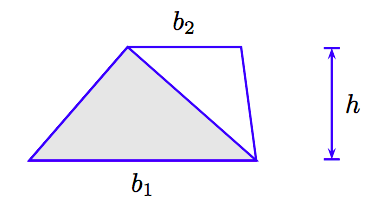
Podemos encontrar el área del trapecio sumando las áreas de los dos triángulos.

• El triángulo sombreado en la Figura 4.14 tiene base b ₁ y altura h. De ahí que el área del triángulo sombreado sea (1/2) b ₁ h.
• El triángulo sin sombra en la Figura 4.14 tiene base b ₂ y altura h. De ahí que el área del triángulo sin sombra sea (1/2) b ₂ h.

Sumando las áreas, el área del trapecio es

\[ \text{Area of Trapezoid} = \frac{1}{2} b_1h + \frac{1}{2} b_2h.\nonumber \]

Podemos utilizar la propiedad distributiva para factorizar a (1/2) h.

Área de un trapecio

Un trapecio con bases b ₁ y b ₂ y altura h tiene área

\[A = \frac{1}{2} h (b_1 + b_2).\nonumber \]

Es decir, para encontrar el área, sumar las bases, multiplicar por la altura, y tomar la mitad del resultado.

Ejemplo 9

Encuentra el área del trapecio que se muestra a continuación.

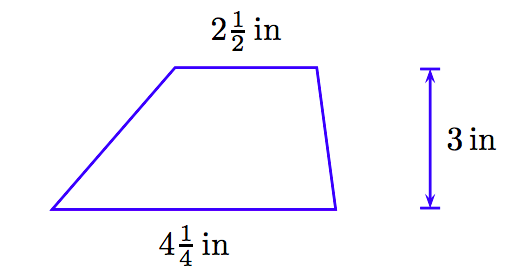
Solución

La fórmula para el área de un trapecio es

\[A = \frac{1}{2} h (b_1 + b_2)\nonumber \]

Sustituyendo las bases y la altura dadas, obtenemos

\[A = \frac{1}{2} (3) \left( 4 \frac{1}{4} + 2 \frac{1}{2} \right).\nonumber \]

Simplifique primero la expresión dentro de los paréntesis. Cambie las fracciones mixtas a fracciones impropias, haga fracciones equivalentes con un denominador común, luego agregue.

\[\begin{array}{c} A = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{5}{2} \right) \\ = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{5 \cdot 2}{2 \cdot 2} \right) \\ = \frac{1}{2} (3) \left( \frac{17}{4} + \frac{10}{4} \right) \\ = \frac{1}{2} \left( \frac{3}{1} \right) \left( \frac{27}{4} \right) \end{array}\nonumber \]

Multiplicar numeradores y denominadores.

\[ = \frac{81}{8}\nonumber \]

Esta fracción impropia es una respuesta perfectamente buena, pero cambiemos este resultado a una fracción mixta (81 dividido por 8 es 10 con un resto de 1). Así, el área del trapecio es

\[A = 10 \frac{1}{8} \text{ square inches.}\nonumber \]

Ejercicio

Un trapecio tiene bases que miden 6 y 15 pies, respectivamente. La altura del trapecio es de 5 pies. Encuentra el área del trapecio.

Contestar

\(52 \frac{1}{2} \text{ square feet}\)

Ejercicios

En los Ejercicios 1-8, simplificar la expresión.

1. \( \left( − \frac{7}{3} \right)^3\)

2. \( \left( \frac{1}{2} \right)^3\)

3. \( \left( \frac{5}{3} \right)^4\)

4. \( \left( − \frac{3}{5} \right)^4\)

5. \( \left( \frac{1}{2} \right)^5\)

6. \( \left( \frac{3}{4} \right)^5\)

7. \( \left( \frac{4}{3} \right)^2\)

8. \( \left( − \frac{8}{5} \right)^2\)

---

9. Si a = 7/6, evalúe un ³.

10. Si e = 1/6, evalúe e ³.

11. Si e = −2/3, evalúe − e ².

12. Si c = −1/5, evalúe − c ².

13. Si b = −5/9, evalúe b ².

14. Si c = 5/7, evalúe c ².

15. Si b = −1/2, evalúe − b ³.

16. Si a = −2/9, evalúe − a ³.

---

En los Ejercicios 17-36, simplificar la expresión.

17. \( \left( − \frac{1}{2} \right) \left( \frac{1}{6} \right) − \left( \frac{7}{8} \right) \left( − \frac{7}{9} \right)\)

18. \( \left( − \frac{3}{4} \right) \left( \frac{1}{2} \right) − \left( \frac{3}{5} \right) \left( \frac{1}{4} \right)\)

19. \( \left( − \frac{9}{8} \right)^2 − \left( − \frac{3}{2} \right) \left( \frac{7}{3} \right)\)

20. \( \left( \frac{3}{2} \right)^2 − \left( \frac{7}{8} \right) \left( − \frac{1}{2} \right)\)

21. \( \left( − \frac{1}{2} \right) \left( − \frac{7}{4} \right) − \left( − \frac{1}{2} \right)^2\)

22. \( \left( \frac{1}{5} \right) \left( − \frac{9}{4} \right) − \left( \frac{7}{4} \right)^2\)

23. \(− \frac{7}{6} − \frac{1}{7} \cdot \frac{7}{9}\)

24. \( − \frac{4}{9} − \frac{8}{5} \cdot \frac{8}{9}\)

25. \( \frac{3}{4} + \frac{9}{7} \left( − \frac{7}{6} \right)\)

26. \( \frac{3}{2} + \frac{1}{4} \left( − \frac{9}{8} \right)\)

27. \( \left( − \frac{1}{3} \right)^2 + \left( \frac{7}{8} \right) \left( − \frac{1}{3} \right)\)

28. \( \left( − \frac{2}{9} \right)^2 + \left( \frac{2}{3} \right) \left( \frac{1}{2} \right)\)

29. \(\frac{5}{9} + \frac{5}{9} \cdot \frac{7}{9}\)

30. \( − \frac{1}{2} + \frac{9}{8} \cdot \frac{1}{3}\)

31. \( \left( − \frac{5}{6} \right) \left( \frac{3}{8} \right) + \left( − \frac{7}{9} \right) \left( − \frac{3}{4} \right)\)

32. \( \left( \frac{7}{4} \right) \left( \frac{6}{5} \right) + \left( − \frac{2}{5} \right) \left( \frac{8}{3} \right)\)

33. \( \frac{4}{3} − \frac{2}{9} \left( − \frac{3}{4} \right)\)

34. \(− \frac{1}{3} − \frac{1}{5} \left( − \frac{4}{3} \right)\)

35. \( \left( − \frac{5}{9} \right) \left( \frac{1}{2} \right) + \left( − \frac{1}{6} \right)^2\)

36. \( \left( \frac{1}{4} \right) \left( \frac{1}{6} \right) + \left( − \frac{5}{6} \right)^2\)

---

37. Dado a = −5/4, b = 1/2, y c = 3/8, evaluar a + bc.

38. Dado a = −3/5, b = 1/5, y c = 1/3, evaluar a + bc.

39. Dado x = −1/8, y = 5/2, y z = −1/2, evaluar la expresión x + yz.

40. Dado x = −5/9, y = 1/4, y z = −2/3, evaluar la expresión x + yz.

41. Dado a = 3/4, b = 5/7, y c = 1/2, evaluar la expresión a − bc.

42. Dado a = 5/9, b = 2/3, y c = 2/9, evaluar la expresión a − bc.

43. Dado x = −3/2, y = 1/4, y z = −5/7, evalúe x ² − yz.

44. Dado x = −3/2, y = −1/2, y z = 5/3, evalúe x ² − yz.

45. Dado a = 6/7, b = 2/3, c = −8/9, y d = −6/7, evaluar ab + cd.

46. Dado a = 4/9, b = −3/2, c = 7/3, y d = −8/9, evaluar ab + cd.

47. Dado w = −1/8, x = −2/7, y = −1/2, y z = 8/7, evalúe wx − yz.

48. Dado w = 2/7, x = −9/4, y = −3/4, y z = −9/2, evalúe wx − yz.

49. Dado x = 3/8, y = 3/5, y z = −3/2, evalúe xy + z ².

50. Dado x = −1/2, y = 7/5, y z = −3/2, evalúe xy + z ².

51. Dado u = 9/7, v = 2/3 y w = −3/7, evalúe uv − w ².

52. Dado u = 8/7, v = −4/3, y w = 2/3, evaluar uv − w ².

53. Dado a = 7/8, b = −1/4, y c = −3/2, evaluar a ² + bc.

54. Dado a = −5/8, b = 3/2, y c = −3/2, evaluar a ² + bc.

55. Dado u = 1/3, v = 5/2 y w = −2/9, evalúe la expresión u − vw.

56. Dado u = −1/2, v = 1/4 y w = −1/4, evalúe la expresión u − vw.

---

En los Ejercicios 57-68, simplificar la compleja expresión racional.

57. \(\frac{ \frac{8}{3} + \frac{7}{6}}{− \frac{9}{2} − \frac{1}{4}}\)

58. \( \frac{ \frac{7}{8} + \frac{1}{9}}{ \frac{8}{9} − \frac{1}{6}}\)

59. \( \frac{ \frac{3}{4} + \frac{4}{3}}{ \frac{1}{9} + \frac{5}{3}}\)

60. \( \frac{− \frac{9}{8} − \frac{6}{5}}{ \frac{7}{4} + \frac{1}{2}}\)

61. \( \frac{ \frac{7}{5} + \frac{5}{2}}{− \frac{1}{4} + \frac{1}{2}}\)

62. \( \frac{ \frac{5}{6} + \frac{2}{3}}{ \frac{3}{5} + \frac{2}{3}}\)

63. \( \frac{− \frac{3}{2} − \frac{2}{3}}{− \frac{7}{4} − \frac{2}{3}}\)

64. \( \frac{ \frac{8}{9} + \frac{3}{4}}{− \frac{2}{3} − \frac{1}{6}}\)

65. \( \frac{− \frac{1}{2} − \frac{4}{7}}{− \frac{5}{7} + \frac{1}{6}}\)

66. \( \frac{− \frac{3}{2} − \frac{5}{8}}{ \frac{3}{4} − \frac{1}{2}}\)

67. \(\frac{− \frac{3}{7} − \frac{1}{3}}{ \frac{1}{3} − \frac{6}{7}}\)

68. \( \frac{− \frac{5}{8} − \frac{6}{5}}{− \frac{5}{4} − \frac{3}{8}}\)

---

69. Un trapecio tiene bases de medición\(3 \frac{3}{8}\) y\(5 \frac{1}{2}\) pies, respectivamente. La altura del trapecio es de 7 pies. Encuentra el área del trapecio.

70. Un trapecio tiene bases de medición\(2 \frac{1}{2}\) y\(6 \frac{7}{8}\) pies, respectivamente. La altura del trapecio es de 3 pies. Encuentra el área del trapecio.

71. Un trapecio tiene bases de medición\(2 \frac{1}{4}\) y\(7 \frac{3}{8}\) pies, respectivamente. La altura del trapecio es de 7 pies. Encuentra el área del trapecio.

72. Un trapecio tiene bases de medición\(3 \frac{1}{8}\) y\(6 \frac{1}{2}\) pies, respectivamente. La altura del trapecio es de 3 pies. Encuentra el área del trapecio.

73. Un trapecio tiene bases de medición\(2 \frac{3}{4}\) y\(6 \frac{5}{8}\) pies, respectivamente. La altura del trapecio es de 3 pies. Encuentra el área del trapecio.

74. Un trapecio tiene bases de medición\(2 \frac{1}{4}\) y\(7 \frac{1}{8}\) pies, respectivamente. La altura del trapecio es de 5 pies. Encuentra el área del trapecio.

---

RESPUESTAS

1. \(\frac{−343}{27}\)

3. \(\frac{625}{81}\)

5. \(\frac{1}{32}\)

7. \(\frac{16}{9}\)

9. \(\frac{343}{216}\)

11. \(\frac{−4}{9}\)

13. \(\frac{25}{81}\)

15. \(\frac{1}{8}\)

17. \(\frac{43}{72}\)

19. \(\frac{305}{64}\)

21. \(\frac{5}{8}\)

23. \(\frac{−23}{18}\)

25. \(\frac{−3}{4}\)

27. \(\frac{−13}{72}\)

29. \(\frac{80}{81}\)

31. \(\frac{13}{48}\)

33. \(\frac{3}{2}\)

35. \(\frac{−1}{4}\)

37. \(\frac{−17}{16}\)

39. \(\frac{−11}{8}\)

41. \(\frac{11}{28}\)

43. \(\frac{17}{7}\)

45. \(\frac{4}{3}\)

47. \(\frac{17}{28}\)

49. \(\frac{99}{40}\)

51. \(\frac{33}{49}\)

53. \(\frac{73}{64}\)

55. \(\frac{8}{9}\)

57. \(\frac{−46}{57}\)

59. \(\frac{75}{64}\)

61. \(\frac{78}{5}\)

63. \(\frac{26}{29}\)

65. \(\frac{45}{23}\)

67. \(\frac{16}{11}\)

69. \(31 \frac{1}{16}\)

71. \(33 \frac{11}{16}\)

73. \(14 \frac{1}{16}\)