Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

1.6: Restar números enteros (Parte 2)

Última actualización

30 oct 2022
Guardar como PDF
- 1.5: Restar números enteros (Parte 1)
- 1.7: Multiplicar números enteros (Parte 1)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Traducir frases de palabras a notación matemática

Al igual que con la suma, las frases de palabras pueden indicarnos que operemos en dos números usando la resta. Para traducir de una frase de palabras a notación matemática, buscamos palabras clave que indiquen sustracción. Algunas de las palabras que indican sustracción se listan en Tabla $\PageIndex{1}$ .

Mesa $\PageIndex{1}$
Operación	Frase de palabras	Ejemplo	Expresión
Resta	menos	5 menos 1	5 - 1
	diferencia	la diferencia de 9 y 4	9 - 4
	disminuyó en	7 disminuido en 3	7 - 3
	menos de	5 menos de 8	8 - 5
	restado de	1 restado de 6	6 - 1

Ejemplo $\PageIndex{11}$ : translate

Traduzca y luego simplifique:

la diferencia de $13$ y $8$
restar $24$ de $43$

Solución

La palabra diferencia nos dice que restemos los dos números. Los números permanecen en el mismo orden que en la frase.

	la diferencia de 13 y 8
Traducir.	13 - 8
Simplificar.	5

Las palabras restan de nos dice que quitemos el segundo número del primero. Debemos tener cuidado para que el orden sea correcto.

	restar 24 de 43
Traducir.	43 - 24
Simplificar.	19

Ejercicio $\PageIndex{21}$

Traducir y simplificar:

la diferencia de $14$ y $9$
restar $21$ de $37$

Responder a: $14-9=5$
Respuesta b: $37-21=16$

Ejercicio $\PageIndex{22}$

Traducir y simplificar:

$11$ disminuida en $6$
$18$ menos de $67$

Responder a: $11-6=5$
Respuesta b: $67-18=49$

Restar números enteros en aplicaciones

Para resolver aplicaciones con resta, usaremos el mismo plan que usamos con suma. Primero, tenemos que determinar qué se nos pide que encontremos. Entonces escribimos una frase que da la información para encontrarla. Traducimos la frase a notación matemática y luego simplificamos para obtener la respuesta. Por último, escribimos una oración para responder a la pregunta, utilizando las unidades correspondientes.

Ejemplo $\PageIndex{12}$ : difference

La temperatura en Chicago una mañana era de $73$ grados Fahrenheit. Llegó un frente frío y al mediodía la temperatura era de $27$ grados Fahrenheit. ¿Cuál era la diferencia entre la temperatura de la mañana y la temperatura al mediodía?

Solución

Se nos pide encontrar la diferencia entre la temperatura matutina y la temperatura del mediodía.

Escribe una frase.	la diferencia de 73 y 27
Traducir a notación matemática. La diferencia nos dice que restemos.	73 - 27
Entonces hacemos la resta.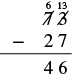
Escribe una oración para responder a la pregunta.	La diferencia de temperaturas fue de 46 grados Fahrenheit.

Ejercicio $\PageIndex{23}$

La alta temperatura de junio $1^{st}$ en Boston fue de $77$ grados Fahrenheit, y la baja temperatura fue de $58$ grados Fahrenheit. ¿Cuál fue la diferencia entre las temperaturas altas y bajas?

Responder: La diferencia es $19$ grados Fahrenheit.

Ejercicio $\PageIndex{24}$

El pronóstico del tiempo para junio $2^{nd}$ en San Luis predice una temperatura alta de $90$ grados Fahrenheit y una baja de $73$ grados Fahrenheit. ¿Cuál es la diferencia entre las temperaturas altas y bajas predichas?

Responder: La diferencia es $17$ grados Fahrenheit.

Ejemplo $\PageIndex{13}$ : difference

Se vende una lavadora para $$399$ . Su precio regular es $$588$ . ¿Cuál es la diferencia entre el precio regular y el precio de venta?

Solución

Se nos pide encontrar la diferencia entre el precio regular y el precio de venta.

Escribe una frase	la diferencia entre 588 y 399
Traducir a notación matemática	588 - 399
Restar
Escribe una oración para responder a la pregunta	La diferencia entre el precio regular y el precio de venta es de $189.

Ejercicio $\PageIndex{25}$

Un televisor está a la venta para $$499$ . Su precio regular es $$648$ . ¿Cuál es la diferencia entre el precio regular y el precio de venta?

Responder: La diferencia es $$149$ .

Ejercicio $\PageIndex{26}$

Un juego de patio está a la venta para $$149$ . Su precio regular es $$285$ . ¿Cuál es la diferencia entre el precio regular y el precio de venta?

Responder: La diferencia es $$136$ .

Acceda a recursos adicionales en línea

Conceptos clave

Operación	Notación	Expresión	Leer como	Resultado
Resta			siete menos tres	la diferencia de

Restar números enteros
- Escribe los números para que cada valor posicional se alingue verticalmente.
- Restar los dígitos en cada valor posicional. Trabajar de derecha a izquierda comenzando por el lugar de unos. Si el dígito de arriba es menor que el dígito de abajo, pida prestado según sea necesario.
- Continuar restando cada valor posicional de derecha a izquierda, tomando prestado si es necesario.
- Verifique agregando.

Glosario

diferencia: La diferencia es el resultado de restar dos o más números.

La práctica hace la perfección

Usar notación de resta

En los siguientes ejercicios, traduzca de la notación matemática a las palabras.

15 - 9
18 - 16
42 - 35
83 - 64
675 - 350
790 - 525

Modelo de resta de números enteros

En los siguientes ejercicios, modele la resta.

5 - 2
8 - 4
6 - 3
7 - 5
18 - 5
19 - 8
17 - 8
17 - 9
35 - 13
32 - 11
61 - 47
55 - 36

Restar números enteros

En los siguientes ejercicios, restar y luego verificar sumando.

9 - 4
9 - 3
8 - 0
2 - 0
38 - 16
45 - 21
85 - 52
99 - 47
493 - 370
268 - 106
5,946 - 4,625
7,775 - 3,251
75 - 47
63 - 59
461 - 239
486 - 257
525 - 179
542 - 288
6,318 - 2,799
8,153 - 3,978
2,150 - 964
4,245 - 899
43,650 - 8,982
35,162 - 7,885

Traducir frases de palabras a expresiones algebraicas

En los siguientes ejercicios, traduzca y simplifique.

La diferencia de 10 y 3
La diferencia de 12 y 8
La diferencia de 15 y 4
La diferencia de 18 y 7
Restar 6 de 9
Restar 8 de 9
Restar 28 de 75
Restar 59 de 81
45 disminuido en 20
37 disminuidos en 24
92 disminuidos en 67
75 disminuidos en 49
12 menos de 16
15 menos de 19
38 menos de 61
47 menos de 62

Práctica Mixta

En los siguientes ejercicios, simplifique.

76−47
91 − 53
256 − 184
305 − 262
719 + 341
647 + 528
2,015 − 1,993
2,020 − 1,984

En los siguientes ejercicios, traduzca y simplifique.

Setenta y cinco más de treinta y cinco
Sesenta más de noventa y tres
13 menos de 41
28 menos de 36
La diferencia de 100 y 76
La diferencia de 1,000 y 945

Restar números enteros en aplicaciones

En los siguientes ejercicios, resuelve.

Temperatura La temperatura alta del 2 de junio en Las Vegas fue de 80 grados y la temperatura baja fue de 63 grados. ¿Cuál fue la diferencia entre las temperaturas altas y bajas?
Temperatura La temperatura alta del 1 de junio en Phoenix fue de 97 grados y la baja fue de 73 grados. ¿Cuál fue la diferencia entre las temperaturas altas y bajas?
Tamaño de la clase La clase de tercer grado de Olivia tiene 35 hijos. El año pasado, su clase de segundo grado tuvo 22 hijos. ¿Cuál es la diferencia entre el número de niños en la clase de tercer grado de Olivia y su clase de segundo grado?
Tamaño de la clase Hay 82 alumnos en la banda escolar y 46 en la orquesta escolar. ¿Cuál es la diferencia entre el número de alumnos en la banda y la orquesta?
Compras Una bicicleta de montaña está a la venta por $399. Su precio regular es de 650 dólares. ¿Cuál es la diferencia entre el precio regular y el precio de venta?
Compras Un juego de colchones está a la venta por $755. Su precio regular es de $1,600. ¿Cuál es la diferencia entre el precio regular y el precio de venta?
Ahorros John quiere comprar una computadora portátil que cuesta $840. Tiene 685 dólares en su cuenta de ahorros. ¿Cuánto más necesita ahorrar para poder comprar el portátil?
Mason Bancario tenía $1,125 en su cuenta corriente. Gastó 892 dólares. ¿Cuánto dinero le queda?

Matemáticas cotidianas

Viaje por carretera Noah conducía de Filadelfia a Cincinnati, a una distancia de 502 millas. Condujo 115 millas, se detuvo por gasolina, y luego condujo otras 230 millas antes del almuerzo. ¿Cuántas millas más tenía que recorrer?
Puntajes de las pruebas Sara necesita 350 puntos para aprobar su curso. Ella anotó 75, 50, 70 y 80 en sus primeras cuatro pruebas. ¿Cuántos puntos más necesita Sara para aprobar el curso?

Ejercicios de escritura

Explicar cómo se relacionan la resta y la suma.
¿Cómo te ayuda conocer los hechos de suma a restar números?

Autocomprobación

(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección

(b) ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?

Colaboradores y Atribuciones

Template:ContribElementaryAlgebraOpenStax

Traducir frases de palabras a notación matemática

Ejemplo1.6.11\PageIndex{11}: translate

Ejercicio1.6.21\PageIndex{21}

Ejercicio1.6.22\PageIndex{22}

Restar números enteros en aplicaciones

Ejemplo1.6.12\PageIndex{12}: difference

Ejercicio1.6.23\PageIndex{23}

Ejercicio1.6.24\PageIndex{24}

Ejemplo1.6.13\PageIndex{13}: difference

Ejercicio1.6.25\PageIndex{25}

Ejercicio1.6.26\PageIndex{26}

Acceda a recursos adicionales en línea

Conceptos clave

Glosario

La práctica hace la perfección

Usar notación de resta

Modelo de resta de números enteros

Restar números enteros

Traducir frases de palabras a expresiones algebraicas

Práctica Mixta

Restar números enteros en aplicaciones

Matemáticas cotidianas

Ejercicios de escritura

Autocomprobación

Colaboradores y Atribuciones

Support Center

How can we help?

Ejemplo $\PageIndex{11}$ : translate

Ejercicio $\PageIndex{21}$

Ejercicio $\PageIndex{22}$

Ejemplo $\PageIndex{12}$ : difference

Ejercicio $\PageIndex{23}$

Ejercicio $\PageIndex{24}$

Ejemplo $\PageIndex{13}$ : difference

Ejercicio $\PageIndex{25}$

Ejercicio $\PageIndex{26}$