1.9: Dividir números enteros (Parte 1)
- Page ID
- 114214
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Usar notación de división
- Modelo de división de números enteros
- Dividir números enteros
- Traducir frases de palabras a notación matemática
- Dividir números enteros en aplicaciones
Antes de comenzar, toma este cuestionario de preparación.
- Multiplicar:\(27 • 3\). Si te perdiste este problema, revisa el Ejemplo 1.4.6.
- Restar:\(43 − 26\). Si te perdiste este problema, revisa el Ejemplo 1.3.4.
- Multiplicar:\(62(87)\). Si te perdiste este problema, revisa el Ejemplo 1.4.8.
Usar notación de división
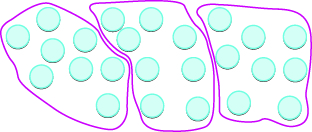
Hasta ahora hemos explorado la suma, resta y multiplicación. Ahora consideremos la división. Supongamos que tiene las\(12\) galletas en Figura\(\PageIndex{1}\) y quiere empaquetarlas en bolsas con\(4\) galletas en cada bolsa. ¿Cuántas bolsas necesitaríamos?

Figura\(\PageIndex{1}\)
Podrías poner\(4\) galletas en la primera bolsa,\(4\) en la segunda bolsa, y así sucesivamente hasta que te quedes sin galletas. Haciéndolo de esta manera, llenarías\(3\) bolsas.

Figura\(\PageIndex{2}\)
Es decir, a partir de las\(12\) cookies, quitarías, o restarías,\(4\) las cookies a la vez. La división es una forma de representar la resta repetida del mismo modo que la multiplicación representa la suma repetida. En lugar de restar\(4\) repetidamente, podemos escribir
\[12 \div 4 \nonumber \]
Leemos esto como doce dividido por cuatro y el resultado es el cociente de\(12\) y\(4\). El cociente es\(3\) porque podemos restar\(12\) exactamente\(4\) de\(3\) tiempos. Llamamos al número que se divide el dividendo y al número que lo divide el divisor. En este caso, el dividendo es\(12\) y el divisor es\(4\). En el pasado es posible que hayas usado la notación\(4 \overline{\smash{)}12}\), pero esta división también se puede escribir como\(12 ÷ 4\),\(12/4\),\(\dfrac{12}{4}\). En cada caso el\(12\) es el dividendo y el\(4\) es el divisor.
Para representar y describir la división, podemos usar símbolos y palabras.
| Operación | Notación | Expresión | Leer como | Resultado |
|---|---|---|---|---|
| División | ÷ | 12 ÷ 4 | Doce dividido por cuatro | el cociente de 12 y 4 |
| \(\dfrac{a}{b}\) | \(\dfrac{12}{4}\) | |||
| \(b \overline{)a}\) | \(4 \overline{\smash{)}12}\) | |||
| a/b | 12/4 |
La división se realiza en dos números a la vez. Cuando traduzca de notación matemática a palabras en inglés, o palabras en inglés a notación matemática, busque las palabras de y y para identificar los números.
Traducir de la notación matemática a las palabras.
- \(64 ÷ 8\)
- \(\dfrac{42}{7}\)
- \(4 \overline{\smash{)}28}\)
Solución
- Leemos esto como sesenta y cuatro dividido por ocho y el resultado es el cociente de sesenta y cuatro y ocho.
- Leemos esto como cuarenta y dos dividido por siete y el resultado es el cociente de cuarenta y dos y siete.
- Leemos esto como veintiocho dividido por cuatro y el resultado es el cociente de veintiocho y cuatro.
Traducir de la notación matemática a las palabras:
- \(84 ÷ 7\)
- \(\dfrac{18}{6}\)
- \(8 \overline{\smash{)}24}\)
- Responder a
-
ochenta y cuatro dividido por siete; el cociente de ochenta y cuatro y siete
- Respuesta b
-
dieciocho dividido por seis; el cociente de dieciocho y seis.
- Respuesta c
-
veinticuatro dividido por ocho; el cociente de veinticuatro y ocho
Traducir de la notación matemática a las palabras:
- \(72÷ 9\)
- \(\dfrac{21}{3}\)
- \(6 \overline{\smash{)}54}\)
- Responder a
-
setenta y dos divididos por nueve; el cociente de setenta y dos y nueve
- Respuesta b
-
veintiuno dividido por tres; el cociente de veintiuno y tres
- Respuesta c
-
cincuenta y cuatro dividido por seis; el cociente de cincuenta y cuatro y seis
División Modelo de Números Enteros
Como hicimos con la multiplicación, modelaremos la división usando contadores. La operación de división nos ayuda a organizar los artículos en grupos iguales ya que comenzamos con el número de elementos en el dividendo y restamos el número en el divisor repetidamente.
Modelar la división:\(24 ÷ 8\).
Solución
Para encontrar el cociente\(24 ÷ 8\), queremos saber cuántos grupos de\(8\) están en\(24\).
Modelar el dividendo. Comience con\(24\) mostradores.

El divisor nos dice el número de contadores que queremos en cada grupo. Formar grupos de\(8\) contadores.
Contar el número de grupos. Hay\(3\) grupos.
\[24 \div 8 = 3 \nonumber\]
Modelo:\(24 ÷ 6\).
- Contestar
-
Modelo:\(42 ÷ 7\).
- Contestar
-
Dividir números enteros
Dijimos que la suma y la resta son operaciones inversas porque una deshace la otra. De igual manera, la división es la operación inversa de multiplicación. Sabemos\(12 ÷ 4 = 3\) porque\(3 • 4 = 12\). Conocer todos los hechos del número de multiplicación es muy importante a la hora de hacer división.
Comprobamos nuestra respuesta a la división multiplicando el cociente por el divisor para determinar si es igual al dividendo. En Ejemplo\(\PageIndex{2}\), sabemos que\(24 ÷ 8 = 3\) es correcto porque\(3 • 8 = 24\).
Dividir. Después verifica multiplicando.
- \(42 ÷ 6\)
- \(\dfrac{72}{9}\)
- \(7 \overline{\smash{)}63}\)
Solución
| Divide 42 por 6. | 42 ÷ 6 = 7 |
| Verificar multiplicando. | 7 • 6 = 42 ✓ |
| Divide 72 por 9. | \(\dfrac{72}{9}\) |
| Verificar multiplicando. | 8 • 9 = 72 ✓ |
| Divide 63 por 7. | \(7 \overline{\smash{)}63}\) |
| Verificar multiplicando. | 9 • 7 = 63 ✓ |
Dividir. Luego verifique multiplicando:
- \(54 ÷ 6\)
- \(\dfrac{27}{9}\)
- Responder a
-
\(9\)
- Respuesta b
-
\(3\)
Dividir. Luego verifique multiplicando:
- \(\dfrac{36}{9}\)
- \(8 \overline{\smash{)}40}\)
- Responder a
-
\(4\)
- Respuesta b
-
\(5\)
¿Cuál es el cociente cuando se divide un número por sí mismo?
\[\dfrac{15}{15} = 1 \quad \text{because} \quad 1 \cdot 15 = 15 \nonumber \]
Dividir cualquier número (excepto\(0\)) por sí mismo produce un cociente de\(1\). Además, cualquier número dividido por\(1\) produce un cociente del número. Estas dos ideas están plasmadas en la División Propiedades de Uno.
| Cualquier número (excepto 0) dividido por sí mismo es uno. | a ÷ a = 1 |
| Cualquier número dividido por uno es el mismo número. | a ÷ 1 = a |
Dividir. Luego verifique multiplicando:
- \(11 ÷ 11\)
- \(\dfrac{19}{1}\)
- \(1 \overline{\smash{)}7}\)
Solución
| Un número dividido por sí mismo es 1. | 11 ÷ 11 = 1 |
| Verificar multiplicando. | 1 • 11 = 11 ✓ |
| Un número dividido por 1 se iguala a sí mismo. | \(\dfrac{19}{1} = 19\) |
| Verificar multiplicando. | 19 • 1 = 19 ✓ |
| Un número dividido por 1 se iguala a sí mismo. | \(1 \overline{\smash{)}7} = 7\) |
| Verificar multiplicando. | 7 • 1 = 7 ✓ |
Dividir. Luego verifique multiplicando:
- \(14 ÷ 14\)
- \(\dfrac{27}{1}\)
- Responder a
-
\(1\)
- Respuesta b
-
\(27\)
Dividir. Luego verifique multiplicando:
- \(\dfrac{16}{1}\)
- \(1 \overline{\smash{)}4}\)
- Responder a
-
\(16\)
- Respuesta b
-
\(4\)
Supongamos que tenemos\($0\), y queremos dividirlo entre\(3\) las personas. ¿Cuánto obtendría cada persona? Cada persona obtendría\($0\). Cero dividido por cualquier número es\(0\).
Ahora supongamos que queremos dividir\($10\) por\(0\). Eso significa que nos gustaría encontrar un número por el que multiplicamos\(0\) para obtener\(10\). Esto no puede suceder porque\(0\) veces cualquier número es\(0\). Se dice que la división por cero es indefinida.
Estas dos ideas conforman las Propiedades de División de Cero.
| El cero dividido por cualquier número es 0. | 0 ÷ a = 0 |
| Dividir un número por cero no está definido. | a ÷ 0 = indefinido |
Otra forma de explicar por qué la división por cero es indefinida es recordar que la división es realmente resta repetida. ¿De cuántas veces podemos\(0\) quitarle\(10\)? Porque restar nunca\(0\) cambiará el total, nunca obtendremos una respuesta. Entonces no podemos dividir un número por\(0\).
Dividir. Verifica multiplicando:
- \(0 ÷ 3\)
- \(10 / 0\)
Solución
| El cero dividido por cualquier número es cero. | 0 ÷ 3 = 0 |
| Verificar multiplicando. | 0 • 3 = 0 ✓ |
| Dividir un número por cero no está definido. | 10/0 = indefinido |
Dividir. Luego verifique multiplicando:
- \(0 ÷ 2\)
- \(17 / 0\)
- Responder a
-
\(0\)
- Respuesta b
-
undefined
Dividir. Luego verifique multiplicando:
- \(0 ÷ 6\)
- \(13 / 0\)
- Responder a
-
\(0\)
- Respuesta b
-
undefined
Cuando el divisor o el dividendo tiene más de un dígito, suele ser más fácil usar la\(4 \overline{\smash{)}12}\) notación. Este proceso se llama división larga. Trabajemos a través del proceso dividiéndolo\(78\) por\(3\).
| Dividir el primer dígito del dividendo, 7, por el divisor, 3. | |
| El divisor 3 puede entrar en 7 dos veces ya que 2 × 3 = 6. Escribe los 2 arriba del 7 en el cociente. | 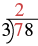 |
| Multiplique el 2 en el cociente por 3 y escriba el producto, 6, debajo del 7. |  |
| Restar ese producto del primer dígito del dividendo. Restar 7 − 6. Escribe la diferencia, 1, debajo del primer dígito del dividendo. |  |
| Bajar el siguiente dígito del dividendo. Derriba el 8. | 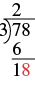 |
| Divida 18 por el divisor, 3. El divisor 3 entra en 18 seis veces. | 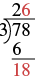 |
| Escribe 6 en el cociente por encima del 8. | |
| Multiplique el 6 en el cociente por el divisor y escriba el producto, 18, debajo del dividendo. Restar 18 de 18. |  |
Repetiríamos el proceso hasta que no haya más dígitos en el dividendo para derribar. En este problema, no hay más dígitos para derribar, por lo que la división está terminada. Entonces\(78 ÷ 3 = 26\).
Verifique multiplicando el cociente por el divisor para obtener el dividendo. \(26 × 3\)Multiplicar para asegurarse de que el producto es igual al dividendo,\(78\).

Lo hace, así que nuestra respuesta es correcta.
Paso 1. Dividir el primer dígito del dividendo por el divisor. Si el divisor es mayor que el primer dígito del dividendo, divida los dos primeros dígitos del dividendo por el divisor, y así sucesivamente.
Paso 2. Escribe el cociente por encima del dividendo.
Paso 3. Multiplique el cociente por el divisor y escriba el producto bajo el dividendo.
Paso 4. Restar ese producto del dividendo.
Paso 5. Bajar el siguiente dígito del dividendo.
Paso 6. Repita desde el Paso 1 hasta que no haya más dígitos en el dividendo para derribar.
Paso 7. Verifique multiplicando el cociente por el divisor.
Dividir\(2,596 ÷ 4\). Verificar multiplicando.
Solución
| Vamos a reescribir el problema para configurarlo para división larga. | 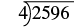 |
| Dividir el primer dígito del dividendo, 2, por el divisor, 4. |  |
| Dado que 4 no entra en 2, utilizamos los dos primeros dígitos del dividendo y dividimos 25 por 4. El divisor 4 entra en 25 seis veces. | |
| Escribimos el 6 en el cociente por encima del 5. |  |
| Multiplique el 6 en el cociente por el divisor 4 y escriba el producto, 24, debajo de los dos primeros dígitos del dividendo. |  |
| Restar ese producto de los dos primeros dígitos del dividendo. Restar 25 − 24. Escribe la diferencia, 1, debajo del segundo dígito en el dividendo. | 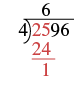 |
| Ahora baja el 9 y repite estos pasos. Hay 4 cuatros en 19. Escribe el 4 sobre el 9. Multiplica el 4 por 4 y resta este producto de 19. | 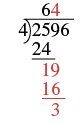 |
| Baje el 6 y repita estos pasos. Hay 9 cuatros en 36. Escribe el 9 sobre el 6. Multiplica el 9 por 4 y resta este producto de 36. |  |
| Verificar multiplicando. | 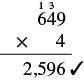 |
Es igual al dividendo, por lo que nuestra respuesta es correcta. Entonces\(2,596 ÷ 4 = 649\).
Dividir. Después verifique multiplicando:\(2,636 ÷ 4\).
- Contestar
-
\(659\)
Dividir. Después verifique multiplicando:\(2,716 ÷ 4\).
- Contestar
-
\(679\)
Dividir\(4,506 ÷ 6\). Verificar multiplicando.
Solución
| Vamos a reescribir el problema para configurarlo para división larga. |  |
| Primero tratamos de dividir 6 en 4. |  |
| Como eso no va a funcionar, intentamos 6 en 45. Hay 7 seis en 45. Escribimos el 7 sobre el 5 |  |
| Multiplica el 7 por 6 y resta este producto de 45. |  |
| Ahora baja el 0 y repite estos pasos. Hay 5 seis en 30. Escribe el 5 sobre el 0. Multiplica el 5 por 6 y resta este producto de 30. |  |
| Ahora baja el 6 y repite estos pasos. Hay 1 seis en 6. Escribe el 1 sobre el 6. Multiplica 1 por 6 y resta este producto de 6. |  |
| Verificar multiplicando. |  |
Es igual al dividendo, por lo que nuestra respuesta es correcta.
Dividir. Después verifique multiplicando:\(4,305 ÷ 5\).
- Contestar
-
\(861\)
Dividir. Después verifique multiplicando:\(3,906 ÷ 6\).
- Contestar
-
\(651\)
Dividir\(7,263 ÷ 9\). Verificar multiplicando.
Solución
| Vamos a reescribir el problema para configurarlo para división larga. |  |
| Primero tratamos de dividir 9 en 7. |  |
| Como eso no va a funcionar, intentamos 9 en 72. Hay 8 nueves en 72. Escribimos el 8 sobre el 2. |  |
| Multiplica el 8 por 9 y resta este producto del 72. |  |
| Ahora baja el 6 y repite estos pasos. Hay 0 nueves en 6. Escribe el 0 sobre el 6. Multiplica el 0 por 9 y resta este producto del 6. |  |
| Ahora baja el 3 y repite estos pasos. Hay 7 nueves en 63. Escribe el 7 sobre el 3. Multiplica el 7 por 9 y resta este producto de 63. |  |
| Verificar multiplicando. |  |
Es igual al dividendo, por lo que nuestra respuesta es correcta.
Dividir. Después verifique multiplicando:\(4,928 ÷ 7\).
- Contestar
-
\(704\)
Dividir. Después verifique multiplicando:\(5,663 ÷ 7\).
- Contestar
-
\(809\)
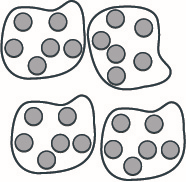
Hasta el momento todos los problemas de división han funcionado de manera uniforme. Por ejemplo, si tuviéramos\(24\) galletas y quisiéramos hacer bolsas de\(8\) galletas, tendríamos\(3\) bolsas. Pero, ¿y si hubiera\(28\) galletas y quisiéramos hacer bolsas de\(8\)? Comience con las\(28\) cookies como se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\)
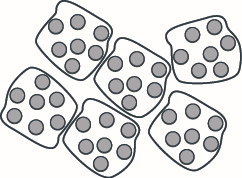
Trate de poner las galletas en grupos de ocho como en la Figura\(\PageIndex{4}\).
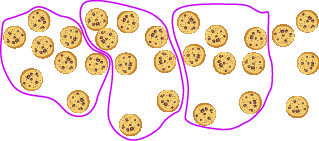
Figura\(\PageIndex{4}\)
Hay\(3\) grupos de ocho galletas, y\(4\) las cookies sobran. Llamamos a las\(4\) cookies que quedan sobre el resto y lo mostramos escribiendo\(R4\) junto a la\(3\). (Las\(R\) siglas para el resto.)
Para verificar esta división multiplicamos\(8\) los\(3\) tiempos para obtener\(24\), y luego sumar el resto de\(4\).

Dividir\(1,439 ÷ 4\). Verificar multiplicando.
Solución
| Vamos a reescribir el problema para configurarlo para división larga. |  |
| Primero tratamos de dividir 4 en 1. Como eso no va a funcionar, intentamos 4 en 14. Hay 3 cuatros en 14. Escribimos el 3 sobre el 4. |  |
| Multiplica el 3 por 4 y resta este producto de 14. |  |
| Ahora baja el 3 y repite estos pasos. Hay 5 cuatros en 23. Escribe el 5 sobre el 3. Multiplica el 5 por 4 y resta este producto de 23. |  |
| Ahora baja el 9 y repite estos pasos. Hay 9 cuatros en 39. Escribe el 9 sobre el 9. Multiplica el 9 por 4 y resta este producto de 39. No hay más números que derribar, así que ya terminamos. El resto es 3. |  |
| Verificar multiplicando. |  |
Así\(1,439 ÷ 4\) es\(359\) con un resto de\(3\). Nuestra respuesta es correcta.
Dividir. Después verifique multiplicando:\(3,812 ÷ 8\).
- Contestar
-
\(476\)con un resto de\(4\)
Dividir. Después verifique multiplicando:\(4,319 ÷ 8\).
- Contestar
-
\(539\)con un resto de\(7\)
Dividir y luego verificar multiplicando:\(1,461 ÷ 13\).
Solución
| Vamos a reescribir el problema para configurarlo para división larga. |  |
| Primero tratamos de dividir 13 en 1. Como eso no va a funcionar, intentamos 13 en 14. Hay 1 trece de cada 14. Escribimos el 1 sobre el 4. |  |
| Multiplica el 1 por 13 y resta este producto de 14. |  |
| Ahora baja el 6 y repite estos pasos. Hay 1 trece de cada 16. Escribe el 1 sobre el 6. Multiplica el 1 por 13 y resta este producto de 16. |  |
| Ahora baja el 1 y repite estos pasos. Hay 2 trece en 31. Escribe el 2 sobre el 1. Multiplica el 2 por 13 y resta este producto de 31. No hay más números que derribar, así que ya terminamos. El resto es 5. 1,462 ÷ 13 es 112 con un resto de 5. | 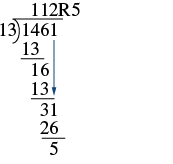 |
| Verificar multiplicando. |  |
Nuestra respuesta es correcta.
Dividir. Después verifique multiplicando:\(1,493 ÷ 13\).
- Contestar
-
\(114\)R\(11\)
Dividir. Después verifique multiplicando:\(1,461 ÷ 12\).
- Contestar
-
\(121\)R\(9\)
Dividir y verificar multiplicando:\(74,521 ÷ 241\).
Solución
| Vamos a reescribir el problema para configurarlo para división larga. |  |
| Primero tratamos de dividir 241 en 7. Como eso no va a funcionar, intentamos 241 en 74. Eso todavía no va a funcionar, así que intentamos 241 en 745. Ya que 2 se divide en 7 tres veces, intentamos 3. Desde 3 × 241 = 723, escribimos el 3 sobre el 5 en 745. Tenga en cuenta que 4 sería demasiado grande porque 4 × 241 = 964, que es mayor que 745. | |
| Multiplica el 3 por 241 y resta este producto de 745. |  |
| Ahora baja el 2 y repite estos pasos. 241 no divide en 222. Escribimos un 0 sobre el 2 como marcador de posición y luego continuamos. |  |
| Ahora baja el 1 y repite estos pasos. Prueba 9. Desde 9 × 241 = 2,169, escribimos el 9 sobre el 1. Multiplica el 9 por 241 y resta este producto de 2,221. |  |
| No hay más números que derribar, así que estamos acabados. El resto es de 52. Entonces 74,521 ÷ 241 es 309 con un resto de 52. | |
| Verificar multiplicando. |  |
A veces puede que no sea obvio cuántas veces el divisor entra en dígitos del dividendo. Tendremos que adivinar y verificar los números para encontrar el mayor número que entre en los dígitos sin superarlos.
Dividir. Después verifique multiplicando:\(78,641 ÷ 256\).
- Contestar
-
\(307\)R\(49\)
Dividir. Después verifique multiplicando:\(76,461 ÷ 248\).
- Contestar
-
\(308\)R\(77\)


