4.3: Multiplicar y dividir fracciones (Parte 1)
- Page ID
- 114240
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Simplificar fracciones
- Multiplicar fracciones
- Encuentra reciprocales
- Dividir fracciones
Antes de comenzar, toma este cuestionario de preparación.
- Encuentra la factorización principal de\(48\). Si te perdiste este problema, revisa el Ejemplo 2.5.1.
- Dibuja un modelo de la fracción\(\dfrac{3}{4}\). Si te perdiste este problema, revisa el Ejemplo 4.1.2.
- Encuentra dos fracciones equivalentes a\(\dfrac{5}{6}\). Las respuestas pueden variar. Las respuestas aceptables incluyen\(\dfrac{10}{12}, \dfrac{15}{18}, \dfrac{50}{60}\), etc. Si te perdiste este problema, revisa Ejemplo 4.1.14.
Simplificar fracciones
Al trabajar con fracciones equivalentes, viste que hay muchas formas de escribir fracciones que tienen el mismo valor, o representan la misma parte del todo. ¿Cómo sabes cuál usar? A menudo, usaremos la fracción que está en forma simplificada.
Una fracción se considera simplificada si no hay factores comunes, distintos a\(1\), en el numerador y denominador. Si una fracción tiene factores comunes en el numerador y denominador, podemos reducir la fracción a su forma simplificada eliminando los factores comunes.
Una fracción se considera simplificada si no hay factores comunes en el numerador y denominador.
Por ejemplo,
- \(\dfrac{2}{3}\)se simplifica porque no hay factores comunes de\(2\) y\(3\).
- \(\dfrac{10}{15}\)no se simplifica porque\(5\) es un factor común de\(10\) y\(15\).
El proceso de simplificar una fracción a menudo se llama reducir la fracción. En la sección anterior, utilizamos la Propiedad de Fracciones Equivalentes para encontrar fracciones equivalentes. También podemos usar la Propiedad de Fracciones Equivalentes a la inversa para simplificar fracciones. Reescribimos la propiedad para mostrar ambas formas juntas.
Si\(a, b, c\) son los números donde\(b ≠ 0, c ≠ 0\), entonces\(\dfrac{a}{b} = \dfrac{a \cdot c}{b \cdot c}\) y\(\dfrac{a \cdot c}{b \cdot c} = \dfrac{a}{b}\).
Observe que\(c\) es un factor común en el numerador y denominador. Siempre que tengamos un factor común en el numerador y denominador, se puede eliminar.
Paso 1. Reescribir el numerador y denominador para mostrar los factores comunes. Si es necesario, factoriza el numerador y el denominador en números primos.
Paso 2. Simplifique, usando la propiedad de fracciones equivalentes, eliminando factores comunes.
Paso 3. Multiplique cualquier factor restante.
Simplificar:\(\dfrac{10}{15}\).
Solución
Para simplificar la fracción, buscamos cualquier factor común en el numerador y el denominador.
| Observe que 5 es un factor tanto de 10 como de 15. | \(\dfrac{10}{15}\) |
| Factorizar el numerador y el denominador. | \(\dfrac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}}\) |
| Eliminar los factores comunes. | \(\dfrac{2 \cdot \cancel{\textcolor{red}{5}}}{3 \cdot \cancel{\textcolor{red}{5}}}\) |
| Simplificar. | \(\dfrac{2}{3}\) |
Simplificar:\(\dfrac{8}{12}\).
- Contestar
-
\(\dfrac{2}{3}\)
Simplificar:\(\dfrac{12}{16}\).
- Contestar
-
\(\dfrac{3}{4}\)
Para simplificar una fracción negativa, utilizamos el mismo proceso que en Ejemplo\(\PageIndex{1}\). Recuerda mantener el signo negativo.
Simplificar:\(− \dfrac{18}{24}\).
Solución
| Notamos que 18 y 24 ambos tienen factores de 6. | \(- \dfrac{18}{24}\) |
| Reescribir el numerador y denominador mostrando el factor común. | \(- \dfrac{3 \cdot \textcolor{red}{6}}{4 \cdot \textcolor{red}{6}}\) |
| Eliminar factores comunes. | \(- \dfrac{3 \cdot \cancel{\textcolor{red}{6}}}{4 \cdot \cancel{\textcolor{red}{6}}}\) |
| Simplificar. | \(- \dfrac{3}{4}\) |
Simplificar:\(− \dfrac{21}{28}\).
- Contestar
-
\(-\dfrac{3}{4}\)
Simplificar:\(− \dfrac{16}{24}\).
- Contestar
-
\(-\dfrac{2}{3}\)
Después de simplificar una fracción, siempre es importante verificar el resultado para asegurarse de que el numerador y el denominador no tengan más factores en común. Recuerde, la definición de una fracción simplificada: una fracción se considera simplificada si no hay factores comunes en el numerador y denominador.
Al simplificar una fracción impropia, no hay necesidad de cambiarla a un número mixto.
Simplificar:\(− \dfrac{56}{32}\).
Solución
| \(- \dfrac{56}{32}\) | |
| Reescribir el numerador y denominador, mostrando los factores comunes, 8. | \(- \dfrac{7 \cdot \textcolor{red}{8}}{4 \cdot \textcolor{red}{8}}\) |
| Eliminar factores comunes. | \(- \dfrac{7 \cdot \cancel{\textcolor{red}{8}}}{4 \cdot \cancel{\textcolor{red}{8}}}\) |
| Simplificar. | \(- \dfrac{7}{4}\) |
Simplificar:\(− \dfrac{54}{42}\).
- Contestar
-
\(-\dfrac{9}{7}\)
Simplificar:\(− \dfrac{81}{45}\).
- Contestar
-
\(-\dfrac{9}{5}\)
Paso 1. Reescribir el numerador y denominador para mostrar los factores comunes. Si es necesario, factoriza el numerador y el denominador en números primos.
Paso 2. Simplifique, usando la propiedad de fracciones equivalentes, eliminando factores comunes.
Paso 3. Multiplique cualquier factor restante.
A veces puede que no sea fácil encontrar factores comunes del numerador y denominador. Una buena idea, entonces, es facturar el numerador y el denominador en números primos. (Es posible que desee utilizar el método de árbol de factores para identificar los factores primos). Luego divida los factores comunes usando la Propiedad de Fracciones Equivalentes.
Simplificar:\(\dfrac{210}{385}\).
Solución
| \(\dfrac{210}{385}\) | |
| Utilice árboles de factores para factorizar el numerador y el denominador. | 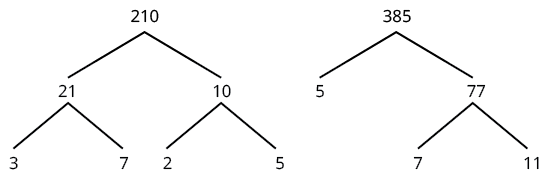 |
| Reescribir el numerador y denominador como producto de los primos. | \(\dfrac{210}{385} = \dfrac{2 \cdot 3 \cdot 5 \cdot 7}{5 \cdot 7 \cdot 11}\) |
| Eliminar los factores comunes. | \(\dfrac{2 \cdot 3 \cdot \cancel{\textcolor{blue}{5}} \cdot \cancel{\textcolor{red}{7}}}{\cancel{\textcolor{blue}{5}} \cdot \cancel{\textcolor{red}{7}} \cdot 11}\) |
| Simplificar. | \(\dfrac{2 \cdot 3}{11}\) |
| Multiplique cualquier factor restante. | \(\dfrac{6}{11}\) |
Simplificar:\(\dfrac{69}{120}\).
- Contestar
-
\(\dfrac{23}{40}\)
Simplificar:\(\dfrac{120}{192}\).
- Contestar
-
\(\dfrac{5}{8}\)
También podemos simplificar fracciones que contienen variables. Si una variable es un factor común en el numerador y denominador, la eliminamos tal como lo hacemos con un factor entero.
Simplificar:\(\dfrac{5xy}{15x}\).
Solución
| \(\dfrac{5xy}{15x}\) | |
| Reescribir numerador y denominador mostrando factores comunes. | \(\dfrac{5 \cdot x \cdot y}{3 \cdot 5 \cdot x}\) |
| Eliminar factores comunes. | \(\dfrac{\cancel{5} \cdot \cancel{x} \cdot y}{3 \cdot \cancel{5} \cdot \cancel{x}}\) |
| Simplificar. | \(\dfrac{y}{3}\) |
Simplificar:\(\dfrac{7x}{7y}\).
- Contestar
-
\(\dfrac{x}{y}\)
Simplificar:\(\dfrac{9a}{9b}\).
- Contestar
-
\(\dfrac{a}{b}\)
Multiplicar fracciones
Un modelo puede ayudarte a entender la multiplicación de fracciones. Utilizaremos baldosas de fracción para modelar\(\dfrac{1}{2} \cdot \dfrac{3}{4}\). Multiplicar\(\dfrac{1}{2}\) y\(\dfrac{3}{4}\), pensar\(\dfrac{1}{2}\) en\(\dfrac{3}{4}\).
Comience con baldosas de fracción por tres cuartos. Para encontrar la mitad de las tres cuartas partes, necesitamos dividirlas en dos grupos iguales. Como no podemos dividir las tres\(\dfrac{1}{4}\) baldosas de manera uniforme en dos partes, las cambiamos por baldosas más pequeñas.
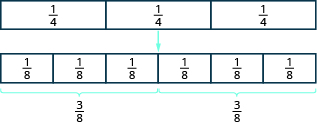
Figura\(\PageIndex{1}\)
Vemos\(\dfrac{6}{8}\) es equivalente a\(\dfrac{3}{4}\). Tomando la mitad de las seis\(\dfrac{1}{8}\) fichas nos da tres\(\dfrac{1}{8}\) fichas, que es\(\dfrac{3}{8}\). Por lo tanto,
\[\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{3}{8} \nonumber \]
Utilice un diagrama para modelar\(\dfrac{1}{2} \cdot \dfrac{3}{4}\).
Solución
Primer matiz en\(\dfrac{3}{4}\) el rectángulo.

Vamos a tomar\(\dfrac{1}{2}\) de esto\(\dfrac{3}{4}\), por lo que fuertemente sombra\(\dfrac{1}{2}\) de la región sombreada.
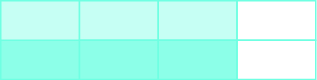
Observe que 3 de las 8 piezas están muy sombreadas. Esto significa que\(\dfrac{3}{8}\) del rectángulo está muy sombreado. Por lo tanto,\(\dfrac{1}{2}\) de\(\dfrac{3}{4}\) es\(\dfrac{3}{4}\), o\(\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{3}{8}\).
Utilice un diagrama para modelar:\(\dfrac{1}{2} \cdot \dfrac{3}{5}\).
- Contestar
-
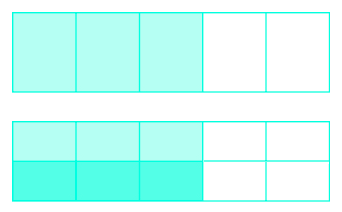
\(\dfrac{3}{10}\)
Utilice un diagrama para modelar:\(\dfrac{1}{2} \cdot \dfrac{5}{6}\).
- Contestar
-
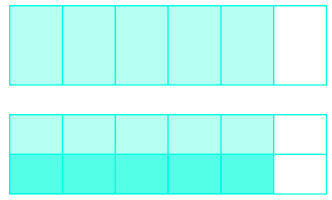
\(\dfrac{5}{12}\)
Mira el resultado que obtuvimos del modelo en Ejemplo\(\PageIndex{6}\). Encontramos eso\(\dfrac{1}{2} \cdot \dfrac{3}{4} = \dfrac{3}{8}\). ¿Se nota que podríamos haber obtenido la misma respuesta multiplicando los numeradores y multiplicando los denominadores?
| \(\dfrac{1}{2} \cdot \dfrac{3}{4}\) | |
| Multiplicar los numeradores y multiplicar los denominadores. | \(\dfrac{1}{2} \cdot \dfrac{3}{4}\) |
| Simplificar. | \(\dfrac{3}{8}\) |
Esto lleva a la definición de multiplicación de fracciones. Para multiplicar fracciones, multiplicamos los numeradores y multiplicamos los denominadores. Después escribimos la fracción en forma simplificada.
Si\(a, b, c,\) y\(d\) son los números donde\(b ≠ 0\) y\(d ≠ 0\), entonces
\[\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\]
Multiplicar, y escribir la respuesta en forma simplificada:\(\dfrac{3}{4} \cdot \dfrac{1}{5}\).
Solución
| \(\dfrac{3}{4} \cdot \dfrac{1}{5}\) | |
| Multiplicar los numeradores y multiplicar los denominadores. | \(\dfrac{3 \cdot 1}{4 \cdot 5}\) |
| Simplificar. | \(\dfrac{3}{20}\) |
No hay factores comunes, por lo que la fracción se simplifica.
Multiplicar, y escribir la respuesta en forma simplificada:\(\dfrac{1}{3} \cdot \dfrac{2}{5}\).
- Contestar
-
\(\dfrac{2}{15}\)
Multiplicar, y escribir la respuesta en forma simplificada:\(\dfrac{3}{5} \cdot \dfrac{7}{8}\).
- Contestar
-
\(\dfrac{21}{40}\)
Al multiplicar fracciones, siguen aplicándose las propiedades de los números positivos y negativos. Es una buena idea determinar el signo del producto como primer paso. En Ejemplo\(\PageIndex{8}\) vamos a multiplicar dos negativos, por lo que el producto será positivo.
Multiplicar, y escribir la respuesta en forma simplificada:\(- \dfrac{5}{8} \left(- \dfrac{2}{3}\right)\).
Solución
| \(- \dfrac{5}{8} \left(- \dfrac{2}{3}\right)\) | |
| Los signos son los mismos, por lo que el producto es positivo. Multiplicar los numeradores, multiplicar los denominadores. | \(\dfrac{5 \cdot 2}{8 \cdot 3}\) |
| Simplificar. | \(\dfrac{10}{24}\) |
| Busque factores comunes en el numerador y denominador. Reescritura mostrando factores comunes. | \(\dfrac{5 \cdot \cancel{\textcolor{red}{2}}}{12 \cdot \cancel{\textcolor{red}{2}}}\) |
| Eliminar factores comunes. | \(\dfrac{5}{12}\) |
Otra forma de encontrar este producto implica eliminar factores comunes antes.
| \(- \dfrac{5}{8} \left(- \dfrac{2}{3}\right)\) | |
| Determinar el signo del producto. Multiplicar. | \(\dfrac{5 \cdot 2}{8 \cdot 3}\) |
| Mostrar factores comunes y luego eliminarlos. | \(\dfrac{5 \cdot \cancel{\textcolor{red}{2}}}{12 \cdot \cancel{\textcolor{red}{2}}}\) |
| Multiplicar los factores restantes. | \(\dfrac{5}{12}\) |
Obtenemos el mismo resultado.
Multiplicar, y escribir la respuesta en forma simplificada:\(- \dfrac{4}{7} \left(- \dfrac{5}{8}\right)\).
- Contestar
-
\(\dfrac{5}{14}\)
Multiplicar, y escribir la respuesta en forma simplificada:\(- \dfrac{7}{12} \left(- \dfrac{8}{9}\right)\).
- Contestar
-
\(\dfrac{14}{27}\)
Multiplicar, y escribir la respuesta en forma simplificada:\(− \dfrac{14}{15} \cdot \dfrac{20}{21}\).
Solución
| \(- \dfrac{14}{15} \cdot \dfrac{20}{21}\) | |
| Determinar el signo del producto; multiplicar. | \(- \dfrac{14}{15} \cdot \dfrac{20}{21}\) |
| ¿Hay algún factor común en el numerador y en el denominador? Sabemos que 7 es un factor de 14 y 21, y 5 es un factor de 20 y 15. | |
| Reescritura mostrando factores comunes. | \(- \dfrac{2 \cdot \cancel{\textcolor{red}{7}} \cdot 4 \cdot \cancel{\textcolor{red}{5}}}{3 \cdot \cancel{\textcolor{red}{5}} \cdot 3 \cdot \cancel{\textcolor{red}{7}}}\) |
| Eliminar los factores comunes. | \(- \dfrac{2 \cdot 4}{3 \cdot 3}\) |
| Multiplicar los factores restantes. | \(- \dfrac{8}{9}\) |
Multiplicar, y escribir la respuesta en forma simplificada:\(− \dfrac{10}{28} \cdot \dfrac{8}{15}\).
- Contestar
-
\(-\dfrac{4}{21}\)
Multiplicar, y escribir la respuesta en forma simplificada:\(− \dfrac{9}{20} \cdot \dfrac{5}{12}\).
- Contestar
-
\(-\dfrac{3}{16}\)
Al multiplicar una fracción por un entero, puede ser útil escribir el entero como una fracción. Cualquier entero, a, puede escribirse como\(\dfrac{a}{1}\). Entonces\(3 = \dfrac{3}{1}\), por ejemplo.
Multiplica y escribe la respuesta en forma simplificada:
- \(\dfrac{1}{7} \cdot 56\)
- \(\dfrac{12}{5} (−20x)\)
Solución
| \(\dfrac{1}{7} \cdot 56\) | |
| Escribe 56 como una fracción. | \(\dfrac{1}{7} \cdot \dfrac{56}{1}\) |
| Determinar el signo del producto; multiplicar. | \(\dfrac{56}{7}\) |
| Simplificar. | \(8\) |
| \(\dfrac{12}{5} (-20x)\) | |
| Escribe −20x como una fracción. | \(\dfrac{12}{5} \left(\dfrac{-20x}{1}\right)\) |
| Determinar el signo del producto; multiplicar. | \(- \dfrac{12 \cdot 20 \cdot x}{5 \cdot 1}\) |
| Mostrar factores comunes y luego eliminarlos. | \(- \dfrac{12 \cdot \textcolor{red}{4 \cdot \cancel{5} x}}{\cancel{5} \cdot 1}\) |
| Multiplicar los factores restantes; simplificar. | \(-48x\) |
Multiplica y escribe la respuesta en forma simplificada:
- \(\dfrac{1}{8} • 72\)
- \(\dfrac{11}{3} (−9a)\)
- Contestar a
-
\(9\)
- Respuesta b
-
\(-33a\)
Multiplica y escribe la respuesta en forma simplificada:
- \(\dfrac{3}{8} • 64\)
- \(16x • \dfrac{11}{12}\)
- Contestar a
-
\(24\)
- Respuesta b
-
\(\dfrac{44x}{3}\)


