4.4: Multiplicar y dividir fracciones (Parte 2)
- Page ID
- 114243
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Buscar Reciprocales
Las fracciones\(\dfrac{2}{3}\) y\(\dfrac{3}{2}\) están relacionadas entre sí de una manera especial. Así son\(− \dfrac{10}{7}\) y\(− \dfrac{7}{10}\). ¿Ves cómo? Además de parecer versiones al revés unas de otras, si tuviéramos que multiplicar estos pares de fracciones, el producto sería 1.
\[\dfrac{2}{3} \cdot \dfrac{3}{2} = 1 \quad and \quad - \dfrac{10}{7} \left(- \dfrac{7}{10}\right) = 1 \tag{4.2.53} \nonumber \]
Tales pares de números se llaman recíprocos.
El recíproco de la fracción\(\dfrac{a}{b}\) es\(\dfrac{b}{a}\), dónde\(a ≠ 0\) y\(b ≠ 0\).
Un número y su recíproco tienen un producto de\(1\).
\[\dfrac{a}{b} \cdot \dfrac{b}{a} = 1 \tag{4.2.54}\]
Para encontrar el recíproco de una fracción, invertimos la fracción. Esto significa que colocamos el numerador en el denominador y el denominador en el numerador.
Para obtener un resultado positivo al multiplicar dos números, los números deben tener el mismo signo. Por lo que los recíprocos deben tener el mismo signo.

Para encontrar el recíproco, mantener el mismo signo e invertir la fracción. El número cero no tiene un recíproco. ¿Por qué? Un número y su recíproco se multiplican a\(1\). ¿Hay algún número\(r\) así\(0 • r = 1\)? No. Entonces, el número\(0\) no tiene un recíproco.
Encuentra el recíproco de cada número. Después comprobar que el producto de cada número y su recíproco es\(1\).
- \(\dfrac{4}{9}\)
- \(− \dfrac{1}{6}\)
- \(− \dfrac{14}{5}\)
- \(7\)
Solución
Para encontrar los recíprocos, mantenemos el signo e invertimos las fracciones.
| Encuentra el recíproco de\(\dfrac{4}{9}\). | El recíproco de\(\dfrac{4}{9}\) es\(\dfrac{9}{4}\). |
Comprobar:
| Multiplicar el número y su recíproco. | \(\dfrac{4}{9} \cdot \dfrac{9}{4}\) |
| Multiplicar numeradores y denominadores. | \(\dfrac{36}{36} \) |
| Simplificar. | \(1 \; \checkmark \) |
| Encuentra el recíproco de\(- \dfrac{1}{6}\). | El recíproco de\(- \dfrac{1}{6}\) es\(\dfrac{6}{1}\). |
| Simplificar. | \(-6 \) |
| Cheque. | \(- \dfrac{1}{6} \cdot (-6) = 1 \; \checkmark \) |
| Encuentra el recíproco de\(- \dfrac{14}{5}\). | \(- \dfrac{5}{14} \) |
| Cheque. | \(- \dfrac{14}{5} \cdot \left(- \dfrac{5}{14}\right) = \dfrac{70}{70} = 1 \; \checkmark \) |
| Encuentra el recíproco de 7. | |
| Escribe 7 como una fracción. | \(\dfrac{7}{1}\) |
| Escribir el recíproco de\(\dfrac{7}{1}\). | \(\dfrac{1}{7} \) |
| Cheque. | \(7 \cdot \left(\dfrac{1}{7}\right) = 1 \; \checkmark \) |
Encuentra el recíproco:
- \(\dfrac{5}{7}\)
- \(− \dfrac{1}{8}\)
- \(− \dfrac{11}{4}\)
- \(14\)
- Contestar a
-
\(\dfrac{7}{5}\)
- Respuesta b
-
\(-8\)
- Respuesta c
-
\(-\dfrac{4}{11}\)
- Respuesta d
-
\(\dfrac{1}{14}\)
Encuentra el recíproco:
- \(\dfrac{3}{7}\)
- \(− \dfrac{1}{12}\)
- \(− \dfrac{14}{9}\)
- \(21\)
- Contestar a
-
\(\dfrac{7}{3}\)
- Respuesta b
-
\(-12\)
- Respuesta c
-
\(-\dfrac{9}{14}\)
- Respuesta d
-
\(\dfrac{1}{21}\)
En un capítulo anterior, trabajamos con opuestos y valores absolutos. Tabla\(\PageIndex{1}\) compara opuestos, valores absolutos y recíprocos.
| Opuesto | Valor Absoluto | recíproco |
|---|---|---|
| tiene signo opuesto | nunca es negativo | tiene el mismo signo, fracción invierte |
Rellene el gráfico para cada fracción en la columna de la izquierda:
| Número | Opuesto | Valor Absoluto | recíproco |
|---|---|---|---|
| \(- \dfrac{3}{8}\) | |||
| \(\dfrac{1}{2}\) | |||
| \(\dfrac{9}{5}\) | |||
| \(-5\) |
Solución
Para encontrar lo contrario, cambie el signo. Para encontrar el valor absoluto, deje los números positivos iguales, pero tome lo contrario de los números negativos. Para encontrar lo recíproco, mantenga el signo igual e invierta la fracción.
| Número | Opuesto | Valor Absoluto | recíproco |
|---|---|---|---|
| \(- \dfrac{3}{8}\) | \(\dfrac{3}{8}\) | \(\dfrac{3}{8}\) | \(- \dfrac{8}{3}\) |
| \(\dfrac{1}{2}\) | \(- \dfrac{1}{2}\) | \(\dfrac{1}{2}\) | \(2\) |
| \(\dfrac{9}{5}\) | \(- \dfrac{9}{5}\) | \(\dfrac{9}{5}\) | \(\dfrac{5}{9}\) |
| \(-5\) | \(5\) | \(5\) | \(- \dfrac{1}{5}\) |
Rellena la tabla para cada número dado:
| Número | Opuesto | Valor Absoluto | recíproco |
|---|---|---|---|
| \(- \dfrac{5}{8}\) | |||
| \(\dfrac{1}{4}\) | |||
| \(\dfrac{8}{3}\) | |||
| \(-8\) |
- Contestar
-
Número Opuesto Valor Absoluto recíproco \(-\dfrac{5}{8}\) \(\dfrac{5}{8}\) \(\dfrac{5}{8}\) \(-\dfrac{8}{5}\) \(\dfrac{1}{4}\) \(-\dfrac{1}{4}\) \(\dfrac{1}{4}\) \(4\) \(\dfrac{8}{3}\) \(-\dfrac{8}{3}\) \(\dfrac{8}{3}\) \(\dfrac{3}{8}\) \(-8\) \(8\) \(8\) \(-\dfrac{1}{8}\)
Rellena la tabla para cada número dado:
| Número | Opuesto | Valor Absoluto | recíproco |
|---|---|---|---|
| \(- \dfrac{4}{7}\) | |||
| \(\dfrac{1}{8}\) | |||
| \(\dfrac{9}{4}\) | |||
| \(-1\) |
- Contestar
-
Número Opuesto Valor Absoluto recíproco \(-\dfrac{4}{7}\) \(\dfrac{4}{7}\) \(\dfrac{4}{7}\) \(- \dfrac{7}{4}\) \(\dfrac{1}{8}\) \(-\dfrac{1}{8}\) \(\dfrac{1}{8}\) \(8\) \(\dfrac{9}{4}\) \(-\dfrac{9}{4}\) \(\dfrac{9}{4}\) \(\dfrac{4}{9}\) \(-1\) \(1\) \(1\) \(-\dfrac{1}{1}\)
Dividir fracciones
¿Por qué es\(12 ÷ 3 = 4\)? Anteriormente modelamos esto con contadores. ¿Cuántos grupos de\(3\) contadores se pueden hacer a partir de un grupo de\(12\) contadores?

Figura\(\PageIndex{2}\)
Hay\(4\) grupos de\(3\) mostradores. En otras palabras, hay cuatro\(3\) s en\(12\). Entonces,\(12 ÷ 3 = 4\).
¿Qué pasa con dividir fracciones? Supongamos que queremos encontrar el cociente:\(\dfrac{1}{2} \div \dfrac{1}{6}\). Tenemos que averiguar en cuántos\(\dfrac{1}{6}\) s hay\(\dfrac{1}{2}\). Podemos usar mosaicos de fracción para modelar esta división. Comenzamos alineando las baldosas de media y sexta fracción como se muestra en la Figura\(\PageIndex{3}\). Observe, hay tres\(\dfrac{1}{6}\) mosaicos en\(\dfrac{1}{2}\), entonces\(\dfrac{1}{2} \div \dfrac{1}{6} = 3\).

Figura\(\PageIndex{3}\)
Modelo:\(\dfrac{1}{4} \div \dfrac{1}{8}\).
Solución
Queremos determinar cuántos\(\dfrac{1}{8}\) s hay en\(\dfrac{1}{4}\). Comience con una\(\dfrac{1}{4}\) baldosa. Alinee\(\dfrac{1}{8}\) las baldosas debajo de la\(\dfrac{1}{4}\) loseta.
Modelo:\(\dfrac{1}{3} \div \dfrac{1}{6}\).
- Contestar
-

Modelo:\(\dfrac{1}{2} \div \dfrac{1}{4}\).
- Contestar
-

Modelo:\(2 ÷ \dfrac{1}{4}\).
Solución
Estamos tratando de determinar cuántos\(\dfrac{1}{4}\) s hay en\(2\). Podemos modelar esto como se muestra.

Porque hay ocho\(\dfrac{1}{4}\) s en\(2\),\(2 ÷ \dfrac{1}{4} = 8\).
Modelo:\(2 ÷ \dfrac{1}{3}\)
- Contestar
-

Modelo:\(3 ÷ \dfrac{1}{2}\)
- Contestar
-

Usemos el dinero para modelar\(2 ÷ \dfrac{1}{4}\) de otra manera. A menudo leemos\(\dfrac{1}{4}\) como un 'trimestre', y sabemos que un trimestre es un cuarto de dólar como se muestra en la Figura\(\PageIndex{4}\). Entonces podemos pensar en\(2 ÷ \dfrac{1}{4}\) como, “¿Cuántos trimestres hay en dos dólares?” Un dólar son\(4\) trimestres, por lo que los\(2\) dólares serían\(8\) trimestres. Entonces otra vez,\(2 ÷ \dfrac{1}{4} = 8\).

Figura:La moneda\(\PageIndex{4}\) estadounidense llamada cuarto vale un cuarto de dólar.
Usando baldosas de fracción, lo demostramos\(\dfrac{1}{2} \div \dfrac{1}{6} = 3\). Observe que\(\dfrac{1}{2} \cdot \dfrac{6}{1} = 3\) también. ¿Cómo están\(\dfrac{1}{6}\) y\(\dfrac{6}{1}\) relacionados? Son recíprocos. Esto nos lleva al procedimiento para la división de fracciones.
Si\(a, b, c,\) y\(d\) son números donde\(b ≠ 0\),\(c ≠ 0\), y\(d ≠ 0\), entonces
\[\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c} \]
Para dividir fracciones, multiplique la primera fracción por el recíproco de la segunda.
Tenemos que decirlo\(b ≠ 0\),\(c ≠ 0\) y\(d ≠ 0\) para estar seguros no dividimos por cero.
Divide, y escribe la respuesta en forma simplificada:\ (\ dfrac {2} {5}\ div\ left (-\ dfrac {3} {7}\ right).
Solución
| Multiplicar la primera fracción por el recíproco de la segunda. | \(\dfrac{2}{5} \left(- \dfrac{7}{3}\right) \) |
| Multiplicar. El producto es negativo. | \(- \dfrac{14}{15}\) |
Dividir, y escribir la respuesta en forma simplificada:\(\dfrac{3}{7} \div \left(− \dfrac{2}{3}\right)\).
- Contestar
-
\(-\dfrac{9}{14}\)
Dividir, y escribir la respuesta en forma simplificada:\(\dfrac{2}{3} \div \left(− \dfrac{7}{5}\right)\).
- Contestar
-
\(-\dfrac{10}{21}\)
Dividir, y escribir la respuesta en forma simplificada:\(\dfrac{2}{3} \div \dfrac{n}{5}\).
Solución
| Multiplicar la primera fracción por el recíproco de la segunda. | \(\dfrac{2}{3} \div \dfrac{5}{n} \) |
| Multiplicar. | \(\dfrac{10}{3n}\) |
Dividir, y escribir la respuesta en forma simplificada:\(\dfrac{3}{5} \div \dfrac{p}{7}\).
- Contestar
-
\(\dfrac{21}{5p}\)
Dividir, y escribir la respuesta en forma simplificada:\(\dfrac{5}{8} \div \dfrac{q}{3}\).
- Contestar
-
\(\dfrac{15}{8q}\)
Dividir, y escribir la respuesta en forma simplificada:\(− \dfrac{3}{4} \div \left(− \dfrac{7}{8}\right)\).
Solución
| Multiplicar la primera fracción por el recíproco de la segunda. | \(- \dfrac{3}{4} \cdot \left(- \dfrac{8}{7}\right) \) |
| Multiplicar. Recuerda determinar primero el signo. | \(\dfrac{3 \cdot 8}{4 \cdot 7}\) |
| Reescribir para mostrar factores comunes. | \(\dfrac{3 \cdot \cancel{4} \cdot 2}{\cancel{4} \cdot 7} \) |
| Elimine los factores comunes y simplifique. | \(\dfrac{6}{7} \) |
Dividir, y escribir la respuesta en forma simplificada:\(− \dfrac{2}{3} \div \left(− \dfrac{5}{6}\right)\).
- Contestar
-
\(\dfrac{4}{5}\)
Dividir, y escribir la respuesta en forma simplificada:\(− \dfrac{5}{6} \div \left(− \dfrac{2}{3}\right)\).
- Contestar
-
\(\dfrac{5}{4}\)
Dividir, y escribir la respuesta en forma simplificada:\(\dfrac{7}{18} \div \dfrac{14}{27}\).
Solución
| Multiplicar la primera fracción por el recíproco de la segunda. | \(\dfrac{7}{18} \cdot \dfrac{27}{14} \) |
| Multiplicar. | \(\dfrac{7 \cdot 27}{18 \cdot 14} \) |
| Reescritura mostrando factores comunes. | \(\dfrac{\cancel{\textcolor{red}{7}} \cdot \cancel{\textcolor{red}{9}} \cdot 3}{\cancel{\textcolor{red}{9}} \cdot \cancel{\textcolor{red}{7}} \cdot 2}\) |
| Eliminar factores comunes. | \(\dfrac{3}{2 \cdot 2} \) |
| Simplificar. | \(\dfrac{3}{4} \) |
Dividir, y escribir la respuesta en forma simplificada:\(\dfrac{7}{27} \div \dfrac{35}{36}\).
- Contestar
-
\(\dfrac{4}{15}\)
Dividir, y escribir la respuesta en forma simplificada:\(\dfrac{5}{14} \div \dfrac{15}{28}\).
- Contestar
-
\(\dfrac{2}{3}\)
Acceda a recursos adicionales en línea
Conceptos clave
- Propiedad Fracciones Equivalentes
- Si\(a, b, c\) son los números donde\(b\neq 0, c\neq 0\), entonces\(\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\) y\(\dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\)
- Simplifica una fracción.
- Reescribir el numerador y denominador para mostrar los factores comunes. Si es necesario, factive el numerador y el denominador en números primos.
- Simplifique, usando la propiedad de fracciones equivalentes, eliminando factores comunes.
- Multiplique cualquier factor restante.
- Multiplicación de Fracciones
- Si\(a, b, c,\) y
- Reciproca
- Un número y su recíproco tienen un producto de 1. \(\frac{a}{b} \cdot \frac{b}{a} = 1\)
-
Opuesto Valor Absoluto recíproco tiene signo opuesto nunca es negativo tiene el mismo signo, fracción invierte
- División de Fracciones
- Si\(a, b, c,\) y\(d\) son números donde\(b\neq 0\),\(c\neq 0\), y\(d\neq 0\), entonces\(\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b}\cdot \dfrac{d}{c}\)
- Para dividir fracciones, multiplique la primera fracción por el recíproco de la segunda.
Glosario
- recíproco
-
El recíproco de la fracción\(\dfrac{a}{b}\) es\(\dfrac{b}{a}\) dónde\(a\neq 0\) y\(b\neq 0\).
- fracción simplificada
-
Una fracción se considera simplificada si no hay factores comunes en el numerador y denominador.
La práctica hace la perfección
Simplificar fracciones
En los siguientes ejercicios, simplifique cada fracción. No convierta ninguna fracción impropia en números mixtos.
- \(\dfrac{7}{21}\)
- \(\dfrac{8}{24}\)
- \(\dfrac{15}{20}\)
- \(\dfrac{12}{18}\)
- \(- \dfrac{40}{88}\)
- \(- \dfrac{63}{99}\)
- \(- \dfrac{108}{63}\)
- \(- \dfrac{104}{48}\)
- \(\dfrac{120}{252}\)
- \(\dfrac{182}{294}\)
- \(- \dfrac{168}{192}\)
- \(- \dfrac{140}{224}\)
- \(\dfrac{11x}{11y}\)
- \(\dfrac{15a}{15b}\)
- \(− \dfrac{3x}{12y}\)
- \(− \dfrac{4x}{32y}\)
- \(\dfrac{14x^{2}}{21y}\)
- \(\dfrac{24a}{32b^{2}}\)
Multiplicar fracciones
En los siguientes ejercicios, utilice un diagrama para modelar.
- \(\dfrac{1}{2} \cdot \dfrac{2}{3}\)
- \(\dfrac{1}{2} \cdot \dfrac{5}{8}\)
- \(\dfrac{1}{3} \cdot \dfrac{5}{6}\)
- \(\dfrac{1}{3} \cdot \dfrac{2}{5}\)
En los siguientes ejercicios, multiplique y escriba la respuesta de forma simplificada.
- \(\dfrac{2}{5} \cdot \dfrac{1}{3}\)
- \(\dfrac{1}{2} \cdot \dfrac{3}{8}\)
- \(\dfrac{3}{4} \cdot \dfrac{9}{10}\)
- \(\dfrac{4}{5} \cdot \dfrac{2}{7}\)
- \(− \dfrac{2}{3} \left(− \dfrac{3}{8}\right)\)
- \(− \dfrac{3}{4} \left(− \dfrac{4}{9}\right)\)
- \(- \dfrac{5}{9} \cdot \dfrac{3}{10}\)
- \(- \dfrac{3}{8} \cdot \dfrac{4}{15}\)
- \(− \dfrac{7}{12} \left(− \dfrac{8}{21}\right)\)
- \(\dfrac{5}{12} \left(− \dfrac{8}{15}\right)\)
- \(\left(− \dfrac{14}{15}\right) \left(\dfrac{9}{20}\right)\)
- \(\left(− \dfrac{9}{10}\right) \left(\dfrac{25}{33}\right)\)
- \(\left(− \dfrac{63}{84}\right) \left(- \dfrac{44}{90}\right)\)
- \(\left(− \dfrac{33}{60}\right) \left(- \dfrac{40}{88}\right)\)
- \(4 \cdot \dfrac{5}{11}\)
- \(5 \cdot \dfrac{8}{3}\)
- \(\dfrac{3}{7} \cdot 21n\)
- \(\dfrac{5}{6} \cdot 30m\)
- \(−28p \left(− \dfrac{1}{4}\right)\)
- \(−51q \left(− \dfrac{1}{3}\right)\)
- \(−8 \left(\dfrac{17}{4}\right)\)
- \(\dfrac{14}{5} (−15)\)
- \(−1 \left(− \dfrac{3}{8}\right)\)
- \((−1) \left(- \dfrac{6}{7}\right)\)
- \(\left(\dfrac{2}{3}\right)^{3}\)
- \(\left(\dfrac{4}{5}\right)^{2}\)
- \(\left(\dfrac{6}{5}\right)^{4}\)
- \(\left(\dfrac{4}{7}\right)^{4}\)
Encuentra Reciprocales En los siguientes ejercicios, encuentra el recíproco.
- \(\dfrac{3}{4}\)
- \(\dfrac{2}{3}\)
- \(− \dfrac{5}{17}\)
- \(− \dfrac{6}{19}\)
- \(\dfrac{11}{8}\)
- −13
- −19
- −1
- 1
- Rellene la tabla.
Opuesto Valor Absoluto recíproco \(- \dfrac{7}{11}\) \(\dfrac{4}{5}\) \(\dfrac{10}{7}\) \(-8\) - Rellene la tabla.
Opuesto Valor Absoluto recíproco \(- \dfrac{3}{13}\) \(\dfrac{9}{14}\) \(\dfrac{15}{7}\) \(-9\)
Dividir fracciones
En los siguientes ejercicios, modele cada división de fracciones.
- \(\dfrac{1}{2} \div \dfrac{1}{4}\)
- \(\dfrac{1}{2} \div \dfrac{1}{8}\)
- \(2 \div \dfrac{1}{5}\)
- \(3 \div \dfrac{1}{4}\)
En los siguientes ejercicios, divida y escriba la respuesta de forma simplificada.
- \(\dfrac{1}{2} \div \dfrac{1}{4}\)
- \(\dfrac{1}{2} \div \dfrac{1}{8}\)
- \(\dfrac{3}{4} \div \dfrac{2}{3}\)
- \(\dfrac{4}{5} \div \dfrac{3}{4}\)
- \(- \dfrac{4}{5} \div \dfrac{4}{7}\)
- \(- \dfrac{3}{4} \div \dfrac{3}{5}\)
- \(− \dfrac{7}{9} \div \left(- \dfrac{7}{9}\right)\)
- \(− \dfrac{5}{6} \div \left(- \dfrac{5}{6}\right)\)
- \(\dfrac{3}{4} \div \dfrac{x}{11}\)
- \(\dfrac{2}{5} \div \dfrac{y}{9}\)
- \(\dfrac{5}{8} \div \dfrac{a}{10}\)
- \(\dfrac{5}{6} \div \dfrac{c}{15}\)
- \(\dfrac{5}{18} \div \left(- \dfrac{15}{24}\right)\)
- \(\dfrac{7}{18} \div \left(- \dfrac{14}{27}\right)\)
- \(\dfrac{7p}{12} \div \dfrac{21p}{8}\)
- \(\dfrac{5q}{12} \div \dfrac{15q}{8}\)
- \(\dfrac{8u}{15} \div \dfrac{12v}{25}\)
- \(\dfrac{12r}{25} \div \dfrac{18s}{35}\)
- \(-5 \div \dfrac{1}{2}\)
- \(-3 \div \dfrac{1}{4}\)
- \(\dfrac{3}{4} \div (-12)\)
- \(\dfrac{2}{5} \div (-10)\)
- \(−18 \div \left(− \dfrac{9}{2}\right)\)
- \(−15 \div \left(− \dfrac{5}{3}\right)\)
- \(\dfrac{1}{2} \div \left(- \dfrac{3}{4}\right) \div \dfrac{7}{8}\)
- \(\dfrac{11}{2} \div \dfrac{7}{8} \cdot \dfrac{2}{11}\)
Matemáticas cotidianas
- Hornear Una receta de galletas con chispas de chocolate requiere 3 4 tazas de azúcar moreno. Imelda quiere duplicar la receta.
- ¿Cuánto azúcar moreno necesitará Imelda? Muestra tu cálculo. Escribe tu resultado como una fracción impropia y como un número mixto.
- Los vasos medidores generalmente vienen en juegos de\(\dfrac{1}{8}, \dfrac{1}{4}, \dfrac{1}{3}, \dfrac{1}{2}\), y 1 taza. Dibuja un diagrama para mostrar dos formas diferentes en las que Imelda podría medir el azúcar moreno necesario para duplicar la receta.
- Hornear Nina está haciendo 4 sartenes de dulce de azúcar para servir después de un recital musical. Por cada sartén, necesita 2 3 tazas de leche condensada.
- ¿Cuánta leche condensada necesitará Nina? Muestra tu cálculo. Escribe tu resultado como una fracción impropia y como un número mixto.
- Los vasos medidores generalmente vienen en juegos de\(\dfrac{1}{8}, \dfrac{1}{4}, \dfrac{1}{3}, \dfrac{1}{2}\), y 1 taza. Dibuja un diagrama para mostrar dos formas diferentes en las que Nina podría medir la leche condensada que necesita.
- Porciones Don compró un paquete a granel de dulces que pesa 5 libras. Quiere vender los dulces en bolsitas que contienen\(\dfrac{1}{4}\) libra. ¿Cuántas bolsitas de dulces puede llenar del paquete a granel?
- Porciones Kristen tiene\(\dfrac{3}{4}\) yardas de cinta. Ella quiere cortarlo en partes iguales para hacer cintas de pelo para las 6 muñecas de su hija. ¿Cuánto tiempo durará la cinta para el pelo de cada muñeca?
Ejercicios de escritura
- Explica cómo encuentras el recíproco de una fracción.
- Explica cómo encuentras el recíproco de una fracción negativa.
- Rafael quería pedir media pizza mediana en un restaurante. El mesero le dijo que una pizza mediana se podía cortar en 6 u 8 rebanadas. ¿Preferiría 3 de 6 rebanadas o 4 de 8 rebanadas? Rafael respondió que como no tenía mucha hambre, preferiría 3 de cada 6 rebanadas. Explique qué hay de malo en el razonamiento de Rafael.
- Dar un ejemplo de la vida cotidiana que demuestre cómo\(\dfrac{1}{2} \cdot \dfrac{2}{3}\) es\(\dfrac{1}{3}\).
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
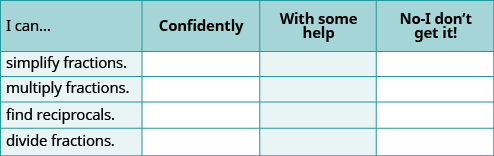
(b) Después de revisar esta lista de verificación, ¿qué hará para confiar en todos los objetivos?


