5.1.1: Interpretación de números negativos

Última actualización
Guardar como PDF

Page ID: 119271

Illustrative Mathematics
OpenUp Resources

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lección

Repasemos lo que sabemos sobre los números firmados.

Ejercicio$\PageIndex{1}$: Using the Thermometer

Aquí hay un termómetro meteorológico. Tres de los números se han dejado fuera.

Figura$\PageIndex{1}$: Termómetro vertical medido en grados Celsius. Hay 9 marcas de graduación espaciadas uniformemente y comenzando desde la parte inferior del termómetro, el negativo 10 está en la primera marca, cero en la tercera, 5 en la cuarta, 15 en la sexta, 20 en la séptima y 30 en la novena. Cada una de las marcas de verificación segunda, quinta y octava está etiquetada con una casilla. El termómetro se sombrea comenzando desde la parte inferior del termómetro hasta la mitad entre la segunda y la tercera marca de graduación.

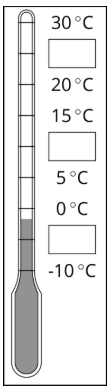
¿Qué números van en las cajas?
¿Qué temperatura muestra el termómetro?

Ejercicio$\PageIndex{2}$: Fractions of a Degree

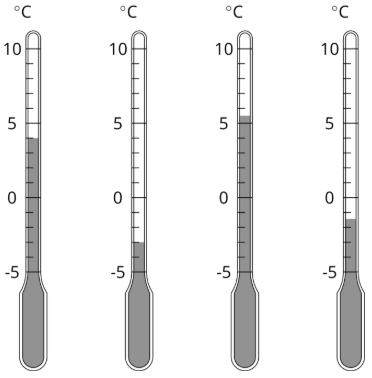
¿Qué temperatura se muestra en cada termómetro?
¿Qué termómetro muestra la temperatura más alta?
¿Qué termómetro muestra la temperatura más baja?
Supongamos que la temperatura exterior es$-4^{\circ}\text{C}$. ¿Eso es más frío o más cálido que la temperatura más fría que se muestra? ¿Cómo lo sabes?

Figura$\PageIndex{2}$: Cuatro termómetros verticales medidos en grados Celsius. Hay 16 marcas de graduación espaciadas uniformemente y comenzando desde la parte inferior del termómetro, el negativo 5 está en la primera marca, cero en la sexta, 5 en la undécima y 10 en la decimosexta. El primer termómetro está sombreado comenzando desde la parte inferior del termómetro hasta la décima marca de verificación. El segundo termómetro está sombreado comenzando desde la parte inferior del termómetro hasta la tercera marca de verificación. El tercer termómetro está sombreado comenzando desde la parte inferior del termómetro hasta entre la undécima y duodécima marca de verificación. El cuarto termómetro se sombrea comenzando desde la parte inferior del termómetro hasta entre la cuarta y quinta marca de verificación.

Ejercicio$\PageIndex{3}$: Seagulls Soar, SHarks Swim

Aquí hay una foto de algunos animales marinos. La recta numérica de la izquierda muestra la posición vertical de cada animal por encima o por debajo del nivel del mar, en metros.

Figura$\PageIndex{3}$: Una gráfica. El eje vertical está etiquetado como posición vertical, en metros. 5 marcas de verificación. Escala de negativo 15 a 15, por 5s. El eje horizontal no tiene etiqueta ni escala. Gaviota está a las 10. Dolphin está a las 3. Pingüino está a 0. El tiburón está en negativo 3. El pez está en negativo 7. El pulpo está en negativo 10.

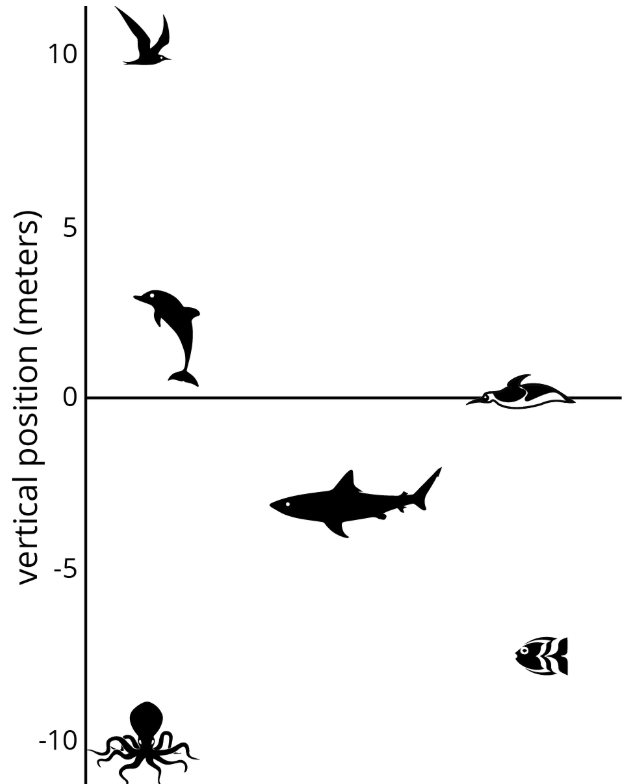
¿Qué tan alto o bajo el nivel del mar está cada animal? Mida a su nivel de ojos.
Un rayo mobula se encuentra a 3 metros sobre la superficie del océano. ¿Cómo se compara su posición vertical con la altura o profundidad de:
El delfín saltador?
¿La gaviota voladora?
¿El pulpo?
Un albatros se encuentra a 5 metros sobre la superficie del océano. ¿Cómo se compara su posición vertical con la altura o profundidad de:
El delfín saltador?
¿La gaviota voladora?
¿El pulpo?
Un pez payaso se encuentra a 2 metros por debajo de la superficie del océano. ¿Cómo se compara su posición vertical con la altura o profundidad de:
El delfín saltador?
¿La gaviota voladora?
¿El pulpo?
La distancia vertical de un nuevo delfín del delfín en la imagen es de 3 metros. ¿Cuál es su distancia de la superficie del océano?

¿Estás listo para más?

El polo norte se encuentra en medio del océano. Una persona a nivel del mar en el polo norte estaría a 3,949 millas del centro de la Tierra. El fondo marino por debajo del polo norte se encuentra a una altitud de aproximadamente -2.7 millas. La elevación del polo sur es de aproximadamente 1.7 millas. ¿A qué distancia está una persona parada en el polo sur de un submarino en el fondo marino debajo del polo norte?

Ejercicio$\PageIndex{4}$: Card Sort: Rational Numbers

Tu profesor le dará a tu grupo un juego de tarjetas. Ordene las tarjetas de menor a mayor.
Haz una pausa aquí para que tu profesor pueda revisar tu trabajo. Entonces, tu profesor te dará un segundo juego de tarjetas.
Agrega el nuevo juego de cartas al primer set para que todas las cartas se ordenen de menor a mayor.

Resumen

Podemos usar números positivos y negativos para representar la temperatura y la elevación.

Cuando los números representan temperaturas, los números positivos indican temperaturas que son más cálidas que cero y los números negativos indican temperaturas que son más frías que cero. Este termómetro muestra una temperatura de -1 grado Celsius, que escribimos$-1^{\circ}\text{C}$.

Figura$\PageIndex{4}$: Un termómetro posicionado horizontalmente y con la parte inferior del termómetro a la izquierda, está etiquetado grados Celsius. Hay 4 marcas grandes espaciadas uniformemente. Comenzando por la izquierda, las marcas grandes se etiquetan como negativas 5, 0, 5 y 10. Entre cada marca grande, hay 4 marcas pequeñas espaciadas uniformemente. El termómetro está sombreado, comenzando por la izquierda, hasta negativo 1.

Cuando los números representan elevaciones, los números positivos indican posiciones sobre el nivel del mar y los negativos indican posiciones por debajo del nivel del mar.

Podemos ver el orden de los números firmados en una línea numérica.

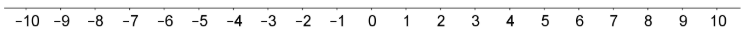
Un número es siempre menor que los números a su derecha. Entonces$-7<-3$.

Usamos el valor absoluto para describir qué tan lejos está un número de 0. Los números 15 y -15 son ambos 15 unidades de 0, así$|15|=15$ y$|-15|=15$. Llamamos 15 y -15 opuestos. Están en lados opuestos de 0 en la recta numérica, pero a la misma distancia de 0.

Entradas en el glosario

Definición: Valor Absoluto

El valor absoluto de un número es su distancia de 0 en la recta numérica.

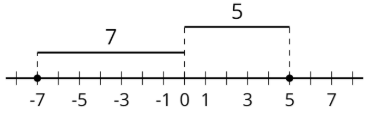
El valor absoluto de -7 es 7, porque está a 7 unidades de distancia de 0. El valor absoluto de 5 es 5, porque está a 5 unidades de distancia de 0.

Definición: Número negativo

Un número negativo es un número que es menor que cero. En una recta numérica horizontal, los números negativos generalmente se muestran a la izquierda de 0.

Definición: Número positivo

Un número positivo es un número que es mayor que cero. En una recta numérica horizontal, los números positivos generalmente se muestran a la derecha de 0.

Practica

Ejercicio$\PageIndex{5}$

Fue$-5^{\circ}\text{C}$ en Copenhague y$-12^{\circ}\text{C}$ en Oslo. ¿Qué ciudad estaba más fría?

Ejercicio$\PageIndex{6}$

Un pez se encuentra a 12 metros por debajo de la superficie del océano. ¿Cuál es su elevación?
Un ave marina se encuentra a 28 metros sobre la superficie del océano. ¿Cuál es su elevación?
Si el ave está directamente encima del pez, ¿a qué distancia están?

Ejercicio$\PageIndex{7}$

Compare usando >, = o <.

$3$_____$-3$
$12$_____$24$
$-12$_____$-24$
$5$_____$-(-5)$
$7.2$_____$7$
$-7.2$_____$-7$
$-1.5$_____$\frac{-3}{2}$
$\frac{-4}{5}$_____$\frac{-5}{4}$
$\frac{-3}{5}$_____$\frac{-6}{10}$
$\frac{-2}{3}$_____$\frac{1}{3}$

Ejercicio$\PageIndex{8}$

Han quiere comprar un boleto de $30 para un juego, pero los boletos de pre-orden están agotados. Sabe que habrá más boletos vendidos el día del juego, con un margen de beneficio del 200%. ¿Cuánto debería esperar Han pagar por el boleto si lo compra el día del juego?

(De la Unidad 4.2.2)

Ejercicio$\PageIndex{9}$

Un tipo de pintura verde se hace mezclando 2 tazas de amarillo con 3.5 tazas de azul.

Encuentra una mezcla que haga el mismo tono de verde pero una cantidad menor.
Encuentra una mezcla que haga el mismo tono de verde pero una cantidad mayor.
Encuentra una mezcla que haga un tono diferente de verde que sea más azul.
Encuentra una mezcla que haga un tono diferente de verde que sea más amarillo.

(De la Unidad 2.1.1)

Search

Text Color

Text Size

Margin Size

Font Type