1.5: Transformación de funciones

Última actualización
Guardar como PDF

Page ID: 121393

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Funciones gráficas utilizando desplazamientos verticales y horizontales.
Funciones gráficas usando reflexiones sobre el eje x y el eje y.
Determine si una función es par, impar o ninguna de sus gráficas.
Funciones gráficas usando compresiones y estiramientos.
Combinar transformaciones.

Todos sabemos que un espejo plano nos permite ver una imagen precisa de nosotros mismos y de lo que haya detrás de nosotros. Cuando inclinamos el espejo, las imágenes que vemos pueden desplazarse horizontal o verticalmente. Pero, ¿qué pasa cuando doblamos un espejo flexible? Al igual que un espejo de carnaval, nos presenta una imagen distorsionada de nosotros mismos, estirada o comprimida horizontal o verticalmente. De manera similar, podemos distorsionar o transformar funciones matemáticas para adaptarlas mejor a describir objetos o procesos en el mundo real. En esta sección, vamos a echar un vistazo a varios tipos de transformaciones.

alt — Figura$\PageIndex{1}$: (crédito: “Misko” /Flickr)

A menudo, cuando se nos da un problema, tratamos de modelar el escenario usando matemáticas en forma de palabras, tablas, gráficas y ecuaciones. Un método que podemos emplear es adaptar los gráficos básicos de las funciones del kit de herramientas para construir nuevos modelos para un escenario dado. Existen formas sistemáticas de alterar funciones para construir modelos adecuados a los problemas que estamos tratando de resolver.

Identificación de desplazamientos verticales

Un tipo simple de transformación implica desplazar la gráfica completa de una función hacia arriba, hacia abajo, a la derecha o a la izquierda. El desplazamiento más simple es un desplazamiento vertical, moviendo la gráfica hacia arriba o hacia abajo, porque esta transformación implica agregar una constante positiva o negativa a la función. En otras palabras, agregamos la misma constante al valor de salida de la función independientemente de la entrada. Para una función$g(x)=f(x)+k$, la función$f(x)$ se desplaza verticalmente$k$ unidades. Ver Figura$\PageIndex{2}$ para un ejemplo.

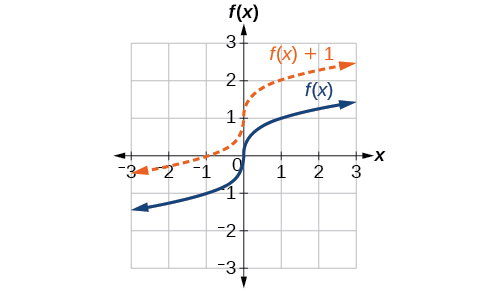
Desplazamiento vertical por k=1 de la función de raíz cúbica f (x) =3√x. — Figura$\PageIndex{2}$: Desplazamiento vertical por función$k=1$ de raíz cubo$f(x)=\sqrt[3]{x}$.

Para ayudarle a visualizar el concepto de un desplazamiento vertical, considérelo$y=f(x)$. Por lo tanto,$f(x)+k$ es equivalente a$y+k$. Cada unidad de$y$ es reemplazada por$y+k$, por lo que el$y$ -valor aumenta o disminuye dependiendo del valor de$k$. El resultado es un desplazamiento hacia arriba o hacia abajo.

Definición: Desplazamiento vertical

Dada una función$f(x)$, una nueva función$g(x)=f(x)+k$, donde$k$ es una constante, es un desplazamiento vertical de la función$f(x)$. Todos los valores de salida cambian por$k$ unidades. Si$k$ es positivo, la gráfica se desplazará hacia arriba. Si$k$ es negativo, la gráfica se desplazará hacia abajo.

Ejemplo$\PageIndex{1}$: Adding a Constant to a Function

Para regular la temperatura en un edificio verde, los respiraderos de flujo de aire cerca del techo se abren y cierran durante todo el día. La figura$\PageIndex{3}$ muestra el área de respiraderos abiertos$V$ (en pies cuadrados) a lo largo del día en horas posteriores a la medianoche,$t$. Durante el verano, el gerente de las instalaciones decide tratar de regular mejor la temperatura aumentando la cantidad de respiraderos abiertos en 20 pies cuadrados a lo largo del día y la noche. Esboza una gráfica de esta nueva función.

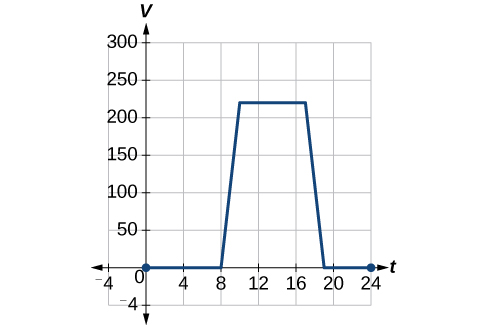
Solución

Podemos esbozar una gráfica de esta nueva función agregando 20 a cada uno de los valores de salida de la función original. Esto tendrá el efecto de desplazar la gráfica verticalmente hacia arriba, como se muestra en la Figura$\PageIndex{4}$.

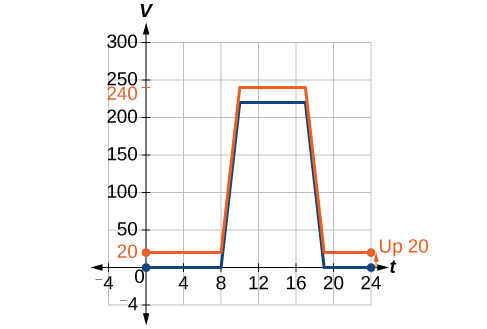
Observe que en la Figura$\PageIndex{4}$, por cada valor de entrada, el valor de salida ha aumentado en 20, así que si llamamos a la nueva función$S(t)$, podríamos escribir

\[S(t)=V(t)+20\]

Esta notación nos dice que, para cualquier valor de$t$, se$S(t)$ puede encontrar evaluando la función$V$ en la misma entrada y luego agregando 20 al resultado. Esto define$S$ como una transformación de la función$V$, en este caso un desplazamiento vertical hacia arriba de 20 unidades. Observe que, con un desplazamiento vertical, los valores de entrada permanecen iguales y solo cambian los valores de salida. Ver Tabla$\PageIndex{1}$.

Mesa$\PageIndex{1}$
$t$	0	8	10	17	19	24
$V(t)$	0	0	220	220	0	0
$S(t)$	20	20	240	240	20	20

Cómo...

Dada una función tabular, crear una nueva fila para representar un desplazamiento vertical.

Identificar la fila o columna de salida.
Determinar la magnitud del cambio.
Agregue el desplazamiento al valor en cada celda de salida. Suma un valor positivo para arriba o un valor negativo para abajo.

Ejemplo$\PageIndex{2}$: Shifting a Tabular Function Vertically

Una función$f(x)$ se da en la Tabla$\PageIndex{2}$. Crear una tabla para la función$g(x)=f(x)−3$.

Mesa$\PageIndex{2}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Solución

La fórmula nos$g(x)=f(x)−3$ dice que podemos encontrar los valores de salida de$g$ restando 3 de los valores de salida de$f$. Por ejemplo:

\[\begin{align*} f(x)&=1 &\text{Given} \\[4pt] g(x)&=f(x)-3 &\text{Given Transformation} \\[4pt] g(2) & =f(2)−3 \\ &=1-3\\ &=-2\end{align*}\]

Restando 3 de cada$f(x)$ valor, podemos completar una tabla de valores para$g(x)$ como se muestra en Tabla$\PageIndex{3}$.

Mesa$\PageIndex{3}$
$x$	2	4	6	8
$f(x)$	1	3	7	11
$g(x)$	-2	0	4	8

Análisis

Al igual que con el desplazamiento vertical anterior, observe que los valores de entrada permanecen iguales y solo cambian los valores de salida.

Ejercicio$\PageIndex{1}$

La función$h(t)=−4.9t^2+30t$ da la altura$h$ de una pelota (en metros) lanzada hacia arriba desde el suelo después de$t$ segundos. Supongamos que en cambio la pelota fue lanzada desde lo alto de un edificio de 10 m. Relacionar esta nueva función de altura$b(t)$ con$h(t)$, y luego encontrar una fórmula para$b(t)$.

Responder: $b(t)=h(t)+10=−4.9t^2+30t+10$

Identificación de los desplazamientos horizontales

Acabamos de ver que el desplazamiento vertical es un cambio a la salida, o fuera, de la función. Ahora veremos cómo los cambios a la entrada, en el interior de la función, cambian su gráfica y significado. Un desplazamiento a la entrada da como resultado un movimiento de la gráfica de la función izquierda o derecha en lo que se conoce como desplazamiento horizontal, mostrado en la Figura$\PageIndex{4}$.

alt — Figura$\PageIndex{4}$: Desplazamiento horizontal de la función$f(x)=\sqrt[3]{x}$. Tenga en cuenta que$h=-1$ desplaza la gráfica hacia la izquierda, es decir, hacia valores negativos de$x$.

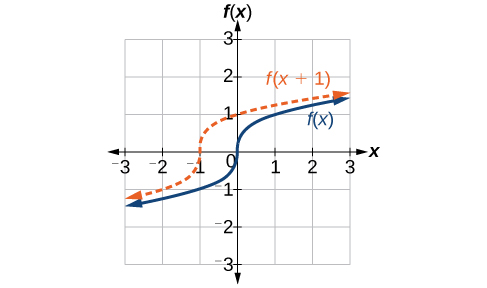
Por ejemplo, si$f(x)=x^2$, entonces$g(x)=(x−2)^2$ es una nueva función. Cada entrada se reduce en 2 antes de cuadrar la función. El resultado es que la gráfica se desplaza 2 unidades hacia la derecha, porque necesitaríamos aumentar la entrada anterior en 2 unidades para producir el mismo valor de salida que se da en$f$.

Definición: Desplazamiento horizontal

Dada una función$f$, una nueva función$g(x)=f(x−h)$, donde$h$ es una constante, es un desplazamiento horizontal de la función$f$. Si$h$ es positivo, la gráfica se desplazará a la derecha. Si$h$ es negativo, la gráfica se desplazará a la izquierda.

Ejemplo$\PageIndex{4}$: Adding a Constant to an Input

Volviendo a nuestro ejemplo de flujo de aire de edificio de Figura$\PageIndex{2}$, supongamos que en otoño el gerente de instalaciones decide que el plan de ventilación original comienza demasiado tarde, y quiere comenzar todo el programa de ventilación 2 horas antes. Esboce una gráfica de la nueva función.

Solución

Podemos establecer$V(t)$ para ser el programa original y$F(t)$ para ser el programa revisado.

\[V(t)= \text{ the original venting plan} \nonumber\]

\[F(t)= \text{ starting 2 hrs sooner} \nonumber\]

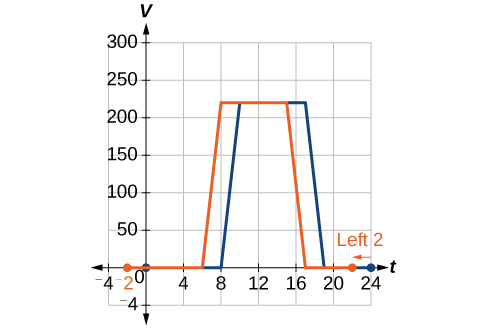
En la nueva gráfica, en cada momento, el flujo de aire es el mismo que la función original$V$ era 2 horas después. Por ejemplo, en la función original$V$, el flujo de aire comienza a cambiar a las 8 a.m., mientras que para la función$F$, el flujo de aire comienza a cambiar a las 6 a.m. Los valores de función comparables son$V(8)=F(6)$. Ver Figura$\PageIndex{5}$. Observe también que los respiraderos se abrieron por primera vez$220 \text{ft}^2$ a las 10 de la mañana bajo el plan original, mientras que bajo el nuevo plan los respiraderos llegan$220 \text{ft}^2$ a las 8 de la mañana, así$V(10)=F(8)$.

En ambos casos, vemos eso, porque$F(t)$ inicia 2 horas antes,$h=−2$. Eso significa que se alcanzan los mismos valores de salida cuando$F(t)=V(t−(−2))=V(t+2)$.

Análisis

Tenga en cuenta que$V(t+2)$ tiene el efecto de desplazar la gráfica hacia la izquierda.

Los cambios horizontales o “cambios internos” afectan el dominio de una función (la entrada) en lugar del rango y a menudo parecen contrarios a la intuición. La nueva función$F(t)$ utiliza las mismas salidas que$V(t)$, pero hace coincidir esas salidas con entradas 2 horas antes que las de$V(t)$. Dicho de otra manera, debemos sumar 2 horas a la entrada de$V$ para encontrar la salida correspondiente para$F:F(t)=V(t+2)$.

Cómo...

Dada una función tabular, cree una nueva fila para representar un desplazamiento horizontal.

Identificar la fila o columna de entrada.
Determinar la magnitud del cambio.
Agregue el desplazamiento al valor en cada celda de entrada.

Ejemplo$\PageIndex{5}$: Shifting a Tabular Function Horizontally

Una función$f(x)$ se da en la Tabla$\PageIndex{4}$. Crear una tabla para la función$g(x)=f(x−3)$.

Mesa$\PageIndex{4}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Solución

La fórmula nos$g(x)=f(x−3)$ dice que los valores de salida de$g$ son los mismos que el valor de salida de$f$ cuando el valor de entrada es 3 menor que el valor original. Por ejemplo, eso lo sabemos$f(2)=1$. Para obtener la misma salida de la función$g$, necesitaremos un valor de entrada que sea 3 mayor. Ingresamos un valor que es 3 mayor$g(x)$ porque la función quita 3 antes de evaluar la función$f$.

\[\begin{align*} g(5)&=f(5-3) \\ &=f(2) \\ &=1 \end{align*}\]

Seguimos con los otros valores para crear Tabla$\PageIndex{5}$.

Mesa$\PageIndex{5}$
$x$	5	7	9	11
$x-3$	2	4	6	8
$f(x)$	1	3	7	11
$g(x)$	1	3	7	11

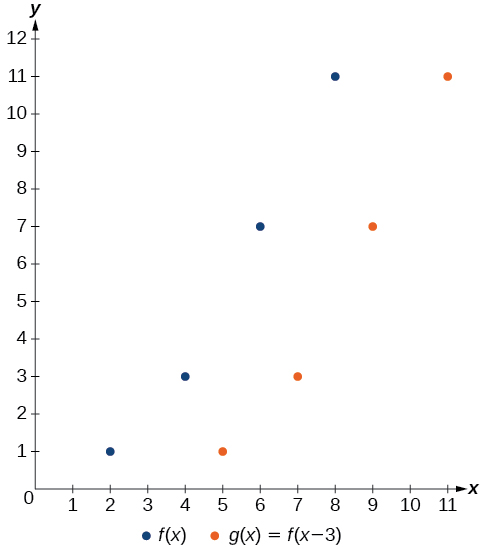
El resultado es que la función$g(x)$ ha sido desplazada a la derecha por 3. Observe que los valores de salida para$g(x)$ siguen siendo los mismos que los valores de salida para$f(x)$, pero los valores de entrada correspondientes$x$,, se han desplazado a la derecha en 3. Específicamente, 2 cambiaron a 5, 4 cambiaron a 7, 6 cambiaron a 9 y 8 cambiaron a 11.

Análisis

La figura$\PageIndex{6}$ representa ambas funciones. Podemos ver el desplazamiento horizontal en cada punto.

Gráfico de los puntos de la tabla anterior para f (x) y g (x) =f (x-3) — Figura$\PageIndex{6}$: Gráfico de los puntos de la tabla anterior para$f(x)$ y$g(x)=f(x-3)$

Ejemplo$\PageIndex{6}$: Identifying a Horizontal Shift of a Toolkit Function

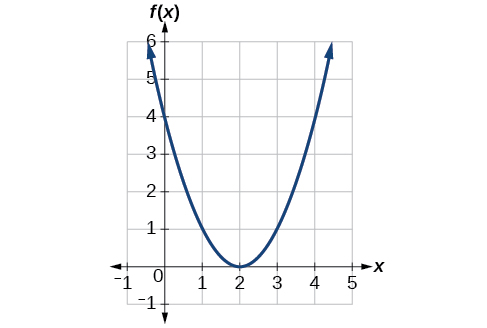
La figura$\PageIndex{7}$ representa una transformación de la función del kit de herramientas$f(x)=x^2$. Relacionar esta nueva función$g(x)$ con$f(x)$, y luego encontrar una fórmula para$g(x)$.

Figura$\PageIndex{7}$: Gráfica de una parábola

Solución

Observe que la gráfica es idéntica en forma a la$f(x)=x^2$ función, pero los$x$ valores -se desplazan hacia la derecha 2 unidades. El vértice solía estar en$(0,0)$, pero ahora el vértice está en$(2,0)$. El gráfico es la función cuadrática básica desplazada 2 unidades a la derecha, por lo que

\[g(x)=f(x−2) \nonumber\]

Observe cómo debemos ingresar el valor$x=2$ para obtener el valor de salida$y=0$; los$x$ valores -deben ser 2 unidades más grandes debido al desplazamiento hacia la derecha en 2 unidades. Entonces podemos usar la definición de la$f(x)$ función para escribir una fórmula$g(x)$ evaluando$f(x−2)$.

\[\begin{align*} f(x)&=x^2 \\ g(x)&=f(x-2) \\ g(x)&=f(x-2)=(x-2)^2 \end{align*}\]

Análisis

Para determinar si el desplazamiento es$+2$ o$−2$, considere un solo punto de referencia en la gráfica. Para una cuadrática, mirar el punto del vértice es conveniente. En la función original,$f(0)=0$. En nuestra función desplazada,$g(2)=0$. Para obtener el valor de salida de 0 de la función$f$, necesitamos decidir si un signo más o un signo menos funcionará para satisfacer$g(2)=f(x−2)=f(0)=0$. Para que esto funcione, necesitaremos restar 2 unidades de nuestros valores de entrada.

Ejemplo$\PageIndex{7}$: Interpreting Horizontal versus Vertical Shifts

La función$G(m)$ da el número de galones de gas necesarios para conducir$m$ millas. Interpretar$G(m)+10$ y$G(m+10)$

Solución

$G(m)+10$se puede interpretar como agregar 10 a la salida, galones. Este es el gas requerido para conducir$m$ millas, más otros 10 galones de gas. La gráfica indicaría un desplazamiento vertical.

$G(m+10)$se puede interpretar como agregar 10 a la entrada, millas. Entonces esta es la cantidad de galones de gas requeridos para conducir 10 millas más que$m$ millas. La gráfica indicaría un desplazamiento horizontal.

Ejercicio$\PageIndex{7}$

Dada la función$f(x)=\sqrt{x}$, grafica la función original$f(x)$ y la transformación$g(x)=f(x+2)$ en los mismos ejes. ¿Se trata de un desplazamiento horizontal o vertical? ¿De qué manera se desplaza la gráfica y por cuántas unidades?

Responder: Las gráficas de$f(x)$ y$g(x)$ se muestran a continuación. La transformación es un desplazamiento horizontal. La función se desplaza a la izquierda en 2 unidades.

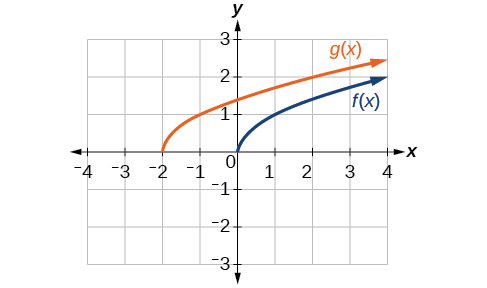
$Gráfica de una función de raíz cuadrada y una función de desplazamiento horizontal de pie cuadrado.$
Figura$\PageIndex{8}$

Combinando Desplazamientos Vertical y Horizontal

Ahora que tenemos dos transformaciones, podemos combinarlas juntas. Los desplazamientos verticales son cambios externos que afectan los valores del$(y-)$ eje de salida y desplazan la función hacia arriba o hacia abajo. Los desplazamientos horizontales son cambios internos que afectan los valores del$(x-)$ eje de entrada y desplazan la función hacia la izquierda o la derecha. Combinar los dos tipos de turnos provocará que la gráfica de una función se desplace hacia arriba o hacia abajo y hacia la derecha o la izquierda.

Cómo...

Dada una función y un desplazamiento tanto vertical como horizontal, bosquejar la gráfica.

Identificar los desplazamientos verticales y horizontales a partir de la fórmula.
El desplazamiento vertical resulta de una constante añadida a la salida. Mueva la gráfica hacia arriba para una constante positiva y hacia abajo para una constante negativa.
El desplazamiento horizontal resulta de una constante añadida a la entrada. Mueva la gráfica a la izquierda para una constante positiva y a la derecha para una constante negativa.
Aplicar los turnos a la gráfica en cualquier orden.

Ejemplo$\PageIndex{8}$: Graphing Combined Vertical and Horizontal Shifts

Dado$f(x)=|x|$, esbozar una gráfica de$h(x)=f(x+1)−3$.

Solución

La función$f$ es nuestra función de valor absoluto de kit de herramientas. Sabemos que esta gráfica tiene forma de V, con el punto en el origen. La gráfica de se$h$ ha transformado$f$ de dos maneras:$f(x+1)$ es un cambio en el interior de la función, dando un desplazamiento horizontal a la izquierda por 1, y la resta por 3 in$f(x+1)−3$ es un cambio al exterior de la función, dando un desplazamiento vertical hacia abajo por 3. La transformación de la gráfica se ilustra en la Figura$\PageIndex{9}$.

Sigamos un punto de la gráfica de$f(x)=|x|$.

El punto$(0,0)$ se transforma primero desplazando a la izquierda 1 unidad:$(0,0)\rightarrow(−1,0)$
El punto$(−1,0)$ se transforma a continuación desplazando hacia abajo 3 unidades:$(−1,0)\rightarrow(−1,−3)$

Gráfico de una función absoluta, <span translate= — Figura$\PageIndex{9}$: Gráfica de una función absoluta$y=|x|$, y cómo se transformó en$y=|x+1|-3$

La figura$\PageIndex{10}$ muestra la gráfica de$h$.

La función final <span translate= — Figura$\PageIndex{10}$: La función final$y=|x+1|-3$.

Ejercicio$\PageIndex{8}$

Dado$f(x)=|x|$, esbozar una gráfica de$h(x)=f(x−2)+4$.

Responder: $alt$
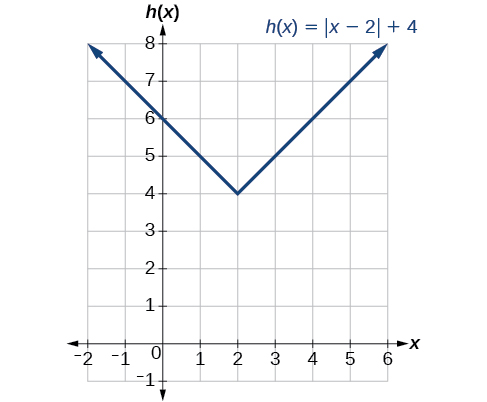
Figura$\PageIndex{11}$

Ejemplo$\PageIndex{9}$: Identifying Combined Vertical and Horizontal Shifts

Escriba una fórmula para el gráfico que se muestra en la Figura$\PageIndex{12}$, que es una transformación de la función de raíz cuadrada del kit de herramientas.

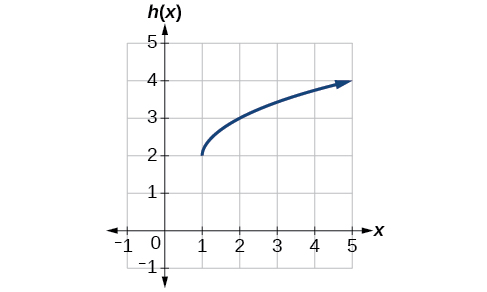
Figura$\PageIndex{12}$: Gráfica de una función de raíz cuadrada transpuesta a derecha una unidad y arriba 2.

Solución

La gráfica de la función del kit de herramientas comienza en el origen, por lo que esta gráfica se ha desplazado 1 hacia la derecha y hacia arriba 2. En notación de funciones, podríamos escribir eso como

\[h(x)=f(x−1)+2 \nonumber\]

Usando la fórmula para la función de raíz cuadrada, podemos escribir

\[h(x)=\sqrt{x−1}+2 \nonumber\]

Análisis

Tenga en cuenta que esta transformación ha cambiado el dominio y el rango de la función. Esta nueva gráfica tiene dominio$\left[1,\infty\right)$ y rango$\left[2,\infty\right)$.

Ejercicio$\PageIndex{9}$

Escriba una fórmula para una transformación de la función recíproca del kit de herramientas$f(x)=\frac{1}{x}$ que desplace la gráfica de la función una unidad a la derecha y una unidad hacia arriba.

Responder: \[g(x)=\dfrac{1}{x-1}+1 \nonumber \]

Graficar funciones usando reflexiones sobre los ejes

Otra transformación que se puede aplicar a una función es una reflexión sobre el eje x o y. Una reflexión vertical refleja una gráfica verticalmente a través del eje x, mientras que una reflexión horizontal refleja una gráfica horizontalmente a través del eje y. Las reflexiones se muestran en la Figura$\PageIndex{13}$.

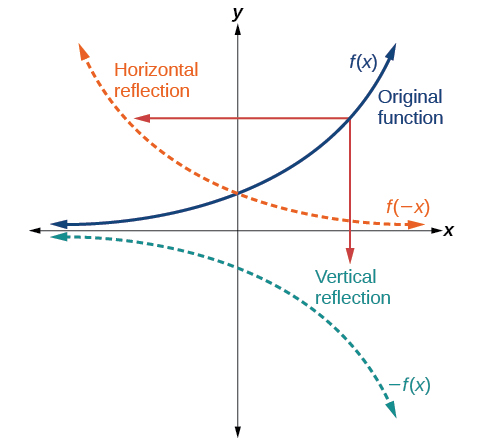Figura$\PageIndex{13}$: Gráfica de la reflexión vertical y horizontal de una función.

Observe que la reflexión vertical produce una nueva gráfica que es una imagen especular de la base o gráfica original alrededor del eje x. La reflexión horizontal produce una nueva gráfica que es una imagen especular de la base o gráfica original alrededor del eje y.

Definiciones: Reflexiones

Dada una función$f(x)$, una nueva función$g(x)=−f(x)$ es una reflexión vertical de la función$f(x)$, a veces llamada reflexión sobre (o sobre, o a través de) el eje x.

Dada una función$f(x)$, una nueva función$g(x)=f(−x)$ es una reflexión horizontal de la función$f(x)$, a veces llamada reflexión sobre el eje y.

Cómo...

Dada una función, reflejar la gráfica tanto vertical como horizontalmente.

Multiplique todas las salidas por —1 para una reflexión vertical. La nueva gráfica es un reflejo de la gráfica original sobre el eje x.
Multiplique todas las entradas por —1 para una reflexión horizontal. La nueva gráfica es un reflejo de la gráfica original sobre el eje y.

Ejemplo$\PageIndex{10}$: Reflecting a Graph Horizontally and Vertically

Reflejar la gráfica de$s(t)=\sqrt{t}$ (a) verticalmente y (b) horizontalmente.

Solución

a. Reflejar la gráfica verticalmente significa que cada valor de salida se reflejará sobre el eje t horizontal como se muestra en la Figura$\PageIndex{14}$.

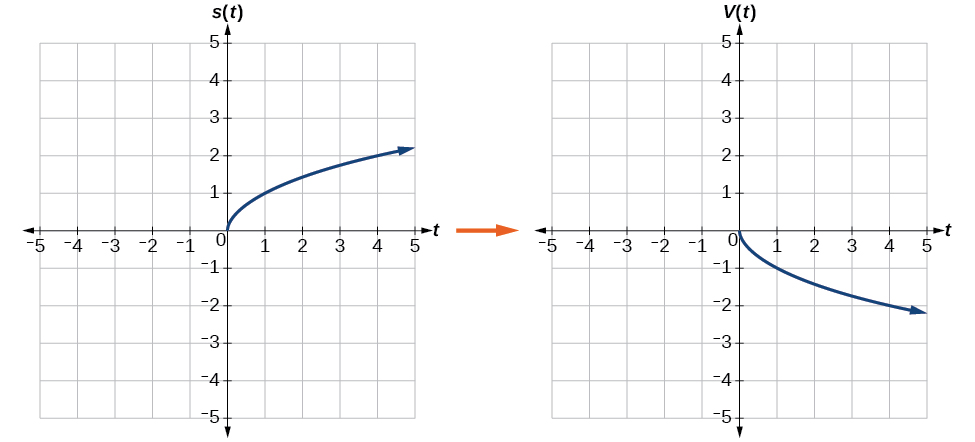
Figura$\PageIndex{14}$: Gráfica de la reflexión vertical de la función raíz cuadrada.

Debido a que cada valor de salida es lo opuesto al valor de salida original, podemos escribir

\[V(t)=−s(t) \text{ or } V(t)=−\sqrt{t} \nonumber\]

Observe que se trata de un cambio externo, o desplazamiento vertical, que afecta a los$s(t)$ valores de salida, por lo que el signo negativo pertenece fuera de la función.

b. Reflejar horizontalmente significa que cada valor de entrada se reflejará sobre el eje vertical como se muestra en la Figura$\PageIndex{15}$.

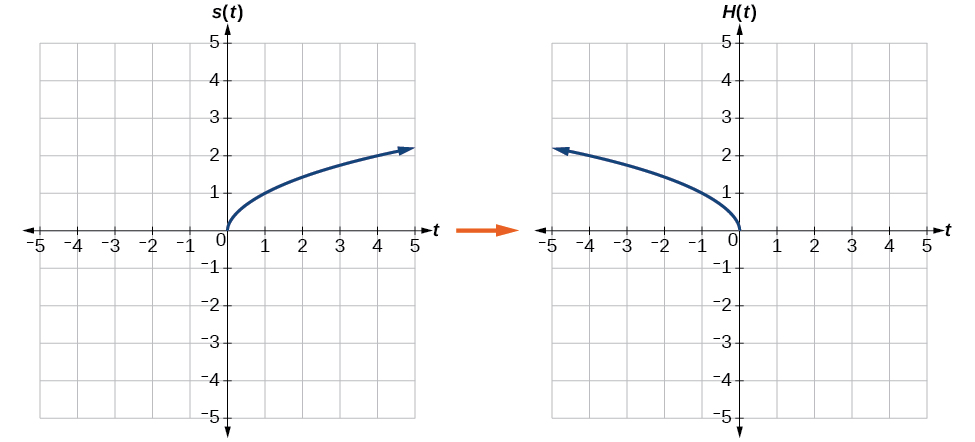
Gráfica de la reflexión horizontal de la función raíz cuadrada. — Figura$\PageIndex{15}$: Reflejo horizontal de la función raíz cuadrada

Debido a que cada valor de entrada es lo opuesto al valor de entrada original, podemos escribir

\[H(t)=s(−t) \text{ or } H(t)=\sqrt{−t} \nonumber\]

Observe que se trata de un cambio interior o cambio horizontal que afecta a los valores de entrada, por lo que el signo negativo está en el interior de la función.

Tenga en cuenta que estas transformaciones pueden afectar el dominio y rango de las funciones. Mientras que la función raíz cuadrada original tiene dominio$\left[0,\infty\right)$ y rango$\left[0,\infty\right)$, la reflexión vertical le da a la$V(t)$ función el rango$\left(−\infty,0\right]$ y la reflexión horizontal le da a la$H(t)$ función el dominio$\left(−\infty, 0\right]$.

Ejercicio$\PageIndex{5}$

Reflejar la gráfica de$f(x)=|x−1|$ (a) verticalmente y (b) horizontalmente.

Responder

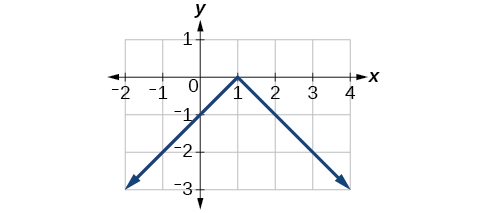
Figura$\PageIndex{16}$: Gráfica de una función absoluta reflejada verticalmente.

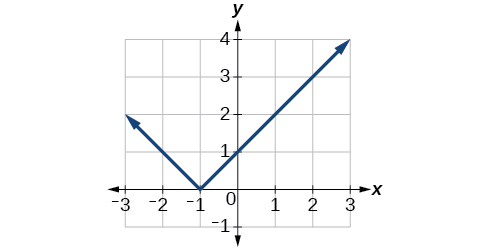
Gráfica de una función absoluta traducida una unidad izquierda. — Figura$\PageIndex{17}$: Gráfica de una función absoluta traducida una unidad a la izquierda.

Ejemplo$\PageIndex{11}$: Reflecting a Tabular Function Horizontally and Vertically

Una función$f(x)$ se da como Tabla$\PageIndex{6}$. Cree una tabla para las funciones que aparecen a continuación.

a.$g(x)=−f(x)$
b.$h(x)=f(−x)$

Mesa$\PageIndex{6}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

a. para$g(x)$, el signo negativo fuera de la función indica una reflexión vertical, por lo que los valores x permanecen iguales y cada valor de salida será el opuesto al valor de salida original. Ver Tabla$\PageIndex{7}$.

Mesa$\PageIndex{7}$
$x$	2	4	6	8
$g(x)$	-1	-3	-7	-11

b. para$h(x)$, el signo negativo dentro de la función indica una reflexión horizontal, por lo que cada valor de entrada será el opuesto al valor de entrada original y los$h(x)$ valores permanecerán iguales que los$f(x)$ valores. Ver Tabla$\PageIndex{8}$.

Mesa$\PageIndex{8}$
$x$	-2	-4	-6	-8
$h(x)$	1	3	7	11

Ejercicio$\PageIndex{6}$

Una función$f(x)$ se da como Tabla$\PageIndex{9}$. Cree una tabla para las funciones que aparecen a continuación.

a.$g(x)=−f(x)$
b.$h(x)=f(−x)$

Mesa$\PageIndex{9}$
$x$	-2	0	2	4
$f(x)$	5	10	15	20

Responder

a.$g(x)=−f(x)$

Mesa$\PageIndex{10}$
$x$	-2	0	2	4
$g(x)$	-5	-10	-15	-20

b.$h(x)=f(−x)$

Mesa$\PageIndex{11}$
$x$	-2	0	2	-4
$h(x)$	15	10	5	20

Ejemplo$\PageIndex{12}$: Applying a Learning Model Equation

Un modelo común para el aprendizaje tiene una ecuación similar a$k(t)=−2^{−t}+1$, donde$k$ está el porcentaje de dominio que se puede lograr después de las sesiones de$t$ práctica. Esta es una transformación de la función$f(t)=2^t$ mostrada en la Figura$\PageIndex{18}$. Esbozar una gráfica de$k(t)$.

Gráfico de <span translate= — Figura$\PageIndex{18}$: Gráfica de$k(t)$

Solución

Esta ecuación combina tres transformaciones en una sola ecuación.

Una reflexión horizontal:$f(−t)=2^{−t}$
Una reflexión vertical:$−f(−t)=−2^{−t}$
Un desplazamiento vertical:$−f(−t)+1=−2^{−t}+1$

Podemos esbozar una gráfica aplicando estas transformaciones una a la vez a la función original. Sigamos dos puntos a través de cada una de las tres transformaciones. Nosotros elegiremos los puntos$(0, 1)$ y$(1, 2)$.

Primero, aplicamos una reflexión horizontal:$(0, 1) \; (–1, 2)$.
Entonces, aplicamos una reflexión vertical:$(0, −1) \; (-1, –2)$.
Finalmente, aplicamos un desplazamiento vertical:$(0, 0) \; (-1, -1)$.

Esto significa que los puntos originales,$(0,1)$ y$(1,2)$ se convierten$(0,0)$ y$(-1,-1)$ después aplicamos las transformaciones.

En la Figura$\PageIndex{19}$, la primera gráfica resulta de una reflexión horizontal. El segundo resulta de una reflexión vertical. El tercero resulta de un desplazamiento vertical hacia arriba 1 unidad.

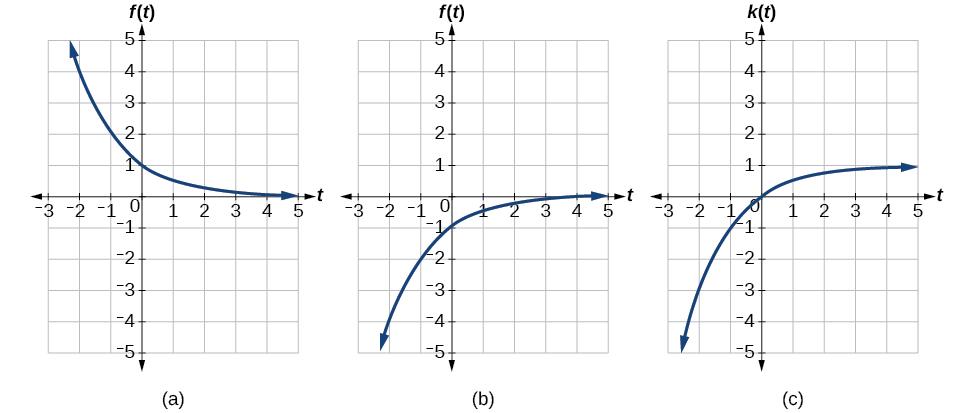
Figura$\PageIndex{19}$: Gráficas de todas las transformaciones.

Análisis

Como modelo de aprendizaje, esta función estaría limitada a un dominio de$t\geq0$, con rango correspondiente$\left[0,1\right)$.

Ejercicio$\PageIndex{7}$

Dada la función del kit de herramientas$f(x)=x^2$, gráfico$g(x)=−f(x)$ y$h(x)=f(−x)$. Toma nota de cualquier comportamiento sorprendente para estas funciones.

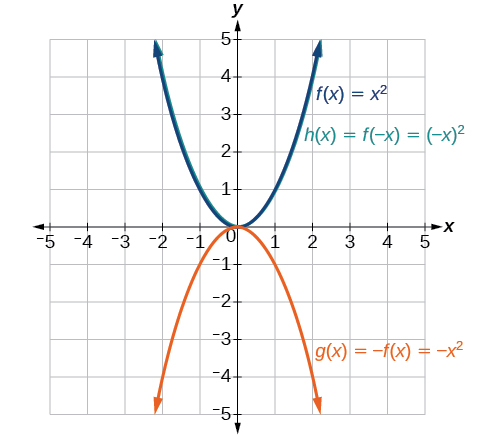
Responder: $Gráfica de x^2 y sus reflexiones.$
Figura$\PageIndex{20}$: Gráfica de$x^2$ y sus reflexiones.

Aviso:$g(x)=f(−x)$ se ve igual que$f(x)$.

Determinación de funciones pares e impares

Algunas funciones exhiben simetría para que las reflexiones resulten en la gráfica original. Por ejemplo, reflejando horizontalmente las funciones del kit de herramientas$f(x)=x^2$ o$f(x)=|x|$ resultará en la gráfica original. Decimos que este tipo de gráficas son simétricas alrededor del eje y. Las funciones cuyas gráficas son simétricas alrededor del eje y se denominan funciones pares.

Si las gráficas de$f(x)=x^3$ o$f(x)=\frac{1}{x}$ se reflejaran sobre ambos ejes, el resultado sería la gráfica original, como se muestra en la Figura$\PageIndex{21}$.

Decimos que estas gráficas son simétricas sobre el origen. Una función con una gráfica que es simétrica sobre el origen se denomina función impar.

Nota: Una función no puede ser ni par ni impar si no presenta ninguna simetría. Por ejemplo, no$f(x)=2^x$ es ni par ni impar. Además, la única función que es a la vez par e impar es la función constante$f(x)=0$.

Definiciones: Funciones pares e impares

Una función se llama función par si por cada entrada$x$

$f(x)=f(−x)$

La gráfica de una función par es simétrica alrededor del eje y.

Una función se llama una función impar si por cada entrada$x$

$f(x)=−f(−x)$

La gráfica de una función impar es simétrica sobre el origen.

Cómo...

Dada la fórmula para una función, determine si la función es par, impar o ninguna.

Determinar si la función satisface$f(x)=f(−x)$. Si lo hace, es parejo.
Determinar si la función satisface$f(x)=−f(−x)$. Si lo hace, es extraño.
Si la función no satisface ninguna regla, no es ni par ni impar.

Ejemplo$\PageIndex{13}$: Determining whether a Function Is Even, Odd, or Neither

¿La función es$f(x)=x^3+2x$ par, impar o ninguna?

Solución

Sin mirar una gráfica, podemos determinar si la función es par o impar encontrando fórmulas para las reflexiones y determinando si nos devuelven a la función original. Empecemos por la regla para funciones pares.

\[f(−x)=(−x)^3+2(−x)=−x^3−2x \nonumber\]

Esto no nos devuelve a la función original, por lo que esta función no es parejo. Ahora podemos probar la regla para funciones impares.

\[−f(−x)=−(−x^3−2x)=x^3+2x \nonumber\]

Porque$−f(−x)=f(x)$, esta es una función impar.

Análisis

Considera la gráfica de$f$ en la Figura$\PageIndex{22}$. Observe que la gráfica es simétrica sobre el origen. Por cada punto$(x,y)$ de la gráfica, el punto correspondiente también$(−x,−y)$ está en la gráfica. Por ejemplo,$(1, 3)$ está en la gráfica de$f$, y el punto correspondiente también$(−1,−3)$ está en la gráfica.

Ejercicio$\PageIndex{8}$

¿La función es$f(s)=s^4+3s^2+7$ par, impar o ninguna?

Responder: incluso

Graficar funciones usando estiramientos y compresiones

Agregar una constante a las entradas o salidas de una función cambió la posición de una gráfica con respecto a los ejes, pero no afectó la forma de una gráfica. Ahora exploramos los efectos de multiplicar las entradas o salidas por alguna cantidad.

Podemos transformar el interior (valores de entrada) de una función o podemos transformar el exterior (valores de salida) de una función. Cada cambio tiene un efecto específico que se puede ver gráficamente.

Estiramientos Verticales y Compresiones

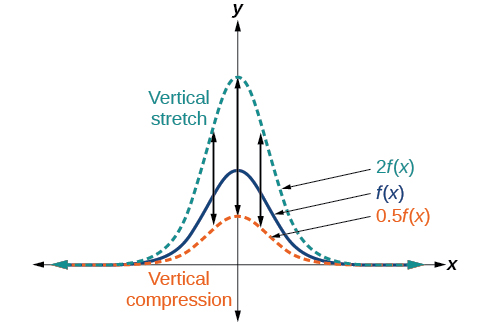
Cuando multiplicamos una función por una constante positiva, obtenemos una función cuya gráfica se estira o comprime verticalmente en relación con la gráfica de la función original. Si la constante es mayor que 1, obtenemos un estiramiento vertical; si la constante está entre 0 y 1, obtenemos una compresión vertical. La figura$\PageIndex{23}$ muestra una función multiplicada por los factores constantes 2 y 0.5 y el estiramiento vertical resultante y compresión.

Gráfica de una función que muestra estiramiento vertical y compresión. — Figura$\PageIndex{23}$: Estiramiento vertical y compresión

Definiciones: Estiramientos verticales y compresiones

Dada una función$f(x)$, una nueva función$g(x)=af(x)$, donde$a$ es una constante, es un estiramiento vertical o compresión vertical de la función$f(x)$.

Si$a>1$, entonces la gráfica se estirará.
Si$0<a<1$, entonces la gráfica se comprimirá.
Si$a<0$, entonces habrá combinación de un estiramiento vertical o compresión con una reflexión vertical.

Cómo...

Dada una función, grafica su estiramiento vertical.

Identificar el valor de$a$.
Multiplicar todos los valores de rango por$a$
Si$a>1$, la gráfica se estira por un factor de$a$.
Si$0<a<1$, la gráfica se comprime por un factor de$a$.
Si$a<0$, la gráfica se estira o comprime y también se refleja alrededor del eje x.

Ejemplo 1.5.14: Graficando un Estiramiento Vertical

Una función$P(t)$ modela la población de moscas de la fruta. La gráfica se muestra en la Figura$\PageIndex{24}$.

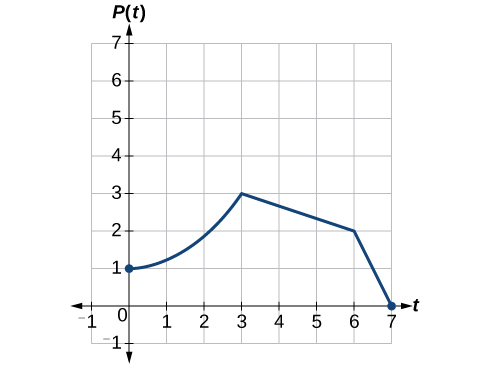
Figura$\PageIndex{24}$: Gráfica para representar el crecimiento de la población de moscas de la fruta.

Un científico está comparando esta población con otra población,$Q$, cuyo crecimiento sigue el mismo patrón, pero es el doble de grande. Esbozar una gráfica de esta población.

Solución

Debido a que la población es siempre el doble de grande, los valores de salida de la nueva población siempre son el doble de los valores de salida de la función original. Gráficamente, esto se muestra en la Figura$\PageIndex{25}$.

Si elegimos cuatro puntos de referencia$(0, 1)$,$(3, 3)$,,$(6, 2)$ y$(7, 0)$ multiplicaremos todas las salidas por 2.

A continuación se muestra dónde se ubicarán los nuevos puntos para la nueva gráfica.

\[(0, 1)\rightarrow(0, 2)\]

\[(3, 3)\rightarrow(3, 6)\]

\[(6, 2)\rightarrow(6, 4)\]

\[(7, 0)\rightarrow(7, 0)\]

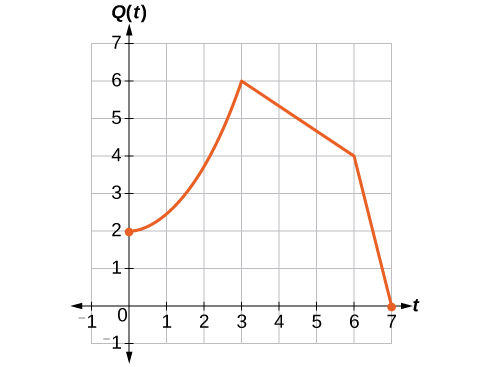
Gráfico de la función poblacional se duplicó. — Figura$\PageIndex{25}$: Gráfico de la función poblacional duplicada.

Simbólicamente, la relación se escribe como

\[Q(t)=2P(t) \nonumber\]

Esto significa que para cualquier entrada$t$, el valor de la función$Q$ es el doble del valor de la función$P$. Observe que el efecto sobre la gráfica es un estiramiento vertical de la gráfica, donde cada punto duplica su distancia con respecto al eje horizontal. Los valores de entrada,$t$, permanecen iguales mientras que los valores de salida son dos veces más grandes que antes.

Cómo...

Dada una función tabular y asumiendo que la transformación es un estiramiento o compresión vertical, crear una tabla para una compresión vertical.

Determinar el valor de$a$.
Multiplique todos los valores de salida por$a$.

Ejemplo$\PageIndex{15}$: Finding a Vertical Compression of a Tabular Function

Una función$f$ se da como Tabla$\PageIndex{12}$. Crear una tabla para la función$g(x)=\frac{1}{2}f(x)$.

Mesa$\PageIndex{12}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

Solución

La fórmula nos$g(x)=\frac{1}{2}f(x)$ dice que los valores de salida de$g$ son la mitad de los valores de salida de$f$ con las mismas entradas. Por ejemplo, eso lo sabemos$f(4)=3$. Entonces

\[g(4)=\frac{1}{2}f(4)=\frac{1}{2}(3)=\frac{3}{2} \nonumber\]

Hacemos lo mismo para los otros valores para producir Tabla$\PageIndex{13}$.

Mesa$\PageIndex{13}$
$x$	2	4	6	8
$g(x)$	$\dfrac{1}{2}$	$\dfrac{3}{2}$	$\dfrac{7}{2}$	$\dfrac{11}{2}$

Análisis

El resultado es que la función$g(x)$ ha sido comprimida verticalmente por$\frac{1}{2}$. Cada valor de salida se divide por la mitad, por lo que la gráfica es la mitad de la altura original.

Ejercicio$\PageIndex{9}$

Una función$f$ se da como Tabla$\PageIndex{14}$. Crear una tabla para la función$g(x)=\frac{3}{4}f(x)$.

Mesa$\PageIndex{14}$
$x$	2	4	6	8
$f(x)$	12	16	20	0

Responder

Mesa$\PageIndex{15}$
$x$	2	4	6	8
$g(x)$	9	12	15	0

Ejemplo$\PageIndex{16}$: Recognizing a Vertical Stretch

El gráfico en la Figura$\PageIndex{26}$ es una transformación de la función del kit de herramientas$f(x)=x^3$. Relacionar esta nueva función$g(x)$ con$f(x)$, y luego encontrar una fórmula para$g(x)$.

[Gráfico de una transformación de <span translate= — Figura$\PageIndex{26}$: Gráfica de una transformación de$f(x)=x^3$

Al intentar determinar un estiramiento o desplazamiento vertical, es útil buscar un punto en la gráfica que sea relativamente claro. En esta gráfica, aparece que$g(2)=2$. Con la función cúbica básica en la misma entrada,$f(2)=2^3=8$. En base a eso, parece que las salidas de$g$ son$\frac{1}{4}$ las salidas de la función$f$ porque$g(2)=\frac{1}{4}f(2)$. A partir de esto podemos concluir eso con bastante seguridad$g(x)=\frac{1}{4}f(x)$.

Podemos escribir una fórmula para$g$ usando la definición de la función$f$.

\[g(x)=\frac{1}{4} f(x)=\frac{1}{4}x^3.\]

Ejercicio$\PageIndex{1}$

Escribe la fórmula para la función que obtenemos cuando estiramos la función del kit de herramientas de identidad en un factor de 3, y luego la desplazamos hacia abajo en 2 unidades.

Responder: $g(x)=3x-2$

Estiramientos y Compresiones Horizontales

Ahora consideramos cambios en el interior de una función. Cuando multiplicamos la entrada de una función por una constante positiva, obtenemos una función cuya gráfica se estira o comprime horizontalmente en relación con la gráfica de la función original. Si la constante está entre 0 y 1, obtenemos un estiramiento horizontal; si la constante es mayor que 1, obtenemos una compresión horizontal de la función.

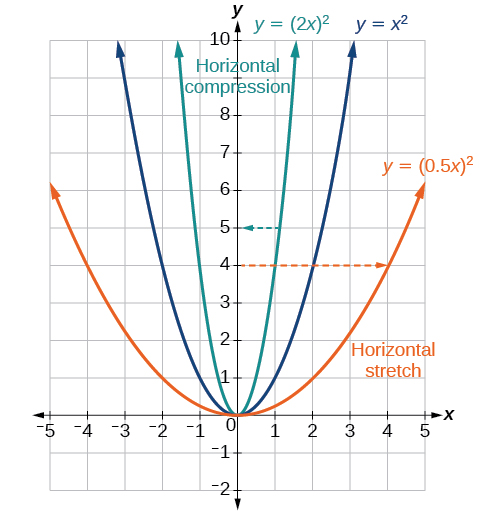
Gráfica del estiramiento vertical y compresión de x^2. — Figura$\PageIndex{27}$: Gráfica del estiramiento vertical y compresión de$x^2$.

Dada una función$y=f(x)$, la forma$y=f(bx)$ da como resultado un estiramiento o compresión horizontal. Considera la función$y=x^2$. Observar Figura$\PageIndex{27}$. La gráfica de$y=(0.5x)^2$ es un tramo horizontal de la gráfica de la función$y=x^2$ por un factor de 2. La gráfica de$y=(2x)^2$ es una compresión horizontal de la gráfica de la función$y=x^2$ por un factor de 2.

Definiciones: Estiramientos y Compresiones Horizontales

Dada una función$f(x)$, una nueva función$g(x)=f(bx)$, donde$b$ es una constante, es un estiramiento horizontal o compresión horizontal de la función$f(x)$.

Si$b>1$, entonces la gráfica será comprimida por$\frac{1}{b}$.
Si$0<b<1$, entonces la gráfica se estirará por$\frac{1}{b}$.
Si$b<0$, entonces habrá combinación de un estiramiento o compresión horizontal con una reflexión horizontal.

Cómo...

Dada una descripción de una función, esbozar una compresión o estiramiento horizontal.

Escribe una fórmula para representar la función.
Establecer$g(x)=f(bx)$ donde$b>1$ para una compresión o$0<b<1$ para un estiramiento.

Ejemplo$\PageIndex{17}$: Graphing a Horizontal Compression

Supongamos que un científico está comparando una población de moscas de la fruta con una población que progresa a lo largo de su vida dos veces más rápida que la población original. Es decir, esta nueva población,$R$, avanzará en 1 hora la misma cantidad que lo hace la población original en 2 horas, y en 2 horas, avanzará tanto como lo hace la población original en 4 horas. Esbozar una gráfica de esta población.

Solución

Simbólicamente, podríamos escribir

$\begin{align} R(1)&=P(2), \\ R(2)&=P(4), &\text{and in general,} \\ R(t)&=P(2t).\end{align}$

Ver Figura$\PageIndex{28}$ para una comparación gráfica de la población original y la población comprimida.

Dos gráficas lado a lado. La primera gráfica tiene función para población original cuyo dominio es [0,7] y rango es [0,3]. El valor máximo ocurre en (3,3). La segunda gráfica tiene la misma forma que la primera excepto que es la mitad de ancha. Se trata de una gráfica de población transformada, con un dominio de [0, 3.5] y un rango de [0,3]. El máximo ocurre en (1.5, 3). — Figura$\PageIndex{28}$: (a) Gráfica poblacional original (b) Gráfica poblacional comprimida

Análisis

Tenga en cuenta que el efecto en la gráfica es una compresión horizontal donde todos los valores de entrada son la mitad de su distancia original desde el eje vertical.

Ejemplo$\PageIndex{18}$: Finding a Horizontal Stretch for a Tabular Function

Una función$f(x)$ se da como Tabla$\PageIndex{16}$. Crear una tabla para la función$g(x)=f(\frac{1}{2}x)$.

Mesa$\PageIndex{16}$
$x$	2	4	6	8
$f(x)$	1	3	7	11

La fórmula nos$g(x)=f(\frac{1}{2}x)$ dice que los valores de salida para$g$ son los mismos que los valores de salida para la función$f$ en una entrada de la mitad del tamaño. Observe que no tenemos suficiente información para determinar$g(2)$ porque$g(2)=f(\frac{1}{2}⋅2)=f(1)$, y no tenemos un valor para$f(1)$ en nuestra tabla. Nuestros valores de entrada a$g$ deberán ser dos veces más grandes para obtener entradas para$f$ que podamos evaluar. Por ejemplo, podemos determinar$g(4)$.

\[g(4)=f(\dfrac{1}{2}⋅4)=f(2)=1\]

Hacemos lo mismo para los otros valores para producir Tabla$\PageIndex{17}$.

Mesa$\PageIndex{17}$
$x$	4	8	12	16
$g(x)$	1	3	7	11

En la figura se$\PageIndex{29}$ muestran las gráficas de ambos conjuntos de puntos.

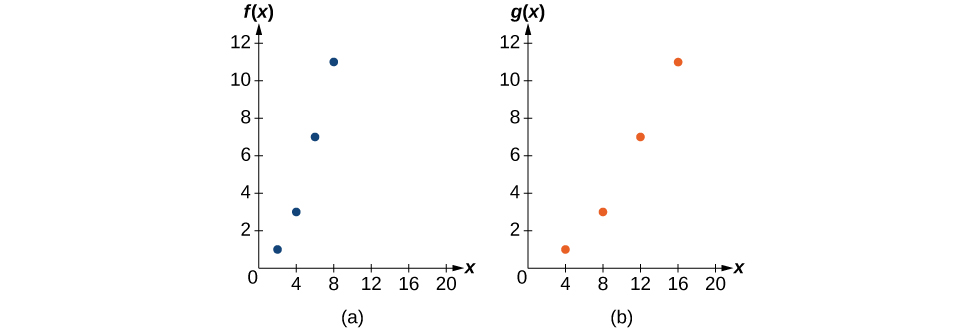
Figura$\PageIndex{29}$: Gráfica de la tabla anterior.

Análisis

Debido a que cada valor de entrada se ha duplicado, el resultado es que la función se$g(x)$ ha estirado horizontalmente por un factor de 2.

Ejemplo$\PageIndex{19}$: Recognizing a Horizontal Compression on a Graph

Relacionar la función$g(x)$ con$f(x)$ en la Figura$\PageIndex{30}$.

Solución

La gráfica de$g(x)$ se parece a la gráfica de comprimida$f(x)$ horizontalmente. Porque$f(x)$ termina en (6,4) y$g(x)$ termina en (2,4), podemos ver que los valores x han sido comprimidos por$\frac{1}{3}$, porque$6(\frac{1}{3})=2$. También podríamos notar eso$g(2)=f(6)$ y$g(1)=f(3)$. De cualquier manera, podemos describir esta relación como$g(x)=f(3x)$. Esta es una compresión horizontal por$\frac{1}{3}$.

Análisis

Observe que el coeficiente necesario para un estiramiento o compresión horizontal es el recíproco del estiramiento o compresión. Entonces, para estirar la gráfica horizontalmente por un factor de escala de 4, necesitamos un coeficiente de$\frac{1}{4}$ en nuestra función:$f(\frac{1}{4}x)$. Esto significa que los valores de entrada deben ser cuatro veces mayores para producir el mismo resultado, requiriendo que la entrada sea mayor, provocando el estiramiento horizontal.

Ejercicio$\PageIndex{11}$

Escriba una fórmula para la función de raíz cuadrada del kit de herramientas estirada horizontalmente por un factor de 3.

Responder: $g(x)=f(\frac{1}{3}x)$, por lo que usando la función de raíz cuadrada obtenemos$g(x)=\sqrt{\frac{1}{3}x}$

Realización de una Secuencia de Transformaciones

Al combinar transformaciones, es muy importante considerar el orden de las transformaciones. Por ejemplo, cambiar verticalmente 3 y luego estirar verticalmente por 2 no crea la misma gráfica que estirar verticalmente por 2 y luego desplazando verticalmente por 3, porque cuando cambiamos primero, tanto la función original como el shift se estiran, mientras que solo la función original se estira cuando nosotros estirar primero.

Cuando vemos una expresión como$2f(x)+3$, ¿con qué transformación debemos comenzar? La respuesta aquí sigue muy bien desde el orden de las operaciones. Dado el valor de salida de$f(x)$, primero multiplicamos por 2, provocando el estiramiento vertical, y luego sumamos 3, provocando el desplazamiento vertical. Es decir, multiplicar antes de la suma.

Las transformaciones horizontales son un poco más duras de pensar. Cuando escribimos$g(x)=f(2x+3)$, por ejemplo, tenemos que pensar en cómo$g$ se relacionan las entradas a la función con las entradas a la función$f$. Supongamos que sabemos$f(7)=12$. ¿Qué insumo$g$ produciría esa salida? En otras palabras, qué valor de$x$ permitirá$g(x)=f(2x+3)=12?$ Nosotros necesitaríamos$2x+3=7$. Para resolver$x$, primero restaríamos 3, resultando en un desplazamiento horizontal, y luego dividiríamos por 2, provocando una compresión horizontal.

Este formato termina siendo muy difícil de trabajar, porque suele ser mucho más fácil estirar horizontalmente una gráfica antes de cambiarla. Podemos solucionar esto factorizando dentro de la función.

\[f(bx+p)=f(b(x+\frac{p}{b})) \nonumber\]

Trabajemos a través de un ejemplo.

\[f(x)=(2x+4)^2 \nonumber\]

Podemos facturar un 2.

\[f(x)=(2(x+2))^2 \nonumber\]

Ahora podemos observar más claramente un desplazamiento horizontal hacia la izquierda 2 unidades y una compresión horizontal. Factorizar de esta manera nos permite estirar horizontalmente primero y luego desplazarnos horizontalmente.

Combinando Transformaciones

Al combinar transformaciones verticales escritas en la forma$af(x)+k$, primero estira verticalmente por$a$ y luego desplaza verticalmente por$k$.
Al combinar transformaciones horizontales escritas en la forma$f(bx+h)$, primero desplaza horizontalmente$h$ y luego estira horizontalmente por$\frac{1}{b}$.
Al combinar transformaciones horizontales escritas en la forma$f(b(x+h))$, primero estira horizontalmente por$\frac{1}{b}$ y luego desplazarlo horizontalmente por$h$.
Las transformaciones horizontales y verticales son independientes. No importa si primero se realizan transformaciones horizontales o verticales.

Ejemplo$\PageIndex{20}$: Finding a Triple Transformation of a Tabular Function

Dada Tabla$\PageIndex{18}$ para la función$f(x)$, crear una tabla de valores para la función$g(x)=2f(3x)+1$.

Mesa$\PageIndex{18}$
$x$	6	12	18	24
$f(x)$	10	14	15	17

Solución

Hay tres pasos para esta transformación, y trabajaremos de adentro hacia afuera. Comenzando con las transformaciones horizontales,$f(3x)$ es una compresión horizontal por$\frac{1}{3}$, lo que significa que multiplicamos cada$x$ -valor por$\frac{1}{3}$ .Ver Tabla$\PageIndex{19}$.

Mesa$\PageIndex{19}$
$x$	2	4	6	8
$f(3x)$	10	14	15	17

Mirando ahora a las transformaciones verticales, comenzamos con el estiramiento vertical, que multiplicará los valores de salida por 2. Esto lo aplicamos a la transformación anterior. Ver Tabla$\PageIndex{20}$.

Mesa$\PageIndex{20}$
$x$	2	4	6	8
$2f(3x)$	20	28	30	34

Finalmente, podemos aplicar el desplazamiento vertical, que agregará 1 a todos los valores de salida. Ver Tabla$\PageIndex{21}$.

Mesa$\PageIndex{21}$
$x$	2	4	6	8
$g(x)=2f(3x)+1+1$	21	29	31	35

Ejemplo$\PageIndex{21}$: Finding a Triple Transformation of a Graph

Utilice la gráfica de$f(x)$ en la Figura$\PageIndex{31}$ para bosquejar una gráfica de$k(x)=f\Big(\frac{1}{2}x+1\Big)−3$.

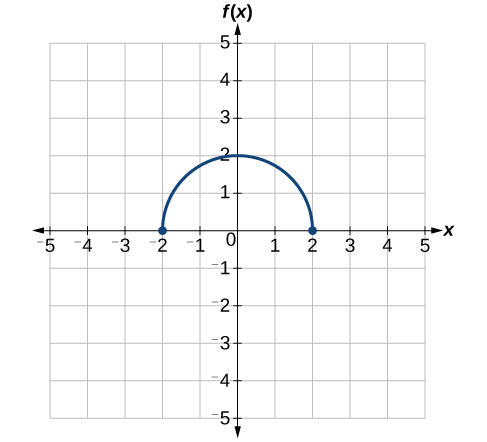
Figura$\PageIndex{31}$: Gráfica de un semicírculo.

Para simplificar, comencemos factorizando el interior de la función.

\[f\Big(\dfrac{1}{2}x+1\Big)−3=f\Big(\dfrac{1}{2}(x+2)\Big)−3\]

Al factorizar el interior, primero podemos estirar horizontalmente por 2, como lo indica el$\frac{1}{2}$ en el interior de la función. Recuerda que dos veces el tamaño de 0 sigue siendo 0, por lo que el punto$(0,2)$ permanece en$(0,2)$ mientras que el punto$(2,0)$ se estirará hasta$(4,0)$. Ver Figura$\PageIndex{32}$.

alt — Figura$\PageIndex{32}$: Gráfica de un semicírculo estirable verticalmente.

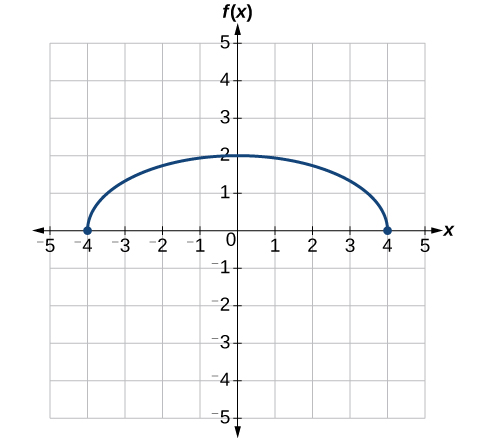
A continuación, desplazamos horizontalmente a la izquierda en 2 unidades, como lo indica$x+2$. Ver Figura$\PageIndex{33}$.

alt — Figura$\PageIndex{33}$: Gráfica de un semicírculo estirado y traducido verticalmente.

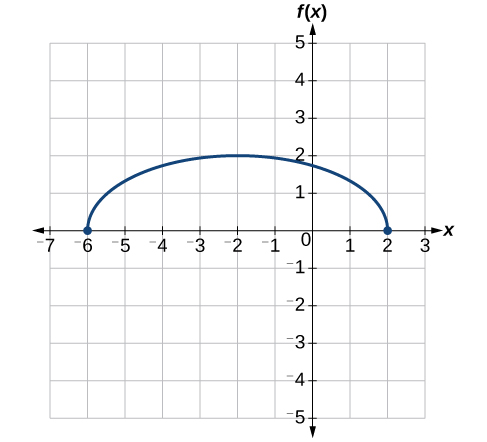
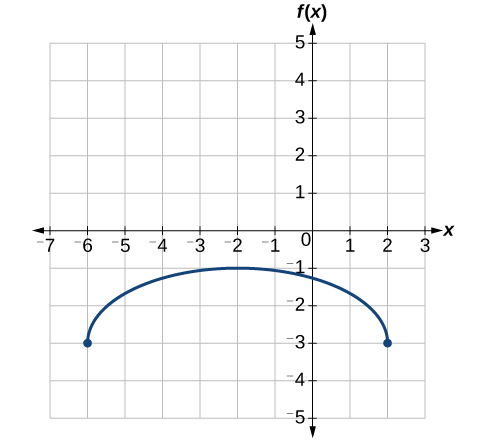
Por último, desplazamos verticalmente hacia abajo 3 para completar nuestro boceto, como lo indica el −3 en el exterior de la función. Ver Figura$\PageIndex{34}$.

alt — Figura$\PageIndex{34}$: Gráfica de un semicírculo estirado y traducido verticalmente.

Ecuaciones Clave

Desplazamiento vertical$g(x)=f(x)+k$ (arriba para$k>0$)
Desplazamiento horizontal$g(x)=f(x−h)$ (derecha) para$h>0$
Reflejo vertical$g(x)=−f(x)$
Reflejo horizontal$g(x)=f(−x)$
Estiramiento vertical$g(x)=af(x)$ (a>0)
Compresión vertical$g(x)=af(x)$ (0<a<1)
Estiramiento horizontal$g(x)=f(bx)(0<b<1)$
Compresión horizontal$g(x)=f(bx)$ (b>1)

Conceptos clave

Una función se puede desplazar verticalmente agregando una constante a la salida.
Una función se puede desplazar horizontalmente agregando una constante a la entrada.
Relacionar el cambio con el contexto de un problema permite comparar e interpretar los desplazamientos verticales y horizontales.
Los desplazamientos verticales y horizontales a menudo se combinan.
Una reflexión vertical refleja una gráfica alrededor del eje x. Un gráfico puede reflejarse verticalmente multiplicando la salida por —1.
Una reflexión horizontal refleja una gráfica alrededor del eje y. Una gráfica se puede reflejar horizontalmente multiplicando la entrada por —1.
Una gráfica se puede reflejar tanto vertical como horizontalmente. El orden en que se aplican las reflexiones no afecta a la gráfica final.
Una función presentada en forma tabular también se puede reflejar multiplicando los valores en las filas o columnas de entrada y salida en consecuencia.
Una función presentada como una ecuación puede reflejarse aplicando transformaciones una a la vez.
Las funciones pares son simétricas alrededor del eje y, mientras que las funciones impares son simétricas sobre el origen.
Incluso las funciones satisfacen la condición$f(x)=f(−x)$.
Las funciones impares satisfacen la condición$f(x)=−f(−x)$.
Una función puede ser impar, par o ninguna.
Una función puede comprimirse o estirarse verticalmente multiplicando la salida por una constante.
Una función puede comprimirse o estirarse horizontalmente multiplicando la entrada por una constante.
El orden en que se aplican las diferentes transformaciones sí afecta a la función final. Tanto las transformaciones verticales como las horizontales deben aplicarse en el orden dado. Sin embargo, una transformación vertical puede combinarse con una transformación horizontal en cualquier orden.

Glosario

incluso función

una función cuya gráfica no cambia por reflexión horizontal,$f(x)=f(−x)$, y es simétrica alrededor del eje y

compresión horizontal
una transformación que comprime la gráfica de una función horizontalmente, multiplicando la entrada por una constante b>1

reflexión horizontal
una transformación que refleja el gráfico de una función a través del eje y multiplicando la entrada por −1

desplazamiento horizontal de
una transformación que desplaza el gráfico de una función hacia la izquierda o hacia la derecha agregando una constante positiva o negativa a la entrada

horizontal estira
una transformación que estira el gráfico de una función horizontalmente multiplicando la entrada por una constante 0<b<1

función impar
una función cuya gráfica no cambia por la reflexión combinada horizontal y vertical$f(x)=−f(−x)$,, y es simétrica sobre el origen

compresión vertical
una transformación de función que comprime el gráfico de la función verticalmente multiplicando la salida por una constante 0<a<1

reflexión vertical
una transformación que refleja el gráfico de una función a través del eje x multiplicando la salida por −1

desplazamiento vertical de
una transformación que desplaza el gráfico de una función hacia arriba o hacia abajo agregando una constante positiva o negativa a la salida

estiramiento vertical
una transformación que estira el gráfico de una función verticalmente multiplicando la salida por una constante a>1

\(x\)	2	4	6	8
\(f(x)\)	1	3	7	11
\(g(x)\)	-2	0	4	8

\(x\)	5	7	9	11
\(x-3\)	2	4	6	8
\(f(x)\)	1	3	7	11
\(g(x)\)	1	3	7	11

\(x\)	2	4	6	8
\(g(x)\)	\(\dfrac{1}{2}\)	\(\dfrac{3}{2}\)	\(\dfrac{7}{2}\)	\(\dfrac{11}{2}\)

Search

Text Color

Text Size

Margin Size

Font Type

Mesa\(\PageIndex{8}\)
\(x\)	-2	-4	-6	-8
\(h(x)\)	1	3	7	11

Mesa\(\PageIndex{11}\)
\(x\)	-2	0	2	-4
\(h(x)\)	15	10	5	20

Mesa\(\PageIndex{19}\)
\(x\)	2	4	6	8
\(f(3x)\)	10	14	15	17

Mesa\(\PageIndex{20}\)
\(x\)	2	4	6	8
\(2f(3x)\)	20	28	30	34