1.R: Funciones (Revisión)
- Page ID
- 121385
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1.1: Funciones y notación de funciones
Para los ejercicios 1-4, determinar si la relación es una función.
1)\(\{(a,b),(c,d),(e,d)\}\)
- Contestar
-
función
2)\(\{(5,2),(6,1),(6,2),(4,8)\}\)
3)\(y^2+4=x\)
- Contestar
-
no es una función
4) ¿La gráfica de la siguiente figura es una función?
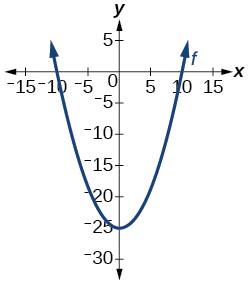
Para los ejercicios 5-6, evalúe la función a los valores indicados:\(f(-3); f(2); f(-a); -f(a); f(a+h)\)
5)\(f(x)=-2x^2+3x\)
- Contestar
-
\(f(-3)=-27; f(2)=-2;f(-a)=-2a^2-3a;-f(a)=2a^2-3a;f(a+h)=-2a^2+3a-4ah+3h-2h^2\)
6)\(f(x)=2|3x-1|\)
Para los ejercicios 7-8, determinar si las funciones son uno-a-uno.
7)\(f(x)=-3 x+5\)
- Contestar
-
uno a uno
8)\(f(x)=|x-3|\)
Para los ejercicios 9-11, utilice la prueba de línea vertical para determinar si la relación cuya gráfica se proporciona es una función.
9)
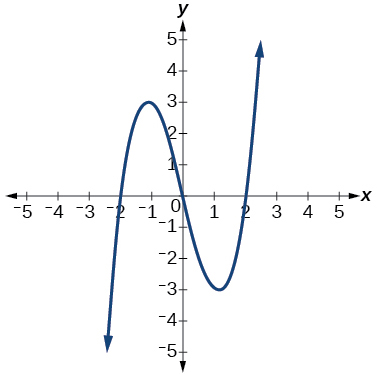
- Contestar
-
función
10)
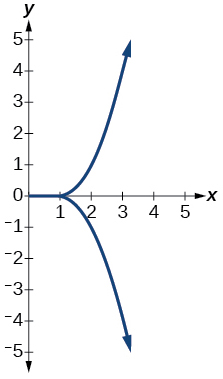
11)
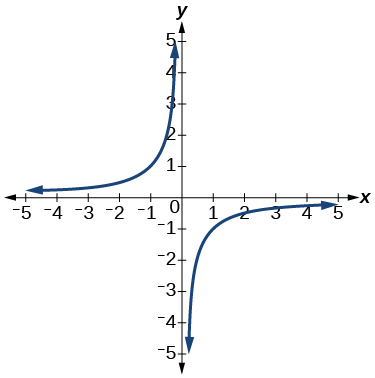
- Contestar
-
función
Para los ejercicios 12-13, grafica las funciones.
12)\(f(x)=|x+1|\)
13)\(f(x)=x^{2}-2\)
- Contestar
-
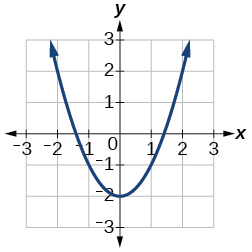
Para los ejercicios 14-17, utilice la Figura a continuación para aproximar los valores.
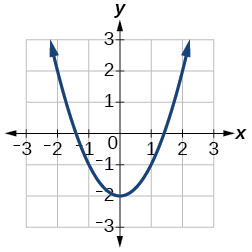
14)\(f(2)\)
15)\(f(-2)\)
- Contestar
-
\(2\)
16) Si\(f(x)=-2\), entonces resolver para\(x\)
17) Si\(f(x)=1\), entonces resolver para\(x\)
- Contestar
-
\(x=-1.8\)o\(x=1.8\)
Para los ejercicios 18-19, usa la función\(h(t)=-16 t^{2}+80t\) para encontrar los valores.
18)\(\dfrac{h(2)-h(1)}{2-1}\)
19)\(\dfrac{h(a)-h(1)}{a-1}\)
- Contestar
-
\(\dfrac{-64+80 a-16 a^{2}}{-1+a}=-16 a+64\)
1.2: Dominio y Rango
Para los ejercicios 1-4, encuentra el dominio de cada función, expresando respuestas usando notación de intervalos.
1)\(f(x)=\dfrac{2}{3 x+2}\)
2)\(f(x)=\frac{x-3}{x^{2}-4 x-12}\)
- Contestar
-
\((-\infty,-2) \cup(-2,6) \cup(6, \infty)\)
3)
4) Grafique esta función por partes:\(f(x)=\left\{\begin{array}{ll}{x+1} & {x<-2} \\ {-2 x-3} & {x \geq-2}\end{array}\right.\)
- Contestar
-
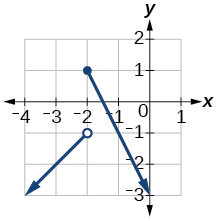
1.3: Tasas de Cambio y Comportamiento de las Gráficas
Para los ejercicios 1-3, encuentra la tasa promedio de cambio de las funciones de\(x=1\) a\(x=2\)
1)\(f(x)=4 x-3\)
2)\(f(x)=10 x^{2}+x\)
- Contestar
-
\(31\)
3)\(f(x)=-\dfrac{2}{x^{2}}\)
Para los ejercicios 4-6, utilice las gráficas para determinar los intervalos en los que las funciones están aumentando, disminuyendo o constantes.
4)
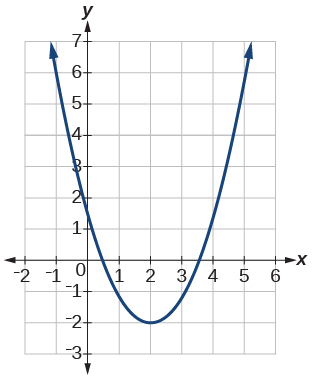
- Contestar
-
creciente\((2, \infty)\); decreciente\((-\infty, 2)\)
5)
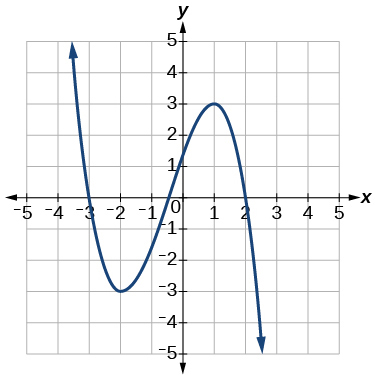
6)
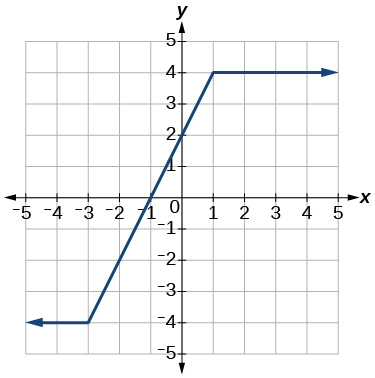
- Contestar
-
creciente\((-3,1)\); constante\((-\infty,-3) \cup(1, \infty)\)
7) Encuentra el mínimo local de la función graficada en el Ejercicio 4.
8) Encuentra los extrema locales para la función graficada en el Ejercicio 5.
- Contestar
-
mínimo local\((-2,-3)\); máximo local\((1,3)\)
9) Para la gráfica de la Figura en el Ejercicio 10, el dominio de la función es\([-3,3]\). El rango es\([-10,10]\). Encuentra el mínimo absoluto de la función en este intervalo.
10) Encuentra el máximo absoluto de la función graficada en la Figura a continuación.
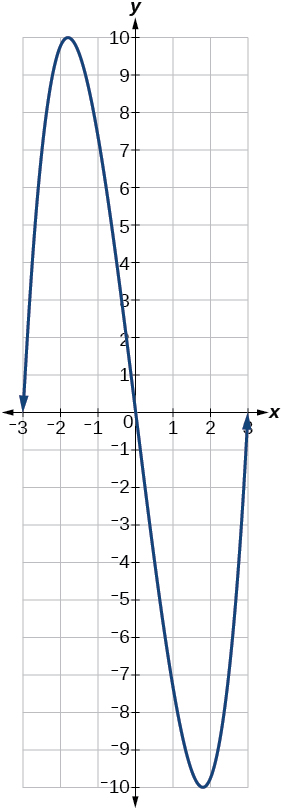
- Contestar
-
\((-1.8,10)\)
1.4: Composición de las funciones
Para los ejercicios 1-5, encuentra\((f \circ g)(x)\) y\((g \circ f)(x)\) para cada par de funciones.
1)\(f(x)=4-x, g(x)=-4x\)
2)\(f(x)=3 x+2, g(x)=5-6x\)
- Contestar
-
\((f \circ g)(x)=17-18 x ;(g \circ f)(x)=-7-18x\)
3)\(f(x)=x^{2}+2 x, g(x)=5 x+1\)
4)\(f(x)=\sqrt{x+2}, g(x)=\dfrac{1}{x}\)
- Contestar
-
\((f \circ g)(x)=\sqrt{\dfrac{1}{x}+2} ;(g \circ f)(x)=\dfrac{1}{\sqrt{x+2}}\)
5)\(f(x)=\dfrac{x+3}{2}, g(x)=\sqrt{1-x}\)
Para los ejercicios 6-9, find\((f \circ g)\) y el dominio\((f \circ g)(x)\) para cada par de funciones.
6)\(f(x)=\frac{x+1}{x+4}, g(x)=\frac{1}{x}\)
- Contestar
-
\((f \circ g)(x)=\dfrac{1+x}{1+4 x}, x \neq 0, x \neq-\dfrac{1}{4}\)
7)\(f(x)=\dfrac{1}{x+3}, g(x)=\dfrac{1}{x-9}\)
8)\(f(x)=\dfrac{1}{x}, g(x)=\sqrt{x}\)
- Contestar
-
\((f \circ g)(x)=\frac{1}{\sqrt{x}}, x>0\)
9)\(f(x)=\frac{1}{x^{2}-1}, g(x)=\sqrt{x+1}\)
Para los ejercicios 10-11, expresar cada función\(H\) como una composición de dos funciones\(f\) y\(g\) donde\(H(x)=(f \circ g)(x)\)
10)\(H(x)=\sqrt{\frac{2 x-1}{3 x+4}}\)
- Contestar
-
muestra:\(g(x)=\dfrac{2 x-1}{3 x+4}; f(x)=\sqrt{x}\)
11)\(H(x)=\dfrac{1}{\left(3 x^{2}-4\right)^{-3}}\)
1.5: Transformación de funciones
Para los ejercicios 1-8, bosquejar una gráfica de la función dada.
1)\(f(x)=(x-3)^{2}\)
- Contestar
-
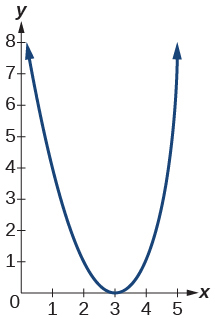
2)\(f(x)=(x+4)^{3}\)
3)\(f(x)=\sqrt{x}+5\)
- Contestar
-
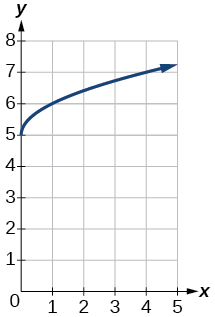
4)\(f(x)=-x^{3}\)
5)\(f(x)=\sqrt[3]{-x}\)
- Contestar
-
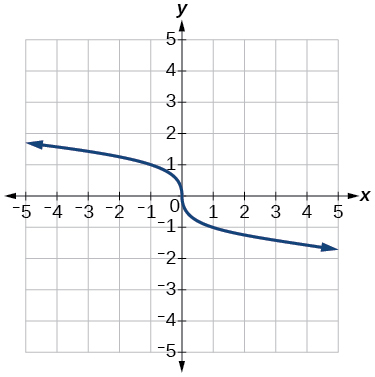
6)\(f(x)=5 \sqrt{-x}-4\)
7)\(f(x)=4[|x-2|-6]\)
- Contestar
-
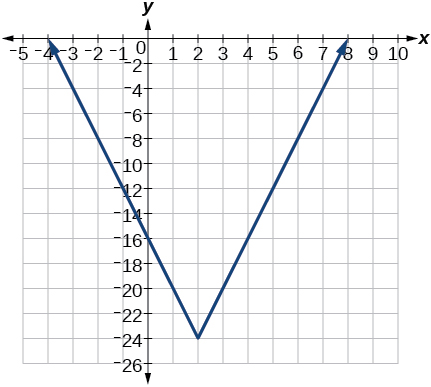
8)\(f(x)=-(x+2)^{2}-1\)
Para los ejercicios 9-10, bosquejar la gráfica de la función\(g\) si la gráfica de la función\(f\) se muestra en la Figura a continuación.
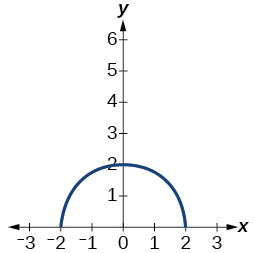
9)\(g(x)=f(x-1)\)
- Contestar
-
10)\(g(x)=3 f(x)\)
Para los ejercicios 11-12, escriba la ecuación para la función estándar representada por cada una de las gráficas a continuación.
11)
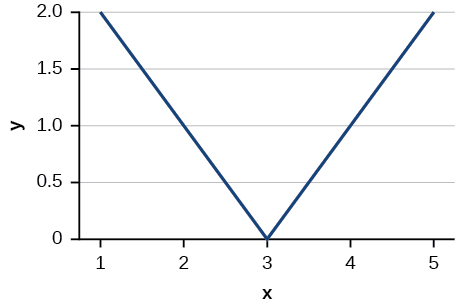
- Contestar
-
\(f(x)=|x-3|\)
12)
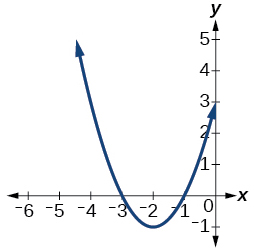
Para los ejercicios 13-15, determine si cada función a continuación es par, impar, o ninguna.
13)\(f(x)=3 x^{4}\)
- Contestar
-
incluso
14)\(g(x)=\sqrt{x}\)
15)\(h(x)=\frac{1}{x}+3 x\)
- Contestar
-
impar
Para los ejercicios 16-18, analice la gráfica y determine si la función gráfica es par, impar o ninguna.
16)
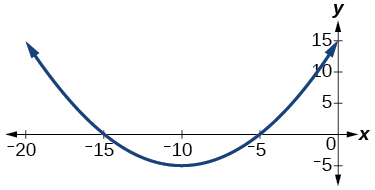
17)
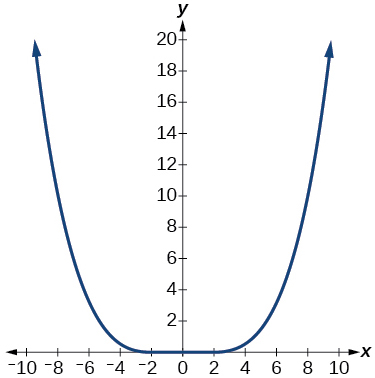
- Contestar
-
incluso
18)
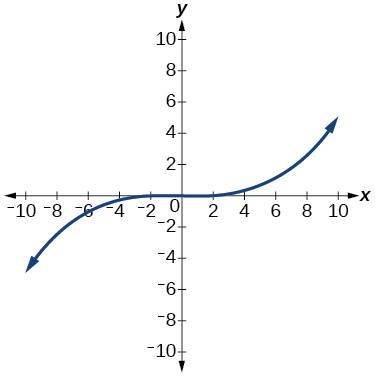
1.6: Funciones de Valor Absoluto
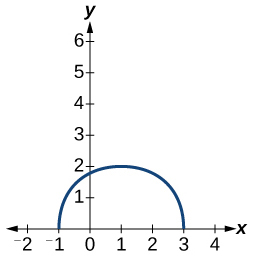
Para los ejercicios 1-3, escribir una ecuación para la transformación de\(f(x)=|x|\).
1)
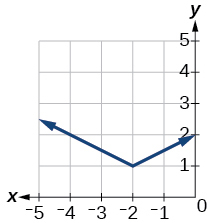
- Contestar
-
\(f(x)=\dfrac{1}{2}|x+2|+1\)
2)
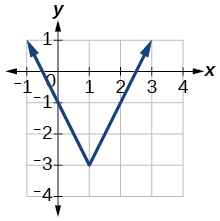
3)
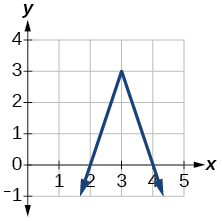
- Contestar
-
\(f(x)=-3|x-3|+3\)
Para los ejercicios 4-6, grafica la función de valor absoluto.
4)\(f(x)=|x-5|\)
5)\(f(x)=-|x-3|\)
- Contestar
-
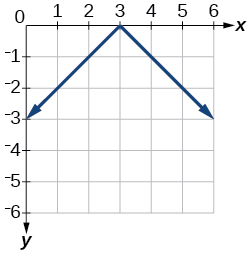
6)\(f(x)=|2 x-4|\)
Para los ejercicios 7-8, resolver la ecuación del valor absoluto.
7)\(|x+4|=18\)
- Contestar
-
\(x=-22, x=14\)
8)\(\left|\dfrac{1}{3} x+5\right|=\left|\dfrac{3}{4} x-2\right|\)
Para los ejercicios 9-10, resolver la desigualdad y expresar la solución usando notación de intervalos.
9)\(|3 x-2|<7\)
- Contestar
-
\(\left(-\dfrac{5}{3}, 3\right)\)
10)\(\left|\dfrac{1}{3} x-2\right| \leq 7\)
1.7: Funciones inversas
Para los ejercicios 1-2, encuentra\(f^{-1}(x)\) para cada función.
1)\(f(x)=9+10 x\)
2)\(f(x)=\dfrac{x}{x+2}\)
- Contestar
-
\(f^{-1}(x)=\dfrac{-2 x}{x-1}\)
3) Para el siguiente ejercicio, encontrar un dominio en el que la función\(f\) sea uno-a-uno y no decreciente. Escribe el dominio en notación de intervalos. Entonces encuentra el inverso de\(f\) restringido a ese dominio. \[f(x)=x^{2}+1\]
4) Dado\(f(x)=x^{3}-5\) y\(g(x)=\sqrt[3]{x+5} \):
- Encontrar\(f(g(x))\) y\(g(f(x))\).
- ¿Qué nos dice la respuesta sobre la relación entre\(f(x)\) y\(g(x) ?\)
- Contestar
-
- \(f(g(x))=x\)y\(g(f(x))=x\)
- Esto nos dice que\(f\) y\(g\) son funciones inversas
Para los ejercicios 5-8, utilice una utilidad gráfica para determinar si cada función es uno a uno.
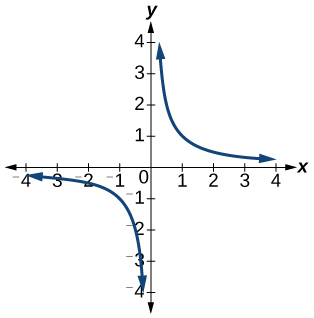
5)\(f(x)=\dfrac{1}{x}\)
- Contestar
-
La función es uno a uno.
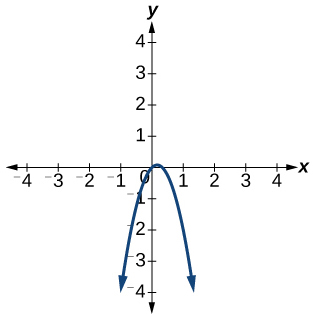
6)\(f(x)=-3 x^{2}+x\)
- Contestar
-
La función no es uno a uno.
7) Si\(f(5)=2,\) encuentra\(f^{-1}(2)\)
- Contestar
-
\(5\)
8) Si\(f(1)=4,\) encuentra\(f^{-1}(4)\)
Prueba de práctica
Para los ejercicios 1-2, determinar si cada una de las siguientes relaciones es una función.
1)\(y=2 x+8\)
- Contestar
-
La relación es una función.
2)\(\{(2,1),(3,2),(-1,1),(0,-2)\}\)
Para los ejercicios 3-4, evalúe la función\(f(x)=-3 x^{2}+2 x\) en la entrada dada.
3)\(f(-2)\)
- Contestar
-
\(-16\)
4)\(f(a)\)
5) Demostrar que la función no\(f(x)=-2(x-1)^{2}+3\) es uno a uno.
- Contestar
-
La gráfica es una parábola y la gráfica falla en la prueba de línea horizontal.
6) Escribir el dominio de la función\(f(x)=\sqrt{3-x}\) en notación de intervalos.
7) Dado\(f(x)=2 x^{2}-5 x,\) hallazgo\(f(a+1)-f(1)\)
- Contestar
-
\(2 a^{2}-a\)
8) Graficar la función\(f(x)=\left\{\begin{array}{ccc}{x+1} & {\text { if }} & {-2<x<3} \\ {-x} & {\text { if }} & {x \geq 3}\end{array}\right.\)
9) Encuentra la tasa promedio de cambio de la función\(f(x)=3-2 x^{2}+x\) encontrando\(\dfrac{f(b)-f(a)}{b-a}\)
- Contestar
-
\(-2(a+b)+1\)
Para los ejercicios 10-11, utilice las funciones\(f(x)=3-2 x^{2}+x\) y\(g(x)=\sqrt{x}\) para encontrar las funciones compuestas.
10)\((g \circ f)(x)\)
11)\((g \circ f)(1)\)
- Contestar
-
\(\sqrt{2}\)
12) Expresar\(H(x)=\sqrt[3]{5 x^{2}-3 x}\) una composición de dos funciones,\(f\) y\(g,\) donde\((f \circ g)(x)=H(x)\)
Para los ejercicios 13-14, grafica las funciones traduciendo, estirando y/o comprimiendo una función de kit de herramientas.
13)\(f(x)=\sqrt{x+6}-1\)
- Contestar
-
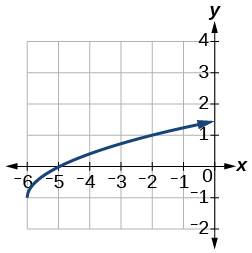
14)\(f(x)=\dfrac{1}{x+2}-1\)
Para los ejercicios 15-17, determinar si las funciones son pares, impares, o ninguna.
15)\(f(x)=-\dfrac{5}{x^{2}}+9 x^{6}\)
- Contestar
-
incluso
16)\(f(x)=-\dfrac{5}{x^{3}}+9 x^{5}\)
17)\(f(x)=\dfrac{1}{x}\)
- Contestar
-
impar
18) Graficar la función de valor absoluto\(f(x)=-2|x-1|+3\).
19) Resolver\(|2 x-3|=17\).
- Contestar
-
\(x=-7\)y\(x=10\)
20) Resolver\(-\left|\dfrac{1}{3} x-3\right| \geq 17\). Exprese la solución en notación de intervalos.
Para los ejercicios 21-22, encuentra la inversa de la función.
21)\(f(x)=3 x-5\)
- Contestar
-
\(f^{-1}(x)=\dfrac{x+5}{3}\)
22)\(f(x)=\dfrac{4}{x+7}\)
Para los ejercicios 23-26, utilice la gráfica de que\(g\) se muestra en la Figura a continuación.
23) ¿En qué intervalos aumenta la función?
- Contestar
-
\((-\infty,-1.1)\)y\((1.1, \infty)\)
24) ¿En qué intervalos disminuye la función?
25) Aproximar el mínimo local de la función. Exprese la respuesta como un par ordenado.
- Contestar
-
\((1.1,-0.9)\)
26) Aproximar el máximo local de la función. Exprese la respuesta como un par ordenado.
Para los ejercicios 27-29, utilice la gráfica de la función por tramos que se muestra en la Figura a continuación.
27) Encontrar\(f(2)\).
- Contestar
-
\(f(2)=2\)
28) Encontrar\(f(-2)\).
29) Escribir una ecuación para la función por partes.
- Contestar
-
\(f(x)=\left\{\begin{array}{cl}{|x|} & {\text { if } x \leq 2} \\ {3} & {\text { if } x>2}\end{array}\right.\)
Para los ejercicios 30-35, utilice los valores enumerados en la Tabla siguiente.
| \(x\) | \(F(x)\) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
| 6 | 13 |
| 7 | 15 |
| 8 | 17 |
30) Encontrar\(F(6)\).
31) Resolver la ecuación\(F(x)=5\)
- Contestar
-
\(x=2\)
32) ¿La gráfica está aumentando o disminuyendo en su dominio?
33) ¿La función está representada por la gráfica uno a uno?
- Contestar
-
si
34) Encontrar\(F^{-1}(15)\).
35) Dado\(f(x)=-2 x+11,\) hallazgo\(f^{-1}(x)\).
- Contestar
-
\(f^{-1}(x)=-\dfrac{x-11}{2}\)


