9.5: La Teoría Cinético-Molecular

habilidades para desarrollar

• Indicar los postulados de la Teoría Cinético-Molecular.
• Utilizar los postulados de esta teoría para explicar las leyes de los gases.

Las leyes de los gases que hemos visto hasta ahora, así como la ecuación de los gases ideales, son empíricas, es decir, se han derivado de observaciones experimentales. Las formas matemáticas de estas leyes describen el comportamiento macroscópico de la mayoría de los gases a presiones inferiores a 1 o 2 atm. Aunque las leyes de gases describen relaciones que han sido verificadas por muchos experimentos, no nos dicen por qué los gases siguen estas relaciones.

La teoría cinética molecular (KMT) es un modelo microscópico simple que explica efectivamente las leyes de gases descritas en módulos anteriores de este capítulo. Esta teoría se basa en los siguientes cinco postulados descritos aquí. (Nota: el término "molécula" se utilizará para referirse a las especies químicas individuales que componen el gas, aunque algunos gases están compuestos de especies atómicas, por ejemplo, los gases nobles).

1. Los gases están compuestos de moléculas que están en movimiento continuo, viajan en línea recta y cambian de dirección solo cuando chocan con otras moléculas o con las paredes de un recipiente.
2. Las moléculas que componen el gas son insignificantemente pequeñas en comparación con las distancias entre ellas.
3. La presión ejercida por un gas en un contenedor resulta de colisiones entre las moléculas de gas y las paredes del contenedor.
4. Las moléculas de gas no ejercen fuerzas atractivas o repulsivas entre sí o las paredes del recipiente; por lo tanto, sus colisiones son elásticas (no implican una pérdida de energía).
5. La energía cinética promedio de las moléculas de gas es proporcional a la temperatura de Kelvin del gas.

La prueba del KMT y sus postulados es su capacidad para explicar y describir el comportamiento de un gas. Las diversas leyes de gases se pueden derivar de los supuestos del KMT, que han llevado a los químicos a creer que los supuestos de la teoría representan con precisión las propiedades de las moléculas de gas. Primero veremos las leyes de gas individuales (Leyes de Boyle, Charles, Amontons, Avogadro y Dalton) conceptualmente para ver cómo el KMT las explica. Luego, consideraremos más cuidadosamente las relaciones entre las masas moleculares, las velocidades y las energías cinéticas con la temperatura, y explicaremos la Ley de Graham.

La teoría cinética-molecular explica el comportamiento de los gases, parte I

Recordando que la presión del gas se ejerce al mover rápidamente las moléculas de gas y depende directamente de la cantidad de moléculas que golpean un área unitaria de la pared por unidad de tiempo, vemos que el KMT explica conceptualmente el comportamiento de un gas de la siguiente manera:

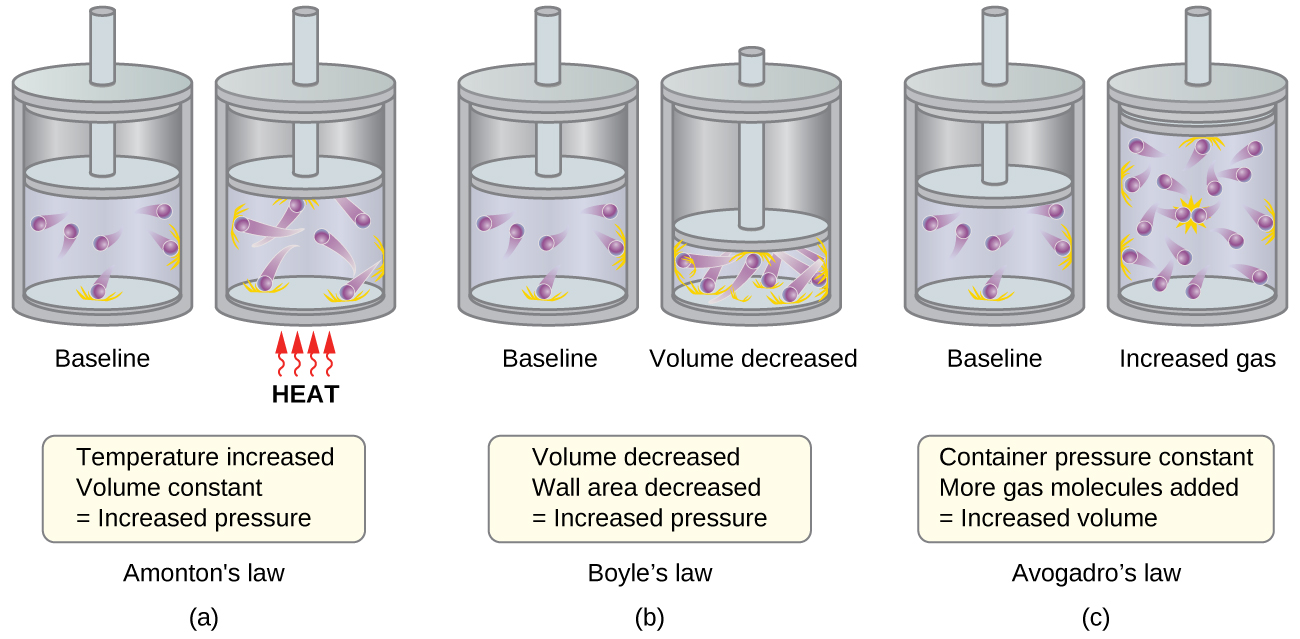
• La ley de Amonton. Si se aumenta la temperatura, aumentan la velocidad media y la energía cinética de las moléculas de gas. Si el volumen se mantiene constante, el aumento de la velocidad de las moléculas de gas resulta en colisiones más frecuentes y más contundentes con las paredes del recipiente, lo que aumenta la presión (Figura \(\PageIndex{1a}\)).
• La ley de Charles. Si aumenta la temperatura de un gas, se puede mantener una presión constante pero solo si aumenta el volumen ocupado por el gas. Esto dará como resultado mayores distancias promedio recorridas por las moléculas para llegar a las paredes del contenedor, así como un área de superficie de pared incrementada. Estas condiciones disminuirán tanto la frecuencia de las colisiones de la pared de la molécula como el número de colisiones por unidad de área, cuyos efectos combinados equilibran el efecto del aumento de las fuerzas de colisión debido a la mayor energía cinética a la temperatura más alta.
• Ley de Boyle. Si el volumen de gas disminuye, el área de la pared del recipiente disminuye y la frecuencia de colisión de la pared de la molécula aumenta, lo que aumenta la presión ejercida por el gas (Figura \(\PageIndex{1b}\)).
• Ley de Avogadro. A presión y temperatura constantes, la frecuencia y la fuerza de las colisiones de la pared de la molécula son constantes. En tales condiciones, aumentar el número de moléculas gaseosas requerirá un aumento proporcional en el volumen del contenedor para producir una disminución en el número de colisiones por unidad de área para compensar la mayor frecuencia de colisiones (Figura \(\PageIndex{1c}\)).
• Ley de Dalton. Debido a las grandes distancias entre ellas, las moléculas de un gas en una mezcla bombardean las paredes del recipiente con la misma frecuencia, ya sea que haya otros gases presentes o no, y la presión total de una mezcla de gases es igual a la suma de las presiones (parciales) de los gases individuales.

Figura \(\PageIndex{1}\): (a) Cuando la temperatura del gas aumenta, la presión del gas aumenta debido al aumento de la fuerza y la frecuencia de las colisiones moleculares. (b) Cuando el volumen disminuye, la presión del gas aumenta debido a la mayor frecuencia de colisiones moleculares. (c) Cuando la cantidad de gas aumenta a una presión constante, el volumen aumenta para producir un número constante de colisiones por unidad de área de pared por unidad de tiempo.

Las velocidades moleculares y la energía cinética

La discusión previa mostró que el KMT explica cualitativamente los comportamientos descritos por las diversas leyes de gases. Los postulados de esta teoría se pueden aplicar de manera más cuantitativa para derivar estas leyes individuales. Para hacer esto, primero debemos observar las velocidades y las energías cinéticas de las moléculas de gas, y la temperatura de una muestra de gas.

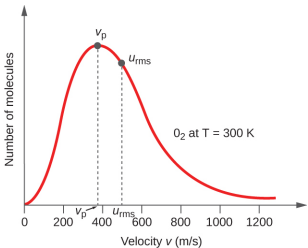
En una muestra de gas, las moléculas individuales tienen velocidades muy variables; sin embargo, debido a la gran cantidad de moléculas y colisiones involucradas, la distribución de la velocidad molecular y la velocidad promedio son constantes. Esta distribución de velocidad molecular se conoce como la distribución de Maxwell-Boltzmann, y representa el número relativo de moléculas en una muestra de volumen de gas que posee una velocidad dada (Figura \(\PageIndex{2}\)).

Figura \(\PageIndex{2}\): La distribución de la velocidad molecular para el gas oxígeno a 300 K se muestra aquí. Muy pocas moléculas se mueven a velocidades muy bajas o altas. El número de moléculas con velocidades intermedias aumenta rápidamente hasta un máximo, que es la velocidad más probable, luego disminuye rápidamente. Tenga en cuenta que la velocidad más probable, ν_p, es un poco menos de 400 m/s, mientras que la velocidad cuadrática media raíz, u_rms, está más cerca de 500 m/s.

La energía cinética (KE) de una partícula de masa (m) y velocidad (u) es dada por:

\[\ce{KE}=\dfrac{1}{2}mu^2\]

Expresando la masa en kilogramos y la velocidad en metros por segundo producirá valores de energía en unidades de julios (J = kg m² s ^{– 2}). Para lidiar con una gran cantidad de moléculas de gas, usamos promedios tanto para la velocidad como para la energía cinética. En el KMT, la velocidad cuadrática media de una partícula, u_rms, se define como la raíz cuadrada del promedio de los cuadrados de las velocidades con n = el número de partículas:

\[u_\ce{rms}=\sqrt{\overline{u^2}}=\sqrt{\dfrac{u^2_1+u^2_2+u^2_3+u^2_4+…}{n}}\]

La energía cinética promedio, KE_avg, es entonces igual a:

\[\mathrm{KE_{avg}}=\dfrac{1}{2}mu^2_\ce{rms}\]

El KE_avg de una colección de moléculas de gas también es directamente proporcional a la temperatura del gas y se puede describir mediante la ecuación:

\[\mathrm{KE_{avg}}=\dfrac{3}{2}RT\]

donde R es el constante de gas y T es la temperatura de Kelvin. Cuando se usa en esta ecuación, la forma apropiada del constante de gas es 8.314 J mol^-1K^-1 (8.314 kg m²s ^{– 2}mol^-1K ^{– 1}). Estas dos ecuaciones separadas para KE_avg se pueden combinar y reorganizar para producir una relación entre la velocidad molecular y la temperatura:

\[\dfrac{1}{2}mu^2_\ce{rms}=\dfrac{3}{2}RT\]

\[u_\ce{rms}=\sqrt{\dfrac{3RT}{m}} \label{RMS}\]

Ejemplo \(\PageIndex{1}\): Calculando de u_rms

Calculando la velocidad media cuadrática de una molécula de nitrógeno en 30 °C.

Solución

Convierta la temperatura en Kelvin:

\[30°C+273=303\: K\]

Determine la masa de una molécula de nitrógeno en kilogramos:

\[\mathrm{\dfrac{28.0\cancel{g}}{1\: mol}×\dfrac{1\: kg}{1000\cancel{g}}=0.028\:kg/mol}\]

Reemplace los variables y los constantes en la fórmula de velocidad cuadrática media (Ecuación \ref{RMS}), reemplazando Joules con el equivalente kg m²s^–2:

\[ \begin{align} u_\ce{rms} &= \sqrt{\dfrac{3RT}{m}} \\ u_\ce{rms} &=\sqrt{\dfrac{3(8.314\:J/mol\: K)(303\: K)}{(0.028\:kg/mol)}} \\ &=\sqrt{2.70 \times 10^5\:m^2s^{−2}} \\ &= 519\:m/s \end{align} \]

Ejercicio \(\PageIndex{1}\)

Calcule la velocidad cuadrática media de una molécula de oxígeno en –23 °C.

Respuesta

TBA

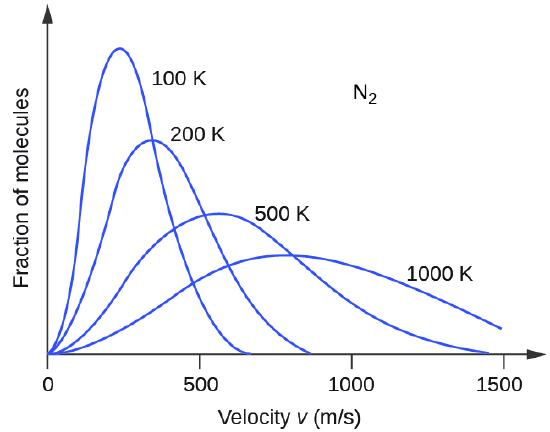
Si la temperatura de un gas aumenta, su KE_avg aumenta, más moléculas tienen velocidades más altas y menos moléculas tienen velocidades más bajas, y la distribución cambia hacia velocidades más altas en general, es decir, hacia la derecha. Si la temperatura disminuye, KE_avg disminuye, más moléculas tienen velocidades más bajas y menos moléculas tienen velocidades más altas, y la distribución cambia hacia velocidades más bajas en general, es decir, hacia la izquierda. Este comportamiento se ilustra para el gas nitrógeno en Figura \(\PageIndex{3}\).

Figura \(\PageIndex{3}\): La distribución de la velocidad molecular del gas nitrógeno (N₂) se desplaza hacia la derecha y se aplana cuando aumenta la temperatura; se desplaza hacia la izquierda y aumenta a medida que disminuye la temperatura.

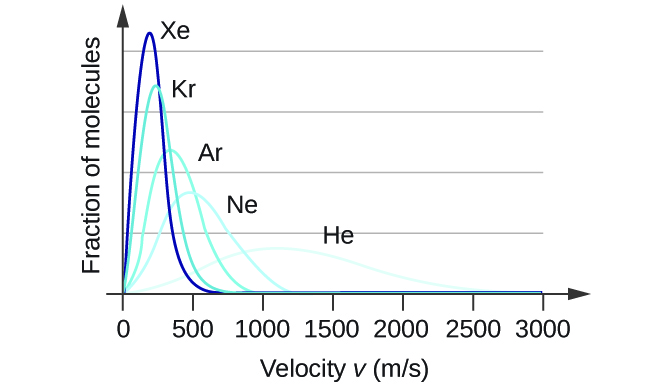
A una temperatura dada, todos los gases tienen el mismo KE_avg para sus moléculas. Los gases compuestos por moléculas más ligeras tienen más partículas de alta velocidad y u_rms más alta, con una distribución de velocidad que alcanza su punto máximo a velocidades relativamente más altas. Los gases que consisten en moléculas más pesadas tienen más partículas de baja velocidad, u_rms más bajos y una distribución de velocidad que alcanza su punto máximo a velocidades relativamente más bajas. Los datos de una serie de gases nobles que se muestran en la Figura \(\PageIndex{4}\) demuestran esta tendencia.

Figura \(\PageIndex{4}\): La velocidad molecular está directamente relacionada con la masa molecular. A una temperatura dada, las moléculas más ligeras se mueven más rápido en promedio que las moléculas más pesadas.

El simulador de gases se puede usar para examinar el efecto de la temperatura en las velocidades moleculares. Examine los "histogramas de energía" del simulador (distribuciones de velocidad molecular) y la "información de especies" (que da valores de velocidad promedio) para moléculas de diferentes masas a varias temperaturas.

La Teoría Cinética-Molecular explica el comportamiento de los gases, parte II

Según la Ley de Graham, las moléculas de un gas se mueven rápidamente y las moléculas son pequeñas. La distancia promedio entre las moléculas de un gas es grande en comparación con el tamaño de las moléculas. Como consecuencia, las moléculas de gas pueden pasar fácilmente entre sí y difundirse a velocidades relativamente rápidas.

La tasa de efusión de un gas depende directamente de la velocidad (promedio) de sus moléculas:

\[\textrm{effusion rate} ∝ u_\ce{rms}\]

Usando esta relación, y la ecuación que relaciona la velocidad molecular con la masa, la Ley de Graham se puede derivar fácilmente como se muestra aquí:

\[u_\ce{rms}=\sqrt{\dfrac{3RT}{m}}\]

\[m=\dfrac{3RT}{u^2_\ce{rms}}=\dfrac{3RT}{\overline{u}^2}\]

\[\mathrm{\dfrac{effusion\: rate\: A}{effusion\: rate\: B}}=\dfrac{u_\mathrm{rms\:A}}{u_\mathrm{rms\:B}}=\dfrac{\sqrt{\dfrac{3RT}{m_\ce{A}}}}{\sqrt{\dfrac{3RT}{m_\ce{B}}}}=\sqrt{\dfrac{m_\ce{B}}{m_\ce{A}}}\]

La relación de las tasas de efusión se deriva, por lo tanto, inversamente proporcional a la relación de las raíces cuadradas de sus masas. Esta es la misma relación observada experimentalmente y expresada como la ley de Graham.

Resumen

La teoría cinética molecular es un modelo simple pero muy efectivo que explica efectivamente el comportamiento ideal del gas. La teoría supone que los gases consisten en moléculas separadas de volumen insignificante que están en constante movimiento, chocando elásticamente entre sí y con las paredes de su recipiente con velocidades promedio determinadas por sus temperaturas absolutas. Las moléculas individuales de un gas exhiben un rango de velocidades, la distribución de estas velocidades depende de la temperatura del gas y la masa de sus moléculas.

Ecuaciones Clave

• \(u_\ce{rms}=\sqrt{\overline{u^2}}=\sqrt{\dfrac{u^2_1+u^2_2+u^2_3+u^2_4+…}{n}}\)
• \(\mathrm{KE_{avg}}=\dfrac{3}{2}RT\)
• \(u_\ce{rms}=\sqrt{\dfrac{3RT}{m}}\)

Glosario

teoría cinética molecular

teoría basada en principios simples y suposiciones que explican efectivamente el comportamiento ideal del gas

velocidad cuadrática media raíz (u_rms)

medida de la velocidad promedio para un grupo de partículas calculada como la raíz cuadrada de la velocidad cuadrada promedio

Contribuyentes

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

• Ana Martinez ([e-mail]) contribuyó a la traducción de este texto.