12.7: Los mecanismos de reacción

Última actualización
Guardar como PDF

Page ID: 1899

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

habilidades para desarrollar

Distinguir reacciones netas de reacciones elementales (los pasos)
Identificar la molecularidad de las reacciones elementales.
Escribir una ecuación química balanceada para un proceso dado el mecanismo de la reacción.
Derivar la ley de velocidad consistente con un mecanismo de reacción dado

Una ecuación balanceada para una reacción química indica lo que está reaccionando y lo que se produce, pero no revela nada acerca de cómo la reacción realmente toma lugar. El mecanismo de reacción (o el curso de la reacción) es el proceso por el cual ocurre una reacción. A veces, una reacción química ocurre por pasos, aunque no siempre es obvio para un observador. La descomposición del ozono, por ejemplo, parece seguir un mecanismo con dos pasos:

\[\ce{O3}(g)⟶\ce{O2}(g)+\ce{O}\\
\ce{O}+\ce{O3}(g)⟶\ce{2O2}(g) \label{12.7.1}\]

Llamamos cada paso en un mecanismo de reacción una reacción elemental. Las reacciones elementales ocurren exactamente como están escritas y no se pueden dividir en pasos más simples. Las reacciones elementales se suman a la reacción general, que, para la descomposición, es:

\[\ce{2O3}(g)⟶\ce{3O2}(g) \label{12.7.2}\]

Observe que el átomo de oxígeno producido en el primer paso de este mecanismo se consume en el segundo paso y, por lo tanto, no aparece como un producto en la reacción general. Las especies que se producen en un paso y se consumen en un paso posterior se llaman pasos intermedios.

Mientras la ecuación de reacción general para la descomposición del ozono indica que dos moléculas de ozono reaccionan para producir tres moléculas de oxígeno, el mecanismo de la reacción no implica la colisión y la reacción de dos moléculas de ozono. Más bien, involucra una molécula de ozono que se descompone en una molécula de oxígeno y un átomo de oxígeno intermedio; el átomo de oxígeno luego reacciona con una segunda molécula de ozono para producir dos moléculas de oxígeno. Estas dos reacciones elementales ocurren exactamente como se muestran en el mecanismo de la reacción.

Reacciones elementales unimoleculares

La molecularidad de una reacción elemental es el número de especies reactivas (átomos, moléculas o iones). Por ejemplo, una reacción unimolecular involucra la reorganización de una sola especie reactante para producir una o más moléculas de producto:

\[A⟶\ce{products} \label{12.7.2b}\]

La ecuación de velocidad para una reacción unimolecular es:

\[\ce{rate}=k[A] \label{12.7.3}\]

Una reacción unimolecular puede ser una de varias reacciones elementales en un mecanismo complejo. Por ejemplo, la reacción:

\[\ce{O3 ⟶ O2 + O} \label{12.7.4}\]

ilustra una reacción elemental unimolecular que ocurre como una parte de un mecanismo de reacción de dos pasos. Sin embargo, algunas reacciones unimoleculares pueden tener una sola reacción en el mecanismo de la reacción. (En otras palabras, una reacción elemental también puede ser una reacción general en algunos casos). Por ejemplo, la descomposición en fase gaseosa de ciclobutano, C₄H₈, a etileno, C₂H₄, se produce a través de un mecanismo unimolecular de un solo paso:

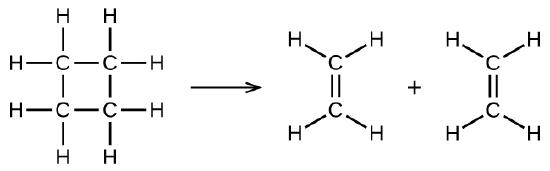
Para que ocurran estas reacciones unimoleculares, todo lo que se requiere es la separación de partes de moléculas reactivas individuales en productos.

Los enlaces químicos no se romperán simplemente durante las reacciones químicas. Se requiere energía para romper los enlaces químicos. La energía de activación para la descomposición de C₄H₈, por ejemplo, es de 261 kJ por mol. Esto significa que se requieren 261 kilojulios para distorsionar un mol de estas moléculas en complejos activados que se descomponen en productos:

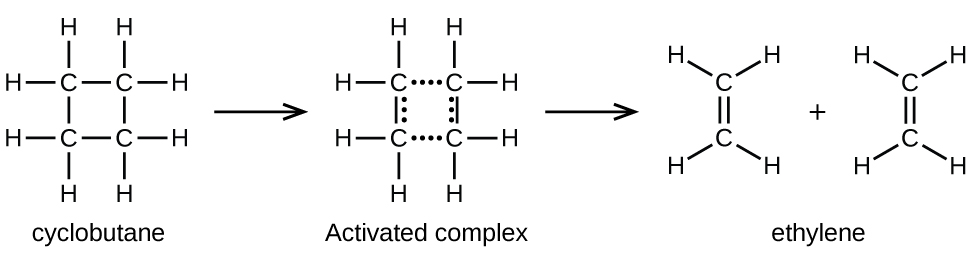
En una muestra de C₄H₈, algunas de las moléculas que se mueven rápidamente chocan con otras moléculas que se mueven rápidamente y recogen energía adicional. Cuando las moléculas de C₄H₈, obtienen suficiente energía, pueden transformarse en un complejo activado y se puede producir la formación de moléculas de etileno. En efecto, una colisión particularmente enérgica convierte una molécula de C₄H₈, en la geometría del complejo activado. Sin embargo, solo una pequeña fracción de las moléculas de gas viaja a velocidades suficientemente altas con energías cinéticas lo suficientemente grandes como para lograr esto. Por lo tanto, en cualquier momento dado, solo unas pocas moléculas recogen suficiente energía de las colisiones para reaccionar.

La velocidad de descomposición de C4H8 es directamente proporcional a su concentración. Duplicando la concentración de C4H8 en una muestra da el doble de moléculas por litro. Aunque la fracción de moléculas con suficiente energía para reaccionar sigue siendo la misma, el número total de tales moléculas es el doble. En consecuencia, hay el doble de C4H8 por litro, y la velocidad de reacción es dos veces más rápida:

\[\ce{rate}=−\dfrac{Δ[\ce{C4H8}]}{Δt}=k[\ce{C4H8}] \label{12.7.5}\]

Una relación similar se aplica a cualquier reacción elemental unimolecular; la velocidad de la reacción es directamente proporcional a la concentración del reactivo, y la reacción exhibe un comportamiento de primer orden. El constante de proporcionalidad es el constante de velocidad para la reacción unimolecular particular.

Reacciones elementales bimoleculares

La colisión y la combinación de dos moléculas o átomos para formar un complejo activado en una reacción elemental se llama una reacción bimolecular. Hay dos tipos de reacciones elementales bimoleculares:

\[A+B⟶\ce{products} \label{12.7.6}\]

\[2A⟶\ce{products} \label{12.7.7}\]

Para el primer tipo, en el que las dos moléculas reactivas son diferentes, la ley de velocidad es de primer orden en A y de primer orden en B:

\[\ce{rate}=k[A][B] \label{12.7.8}\]

Para el segundo tipo, en el cual las dos moléculas idénticas chocan y reaccionan, la ley de velocidad es de segundo orden en A:

\[\ce{rate}=k[A][A]=k[A]^2 \label{12.7.9}\]

Algunas reacciones químicas tienen mecanismos que consisten en una única reacción elemental bimolecular. Un ejemplo es la reacción de dióxido de nitrógeno con el monóxido de carbono:

\[\ce{NO2}(g)+\ce{CO}(g)⟶\ce{NO}(g)+\ce{CO2}(g) \label{12.7.10}\]

(vea Figura \(\PageIndex{1}\))

This figure provides an illustration of a reaction between two H I molecules using space filling models. H atoms are shown as white spheres, and I atoms are shown as purple spheres. On the left, two H I molecules are shownwith a small white sphere bonded to a much larger purple sphere. The label, “Two H I molecules,” appears below. An arrow points right to a similar structure in which the two molecules appear pushed together, so that the purple spheres of the two molecules are touching. Below appears the label, “Transition state.” Following another arrow, two white spheres are shown vertically oriented and bonded together with the label, “H subscript 2” above. The H subscript 2 molecule is followed by a plus sign and two purple spheres bonded together with the label, “I subscript 2” above. Below these structures is the label, “Hydrogen iodide molecules decompose to produce hydrogen H subscript 2 and iodine I subscript 2.” — Figura \(\PageIndex{1}\): El mecanismo probable para la reacción entre\(\ce{NO_2}\) y \(\ce{CO}\) para producir \(\ce{NO}\) y \(\ce{CO_2}\).

Las reacciones elementales bimoleculares también pueden estar involucradas como pasos en un mecanismo de reacción de varios pasos. La reacción del oxígeno atómico con el ozono es un ejemplo:

\[\ce{O}(g)+\ce{O3}(g)⟶\ce{2O2}(g) \label{12.7.12}\]

Reacciones elementales termoleculares

Una reacción termolecular elemental involucra la colisión simultánea de tres átomos, moléculas o iones. Las reacciones elementales termoleculares no son frecuentes porque la probabilidad de que tres partículas colisionen simultáneamente es menor que una milésima parte de la probabilidad de que dos partículas colisionen. Sin embargo, hay algunas reacciones elementales termoleculares establecidas. La reacción del óxido nítrico con el oxígeno parece involucra pasos termoleculares:

\[\ce{2NO + O2 ⟶ 2NO2}\\
\ce{rate}=k[\ce{NO}]^2[\ce{O2}] \label{12.7.13}\]

Asimismo, la reacción del óxido nítrico con el cloro parece involucrar pasos termoleculares:

\[\ce{2NO + Cl2 ⟶ 2NOCl}\\
\ce{rate}=k[\ce{NO}]^2[\ce{Cl2}] \label{12.7.14}\]

Relating Reaction Mechanisms to Rate Laws

A veces ocurre que un paso en un mecanismo de reacción de varios pasos es significativamente más lento que los otros. Debido a que una reacción no puede avanzar más rápido que su paso más lento, este paso limitará la velocidad a la que ocurre la reacción general. Por lo tanto, el paso más lento se llama el paso limitante de la velocidad (o el paso determinante de la velocidad) de la Figura de reacción \(\PageIndex{2}\).

A photo is shown of cattle passing through a narrow chute into a holding pen. A person directs them through the gate with a long white and red pole. — Figura \(\PageIndex{2}\): Una tolva de ganado es un ejemplo que no involucra la química pero involucra un paso determinante de la velocidad. El ganado solo se puede mover de un corral de retención a otro tan rápido como un animal puede atravesar la rampa. (crédito: Loren Kerns)

Como se describió anteriormente, las leyes de velocidad se pueden derivar directamente de las ecuaciones químicas para reacciones elementales. Sin embargo, este no es el caso para las reacciones químicas ordinarias. Las ecuaciones balanceadas más frecuentemente estudiadas representan el cambio general para algún sistema químico, y muy a menudo es el resultado de algunos mecanismos de reacción de varios pasos. En todos los casos, debemos determinar la ley de tasa general a partir de los datos experimentales y deducir el mecanismo de la ley de tasa (y a veces de otros datos). La reacción de NO₂ y CO nos da un ejemplo ilustrativo:

\[\ce{NO2}(g)+\ce{CO}(g)⟶\ce{CO2}(g)+\ce{NO}(g)\]

Para las temperaturas más altas de 225 °C, se ha encontrado que la ley de velocidad es:

\[\ce{rate}=k[\ce{NO2}][\ce{CO}]\]

La reacción es de primer orden con respecto al NO₂ y de primer orden con respecto al CO. Esto es consistente con un mecanismo bimolecular de un solo paso y es posible que este sea el mecanismo para esta reacción a altas temperaturas.

A temperaturas más bajas de 225 °C, la reacción se describe usando una ley de velocidad de segundo orden con respecto al NO₂:

\[\ce{rate}=k[\ce{NO2}]^2\]

Esto es consistente con un mecanismo que involucra las siguientes dos reacciones elementales, la primera de las cuales es más lenta y, por lo tanto, es el paso determinante de la velocidad de la reacción:

\[\ce{NO2}(g)+\ce{NO2}(g)⟶\ce{NO3}(g)+\ce{NO}(g)\:\ce{(slow)}\\
\ce{NO3}(g)+\ce{CO}(g)⟶\ce{NO2}(g)+\ce{CO2}(g)\:\ce{(fast)}\]

El paso de determinación de la velocidad nos da una ley de velocidad que muestra una dependencia de segundo orden de la concentración de NO₂, y la suma de las dos ecuaciones da la reacción global neta.

En general, cuando el paso de determinación de velocidad (más lento) es el primer paso en un mecanismo, la ley de velocidad para la reacción general es la misma que la ley de velocidad para este paso. Sin embargo, cuando el paso de determinación de la velocidad está precedido por un paso que involucra una reacción de equilibrio, la ley de la velocidad de la reacción general puede ser más difícil de derivar.

Una reacción elemental está balanceada cuando procede tanto en dirección hacia adelante como hacia atrás a velocidades iguales. Considere la dimerización de NO a N₂O₂, con k₁ usado para representar el constante de velocidad de la reacción directa y k-1 usado para representar el constante de velocidad de la reacción inversa:

\[\ce{NO + NO ⇌ N2O2}\]

\[\ce{rate_{forward}=rate_{reverse}}\]

\[k_1[\ce{NO}]^2=k_{−1}[\ce{N2O2}]\]

Si N₂O₂ fuera un intermediario en un mecanismo, esta expresión se podría reorganizar para representar la concentración de N₂O₂ en la expresión de la ley de velocidad general usando la manipulación algebraica:

\[\mathrm{\left(\dfrac{k_1[NO]^2}{k_{−1}}\right)=[N_2O_2]}\]

Sin embargo, una vez más, los intermedios no se pueden considerar como parte de la expresión general de la ley de tasas, aunque se pueden incluir en una reacción elemental individual de un mecanismo. El ejemplo \(\PageIndex{1}\) ilustrará cómo derivar las leyes generales de la tasa a partir de mecanismos que involucran pasos de equilibrio que preceden al paso de determinación de la tasa.

Ejemplo \(\PageIndex{1}\): DERIVANDO LA EXPRESIÓN GENERAL DE LA LEY DE TASAS PARA UNA REACCIÓN CON VARIOS PASOS

Mecanismo: El cloruro de nitrilo (NO₂Cl) se descompone al dióxido de nitrógeno (NO₂) y el gas de cloro (Cl₂) de acuerdo con el siguiente mecanismo:

\(\ce{2NO2Cl}(g)⇌\ce{ClO2}(g)+\ce{N2O}(g)+\ce{ClO}(g)\) (rápido, k₁ representa el constante de velocidad para la reacción directa y k−1 el constante de velocidad para la reacción inversa)
\(\ce{N2O}(g)+\ce{ClO2}(g)⇌\ce{NO2}(g)+\ce{NOCl}(g)\) (rápido, k₂ para la reacción directa, k−2 para la reacción inversa)
\(\ce{NOCl + ClO ⟶ NO2 + Cl2}\) (despacio, k₃ la velocidad del constante para la reacción directa)

Determine la reacción general, escriba la expresión de la ley de velocidad para cada reacción elemental, identifique los intermedios y determine la expresión de la ley de velocidad general.

Solución

Para la reacción general, simplemente sume los tres pasos, cancele los intermedios y combine las fórmulas similares:

\[\ce{2NO2Cl}(g)⟶\ce{2NO2}(g)+\ce{Cl2}(g) \nonumber\]

Luego, escriba la expresión de la ley de velocidad para cada reacción elemental. Recuerde que para las reacciones elementales que forman parte de un mecanismo, la expresión de la ley de velocidad puede derivarse directamente de la estequiometría:

\[\begin{align*}
k_1\ce{[NO2Cl]2}&=k_{−1}\ce{[ClO2][N2O][ClO]}\\
k_2\ce{[N2O][ClO2]}&=k_{−2}\ce{[NO2][NOCl]}\\
\ce{Rate}&=k_3\ce{[NOCl][ClO]}
\end{align*}\]

El tercer paso, que es el paso despacio, es el paso que determina la velocidad de la reacción. Por lo tanto, la expresión de la ley de velocidad general se podría escribir como Velocidad = k₃ [NOCl][ClO]. Sin embargo, tanto NOCl como ClO son intermedios. Las expresiones algebraicas se deben usar para representar [NOCl] y [ClO] de modo que no queden intermedios en la expresión de la ley de velocidad general.

Usando reacción elemental 1, \(\ce{[ClO]}=\dfrac{k_1\ce{[NO2Cl]^2}}{k_{−1}\ce{[ClO2][N2O]}}\).
Usando reacción elemental 2, \(\ce{[NOCl]}=\dfrac{k_2\ce{[N2O][ClO2]}}{k_{−2}\ce{[NO2]}}\).

Ahora sustituya estas expresiones algebraicas en la expresión de la ley de velocidad general y simplifique:

\[\begin{align*}
\ce{rate}&=k_3\left(\dfrac{k_2\ce{[N2O][ClO2]}}{k_{−2}\ce{[NO2]}}\right)\left(\dfrac{k_1\ce{[NO2Cl]^2}}{k_{−1}\ce{[ClO2][N2O]}}\right)\\
\ce{rate}&=\dfrac{k_3k_2k_1\ce{[NO2Cl]^2}}{k_{−2}k_{−1}\ce{[NO2]}}
\end{align*}\]

Observe que esta ley de velocidad muestra una dependencia inversa de la concentración de una de las especies del producto, consistente con la presencia de un paso de equilibrio en el mecanismo de la reacción.

Ejercicio \(\PageIndex{1}\)

El cloro atómico en la atmósfera reacciona con el ozono en el siguiente par de reacciones elementales:

\(\ce{Cl}+\ce{O3}(g)⟶\ce{ClO}(g)+\ce{O2}(g)\hspace{20px}(\textrm{rate constant }k_1)\)

\(\ce{ClO}(g)+\ce{O}⟶\ce{Cl}(g)+\ce{O2}(g)\hspace{20px}(\textrm{rate constant }k_2)\)

Determine la reacción general, escriba la expresión de la ley de velocidad para cada reacción elemental, identifique los intermedios y determine la expresión de la ley de velocidad general.

Respuesta:

reacción general: \(\ce{O3}(g)+\ce{O}⟶\ce{2O2}(g)\)
_velocidad1 = k₁[O₃][Cl]; rate₂ = k₂[ClO][O]
intermedio: ClO(g)
reacción general= k₂k₁[O₃][Cl][O]

Resumen

La secuencia de pasos individuales, o reacciones elementales, por las cuales los reactivos se convierten en productos durante el curso de una reacción se llama el mecanismo de la reacción. La velocidad general de una reacción está determinada por la velocidad del paso más lento, llamado el paso determinante de la velocidad. Las reacciones elementales unimoleculares tienen leyes de tasa de primer orden, mientras que las reacciones elementales bimoleculares tienen leyes de tasa de segundo orden. Al comparar las leyes de velocidad derivadas de un mecanismo de reacción con el determinado experimentalmente, el mecanismo se puede considerar incorrecto o plausible.

Notas al pie de la página

Esta pregunta está tomada del Examen de Colocación Avanzada de Química y se usa con el permiso del Servicio de Pruebas Educativas.

Glosario

reacción bimolecular: reacción elemental que implica la colisión y la combinación de dos especies reactivas

reacción elemental: reacción que tiene lugar precisamente como se describe en su ecuación química

intermedio: molécula o ion producido en un paso de un mecanismo de reacción y consumido en otro paso

molecularidad: Número de especies reactivas (átomos, moléculas o iones) involucradas en una reacción elemental

paso determinante de la velocidad: (también, paso de limitación de velocidad) la reacción elemental más lenta en un mecanismo de reacción; determina la velocidad de la reacción general

mecanismo de la reacción: secuencia gradual de las reacciones elementales por las cuales se produce un cambio químico

reacción termolecular: reacción elemental que implica la colisión simultánea y la combinación de tres especies reactivas

reacción unimolecular: reacción elemental que involucra la reorganización de una sola especie reactante para producir una o más moléculas de producto

Contribuyentes

Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.

Search

Text Color

Text Size

Margin Size

Font Type

Contribuyentes