1.1: Relaciones empíricas y características específicas de los métodos de cálculo utilizados para resolver problemas cinéticos no isotérmicos

La resolución del problema cinético consiste en varios pasos. En el primer paso se resuelve el problema cinético inverso evaluando los parámetros de Arrhenius. Sin embargo, la solución requiere una serie de experimentos con diferentes velocidades de calentamiento y determinación de condiciones experimentales óptimas:

\[\ce{A_{s} -> B_{s} + C_{g}} \label{1.1}\]

donde A _s es el reactivo sólido en polvo inicial que forma una capa plana, B _s es el producto de reacción sólido localizado en los granos del reactivo inicial, y C _g es el producto de reacción gaseoso liberado al ambiente. Este proceso se denomina cuasi-una etapa, por lo que las reacciones del tipo de Ecuación\ ref {1.1} tienen al menos tres etapas y comprenden la etapa de reacción química, transferencia de calor y masa. Sin embargo, dependiendo de las condiciones experimentales, una de las etapas puede ser limitante. En nuestro caso, creemos que la reacción química es la etapa limitante de velocidad. Supongamos que la dependencia de este proceso en el tiempo y la temperatura es una curva termoanalítica monomodo.

Para tal proceso, el cambio en la velocidad de reacción en función de la temperatura se puede describir de la siguiente manera:

\[-\frac{d \alpha}{d t}=A e^{\frac{-E}{R T}} f(\alpha) \label{1.2}\]

donde A y E son los parámetros de Arrhenius, T es la temperatura y f (α) es alguna función de la conversión de la reacción que caracteriza su mecanismo.

La conversión\(\alpha\), de acuerdo con la Ecuación\ ref {1.1}, se define como la fracción del reactivo inicial A _s que ha reaccionado en el tiempo t _i y cambia de 0 a 1. Vale la pena señalar que la conversión\(\alpha\) puede calcularse tanto a partir de los datos TG como DSC, así como a partir de los datos de termogravimetría diferencial (DTG).

Las llamadas técnicas cinéticas no isotérmicas son ampliamente utilizadas debido a la aparente simplicidad del procesamiento de datos experimentales de acuerdo con el modelo cinético formal descrito por la Ecuación\ ref {1.2}. La ecuación\ ref {1.2} caracteriza una sola curva de medición.

Aplicado a los datos experimentales de TA, el modelo cinético se puede representar en la siguiente forma:

\[-\frac{\mathrm{d} \alpha}{\mathrm{d} T_{T=T_{i}}}=\frac{A}{\beta_{i}} \exp \left(-\frac{E}{R T}\right) \alpha_{i}^{m}\left(1-\alpha_{i}\right)^{n} \label{1.3}\]

donde (1 - α _i) es el grado de incompletitud de reacción medido experimentalmente, T _i es la temperatura actual en kelvin (K),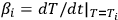 es la velocidad de calentamiento instantánea (en nuestro experimento, β _i = β = constante), А es el factor preexponencial, E es la energía de activación, m y n son el parámetro de la ecuación cinética [1].

La ecuación\ ref {1.3} se linealiza fácilmente:

\[\ln \left(-\frac{\mathrm{d} \alpha}{\mathrm{d} T}_{T=T_{i}}\right)=\ln \left(\frac{A}{\beta_{i}}\right)-\frac{E}{R T_{i}}+m \cdot \ln \alpha_{i}+n \cdot \ln \left(1-\alpha_{i}\right) \label{1.4}\]

es decir, se reduce a un problema lineal de mínimos cuadrados.

El problema de mínimos cuadrados para la Ecuación\ ref {1.4} se reduce a resolver el siguiente conjunto de ecuaciones:

\[C \vec{x}=\vec{b} \label{1.5}\]

donde C es la matriz de coeficientes de la Ecuación\ ref {1.4} (C _i1 = 1/β _i, C _i2 = -1/ T _i, C _i3 = lnα _i, C _i4 = ln (1-α)), y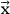 es el vector de los parámetros buscados. Dado que los datos experimentales son números aleatorios, se determinan con cierto error.

Resolver el problema en la Ecuación\ ref {1.5} implica ciertas dificultades.

El valor 1/ T cambia de manera insignificante en el rango de temperatura de reacción, por lo tanto, la primera y segunda columna de la matriz C son prácticamente idénticas (hasta un multiplicador constante), y como resultado la matriz С es casi degenerada. Descripción detallada de este problema se puede encontrar en. Para minimizar la incertidumbre se deben proporcionar varios experimentos con diferentes velocidades de calentamiento y calcular los parámetros cinéticos utilizando todos los datos experimentales.

Los argumentos anteriores sugieren únicamente que el cálculo de los parámetros de Arrhenius utilizando una sola curva termoanalítica es incorrecto. El software Netzsch Termokinetics utiliza un enfoque diferente, cuando los parámetros de Arrhenius se estiman utilizando métodos de cálculo sin modelo de acuerdo con una serie de experimentos a diferentes velocidades de calentamiento (ver abajo).

El problema cinético inverso así resuelto no garantiza la adecuada descripción de los datos experimentales. Para verificar la adecuación de la solución, es necesario resolver el problema directo, es decir, integrar la Ecuación\ ref {1.3} y comparar las dependencias calculadas y experimentales en todo el rango de velocidades de calentamiento. Este procedimiento ha sido implementado en los paquetes del programa de Termocinética, Separación de Picos y Simulación Térmica de NETZSCH con la ayuda de NETZSCH. Estos programas y sus aplicaciones se discuten en detalle a continuación.

El procesamiento conjunto de los resultados experimentales obtenidos a diferentes velocidades de calentamiento requiere la constancia del mecanismo de un proceso, es decir, la constancia del tipo de función f (α) a diferentes velocidades de calentamiento. Si se cumple esta condición se puede verificar mediante transformación afín de curvas experimentales, es decir, mediante el uso de coordenadas reducidas. Para ello, se deben seleccionar variables sobre la abscisa y la ordenada para que cada una de ellas cambie independientemente del proceso que se esté considerando. Además, es deseable que la relación entre las variables seleccionadas y los valores experimentales sea simple. Estos requisitos se cumplen con coordenadas reducidas. Una cantidad reducida se define como la relación de alguna cantidad experimental variable con respecto a otra cantidad experimental de la misma naturaleza. Como una de las variables, se utiliza la conversión α, la cual se define como la fracción de la cantidad inicial del reactivo que se ha convertido en un momento dado de tiempo. En cinética heterogénea, esta variable es, por regla general, la conversión del reactivo sólido inicial.

Si es necesario reflejar la relación entre la conversión y el tiempo o la temperatura en el experimento termoanalítico (a diversas velocidades de calentamiento), entonces se usa el α como ordenada y la cantidad reducida igual a la relación del tiempo actual t o temperatura T correspondiente a este tiempo al tiempo t _{α *} que se necesita para lograr la conversión deseada. Por ejemplo, si se selecciona el tiempo o temperatura requerida para lograr 50 o 90% de conversión (α * = 0.5 o 0.9), las cantidades reducidas serán t/t _0.5 (T/T _0.5) o t/t _0.9 (T/T _0.9).

El formalismo anterior se refiere a la etapa química de un proceso heterogéneo [4,5]. Sin embargo, se debe tomar en cuenta que en general el proceso heterogéneo puede implicar transferencia de calor y masa, es decir, el proceso puede ser nunca estrictamente de un solo paso. El carácter multietapa de un proceso complica significativamente la solución del problema cinético. En este caso, se debe resolver un conjunto de al menos tres ecuaciones diferenciales con derivadas parciales, lo que a menudo hace que el problema sea irresoluble. Al mismo tiempo, se pueden encontrar condiciones experimentales bajo las cuales una de las etapas, con mayor frecuencia, la etapa química, sería la etapa limitante de velocidad del proceso. Tales condiciones experimentales se encuentran en un experimento cinético especial.