11.7: Electrólisis

Objetivos de aprendizaje

• Comprender la electrólisis y describirla cuantitativamente.

En este capítulo, hemos descrito diversas celdas galvánicas en las que se utiliza una reacción química espontánea para generar energía eléctrica. En una celda electrolítica, sin embargo, ocurre el proceso opuesto, llamado electrólisis: se aplica un voltaje externo para impulsar una reacción no espontánea. En esta sección, analizamos cómo se construyen las celdas electrolíticas y exploramos algunas de sus muchas aplicaciones comerciales.

Celdas electrolíticas

Si construimos una celda electroquímica en la que un electrodo es cobre metálico sumergido en una solución 1 M Cu ^{2 +} y el otro electrodo es metal cadmio sumergido en una\(\,1\; M\, Cd^{2+}\) solución y luego cerramos el circuito, la diferencia de potencial entre los dos compartimentos será de 0.74 V. El electrodo de cadmio comenzará a disolverse (Cd se oxida a Cd ^{2 +}) y es el ánodo, mientras que el cobre metálico se depositará sobre el electrodo de cobre (Cu ^{2 +} se reduce a Cu), que es el cátodo (Figura\(\PageIndex{1a}\)).

Figura\(\PageIndex{1}\): Un voltaje aplicado puede revertir el flujo de electrones en una celda galvánica de Cd/Cu. (a) Cuando los compartimentos que contienen un electrodo de Cd sumergido en 1 M Cd ^{2 +} (aq) y un electrodo de Cu sumergido en 1 M Cu ^{2 +} (aq) se conectan para crear una celda galvánica, Cd (s) se oxida espontáneamente a Cd ^{2 +} (aq) en el ánodo, y Cu ^{2 +} (aq) se reduce espontáneamente a Cu (s) en el cátodo. El potencial de la celda galvánica es de 0.74 V. (b) La aplicación de un potencial externo mayor a 0.74 V en la dirección inversa obliga a los electrones a fluir desde el electrodo de Cu [que ahora es el ánodo, en el que Cu (s) metálico se oxida a Cu ^{2 +} (aq)] y al electrodo de Cd [que es ahora el cátodo, en el que Cd ^{2 +} (aq) se reduce a Cd (s)]. El ánodo en una celda electrolítica es positivo porque los electrones están fluyendo de ella, mientras que el cátodo es negativo porque los electrones están fluyendo hacia él. (CC BY-SA-NC; anónimo)

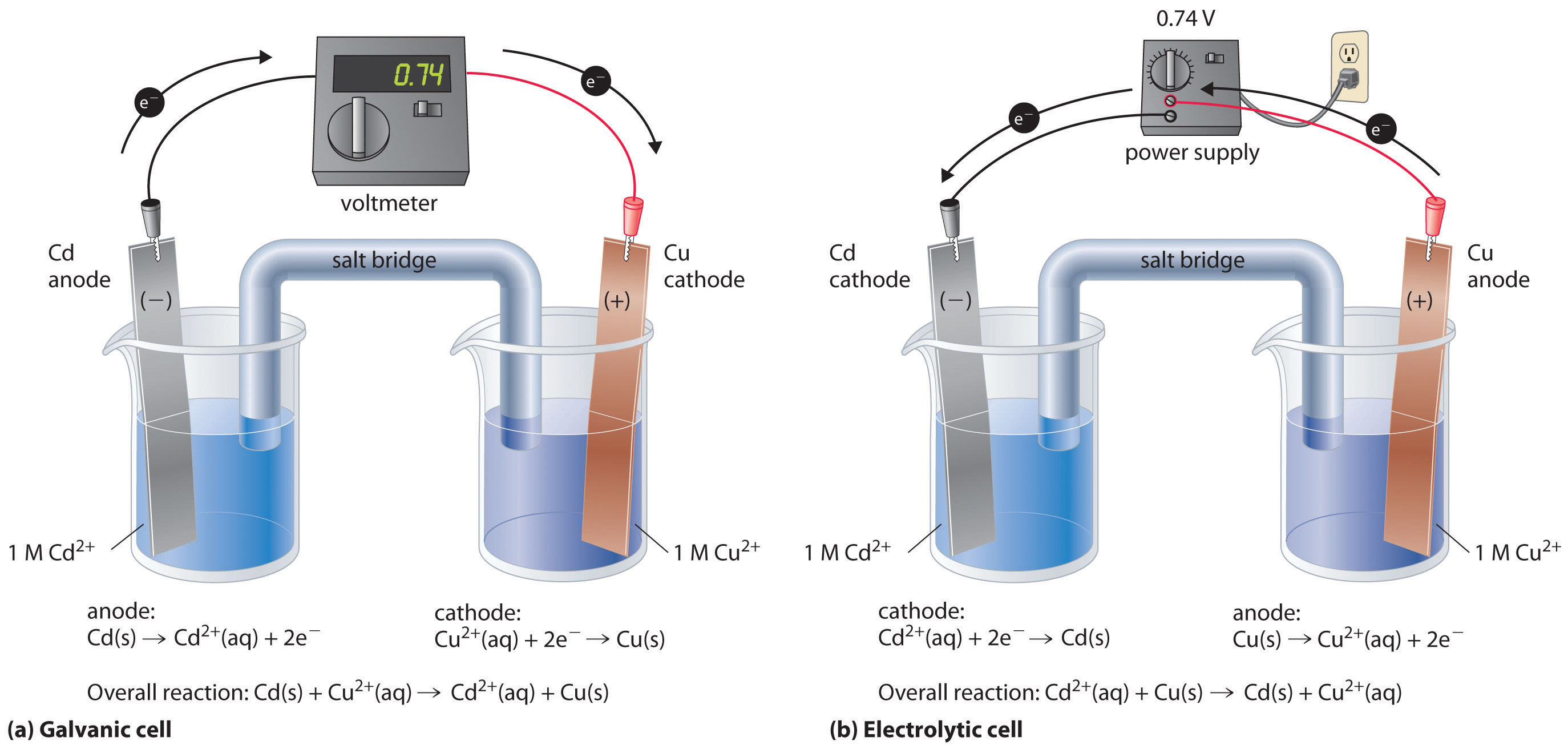
La reacción global es la siguiente:

\[ \ce{Cd (s) + Cu^{2+} (aq) \rightarrow Cd^{2+} (aq) + Cu (s)} \nonumber \]

con\(E°_{cell} = 0.74\; V\)

Esta reacción es termodinámicamente espontánea como escrito (\(ΔG^o < 0\)):

\[ \begin{align*} \Delta G^\circ &=-nFE^\circ_\textrm{cell} \\[4pt] &=-(\textrm{2 mol e}^-)[\mathrm{96,485\;J/(V\cdot mol)}](\mathrm{0.74\;V}) \\[4pt] &=-\textrm{140 kJ (per mole Cd)} \end{align*} \nonumber \]

En esta dirección, el sistema está actuando como una celda galvánica.

En una celda electrolítica, se aplica un voltaje externo para impulsar una reacción no espontánea.

La reacción inversa, la reducción de Cd ^{2 +} por Cu, es termodinámicamente no espontánea y ocurrirá solo con una entrada de 140 kJ. Podemos forzar que la reacción continúe en sentido inverso aplicando un potencial eléctrico mayor a 0.74 V desde una fuente de alimentación externa. El voltaje aplicado fuerza a los electrones a través del circuito en la dirección inversa, convirtiendo una celda galvánica en una celda electrolítica. Así el electrodo de cobre es ahora el ánodo (Cu está oxidado), y el electrodo de cadmio ahora es el cátodo (Cd ^{2 +} se reduce) (Figura\(\PageIndex{1b}\)). Los signos del cátodo y el ánodo se han conmutado para reflejar el flujo de electrones en el circuito. Las medias reacciones que ocurren en el cátodo y el ánodo son las siguientes:

• media reacción en el cátodo:

\[\ce{Cd^{2+}(aq) + 2e^{−} \rightarrow Cd(s)}\label{20.9.3} \]

con\(E^°_{cathode} = −0.40 \, V\)

• media reacción en el ánodo:

\[\ce{Cu(s) \rightarrow Cu^{2+}(aq) + 2e^{−}} \label{20.9.4} \]

con\(E^°_{anode} = 0.34 \, V \)

• Reacción general:

\[\ce{Cd^{2+}(aq) + Cu(s) \rightarrow Cd(s) + Cu^{2+}(aq) } \label{20.9.5} \]

con\(E^°_{cell} = −0.74 \: V\)

Porque\(E^°_{cell} < 0\), la reacción general, la reducción de\(Cd^{2+}\) por\(Cu\), claramente no puede ocurrir espontáneamente y solo procede cuando se aplica suficiente energía eléctrica. Las diferencias entre celdas galvánicas y electrolíticas se resumen en la Tabla\(\PageIndex{1}\).

Tabla\(\PageIndex{1}\): Comparación de celdas galvánicas y electrolíticas

Inmueble	Celda Galvánica	Celda electrolítica
ΔG	< 0	> 0
Celda E	> 0	< 0
Proceso de Electrodos
ánodo	oxidación	oxidación
cátodo	reducción	reducción
Signo de Electrodo
ánodo	−	+
cátodo	+	−

Reacciones electrolíticas

A temperaturas suficientemente altas, los sólidos iónicos se funden para formar líquidos que conducen la electricidad extremadamente bien debido a las altas concentraciones de iones. Si se insertan dos electrodos inertes en fundido\(\ce{NaCl}\), por ejemplo, y se aplica un potencial eléctrico,\(\ce{Cl^{-}}\) se oxida en el ánodo y\(\ce{Na^{+}}\) se reduce en el cátodo. La reacción global es la siguiente:

\[\ce{ 2NaCl (l) \rightarrow 2Na(l) + Cl2(g)} \label{20.9.6} \]

Esto es lo contrario de la formación de\(\ce{NaCl}\) a partir de sus elementos. El producto de la reacción de reducción es sodio líquido debido a que el punto de fusión del sodio metálico es 97.8°C, muy por debajo del de\(\ce{NaCl}\) (801°C). Aproximadamente 20,000 toneladas de metal de sodio se producen comercialmente en Estados Unidos cada año por la electrólisis del fundido\(\ce{NaCl}\) en una celda Downs (Figura\(\PageIndex{2}\)). En esta celda especializada, primero se agrega\(\ce{CaCl2}\) (punto de fusión = 772°C)\(\ce{NaCl}\) a la para disminuir el punto de fusión de la mezcla a aproximadamente 600°C, disminuyendo así los costos de operación.

Figura\(\PageIndex{2}\): Una Celda Downs para la Electrólisis de NaCl Fundido. La electrólisis de una mezcla fundida de NaCl y CaCl ₂ da como resultado la formación de gas elemental de sodio y cloro. Debido a que el sodio es un líquido en estas condiciones y el sodio líquido es menos denso que el cloruro de sodio fundido, el sodio flota hasta la parte superior de la masa fundida y se recoge en cilindros de hierro concéntricos tapados que rodean el cátodo. El cloro gaseoso se acumula en el cono invertido sobre el ánodo. Una pantalla de hierro que separa los compartimentos de cátodo y ánodo asegura que el sodio fundido y el cloro gaseoso no entren en contacto. (CC BY-SA-NC; anónimo)

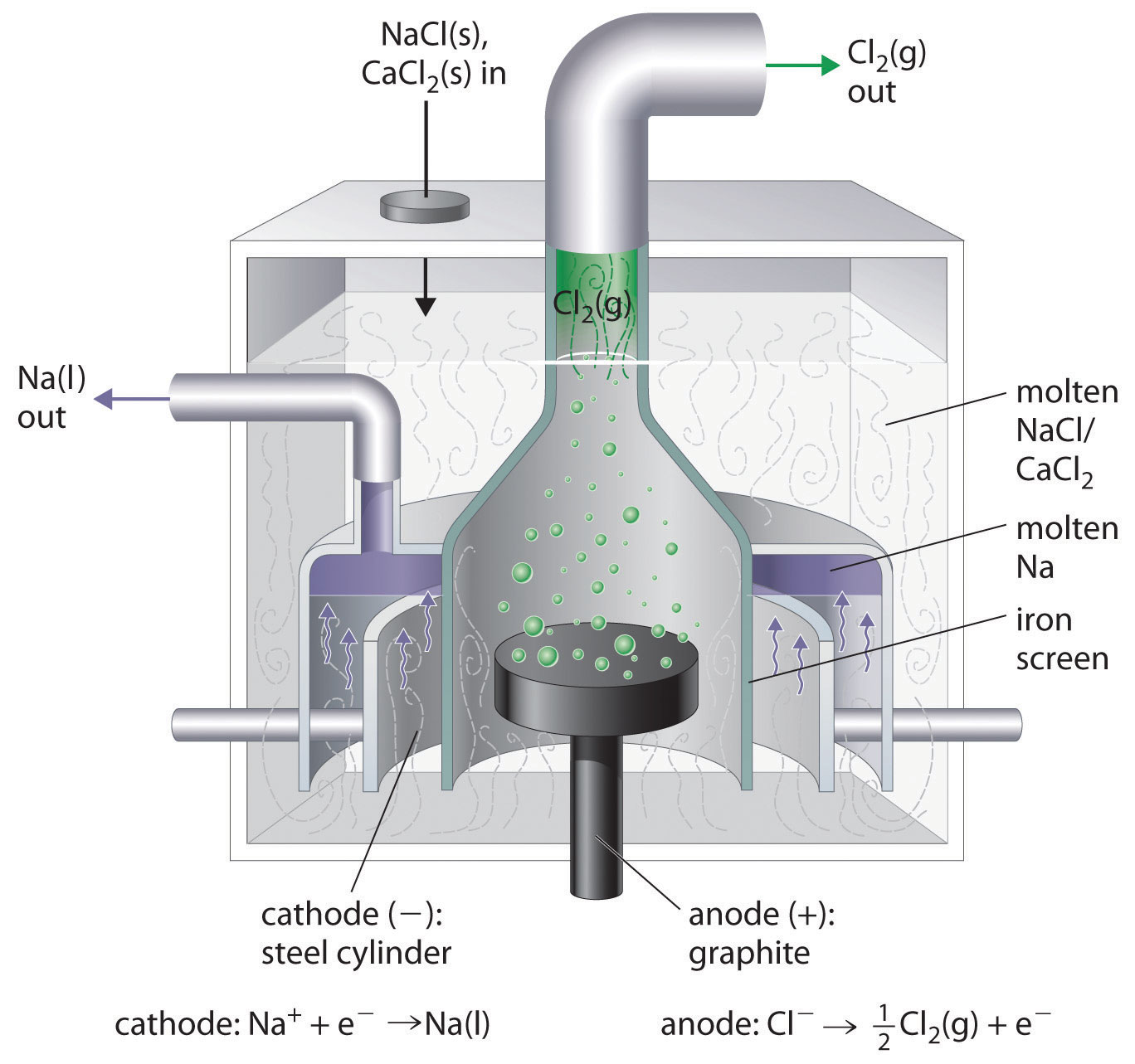
De manera similar, en el proceso Hall—Heroult utilizado para producir aluminio comercialmente, una mezcla fundida de aproximadamente 5% de óxido de aluminio (Al ₂ O ₃; punto de fusión = 2054°C) y 95% de criolita (Na ₃ AlF ₆; punto de fusión = 1012°C) se electroliza a aproximadamente 1000°C, produciendo fundido aluminio en el cátodo y gas CO ₂ en el ánodo de carbono. La reacción global es la siguiente:

\[\ce{2Al2O3(l) + 3C(s) -> 4Al(l) + 3CO2(g)} \label{20.9.7} \]

Los iones óxido reaccionan con carbono oxidado en el ánodo, produciendo CO ₂ (g).

Hay dos puntos importantes que hacer sobre estos dos procesos comerciales y sobre la electrólisis de sales fundidas en general.

1. Es probable que los potenciales de electrodo para sales fundidas sean muy diferentes de los potenciales celulares estándar enumerados en la Tabla P2, los cuales se compilan para la reducción de los iones hidratados en soluciones acuosas bajo condiciones estándar.
2. El uso de un sistema mixto de sales significa que existe la posibilidad de competencia entre diferentes reacciones electrolíticas. Cuando se electroliza una mezcla de NaCl y CaCl ₂, Cl ⁻ se oxida porque es el único anión presente, pero tanto Na ⁺ como Ca ^{2 +} pueden reducirse. Por el contrario, en el proceso Hall—Heroult solo está presente un catión que puede reducirse (Al ^{3 +}), pero hay tres especies que pueden oxidarse: C, O ²⁻ y F ⁻.

En el proceso Hall—Heroult, C se oxida en lugar de O ²⁻ o F ⁻ porque el oxígeno y el flúor son más electronegativos que el carbono, lo que significa que C es un oxidante más débil que O ₂ o F ₂. De manera similar, en la celda Downs, podríamos esperar que la electrólisis de una mezcla de NaCl/CaCl ₂ produzca calcio en lugar de sodio porque el Na es ligeramente menos electronegativo que el Ca (χ = 0.93 versus 1.00, respectivamente), haciendo que Na sea más fácil de oxidar y, por el contrario, Na ⁺ más difícil de reducir. De hecho, la reducción de Na ⁺ a Na es la reacción observada. En los casos en que las electronegatividades de dos especies son similares, otros factores, como la formación de iones complejos, adquieren importancia y pueden determinar el desenlace.

Ejemplo\(\PageIndex{1}\)

Si se electroliza una mezcla fundida de MgCl ₂ y KBr, ¿qué productos se formarán en el cátodo y el ánodo, respectivamente?

Dado: identidad de sales

Preguntado por: productos de electrólisis

Estrategia:

1. Enumere todos los posibles productos de reducción y oxidación. Con base en los valores de electronegatividad mostrados en la Figura 7.5, determinar qué especies se reducirán y qué especies se oxidarán.
2. Identificar los productos que se formarán en cada electrodo.

Solución

A Los posibles productos de reducción son Mg y K, y los posibles productos de oxidación son Cl ₂ y Br ₂. Debido a que el Mg es más electronegativo que K (χ = 1.31 versus 0.82), es probable que el Mg se reduzca en lugar de K. Debido a que Cl es más electronegativo que Br (3.16 versus 2.96), Cl ₂ es un oxidante más fuerte que Br ₂.

B Por lo tanto, la electrólisis producirá Br ₂ en el ánodo y Mg en el cátodo.

Ejercicio\(\PageIndex{1}\)

Predecir los productos si se electroliza una mezcla fundida de AlBr ₃ y LiF.

Contestar

Br ₂ y Al

La electrólisis también se puede utilizar para impulsar la descomposición termodinámicamente no espontánea del agua en sus elementos constituyentes: H ₂ y O ₂. Sin embargo, debido a que el agua pura es un conductor eléctrico muy pobre, primero se debe agregar una pequeña cantidad de un soluto iónico (como H _{2 SO 4 o Na 2 SO 4}) para aumentar su conductividad eléctrica. La inserción de electrodos inertes en la solución y la aplicación de un voltaje entre ellos dará como resultado la rápida evolución de burbujas de H ₂ y O ₂ (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): La electrólisis del agua. La aplicación de un potencial externo de aproximadamente 1.7—1.9 V a dos electrodos inertes sumergidos en una solución acuosa de un electrolito como H ₂ SO ₄ o Na ₂ SO ₄ impulsa la descomposición termodinámicamente no espontánea del agua en H ₂ en el cátodo y O ₂ en el ánodo. (CC BY-SA-NC; anónimo)

Las reacciones que ocurren son las siguientes:

• cátodo:\[2H^+_{(aq)} + 2e^− \rightarrow H_{2(g)} \;\;\; E^°_{cathode} = 0 V \label{20.9.8} \]
• ánodo:\[2H_2O_{(l)} → O_{2(g)} + 4H^+_{(aq)} + 4e^−\;\;\; E^°_{anode} = 1.23\; V \label{20.9.9} \]
• en general:\[2H_2O_{(l)} → O_{2(g)} + 2H_{2(g)}\;\;\; E^°_{cell} = −1.23 \;V \label{20.9.10} \]

Para un sistema que contiene un electrolito como Na ₂ SO ₄, que tiene un efecto despreciable en el equilibrio de ionización del agua líquida, el pH de la solución será de 7.00 y [H ⁺] = [OH ⁻] = 1.0 × 10 ⁻⁷. Suponiendo que\(P_\mathrm{O_2}\)\(P_\mathrm{H_2}\) = = 1 atm, podemos usar los potenciales estándar para calcular E para la reacción general:

\[\begin{align}E_\textrm{cell} &=E^\circ_\textrm{cell}-\left(\dfrac{\textrm{0.0591 V}}{n}\right)\log(P_\mathrm{O_2}P^2_\mathrm{H_2}) \\ &=-\textrm{1.23 V}-\left(\dfrac{\textrm{0.0591 V}}{4}\right)\log(1)=-\textrm{1.23 V}\end{align} \label{20.9.11} \]

Así, la _celda E es −1.23 V, que es el valor de la _celda E° si la reacción se lleva a cabo en presencia de H ⁺ 1 M en lugar de a pH 7.0.

En la práctica, se necesita un voltaje de aproximadamente 0.4—0.6 V mayor que el valor calculado para electrolizar el agua. Este voltaje agregado, llamado sobrevoltaje, representa la fuerza impulsora adicional requerida para superar barreras como la gran energía de activación para la formación de un gas en una superficie metálica. Se necesitan sobretensiones en todos los procesos electrolíticos, lo que explica por qué, por ejemplo, se deben aplicar aproximadamente 14 V para recargar la batería de 12 V en su automóvil.

En general, cualquier metal que no reaccione fácilmente con el agua para producir hidrógeno puede ser producido por la reducción electrolítica de una solución acuosa que contiene el catión metálico. Los metales del bloque p y la mayoría de los metales de transición se encuentran en esta categoría, pero los metales en estados de alta oxidación, que forman oxoaniones, no pueden reducirse al metal por simple electrólisis. Los metales activos, como el aluminio y los de los grupos 1 y 2, reaccionan tan fácilmente con el agua que solo pueden prepararse mediante la electrólisis de sales fundidas. De manera similar, cualquier elemento no metálico que no oxida fácilmente el agua a O ₂ se puede preparar mediante la oxidación electrolítica de una solución acuosa que contiene un anión apropiado. En la práctica, entre los no metales, solo F ₂ no se puede preparar usando este método. Los oxoaniones de no metales en sus estados de oxidación más altos, como NO ₃ ⁻, SO ₄ ^{2 −}, PO ₄ ^{3 −}, suelen ser difíciles de reducir electroquímicamente y generalmente se comportan como iones espectadores que permanecen en solución durante la electrólisis.

En general, cualquier metal que no reaccione fácilmente con el agua para producir hidrógeno puede ser producido por la reducción electrolítica de una solución acuosa que contiene el catión metálico.

Galvanoplastia

En un proceso llamado galvanoplastia, se deposita una capa de un segundo metal sobre el electrodo metálico que actúa como cátodo durante la electrólisis. La galvanoplastia se utiliza para mejorar la apariencia de los objetos metálicos y protegerlos de la corrosión. Ejemplos de galvanoplastia incluyen la capa de cromo que se encuentra en muchos accesorios de baño o (en días anteriores) en los parachoques y tapacubos de los automóviles, así como la fina capa de metal precioso que recubre vajillas o joyas plateadas. En todos los casos, el concepto básico es el mismo. En la Figura se muestra una vista esquemática de un aparato para galvanoplastia de platería y una fotografía de una celda de galvanoplastia comercial\(\PageIndex{4}\).

Figura\(\PageIndex{3}\): Galvanoplastia. (a) La galvanoplastia utiliza una celda electrolítica en la que el objeto que se va a chapar, como una horquilla, se sumerge en una solución del metal a depositar. El objeto que se está chapando actúa como cátodo, sobre el cual se deposita el metal deseado en una capa delgada, mientras que el ánodo generalmente consiste en el metal que se está depositando (en este caso, plata) que mantiene la concentración de la solución a medida que se disuelve. (b) En este aparato de galvanoplastia comercial, un gran número de objetos pueden ser chapados simultáneamente bajando el rack en la\(\ce{Ag^{+}}\) solución y aplicando el potencial correcto. (CC BY-SA-NC; anónimo)

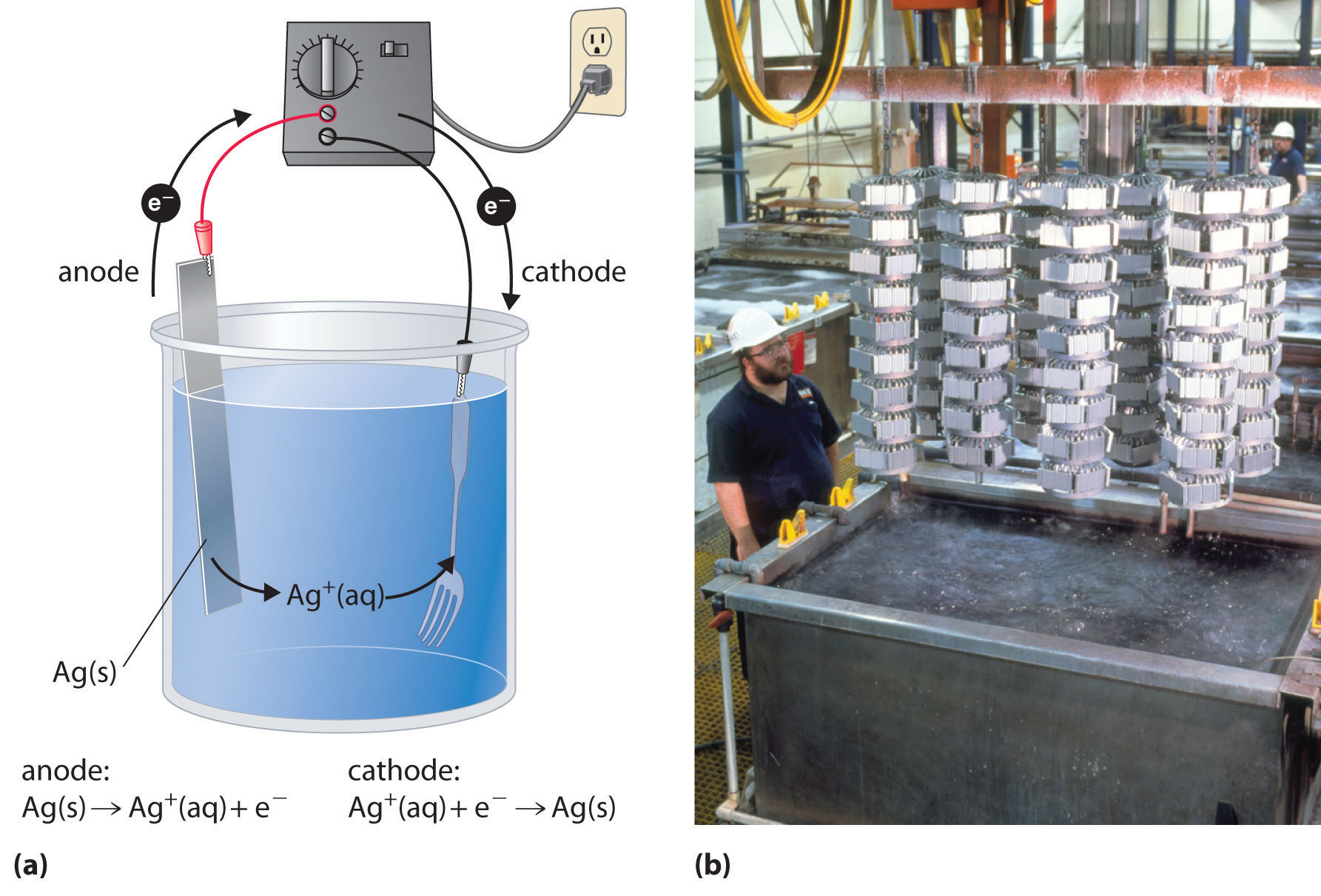
Las medias reacciones en la galvanoplastia de una horquilla, por ejemplo, con plata son las siguientes:

• cátodo (horquilla):\[\ce{Ag^{+}(aq) + e^{−} -> Ag(s)} \quad E°_{cathode} = 0.80 V\ \nonumber \]
• ánodo (barra de plata):\[\ce{Ag(s) -> Ag^{+}(aq) + e^{-}} \quad E°_{anode} = 0.80 V \nonumber \]

La reacción general es la transferencia de metal plateado de un electrodo (una barra de plata que actúa como ánodo) a otro (una horquilla que actúa como cátodo). Porque\(E^o_{cell} = 0\, V\), solo se necesita un pequeño voltaje aplicado para impulsar el proceso de galvanoplastia. En la práctica, se pueden agregar otras sustancias a la solución de chapado para controlar su conductividad eléctrica y regular la concentración de iones metálicos libres, asegurando así un recubrimiento suave y uniforme.

Consideraciones cuantitativas

Si conocemos la estequiometría de una reacción de electrólisis, la cantidad de corriente pasada y el tiempo, podemos calcular la cantidad de material consumido o producido en una reacción. Por el contrario, podemos usar la estequiometría para determinar la combinación de corriente y tiempo necesarios para producir una cantidad dada de material.

La cantidad de material que se oxida o reduce en un electrodo durante una reacción electroquímica está determinada por la estequiometría de la reacción y la cantidad de carga que se transfiere. Por ejemplo, en la reacción

\[\ce{Ag^{+}(aq) + e^{−} → Ag(s)} \nonumber \]

1 mol de electrones reduce 1 mol de\(\ce{Ag^{+}}\) a\(\ce{Ag}\) metal. En contraste, en la reacción

\[\ce{Cu^{2+}(aq) + 2e^{−} → Cu(s)} \nonumber \]

1 mol de electrones reduce solo 0.5 mol de\(\ce{Cu^{2+}}\) a\(\ce{Cu}\) metal. Recordemos que la carga en 1 mol de electrones es de 1 faraday (1 F), que es igual a 96,485 C. Por lo tanto, podemos calcular el número de moles de electrones transferidos cuando una corriente conocida pasa a través de una celda durante un periodo de tiempo determinado. La carga total (\(q\)en culombios) transferida es producto de la corriente (\(I\)en amperios) y el tiempo (\(t\), en segundos):

\[ q = I \times t \label{20.9.14} \]

La estequiometría de la reacción y la carga total transferida nos permiten calcular la cantidad de producto formado durante una reacción de electrólisis o la cantidad de metal depositado en un proceso de galvanoplastia.

Por ejemplo, si una corriente de 0.60 A pasa a través de una solución acuosa de\(\ce{CuSO4}\) por 6.0 min, el número total de culombios de carga que pasa a través de la celda es el siguiente:

\[\begin{align*} q &= \textrm{(0.60 A)(6.0 min)(60 s/min)} \\[4pt] &=\mathrm{220\;A\cdot s} \\[4pt] &=\textrm{220 C} \end{align*} \nonumber \]

Por lo tanto, el número de moles de electrones transferidos a\(\ce{Cu^{2+}}\) es

\[\begin{align*} \textrm{moles e}^- &=\dfrac{\textrm{220 C}}{\textrm{96,485 C/mol}} \\[4pt] &=2.3\times10^{-3}\textrm{ mol e}^- \end{align*} \nonumber \]

Debido a que se requieren dos electrones para reducir un solo ion Cu ^{2 +}, el número total de moles de Cu producidos es la mitad del número de moles de electrones transferidos, o 1.2 × 10 ⁻³ mol. Esto corresponde a 76 mg de Cu. En los procesos comerciales de electrorrefinación se utilizan corrientes mucho mayores (mayores o iguales a 50,000 A), correspondientes a aproximadamente 0.5 F/s, y los tiempos de reacción son del orden de 3—4 semanas.

Ejemplo\(\PageIndex{2}\)

Una cuchara plateada contiene típicamente alrededor de 2.00 g de Ag. Si se requieren 12.0 h para lograr el espesor deseado del recubrimiento de Ag, ¿cuál es la corriente promedio por cuchara que debe fluir durante el proceso de galvanoplastia, asumiendo una eficiencia del 100%?

Dado: masa de metal, tiempo y eficiencia

Preguntado por: actual requerido

Estrategia:

1. Calcular el número de moles de metal correspondientes a la masa transferida dada.
2. Escribir la reacción y determinar el número de moles de electrones requeridos para el proceso de galvanoplastia.
3. Utilice la definición del faraday para calcular el número de culombios requeridos. Después convierte los culombios a corriente en amperios.

Solución

A Primero debemos determinar el número de moles de Ag correspondientes a 2.00 g de Ag:

\(\textrm{moles Ag}=\dfrac{\textrm{2.00 g}}{\textrm{107.868 g/mol}}=1.85\times10^{-2}\textrm{ mol Ag}\)

B La reacción de reducción es Ag ⁺ (aq) + e ⁻ → Ag (s), por lo que 1 mol de electrones produce 1 mol de plata.

C Utilizando la definición del faraday,

culombios = (1.85 × 10 ^{− 2} mol e ⁻) (96.485 C/mol e ⁻) = 1.78 × 10 ³ C/mol

La corriente en amperios necesaria para entregar esta cantidad de carga en 12.0 h es por lo tanto

\ [\ begin {align*}\ textrm {amperios} &=\ dfrac {1.78\ tiempos10^3\ textrm {C}} {(\ textrm {12.0 h}) (\ textrm {60 min/h}) (\ textrm {60 s/min})}\\
& =4.12\ horas10^ {-2}\ textrm {C/s} =4.12\ tiempos10^ {-2}\ textrm {A}\ final {alinear*}\ nonumber\]

Debido a que el proceso de galvanoplastia suele ser mucho menos del 100% eficiente (los valores típicos están más cerca del 30%), la corriente real necesaria es mayor que 0.1 A.

Ejercicio\(\PageIndex{2}\)

Una lata típica de refresco de aluminio pesa alrededor de 29 g. ¿Cuánto tiempo se necesita para producir esta cantidad de Al (s) en el proceso Hall—Heroult, utilizando una corriente de 15 A para reducir una mezcla fundida de Al ₂ O ₃ /Na ₃ AlF ₆?

Contestar

5.8 h

Galvanoplastia: Galvanoplastia (se abre en una ventana nueva) [youtu.be]

Resumen

En la electrólisis, se aplica un voltaje externo para impulsar una reacción no espontánea. La cantidad de material oxidado o reducido puede calcularse a partir de la estequiometría de la reacción y la cantidad de carga transferida. Relación de carga, corriente y tiempo:

\[ q = I \times t \nonumber \]

En la electrólisis, se aplica un voltaje externo para impulsar una reacción no espontánea. La electrólisis también se puede utilizar para producir H ₂ y O ₂ a partir del agua. En la práctica, se debe aplicar una tensión adicional, llamada sobretensión, para superar factores como una gran energía de activación y un potencial de unión. La galvanoplastia es el proceso mediante el cual se deposita un segundo metal sobre una superficie metálica, mejorando así la apariencia de un objeto o brindando protección contra la corrosión. La cantidad de material consumido o producido en una reacción se puede calcular a partir de la estequiometría de una reacción de electrólisis, la cantidad de corriente pasada y la duración de la reacción electrolítica.