12.4: Leyes de tarifas integradas
- Page ID
- 75456
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Explicar la forma y función de una ley de tarifas integradas
- Realizar cálculos de ley de tasa integrada para reacciones de cero, primer y segundo orden
- Definir la vida media y realizar cálculos relacionados
- Identificar el orden de una reacción a partir de los datos de concentración/tiempo
Las leyes de tasas que hemos visto hasta ahora relacionan la tasa y las concentraciones de reactivos. También podemos determinar una segunda forma de cada ley de tasa que relaciona las concentraciones de reactivos y el tiempo. A estas se les llama leyes de tarifas integradas. Podemos usar una ley de velocidad integrada para determinar la cantidad de reactivo o producto presente después de un período de tiempo o para estimar el tiempo requerido para que una reacción continúe hasta cierto punto. Por ejemplo, se utiliza una ley de tasa integrada para determinar el tiempo que debe almacenarse un material radiactivo para que su radiactividad se descomponga a un nivel seguro.
Usando cálculo, la ley de velocidad diferencial para una reacción química puede integrarse con respecto al tiempo para dar una ecuación que relacione la cantidad de reactivo o producto presente en una mezcla de reacción con el tiempo transcurrido de la reacción. Este proceso puede ser muy sencillo o muy complejo, dependiendo de la complejidad de la ley de tasas diferenciales. Para fines de discusión, nos centraremos en las leyes de tarifas integradas resultantes para reacciones de primer, segundo y orden cero.
Reacciones de primer orden
Una ecuación\(k\) que relaciona la constante de velocidad con la concentración inicial\([A]_0\) y la concentración\([A]_t\) presente después de un tiempo dado se\(t\) puede derivar para una reacción de primer orden y demostrar que es:
\[\ln\left(\dfrac{[A]_t}{[A]_0}\right)=−kt \nonumber \]
o alternativamente
\[\ln\left(\dfrac{[A]_0}{[A]_t}\right)=kt \nonumber \]
o
\[[A]=[A]_0e^{−kt} \nonumber \]
La constante de velocidad para la descomposición de primer orden del ciclobutano,\(\ce{C4H8}\) a 500 °C es 9.2 × 10 −3 s −1:
\[\ce{C4H8⟶2C2H4} \nonumber \]
¿Cuánto tiempo tardará 80.0% de una muestra de C 4 H 8 en descomponerse?
Solución
Utilizamos la forma integrada de la ley tarifaria para responder preguntas relacionadas con el tiempo:
\[\ln\left(\dfrac{[A]_0}{[A]}\right)=kt \nonumber \]
Hay cuatro variables en la ley de tasas, así que si conocemos tres de ellas, podemos determinar la cuarta. En este caso conocemos [A] 0, [A], y k, y necesitamos encontrar t.
No se proporciona la concentración inicial de C 4 H 8, [A] 0, pero la provisión de que 80.0% de la muestra se ha descompuesto es información suficiente para resolver este problema. Sea x la concentración inicial, en cuyo caso la concentración después de 80.0% de descomposición es 20.0% de x o 0.200 x. Reorganizar la ley de velocidad para aislar t y sustituir las cantidades proporcionadas rinde:
\ [\ begin {align*}
t&=\ ln\ dfrac {[x]} {[0.200x]} ×\ dfrac {1} {k}\\ [4pt]
&=\ mathrm {\ ln\ dfrac {0.100\ :mol\: L^ {−1}} {0.020\ :mol\: L^ {−1}} ×\ dfrac {1} {9.2×10^ {−3}\ :s^ {−1}}}\\ [4pt]
&=\ mathrm {1.609 ×\ dfrac {1} {9.2×10^ {−3}\ :s^ {−1}}}\\ [4pt]
&=\ mathrm {1.7×10^ 2\ :s}
\ final {alinear*}\ nonumber\]
El yodo-131 es un isótopo radiactivo que se utiliza para diagnosticar y tratar algunas formas de cáncer de tiroides. El yodo-131 se desintegra a xenón-131 según la ecuación:
\[\textrm{I-131 ⟶ Xe-131 + electron} \nonumber \]
El decaimiento es de primer orden con una constante de velocidad de 0.138 d −1. Toda la desintegración radiactiva es de primer orden. ¿Cuántos días tardará el 90% del yodo−131 en una solución 0.500 M de esta sustancia en descomponerse a Xe-131?
- Contestar
-
16.7 días
Podemos usar leyes de velocidad integradas con datos experimentales que consisten en información de tiempo y concentración para determinar el orden y la constante de velocidad de una reacción. La ley de tasa integrada se puede reorganizar a un formato de ecuación lineal estándar:
\ [\ begin {align}
\ ln [A] & =( −k) (t) +\ ln [A] _0\ label {in1st}\\ [4pt]
y&=mx+b
\ end {align}\ nonumber\]
Una gráfica de\(\ln[A]\) versus\(t\) para una reacción de primer orden es una línea recta con una pendiente de\(−k\) y una intercepción de\(\ln[A]_0\). Si un conjunto de datos de velocidad se grafica de esta manera pero no dan como resultado una línea recta, la reacción no es de primer orden en\(A\).
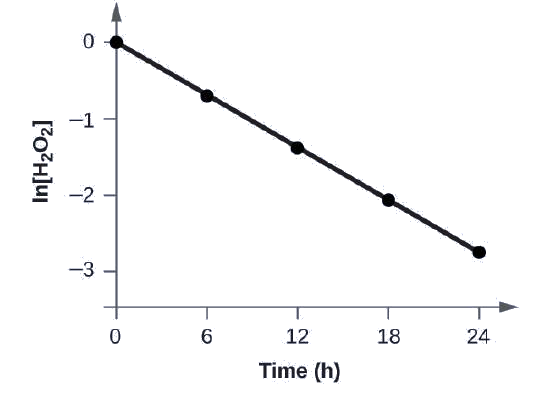
Demostrar que los datos de esta Figura pueden ser representados por una ley de tasa de primer orden graficando ln [H 2 O 2] versus tiempo. Determinar la constante de velocidad para la velocidad de descomposición de H 2 O 2 a partir de estos datos.
Solución
Los datos de esta Figura con la adición de valores de ln [H 2 O 2] se dan en la Figura\(\PageIndex{1}\).
| Juicio | Tiempo (h) | [H 2 O 2] (M) | ln [H 2 O 2] |
|---|---|---|---|
| 1 | 0 | 1.000 | 0.0 |
| 2 | 6.00 | 0.500 | −0.693 |
| 3 | 12.00 | 0.250 | −1.386 |
| 4 | 18.00 | 0.125 | −2.079 |
| 5 | 24.00 | 0.0625 | −2.772 |
La gráfica de ln [H 2 O 2] frente al tiempo es lineal, por lo que hemos verificado que la reacción puede ser descrita por una ley de tasa de primer orden.
La constante de velocidad para una reacción de primer orden es igual a la negativa de la pendiente de la parcela de ln [H 2 O 2] versus tiempo donde:
\[\ce{slope}=\dfrac{\textrm{change in }y}{\textrm{change in }x}=\dfrac{Δy}{Δx}=\dfrac{Δ\ln[\ce{H2O2}]}{Δt} \nonumber \]
Para determinar la pendiente de la línea, necesitamos dos valores de ln [H 2 O 2] a diferentes valores de t (uno cerca de cada extremo de la línea es preferible). Por ejemplo, el valor de ln [H 2 O 2] cuando t es 6.00 h es −0.693; el valor cuando t = 12.00 h es −1.386:
\ [\ begin {align*}
\ ce {pendiente} &=\ mathrm {\ dfrac {−1.386− (−0.693)} {12.00\: h−6.00\: h}}\\ [4pt]
&=\ mathrm {\ dfrac {−0.693} {6.00\: h}}\\ [4pt]
&=\ mathrm {−1.155×10^ {−2}\ :h^ {−1}}\\ [4pt]
k&=\ mathrm {−slope=− (−1.155×10^ {−1}\ :h^ {−1}) =1.155×10^ {−1}\ :h^ {−1} }
\ end {align*}\ nonumber\]
Grafique los siguientes datos para determinar si la reacción\(A⟶B+C\) es de primer orden.
| Juicio | Tiempo (s) | [A] |
|---|---|---|
| 1 | 4.0 | 0.220 |
| 2 | 8.0 | 0.144 |
| 3 | 12.0 | 0.110 |
| 4 | 16.0 | 0.088 |
| 5 | 20.0 | 0.074 |
- Contestar
-
La trama de ln [A] vs. t no es una línea recta. La ecuación no es de primer orden:
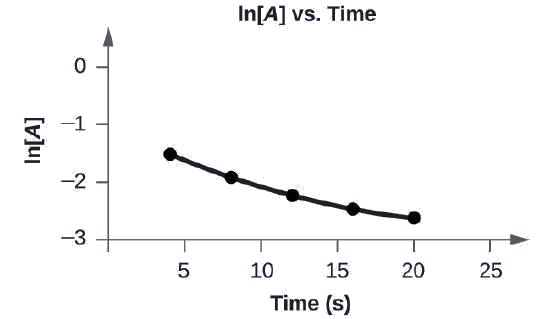
Se muestra una gráfica, etiquetada anteriormente como “l n [A] vs. Tiempo”. El eje x está etiquetado como “Tiempo (s)” y el eje y está etiquetado, “l n [A]”. El eje x muestra marcas a las 5, 10, 15, 20 y 25 horas. El eje y muestra marcas en negativo 3, negativo 2, negativo 1 y 0. Se dibuja una ligera curva conectando cinco puntos en coordenadas de aproximadamente (4, negativo 1.5), (8, negativo 2), (12, negativo 2.2), (16, negativo 2.4) y (20, negativo 2.6).
Reacciones de segundo orden
Las ecuaciones que relacionan las concentraciones de reactivos y la constante de velocidad de las reacciones de segundo orden son bastante complicadas. Nos limitaremos a las reacciones de segundo orden más simples, es decir, aquellas con tasas que dependen de la concentración de un solo reactivo y descritas por la ley de tasa diferencial:
\[\ce{Rate}=k[A]^2 \nonumber \]
Para estas reacciones de segundo orden, la ley de tarifas integradas es:
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \label{int2nd} \]
donde los términos de la ecuación tienen sus significados habituales definidos anteriormente.
La reacción del gas butadieno (C 4 H 6) consigo mismo produce gas C 8 H 12 de la siguiente manera:
\[\ce{2C4H6}(g)⟶\ce{C8H12(g)} \nonumber \]
La reacción es de segundo orden con una constante de velocidad igual a 5.76 × 10 −2 L/mol/min bajo ciertas condiciones. Si la concentración inicial de butadieno es 0.200 M, ¿cuál es la concentración restante después de 10.0 min?
Solución
Utilizamos la forma integrada de la ley tarifaria para responder preguntas sobre el tiempo. Para una reacción de segundo orden, tenemos:
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]
Conocemos tres variables en esta ecuación: [A] 0 = 0.200 mol/L, k = 5.76 × 10 −2 L/mol/min, y t = 10.0 min. Por lo tanto, podemos resolver para [A], la cuarta variable:
\ [\ begin {align*}
\ dfrac {1} {[A]} &=\ mathrm {(5.76×10^ {−2}\ :L\: mol^ {−1}\ :min^ {−1}) (10\ :min) +\ dfrac {1} {0.200\ :mol^ {−1}}}\\ [4pt]
\ dfrac {1} {[A]} &=\ mathrm {(5.76×10^ {−1}\ :L\: mol^ {−1}) +5.00\ :L\: mol^ {−1}}\\ [4pt]
\ dfrac {1} {[A]} &=\ mathrm {5.58\ :L\: mol^ {−1}}\\ [4pt]
[A] &=\ mathrm {1.79×10^ {−1}\ :mol\: L^ {−1}}
\ end {align*}\ nonumber\]
Por lo tanto 0.179 mol/L de butadieno permanecen al final de 10.0 min, en comparación con los 0.200 mol/L que originalmente estaban presentes.
Si la concentración inicial de butadieno es 0.0200 M, ¿cuál es la concentración restante después de 20.0 min?
- Contestar
-
0.0196 mol/L
La ley de tasa integrada para nuestras reacciones de segundo orden tiene la forma de la ecuación de una línea recta:
\ [\ begin {align*}
\ dfrac {1} {[A]} &=kt+\ dfrac {1} {[A] _0}\\ [4pt]
y&=mx+b
\ end {align*}\ nonumber\]
Una gráfica de\(\dfrac{1}{[A]}\) versus t para una reacción de segundo orden es una línea recta con una pendiente de k y una intercepción de\(\dfrac{1}{[A]_0}\). Si la trama no es una línea recta, entonces la reacción no es de segundo orden.
Pruebe los datos dados para mostrar si la dimerización de C 4H 6 es una reacción de primer o segundo orden.
Solución
| Juicio | Tiempo (s) | [C 4 H 6] (M) |
|---|---|---|
| 1 | 0 | 1.00 × 10 −2 |
| 2 | 1600 | 5.04 × 10 −3 |
| 3 | 3200 | 3.37 × 10 −3 |
| 4 | 4800 | 2.53 × 10 −3 |
| 5 | 6200 | 2.08 × 10 −3 |
Para distinguir una reacción de primer orden de una reacción de segundo orden, trazamos ln [C 4 H 6] versus t y la comparamos con una gráfica de\(\mathrm{\dfrac{1}{[C_4H_6]}}\) versus t. Los valores necesarios para estas parcelas siguen.
| Tiempo (s) | \(\dfrac{1}{[\ce{C4H6}]}\:(M^{−1})\) | ln [C 4 H 6] |
|---|---|---|
| 0 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">100 | −4.605 |
| 1600 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">198 | −5.289 |
| 3200 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">296 | −5.692 |
| 4800 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">395 | −5.978 |
| 6200 | \ (\ dfrac {1} {[\ ce {C4H6}]}\: (M^ {−1})\)” style="text-align:center; ">481 | −6.175 |
Las gráficas se muestran en la Figura\(\PageIndex{2}\). Como puede ver, la gráfica de ln [C 4 H 6] versus t no es lineal, por lo tanto la reacción no es de primer orden. La gráfica de\(\dfrac{1}{[\ce{C4H6}]}\) versus t es lineal, lo que indica que la reacción es de segundo orden.
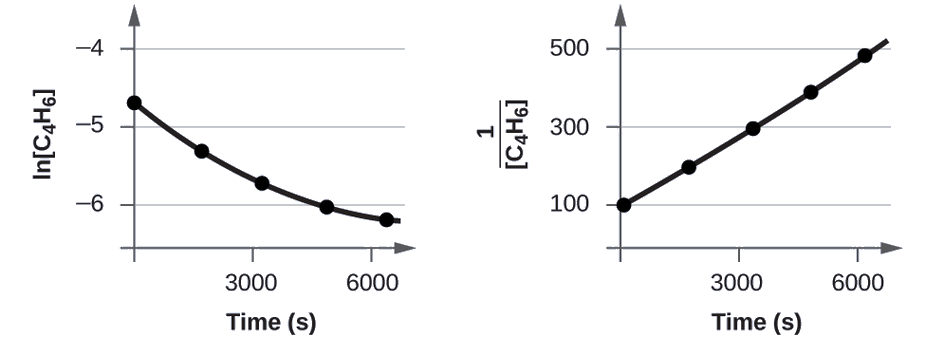
¿Los siguientes datos se ajustan a una ley de tasa de segundo orden?
| Juicio | Tiempo (s) | [A] (M) |
|---|---|---|
| 1 | 5 | 0.952 |
| 2 | 10 | 0.625 |
| 3 | 15 | 0.465 |
| 4 | 20 | 0.370 |
| 5 | 25 | 0.308 |
| 6 | 35 | 0.230 |
- Contestar
-
Sí. La gráfica de\(\dfrac{1}{[A]}\) vs. t es lineal:
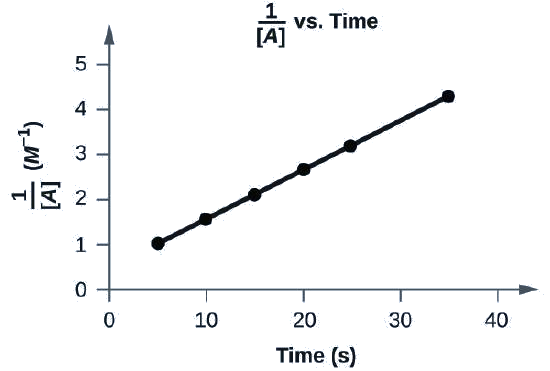
Se muestra una gráfica, con el título “1 dividido por [A] vs. Tiempo”, con la etiqueta, “Tiempo (s)”, en el eje x. La etiqueta “1 dividido por [A]” aparece a la izquierda del eje y. El eje x muestra marcas comenzando en cero y continuando a intervalos de 10 hasta e incluyendo 40. El eje y de la izquierda muestra marcas comenzando en 0 y aumentando en intervalos de 1 hasta e incluyendo 5. Una línea con tendencia al alza se traza a través de seis puntos aproximadamente en (4, 1), (10, 1.5), (15, 2.2), (20, 2.8), (26, 3.4) y (36, 4.4).
Reacciones de orden cero
Para las reacciones de orden cero, la ley de tasa diferencial es:
\[\ce{Rate}=k[A]^0=k \nonumber \]
Por lo tanto, una reacción de orden cero exhibe una velocidad de reacción constante, independientemente de la concentración de sus reactivos.
La ley de velocidad integrada para una reacción de orden cero también tiene la forma de la ecuación de una línea recta:
\ [\ begin {align*}
[A] &=−kt+ [A] _0\ label {intzero}\\ [4pt]
y&=mx+b
\ end {align*}\ nonumber\]
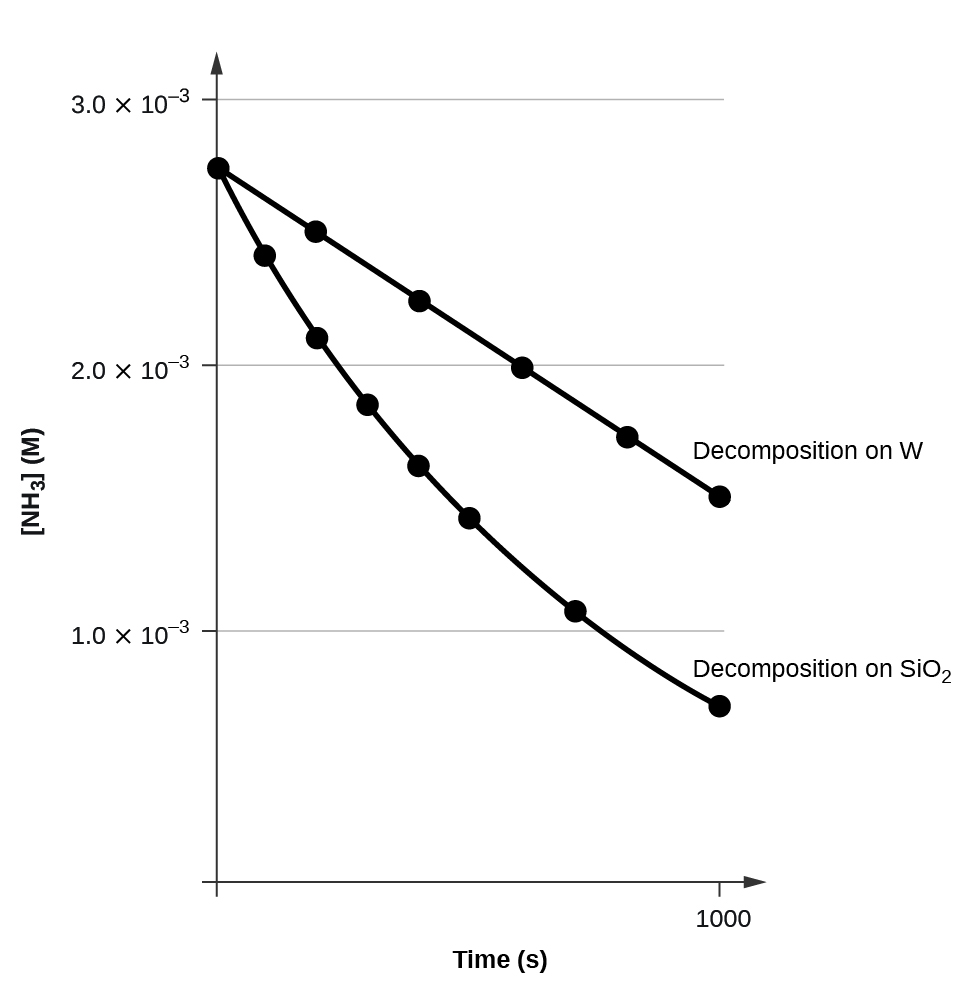
Una gráfica de\([A]\) versus\(t\) para una reacción de orden cero es una línea recta con una pendiente de −k y una intercepción de [A] 0. La figura\(\PageIndex{3}\) muestra una gráfica de [NH 3] versus t para la descomposición de amoníaco en un alambre de tungsteno caliente y para la descomposición de amoníaco en cuarzo caliente (SiO 2). La descomposición de NH 3 sobre tungsteno caliente es de orden cero; la trama es una línea recta. La descomposición del NH 3 en cuarzo caliente no es de orden cero (es de primer orden). A partir de la pendiente de la línea para la descomposición de orden cero, podemos determinar la constante de velocidad:
\[\ce{slope}=−k=\mathrm{1.3110^{−6}\:mol/L/s} \nonumber \]
La vida media de una reacción
La vida media de una reacción (t 1/2) es el tiempo requerido para que se consuma la mitad de una cantidad dada de reactivo. En cada vida media sucesiva, se consume la mitad de la concentración restante del reactivo. Usando como ejemplo la descomposición del peróxido de hidrógeno, encontramos que durante la primera vida media (de 0.00 horas a 6.00 horas), la concentración de H 2 O 2 disminuye de 1.000 M a 0.500 M. Durante la segunda vida media (de 6.00 horas a 12.00 horas), disminuye de 0.500 M a 0.250 M; durante la tercera semivida, disminuye de 0.250 M a 0.125 M. La concentración de H 2 O 2 disminuye a la mitad durante cada periodo sucesivo de 6.00 horas. La descomposición del peróxido de hidrógeno es una reacción de primer orden y, como se puede demostrar, la vida media de una reacción de primer orden es independiente de la concentración del reactivo. Sin embargo, las semividas de las reacciones con otros órdenes dependen de las concentraciones de los reactivos.
Reacciones de primer orden
Podemos derivar una ecuación para determinar la vida media de una reacción de primer orden a partir de la forma alternativa de la ley de tasa integrada de la siguiente manera:
\ [\ begin {align*}
\ ln\ dfrac {[A] _0} {[A]} &=kt\\ [4pt]
t&=\ ln\ dfrac {[A] _0} {[A]} ×\ dfrac {1} {k}
\ end {align*}\ nonumber\]
Si establecemos el tiempo t igual a la vida media\(t_{1/2}\),, la concentración correspondiente de A en este momento es igual a la mitad de su concentración inicial. De ahí, cuando\(t=t_{1/2}\),\([A]=\dfrac{1}{2}[A]_0\).
Por lo tanto:
\ [\ begin {alinear*}
t_ {1/2} &=\ ln\ dfrac {[A] _0} {\ dfrac {1} {2} [A] _0} ×\ dfrac {1} {k}\\ [4pt]
&=\ ln 2×\ dfrac {1} {k} =0.693×\ dfrac {1} {k}
\ final {alinear*}\ nonumber\]
Así:
\[t_{1/2}=\dfrac{0.693}{k} \nonumber \]
Podemos ver que la vida media de una reacción de primer orden es inversamente proporcional a la constante de velocidad k. Una reacción rápida (vida media más corta) tendrá una k mayor; una reacción lenta (vida media más larga) tendrá una k más pequeña.
Calcular la constante de velocidad para la descomposición de primer orden del peróxido de hidrógeno en agua a 40 °C, utilizando los datos dados en la Figura\(\PageIndex{4}\).
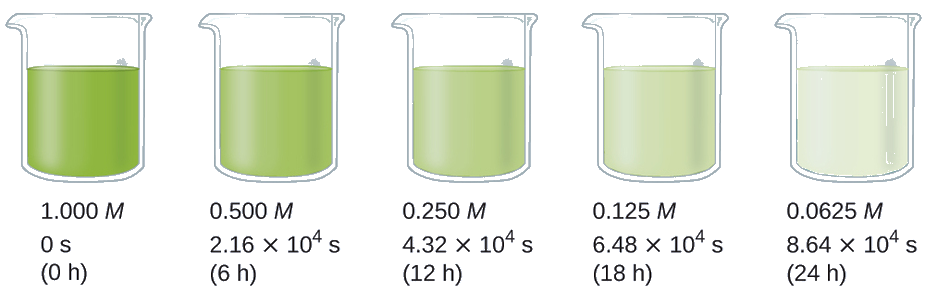
Solución La vida media para la descomposición de H 2 O 2 es 2.16 × 10 4 s:
\ [\ begin {align*}
t_ {1/2} &=\ dfrac {0.693} {k}\\\ [4pt]
k&=\ dfrac {0.693} {t_ {1/2}} =\ dfrac {0.693} {2.16×10^4\:\ ce s} =3.21×10^ {−5}\:\ ce s^ {−1}
\ end alinear*}\ nonumber\]
La desintegración radiactiva de primer orden del yodo-131 presenta una constante de velocidad de 0.138 d −1. ¿Cuál es la vida media de esta decadencia?
- Contestar
-
5.02 d.
Reacciones de segundo orden
Podemos derivar la ecuación para calcular la vida media de un segundo orden de la siguiente manera:
\[\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0} \nonumber \]
o
\[\dfrac{1}{[A]}−\dfrac{1}{[A]_0}=kt \nonumber \]
Si
\[t=t_{1/2} \nonumber \]
entonces
\[[A]=\dfrac{1}{2}[A]_0 \nonumber \]
y podemos escribir:
\ dfrac {1} {\ dfrac {1} {2} [A] _0} −\ dfrac {1} {[A] _0} &=kt_ {1/2}\\ [4pt]
2 [A] _0−\ dfrac {1} {[A] _0} &=kt_ {1/2}\\ [4pt]
\ dfrac {1} {[A] _0} &=kt_ {1/2}
\ final {alinear*}\)
Así:
\[t_{1/2}=\dfrac{1}{k[A]_0} \nonumber \]
Para una reacción de segundo orden,\(t_{1/2}\) es inversamente proporcional a la concentración del reactivo, y la vida media aumenta a medida que avanza la reacción debido a que la concentración de reactivo disminuye. En consecuencia, encontramos que el uso del concepto de vida media es más complejo para reacciones de segundo orden que para reacciones de primer orden. A diferencia de las reacciones de primer orden, la constante de velocidad de una reacción de segundo orden no puede calcularse directamente a partir de la semivida a menos que se conozca la concentración inicial.
Reacciones de orden cero
Podemos derivar una ecuación para calcular la vida media de una reacción de orden cero de la siguiente manera:
\[[A]=−kt+[A]_0 \nonumber \]
Cuando se haya consumido la mitad de la cantidad inicial de reactivo\(t=t_{1/2}\) y\([A]=\dfrac{[A]_0}{2}\). Así:
\ [\ begin {align*}
\ dfrac {[A] _0} {2} &=−kt_ {1/2} + [A] _0\\ [4pt]
kt_ {1/2} &=\ dfrac {[A] _0} {2}
\ end {align*}\ nonumber\]
y
\[t_{1/2}=\dfrac{[A]_0}{2k} \nonumber \]
La vida media de una reacción de orden cero aumenta a medida que aumenta la concentración inicial. Las ecuaciones para las leyes de tasas tanto diferenciales como integradas y las semividas correspondientes para las reacciones de cero, primer y segundo orden se resumen en la Tabla\(\PageIndex{1}\).
| Orden cero | Primer orden | Segundo orden | |
|---|---|---|---|
| ley de tarifas | tasa = k | tasa = k [A] | tasa = k [A] 2 |
| unidades de constante de velocidad | M s −1 | s −1 | M −1 s −1 |
| ley de tasa integrada | [A] = − kt + [A] 0 | ln [A] = − kt + ln [A] 0 | \(\dfrac{1}{[A]}=kt+\left(\dfrac{1}{[A]_0}\right)\) |
| trazado necesario para el ajuste lineal de los datos de velocidad | [A] vs. t | Ln [A] vs. t | \(\dfrac{1}{[A]}\)vs. t |
| relación entre pendiente de trazado lineal y constante de velocidad | k = −pendiente | k = −pendiente | k = +pendiente |
| vida media | \(t_{1/2}=\dfrac{[A]_0}{2k}\) | \(t_{1/2}=\dfrac{0.693}{k}\) | \(t_{1/2}=\dfrac{1}{[A]_0k}\) |
Resumen
Las leyes de tasas diferenciales pueden ser determinadas por el método de tasas iniciales u otros métodos. Medimos valores para las velocidades iniciales de una reacción a diferentes concentraciones de los reactivos. A partir de estas mediciones, se determina el orden de la reacción en cada reactivo. Las leyes de tarifas integradas están determinadas por la integración de las leyes de tasas diferenciales correspondientes. Las constantes de velocidad para esas leyes de velocidad se determinan a partir de mediciones de concentración en diversos momentos durante una reacción.
La vida media de una reacción es el tiempo requerido para disminuir la cantidad de un reactivo dado a la mitad. La vida media de una reacción de orden cero disminuye a medida que disminuye la concentración inicial del reactivo en la reacción. La vida media de una reacción de primer orden es independiente de la concentración, y la vida media de una reacción de segundo orden disminuye a medida que aumenta la concentración.
Ecuaciones Clave
- ley de tasa integrada para reacciones de orden cero (Ecuación\ ref {intzero}):
\([A]=−kt+[A]_0\)con\(t_{1/2}=\dfrac{[A]_0}{2k}\)
- ley de tasa integrada para reacciones de primer orden (Ecuación\ ref {in1st}):
\(\ln[A]=−kt+ \ln[A]_0\)con\(t_{1/2}=\dfrac{0.693}{k}\)
- ley de tasa integrada para reacciones de segundo orden (Ecuación\ ref {int2nd}):
\(\dfrac{1}{[A]}=kt+\dfrac{1}{[A]_0}\)con\(t_{1/2}=\dfrac{1}{[A]_0k}\)
Glosario
- vida media de una reacción (t l/2)
- tiempo requerido para que se consuma la mitad de una cantidad dada de reactivo
- ley de tasa integrada
- ecuación que relaciona la concentración de un reactivo con el tiempo transcurrido de reacción


