4.3: El modelo de aprendizaje de atractores contrastivos extendidos (XCAL)

La función de aprendizaje que adoptamos para los modelos en el resto de este texto se denomina regla eXtended Contrastive Atractor Learning (XCAL). (Las bases para esta denominación quedarán claras más adelante). Esta función de aprendizaje se derivó a través de una convergencia de enfoques de abajo hacia arriba (motivados por consideraciones biológicas detalladas) y de arriba hacia abajo (motivados por desideratas computacionales). En la derivación de abajo hacia arriba, se extrajo una función de aprendizaje empírico (llamada función XCAL dWt) a partir de un modelo computacional altamente biológicamente detallado de los mecanismos de plasticidad sináptica conocidos, por Urakubo, Honda, Froemke, & Kuroda (2008) (ver Biología detallada del aprendizaje para más detalles). Su modelo se basa en parámetros detallados de velocidad química y constantes de difusión, etc., basados en mediciones empíricas, para todos los principales procesos biológicos involucrados en la plasticidad sináptica. Capturamos gran parte de la increíble complejidad del modelo Urakubo, Honda, Froemke, & Kuroda (2008) (y por extensión, ojalá, la complejidad de los mecanismos reales de plasticidad sináptica en el cerebro) utilizando una simple función lineal, que se muestra a continuación, que emerge de él. Esta función XCAL dWt se parece mucho a la función mostrada en la Figura 4.2, representando la dependencia de la plasticidad sináptica en los niveles de Ca++. También se parece mucho a la función de aprendizaje Bienenstock, Cooper, & Munro (1982) (BCM).

El enfoque de arriba hacia abajo aprovecha la idea clave detrás de la función de aprendizaje BCM, que es el uso de un umbral flotante para determinar la cantidad de actividad necesaria para provocar LTP vs LTD (ver Figura 4.2). Específicamente, el umbral no se fija en un valor particular, sino que se ajusta en función de los niveles de actividad promedio de la neurona postsináptica en cuestión durante un largo periodo de tiempo, dando como resultado una dinámica homeostática. Las neuronas que han estado relativamente inactivas pueden aumentar más fácilmente sus pesos sinápticos a niveles de actividad más bajos, y así pueden “volver al juego”. Por el contrario, las neuronas que han sido relativamente hiperactivas tienen más probabilidades de disminuir sus pesos sinápticos, y “dejar de acaparar todo”.

Como veremos a continuación, esta función contribuye a un útil aprendizaje autoorganizado, donde diferentes neuronas vienen a extraer distintos aspectos de la estructura estadística en un entorno dado. Pero los mecanismos puramente autoorganizativos están fuertemente limitados en lo que pueden aprender —son impulsados por generalidades estadísticas (por ejemplo, los animales tienden a tener cuatro patas), y son incapaces de adaptarse de manera más pragmática a las demandas funcionales que enfrenta el organismo. Por ejemplo, algunos objetos son más importantes de reconocer que otros (por ejemplo, amigos y enemigos son importantes, plantas aleatorias o trozos de basura o escombros, no tanto).

Para lograr estos objetivos más pragmáticos, necesitamos un aprendizaje impulsado por errores, donde el aprendizaje se centre específicamente en corregir errores, no solo categorizar patrones estadísticos. Afortunadamente, podemos usar el mismo mecanismo de umbral flotante para lograr un aprendizaje impulsado por errores dentro del mismo marco matemático general, adaptando el umbral en una escala de tiempo más rápida. En este caso, los pesos se incrementan si los estados de actividad son mayores que sus niveles muy recientes, y a la inversa, los pesos disminuyen si los niveles de actividad bajan en relación con estados anteriores. Así, podemos pensar que los niveles de actividad recientes (el umbral) reflejan expectativas que posteriormente se comparan con los resultados reales, con la diferencia (o “error”) impulsando el aprendizaje. Debido a que ambas formas de aprendizaje (autoorganizativas e impulsadas por errores) son bastante útiles, y utilizan exactamente el mismo marco matemático, las integramos en un solo conjunto de ecuaciones con dos umbrales que reflejan niveles de actividad integrados en diferentes escalas de tiempo (promedio reciente y promedio a largo plazo).

A continuación, describimos la función XCAL DWt (DWt = cambio de peso), antes de describir cómo captura ambas formas de aprendizaje, seguido de su integración en un único marco unificado (¡incluyendo la explicación prometida para su nombre!).

La función XCAL DWt

Figura\(4.4\): La función XCAL dWt, que muestra dirección y magnitud de los cambios sinápticos de peso (dWt) en función de la actividad promedio a corto plazo de la neurona remitente (\(x\)) veces la neurona receptora (\(y\)). Esta cantidad es una simple aproximación matemática al nivel de Ca++ postsináptico, reflejando la dependencia del canal NMDA tanto en el envío como en la recepción de la actividad neuronal. Esta función se extrajo directamente del modelo biofísico detallado Urakubo, Honda, Froemke, & Kuroda (2008), ajustando una función lineal por tramos al comportamiento sináptico de cambio de peso que emerge de ella en función de una amplia gama de patrones de espigas de envío y recepción.

La función XCAL DWt extraída del modelo Urakubo, Honda, Froemke y Kuroda (2008) se muestra en la Figura 4.4. En primer lugar, la entrada principal a esta función es la actividad sináptica total que refleja la velocidad de disparo y la duración de la actividad de las neuronas emisoras y receptoras. En términos matemáticos para un modelo de código de tarifa con tasa de actividad de envío x y tasa de actividad de recepción y, este sería simplemente el producto “Hebbian” que describimos anteriormente:

• \(\Delta w=f_{x c a l}\left(x y, \theta_{p}\right)\)

donde\(f_{x c a l}\) es la función lineal por tramos que se muestra en la Figura 4.4. El cambio de peso también depende de un parámetro de umbral dinámico adicional\(\theta_{p}\), que determina el punto en el que cruza de cambios de peso negativos a positivos, es decir, el punto en el que el peso cambia el signo inverso. Para completar, aquí está la expresión matemática de esta función, pero solo necesitas entender su forma como se muestra en la figura:

• \(f_{x c a l}\left(x y, \theta_{p}\right)=\left\{\begin{array}{ll}{\left(x y-\theta_{p}\right)} & {\text { if } x y>\theta_{p} \theta_{d}} \\ {-x y\left(1-\theta_{d}\right) / \theta_{d}} & {\text { otherwise }}\end{array}\right.\)

donde\(\theta_{d}=.1\) es una constante que determina el punto donde la función invierte la dirección (es decir, de vuelta hacia cero dentro del régimen de disminución de peso) — este punto de inversión ocurre en\(\theta_{p} \theta_{d}\), de manera que se adapta de acuerdo al\(\theta_{p}\) valor dinámico.

Como se señaló en la sección anterior, la dependencia del canal NMDA de la actividad tanto de las neuronas emisoras como receptoras se puede resumir con este sencillo producto hebbio, y es probable que el nivel de Ca++ intracelular refleje este valor. Así, la función XCAL dWt tiene muy buen sentido en estos términos: refleja la naturaleza cualitativa de los cambios de peso en función del Ca++ que se ha establecido a partir de estudios empíricos y postulado por otros modelos teóricos durante mucho tiempo. El modelo Urakubo simula efectos detallados del tiempo de pico pre/postsináptico en los niveles de Ca++ y LTP/LTD asociados, pero lo que surge de estos efectos a nivel de tasas de disparo es esta función fundamental mucho más simple.

Como función de aprendizaje, esta función básica de XCAL DWt tiene algunas ventajas sobre una función hebbiana simple, al tiempo que comparte su naturaleza básica debido al término “pre * post” en su núcleo. Por ejemplo, debido a la forma de la función DWt, los pesos bajarán y subirán, mientras que la función hebbiana solo hace que los pesos aumenten. Pero aún tiene el problema de que los pesos aumentarán sin límite (siempre y cuando los niveles de actividad sean a menudo mayores que el umbral). Veremos en la siguiente sección que algunas otras modificaciones computacionalmente motivadas de arriba hacia abajo pueden resultar en una forma de aprendizaje más poderosa mientras se mantiene esta forma básica.

Aprendizaje autoorganizado: escalas de tiempo largo y el modelo BCM

Figura\(4.5\): La forma de la función de aprendizaje BCM. Obsérvese la similitud en la forma cualitativa tanto con la función XCAL dWt como con la plasticidad sináptica como función de Ca++.

La mayor motivación computacional proviene de una línea de funciones de aprendizaje que comenzó con Bienenstock, Cooper, & Munro (1982), con estas iniciales dando lugar al nombre de la función: BCM. (Curiosamente Leon Cooper, un Nobel Laurato en Física, también fue “central” en la teoría de la superconductividad BCS). La función BCM es una forma modificada de aprendizaje hebbio, que incluye un interesante mecanismo homeostático que evita que las neuronas individuales disparen demasiado o muy poco con el tiempo:

• \(\Delta w=x y(y-\theta)\)

donde de nuevo\(x\) = actividad de envío,\(y\) = actividad receptora, y\(\theta\) es un umbral flotante que refleja un promedio de largo tiempo de la actividad de la neurona receptora:

• \(\theta=\left\langle y^{2}\right\rangle\)

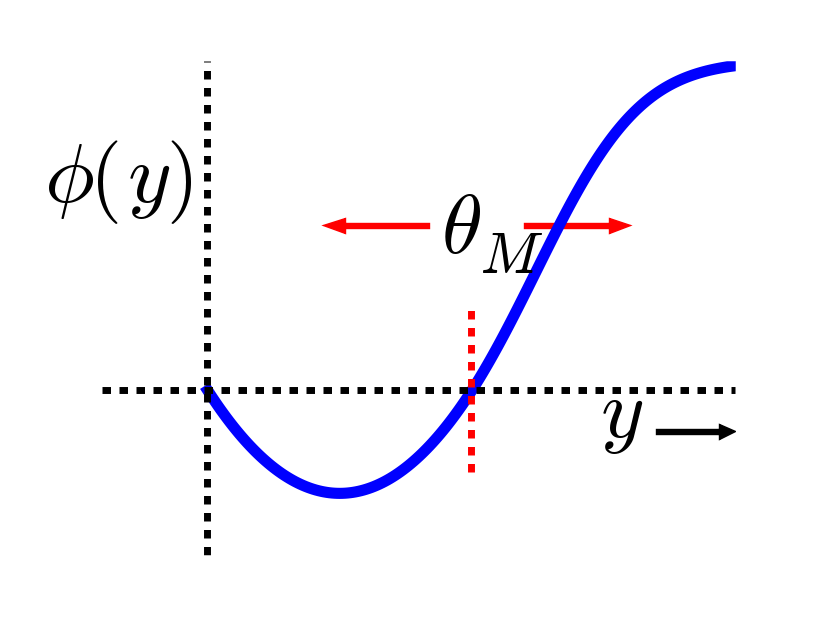
donde\(\langle \rangle\) indica el valor esperado o promedio, en este caso del cuadrado de la activación de la neurona receptora. La Figura 4.5 muestra cómo se ve esta función en general, una forma que debería ser bastante familiar. De hecho, el hecho de que la función de aprendizaje BCM anticipara la naturaleza cualitativa de la plasticidad sináptica en función del Ca++ (Figura 4.2) es una sorprendente instancia de presciencia teórica. Además, investigadores de BCM han demostrado que hace un buen trabajo al dar cuenta de diversos fenómenos de aprendizaje conductual, proporcionando un mejor ajuste que un mecanismo de aprendizaje hebbio comparable (Figura 4.6, (Cooper, Intrator, Blais, & Shouval, 2004)).

Figura\(4.6\): Datos de plasticidad sináptica de ratas criadas en la oscuridad (círculos rellenos) y normalmente criadas (círculos abiertos), mostrando que las ratas de crianza oscura parecen tener un umbral más bajo para LTP, consistente con el umbral flotante BCM. Las neuronas en estos animales son presumiblemente mucho menos activas en general, y por lo tanto su umbral se mueve hacia abajo, haciéndolos más propensos a exhibir LTP en relación con LTD. Reproducido de Kirkwood, Rioult, & Bear (1996).

El BCM se ha aplicado típicamente en redes de alimentación directa simples en las que, dado un patrón de entrada, solo hay un valor de activación para cada neurona. Pero, ¿cómo deben actualizarse los pesos en un sistema más realista conectado bidireccionalmente con dinámicas atractores en las que los estados de actividad evolucionan continuamente a través del tiempo? Enfrentamos este tema en la versión XCAL de las ecuaciones BCM:

• \(\Delta w=f_{x c a l}\left(x y,\langle y\rangle_{l}\right)=f_{x c a l}\left(x y, y_{l}\right)\)

donde\(x y\) se entiende como la actividad sináptica promedio a corto plazo (en una escala de tiempo de unos pocos cientos de milisegundos, la escala de tiempo de acumulación de Ca++ que impulsa la plasticidad sináptica), que podría expresarse más formalmente como:\(\langle x y\rangle_{s}\), y\(y_{l}=\langle y\rangle_{l}\) es el largo plazo actividad promedio de la neurona postsináptica (es decir, esencialmente la misma que en BCM, pero sin la cuadratura), que desempeña el papel del valor umbral\(\theta_{p}\) flotante en la función XCAL.

Después de una considerable experimentación, hemos encontrado la siguiente manera de calcular el umbral\(y_{l}\) flotante para proporcionar la mejor capacidad para controlar el umbral y lograr la mejor dinámica de aprendizaje general:

• \(\begin{array}{l}{\text { if } y>.2 \text { then } y_{l}=y_{l}+\frac{1}{\tau_{l}}\left(\max -y_{l}\right)} \\ {\text { else } y_{l}=y_{l}+\frac{1}{\tau}\left(\min -y_{l}\right)}\end{array}\)

Esto produce un enfoque exponencial bien controlado para los extremos máximo o mínimo dependiendo de si la actividad de la unidad receptora excede el umbral de actividad básica de .2. La constante de tiempo para la integración\(\tau_{l}\) es de 10 por defecto, integrando en alrededor de 10 pruebas. Consulte el subtema XCAL_Details para más discusión.

Figura\(4.7\): Cómo el umbral flotante en función de la actividad neuronal promedio a largo plazo del receptor\(\langle y\rangle_{l}\) impulsa el comportamiento homeostático. Las neuronas que tienen baja actividad promedio tienen muchas más probabilidades de aumentar sus pesos porque el umbral es bajo, mientras que las que tienen una actividad promedio alta tienen muchas más probabilidades de disminuir sus pesos debido a que el umbral es alto.

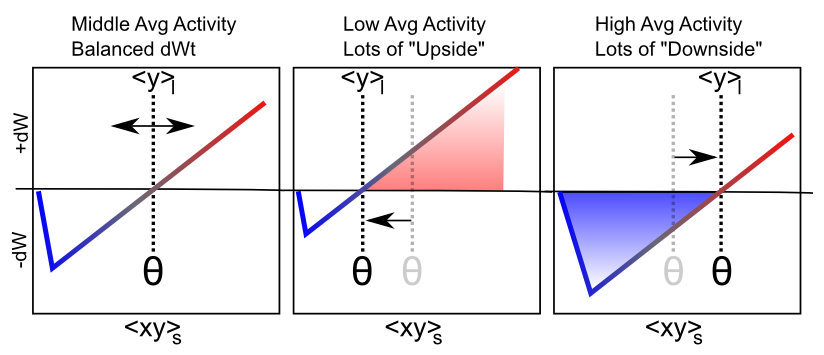
La Figura 4.7 muestra el principal comportamiento cualitativo de este mecanismo de aprendizaje: cuando la actividad promedio a largo plazo del receptor es baja, el umbral baja, y por lo tanto es más probable que el valor de la actividad sináptica a corto plazo caiga en el territorio de cambio de peso positivo. Esto tenderá a aumentar los pesos sinápticos en general, y así hacer que la neurona sea más propensa a activarse en el futuro, logrando el objetivo homeostático. Por el contrario, cuando la actividad promedio a largo plazo del receptor es alta, el umbral también es alto y, por lo tanto, la actividad sináptica a corto plazo es más probable que impulse disminuciones de peso que aumentos. Esto llevará a estas neuronas hiperactivas por una muesca o dos, para que no terminen dominando la actividad de la red.

Dinámica de aprendizaje autoorganizativa

Esta capacidad de difundir la actividad neuronal alrededor de una manera más equitativa resulta ser crítica para el aprendizaje autoorganizado, ya que permite a las neuronas cubrir de manera más eficiente y efectiva el espacio de las cosas a representar. Para ver por qué, aquí están los elementos críticos de la dinámica de aprendizaje autoorganizada (ver exploración de simulación posterior para realmente tener una idea de cómo funciona todo esto en la práctica):

• Competencia inhibitoria: solo las neuronas impulsadas más fuertemente superan el umbral inhibitorio y pueden activarse. Estos son aquellos cuyos pesos sinápticos actuales se ajustan mejor (“detectan”) el patrón de entrada actual.
• Los ricos obtienen un bucle de retroalimentación positiva más rico: debido a la naturaleza de la función de aprendizaje, solo aquellas neuronas que realmente se activan son capaces de aprender (cuando la actividad del receptor y = 0, luego xy = 0 también, y la función XCAL DWt es 0 a 0). Así, las neuronas que ya detectan mejor la entrada de corriente son las que consiguen fortalecer aún más su capacidad para detectar estas entradas. Esta es la visión esencial que tuvo Hebb sobre por qué la función de aprendizaje hebbiano debería fortalecer un “engrama”.
• homeostasis para equilibrar el bucle de retroalimentación positiva — si se deja sin marcar, la dinámica rich-get-richer termina con unas pocas unidades dominando todo, y como resultado, todas las entradas se clasifican en una categoría inútil, demasiado amplia (“todo”). El mecanismo homeostático en BCM ayuda a combatir esto al elevar el umbral flotante para las neuronas altamente activas, haciendo que sus pesos disminuyan para todos menos sus patrones de entrada más preferidos, y restaurando así un equilibrio. De manera similar, las neuronas subactivas experimentan aumentos de peso neto que las hacen participar y competir de manera más efectiva, y por lo tanto llegan a representar características distintas.

El resultado neto es el desarrollo de un conjunto de detectores neuronales que cubren de manera relativamente uniforme el espacio de diferentes patrones de entradas, con categorías sistemáticas que abarcan las regularidades estadísticas. Por ejemplo, a los gatos les gusta la leche, y a los perros les gustan los huesos, y podemos aprender esto con solo observar la coocurrencia confiable de gatos con leche y perros con huesos. Este tipo de co-ocurrencia confiable es lo que entendemos por “regularidad estadística”. Consulte Hebbian Learning para obtener una ilustración muy simple de por qué los mecanismos de aprendizaje al estilo hebbio capturan patrones de coocurrencia. Realmente es solo una variante de la máxima básica de que “las cosas que disparan juntas, se conectan”.

La tasa de aprendizaje

Hay un factor importante que falta en las ecuaciones anteriores, que es la tasa de aprendizaje; normalmente usamos el épsilon griego\(\epsilon\) para representar este parámetro, que simplemente multiplica la tasa con la que cambian los pesos:

• \(\Delta w=\epsilon f_{x c a l}\left(x y, y_{l}\right)\)

Por lo tanto, un épsilon más grande significa mayores cambios de peso y, por lo tanto, un aprendizaje más rápido, y viceversa para un valor menor. Un valor inicial típico para la tasa de aprendizaje es .04, y a menudo lo hacemos disminuir con el tiempo (lo que también es cierto para el cerebro, los cerebros más jóvenes son mucho más plásticos que los mayores), esto generalmente da como resultado el aprendizaje general más rápido y el mejor rendimiento final.

Muchos investigadores (y compañías farmacéuticas) tienen la creencia potencialmente peligrosa de que una tasa de aprendizaje más rápida es mejor, y se han desarrollado varios medicamentos que efectivamente aumentan la tasa de aprendizaje, haciendo que las ratas aprendan algún tipo de tarea estándar más rápido de lo normal, por ejemplo. No obstante, veremos en el Capítulo de Aprendizaje y Memoria que en realidad una tasa de aprendizaje lenta tiene algunas ventajas muy importantes. Específicamente, una tasa de aprendizaje más lenta permite que el sistema incorpore más estadísticas en el aprendizaje: la tasa de aprendizaje determina la ventana de tiempo efectiva sobre la cual se promedian las experiencias juntas, y una tasa de aprendizaje más lenta proporciona una ventana de tiempo más larga, lo que permite que se integrado. Así, el aprendizaje puede ser mucho más inteligente con una tasa de aprendizaje más lenta. Pero la compensación, por supuesto, es que los resultados de este aprendizaje más inteligente tardan mucho más en impactar el comportamiento real. Muchos han argumentado que los humanos son distintivos en nuestro período extremadamente prolongado de aprendizaje del desarrollo, por lo que podemos aprender mucho antes de que necesitemos comenzar a ganar un cheque de pago. Esto nos permite tener una tasa de aprendizaje bastante lenta, sin demasiadas consecuencias negativas.

Exploración del aprendizaje autoorganizado

La mejor manera de ver esta dinámica es a través de la exploración computacional. Abre la simulación Self Organizing y sigue las indicaciones desde allí.

Aprendizaje impulsado por errores: Umbral flotante de escala de tiempo corto

Aunque el aprendizaje autoorganizado es muy útil, veremos que está significativamente limitado en el tipo de cosas que puede aprender. Es genial para extraer generalidades, pero no tanto a la hora de aprender patrones específicos y complicados. Para aprender estos tipos de problemas más desafiantes, necesitamos un aprendizaje impulsado por errores. Para una discusión más descendente (motivada computacionalmente) sobre cómo lograr un aprendizaje impulsado por errores, y la relación con los mecanismos más motivados biológicamente que consideramos aquí, vea la subsección Backpropagation (que algunos pueden preferir leer primero). Intuitivamente, el aprendizaje impulsado por errores es mucho más poderoso porque impulsa el aprendizaje basado en las diferencias, no en las señales sin procesar. Las diferencias (errores) te dicen con mucha más precisión lo que debes hacer para solucionar un problema. Las señales crudas (patrones generales de actividad neuronal) no son tan informativas: es fácil sentirse abrumado por el bosque y perder de vista los árboles. Veremos ejemplos más específicos más adelante, después de averiguar primero cómo podemos lograr que el aprendizaje impulsado por errores funcione en primer lugar.

Figura\(4.8\): Cómo el umbral flotante en función de la actividad sináptica promedio a medio plazo\(\langle x y\rangle_{m}\) puede producir aprendizaje impulsado por errores. Este marco de tiempo medio refleja el desarrollo de un patrón de actividad neuronal que codifica una expectativa sobre lo que sucederá a continuación. La actividad sináptica a corto plazo más reciente (que impulsa el aprendizaje) representa el resultado real de lo que sucedió después. Debido a la naturaleza (casi) lineal de la función DWt, efectivamente computa la diferencia entre el resultado y la expectativa. Cualitativamente, si el resultado produce una mayor activación de una población de neuronas de lo esperado, los pesos correspondientes suben, mientras que las neuronas que disminuyeron sus estados de actividad como consecuencia del resultado tendrán que bajar sus pesos. Esto se ilustra anteriormente en el caso de expectativas bajas vs altas.

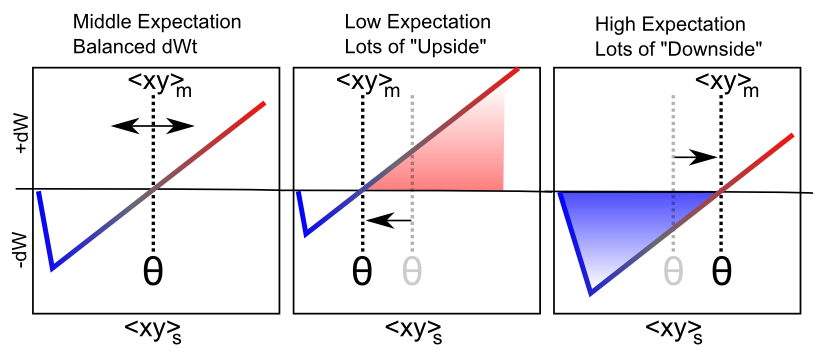
La Figura 4.8 muestra cómo se puede adaptar el mismo comportamiento de umbral flotante desde el aspecto autoorganizativo tipo BCM-del aprendizaje XCAL para realizar un aprendizaje impulsado por errores, en forma de diferencias entre un resultado frente a una expectativa. Específicamente, aceleramos la escala de tiempo para calcular el umbral flotante (y también hacer que refleje la actividad sináptica, no solo la actividad del receptor):

• \(\Theta_{p}=\langle x y\rangle_{m}\)
• \(\Delta w=f_{x c a l}\left(\langle x y\rangle_{s},\langle x y\rangle_{m}\right)=f_{x c a l}\left(x_{s} y_{s}, x_{m} y_{m}\right)\)

donde\(\langle x y\rangle_{m}\) está esta nueva actividad sináptica promedio en escala de tiempo medio, que consideramos refleja una expectativa emergente sobre la situación actual, que se desarrolla a lo largo de aproximadamente 75 ms de actividad neuronal. La actividad neuronal más reciente a corto plazo (últimos 25 ms\(\langle x y\rangle_{s}\)) refleja el resultado real, y es la misma señal basada en calcio que impulsa el aprendizaje en el caso hebbio.

En el simulador, el período de tiempo durante el cual esta expectativa es representada por la red, antes de que llegue a ver el resultado, se conoce como la fase menos (basada en la terminología de la máquina Boltzmann; (Ackley, Hinton, & Sejnowski, 1985)). El período posterior en el que se observa el desenlace (y las activaciones evolucionan para reflejar la influencia de ese desenlace) se conoce como la fase más. Es la diferencia entre esta expectativa y el resultado lo que representa la señal de error en el aprendizaje impulsado por errores (de ahí los términos menos y más — las activaciones de fase menos se restan de las de la fase positiva para impulsar cambios de peso).

Si bien esta comparación expectación-resultado es el requisito fundamental para el aprendizaje impulsado por errores, un cambio de peso basado en esta diferencia por sí mismo plantea la pregunta de cómo las neuronas alguna vez 'sabrían' en qué fase se encuentran. Hemos explorado muchas respuestas posibles a esta pregunta, y la más reciente involucra un ciclo de expectativa de frecuencia alfa generado internamente (periodos de 10 Hz, 100 ms) seguido de desenlace, apoyado por circuitos neocorticales en las capas profundas y el tálamo (O'Reilly, Wyatte, & Rohrlich, 2014; Kachergis, Wyatte, O'Reilly, Kleijn, & Hommel, 2014). Una revisión posterior de este libro de texto lo describirá con más detalle. Por ahora, las principales implicaciones de este marco son organizar los tiempos de procesamiento y aprendizaje de la siguiente manera:

• Un ensayo tiene una duración de 100 mseg (10 Hz, frecuencia alfa) y comprende una secuencia de expectativa: aprendizaje de resultados, organizado en 4 trimestres.

• Biológicamente, las capas neocorticales profundas (capas 5, 6) y el tálamo tienen un ritmo oscilatorio natural a la frecuencia alfa (Buffalo, Fries, Landman, Buschman, & Desimone, 2011; Lorincz, Kekesi, Juhasz, Crunelli, & Hughes, 2009; Franceschetti et al., 1995; Luczak, Bartho, & Harris, 2013). Las dinámicas específicas en estas capas organizan el ciclo de expectativa vs. resultado dentro del ciclo alfa.

• Un trimestre dura 25 mseg (40 Hz, frecuencia gamma) — los primeros 3 trimestres (75 ms) forman la fase expectativa/menos, y el trimestre final es la fase desenlace/plus.

• Biológicamente, las capas neocorticales superficiales (capas 2, 3) tienen una oscilación de frecuencia gamma (Buffalo, Fries, Landman, Buschman, & Desimone, 2011), apoyando la organización de cuarto de nivel.

• Un ciclo representa 1 mseg de procesamiento, donde cada neurona actualiza su potencial de membrana de acuerdo con las ecuaciones cubiertas en el capítulo Neuron.

El mecanismo de aprendizaje XCAL se coordina con este tiempo comparando la actividad sináptica más reciente (predominantemente impulsada por estados de fase plus/resultado) con la integrada a lo largo de la escala de tiempo medio, que efectivamente incluye las fases menos y más. Debido a que la función de aprendizaje XCAL es (mayormente) lineal, la asociación del umbral flotante con esta actividad sináptica en el marco de tiempo medio (incluidos los estados de expectativa), con el que se compara el resultado a corto plazo, calcula directamente su diferencia:

• \(\Delta w \approx x_{s} y_{s}-x_{m} y_{m}\)

Intuitivamente, podemos entender cómo funciona esta regla de aprendizaje impulsada por errores al pensar en diferentes casos específicos. El caso más fácil es cuando la expectativa es equivalente al resultado (es decir, una expectativa correcta) —los dos términos anteriores serán los mismos, y así su resta es cero, y los pesos siguen siendo los mismos. Entonces, una vez que obtienes la perfección, dejas de aprender. ¿Y si tu expectativa fuera mayor que tu resultado? La diferencia será un número negativo, y los pesos disminuirán así, de manera que bajarás tus expectativas la próxima vez. Intuitivamente, esto tiene mucho sentido: si tienes la expectativa de que todas las películas de M. Night Shyamalan van a ser tan geniales como The Sixth Sense, podrías terminar teniendo que reducir tus pesos para alinearte mejor con los resultados reales. Por el contrario, si la expectativa es menor que el resultado, el cambio de peso será positivo, y así aumentar la expectativa. Podrías haber pensado que esta clase iba a ser mortalmente aburrida, pero a lo mejor te divirtió la mención anterior de M. Night Shyamalan, y ahora tendrás que aumentar un poco tus pesos. Es de esperar que quede claro intuitivamente que esta forma de aprendizaje funcionará para minimizar las diferencias entre expectativas y resultados a lo largo del tiempo. Obsérvese que si bien el ejemplo dado aquí se echó en términos de desviaciones de las expectativas que tienen valor (es decir, las cosas resultaron mejor o peor de lo esperado, ya que cubrimos con más detalle en el capítulo Control motor y Aprendizaje por Refuerzo, el mismo principio se aplica cuando los resultados se desvían de otros tipo de expectativas.

Por su naturaleza explícitamente temporal, existen algunas otras formas interesantes de pensar sobre lo que hace esta regla de aprendizaje, además del tiempo explícito definido anteriormente. Para reiterar, la regla dice que el resultado viene inmediatamente después de una expectativa anterior —esto es una consecuencia directa de hacer que aprenda hacia la actividad sináptica promedio a corto plazo (más inmediata), en comparación con un promedio de mediano plazo ligeramente más largo que incluye el tiempo justo antes del presente inmediato.

Figura\(4.9\): Ilustración del principio de aprendizaje atractor contrastivo (CAL), que es la idea central detrás del mecanismo de aprendizaje impulsado por errores XCAL. La red aprende sobre el contraste entre la fase temprana de asentamiento (la fase menos, o promedio de activación de marco de tiempo medio\(\langle x y\rangle_{m}\)) versus la fase tardía de asentamiento (la fase positiva o promedio de activación de marco de tiempo corto\(\langle x y\rangle_{s}\)). La fase tardía ha integrado más de las limitaciones generales en la red y, por lo tanto, representa una “mejor” interpretación o representación general de la situación actual que la fase temprana, por lo que tiene sentido que la fase tardía sirva como la “señal de entrenamiento” en relación con la fase anterior.

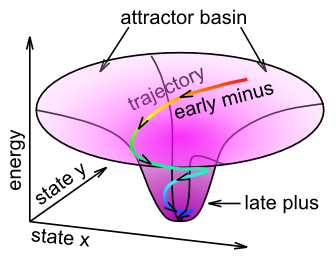
Podemos pensar en este aprendizaje en términos de la dinámica atractora discutida en el Capítulo Redes. Específicamente, el nombre Aprendizaje atractor contrastivo (CAL) refleja la idea de que la red se está instalando en un estado atractor, y es el contraste entre el estado atractor final en el que se asienta la red (es decir, el “resultado” en este caso), versus la trayectoria de activación de la red como se acerca al atractor, que impulsa el aprendizaje (Figura 4.9). El promedio de escala a corto plazo refleja el estado final del atractor (el 'objetivo'), y el promedio de escala de tiempo media refleja toda la trayectoria durante el asentamiento. Cuando el patrón de actividad asociado a la expectativa está lejos del resultado real, la diferencia entre estos dos estados atractores será grande, y el aprendizaje impulsará cambios de peso para que en futuros encuentros, la expectativa refleje más de cerca el resultado (asumiendo que el entorno es confiable). La parte X de XCAL simplemente refleja el hecho de que se logra el mismo objetivo sin tener que comparar explícitamente dos atractores en puntos discretos en el tiempo, sino mediante el uso de un estado de actividad promediado en el tiempo extendido a lo largo de toda la trayectoria de asentamiento como comparación basal, que es más biológicamente realistas porque tales variables son fácilmente accesibles por la actividad neuronal local.

Matemáticamente, esta regla de aprendizaje de CAL representa una versión más simple de la función de aprendizaje oscilante desarrollada por Norman y sus colegas. Consulte Función de aprendizaje oscilante para obtener más detalles.

También hay razones más generales para la información posterior (promedio de escala de tiempo corto) para entrenar información anterior (promedio de escala de tiempo medio). Por lo general, cuanto más tiempo se espera, mejor calidad es la información —al inicio de una oración, es posible que tengas alguna idea de lo que viene después, pero a medida que se despliega, el significado se vuelve cada vez más claro. Esta información posterior puede servir para entrenar las expectativas anteriores, para que puedas entender las cosas de manera más eficiente la próxima vez. En general, estas formas alternativas de pensar sobre el aprendizaje XCAL representan formas de aprendizaje más autoorganizativas sin requerir una señal explícita de entrenamiento de resultados, mientras se usa el contraste más rápido (tiempo corto vs medio) para el mecanismo de aprendizaje impulsado por errores.

Antes de continuar, tal vez se esté preguntando sobre la base biológica de esta forma impulsada por errores del umbral flotante. A diferencia del umbral flotante estilo BCM, que tiene datos empíricos sólidos consistentes con él, la idea de que el umbral cambia en esta escala de tiempo más rápida para reflejar la actividad sináptica promedio de escala de tiempo media aún no se ha probado empíricamente. Así, se erige como una predicción importante de este modelo computacional. Debido a que es tan fácil de calcular, y da como resultado una forma de aprendizaje tan poderosa, parece plausible que el cerebro se aproveche precisamente de tal mecanismo, pero tendremos que ver cómo resiste las pruebas empíricas. Una sugerencia inicial de tal dinámica proviene de este trabajo: Lim et al. (2015), que mostraron una dinámica de aprendizaje similar a la BCM con cambios rápidos en el umbral dependiendo de la actividad reciente. Además, existe evidencia sustancial de que los cambios transitorios en la neuromodulación que ocurren durante eventos sobresalientes e inesperados, son importantes para modificar la plasticidad sináptica, y pueden contribuir funcionalmente a este tipo de mecanismo de aprendizaje impulsado por errores. Además, discutimos un poco más tarde otra preocupación mayor sobre la naturaleza y el origen de la distinción expectativa vs. resultado, que es fundamental para esta forma de aprendizaje impulsado por errores.

Ventajas del aprendizaje basado en errores

Como se señaló anteriormente, el aprendizaje impulsado por errores es mucho más poderoso computacionalmente que el aprendizaje autoorganizado. Por ejemplo, todos los modelos computacionales que funcionan bien ante el difícil desafío de aprender a reconocer objetos en función de su apariencia visual (ver Capítulo Percepción) utilizan una forma de aprendizaje impulsado por errores. Muchos también usan el aprendizaje autoorganizado, pero esto tiende a desempeñar un papel más de apoyo, mientras que los modelos serían completamente infuncionales sin un aprendizaje impulsado por errores. El aprendizaje impulsado por errores asegura que el modelo haga que los tipos de discriminaciones categóricas sean relevantes, al tiempo que evita las que son irrelevantes. Por ejemplo, si una vista lateral de un automóvil está orientada hacia la izquierda o hacia la derecha no es relevante para determinar que se trata de un automóvil. Pero la presencia de ruedas es muy importante para discriminar un automóvil de un pez. Un modelo puramente autoorganizado no tiene forma de saber que estas diferencias, que pueden ser señales bastante confiables estadísticamente y fuertes en la entrada, difieren en su utilidad para las categorías que le importan a las personas.

Matemáticamente, la historia de las funciones de aprendizaje impulsadas por errores proporciona una ventana fascinante a la sociología de la ciencia, y cómo las ideas aparentemente simples pueden tardar un tiempo en desarrollarse. En la subsección Backpropagation, trazamos esta historia a través de la derivación de reglas de aprendizaje impulsadas por errores, desde la regla delta (desarrollada por Widrow y Hoff en 1960) hasta la regla de aprendizaje de retropropagación muy ampliamente utilizada (Rumelhart et al., 1986). Al inicio de esa subsección, mostramos cómo la forma XCAL de aprendizaje impulsado por errores (específicamente la versión CAL del mismo) puede derivarse directamente de la retropropagación, proporcionando así una cuenta matemáticamente satisfactoria de por qué es capaz de resolver tantos problemas difíciles.

La idea clave detrás de la función de aprendizaje de retropropagación es que las señales de error que surgen en una capa de salida pueden propagarse hacia atrás a capas ocultas anteriores para impulsar el aprendizaje en estas capas anteriores de modo que resuelva el problema general que enfrenta la red (es decir, asegurará que el red puede producir las expectativas o respuestas correctas en la capa de salida). Esto es esencial para permitir que el sistema en su conjunto resuelva problemas difíciles —como discutimos en el Capítulo de Redes, mucha inteligencia surge de múltiples capas de pasos de categorización en cascada— para que todos estos pasos intermedios se centren en las categorías relevantes, error las señales necesitan propagarse a través de estas capas y dar forma al aprendizaje en todas ellas.

Figura\(4.10\): Intuición de cómo las conexiones bidireccionales permiten la retropropagación de señales de aprendizaje de otras partes de la red, cuando hay una diferencia entre una expectativa y un resultado en cualquier parte de la red, las neuronas en otras partes de la red “sienten” esa diferencia a través de la conexión bidireccional. Todas las neuronas experimentan un impacto en su propia activación tanto de la expectativa como del resultado, y así cuando aprenden sobre la diferencia entre estos dos puntos en el tiempo (luego entrenando antes), están aprendiendo sobre su propio impacto en el resultado: error de expectativa, y cambios de peso basados en esto la diferencia terminará minimizando el error general en la red en su conjunto. Las neuronas más cercanas a la fuente del error aprenden más, con el error disminuyendo con la distancia de esta fuente.

Biológicamente, la conectividad bidireccional en nuestros modelos permite que estas señales de error se propaguen de esta manera (Figura 4.10). Así, los cambios en cualquier ubicación dada en la red irradian hacia atrás (y en cada dirección van las conexiones) para afectar los estados de activación en todas las demás capas, a través de la conectividad bidireccional, y esto influye entonces en el aprendizaje en estas otras capas. En otras palabras, XCAL utiliza dinámicas de activación bidireccional para comunicar señales de error a través de la red, mientras que la retropropagación utiliza un procedimiento biológicamente inverosímil que propaga señales de error hacia atrás a través de conexiones sinápticas, en la dirección opuesta a la forma en que la activación típicamente fluye. Además, la red XCAL experimenta una secuencia de estados de activación, pasando de una expectativa a experimentar un resultado posterior, y aprende sobre la diferencia entre estos dos estados. Por el contrario, la retropropagación calcula un único valor delta de error que es efectivamente la diferencia entre el resultado y la expectativa, y luego envía este valor único hacia atrás a través de las conexiones. Consulte la subsección Backpropagation para saber cómo estas dos cosas diferentes pueden ser matemáticamente equivalentes. Además, es una buena idea mirar la discusión del proceso de asignación de crédito en esta subsección, para obtener una comprensión más completa de cómo funciona el aprendizaje impulsado por errores.

Exploración del aprendizaje impulsado por errores

La simulación de Pattern Associator proporciona una buena demostración de las limitaciones del aprendizaje autoorganizado al estilo Hebbian, y cómo el aprendizaje impulsado por errores supera estas limitaciones, en el contexto de un simple asociador de patrones de dos capas que aprende asignaciones básicas de entrada/salida. Siga las instrucciones en ese enlace de simulación para ejecutar la exploración.

Deberías haber visto que una de las tareas de mapeo de entrada/salida era imposible para resolver incluso el aprendizaje impulsado por errores, en la red de dos capas. La siguiente exploración, Error Driven Hidden muestra que la adición de una capa oculta, combinada con el poderoso mecanismo de aprendizaje impulsado por errores, permite que incluso este problema “imposible” se resuelva ahora. Esto demuestra el poder computacional del algoritmo de Backpropagation.

Aprendizaje combinado autoorganizado e impulsado por errores

Aunque los científicos tienden a querer elegir lados con fuerza y declarar que el aprendizaje autoorganizado o el aprendizaje impulsado por errores es la mejor manera de hacerlo, en realidad hay muchas ventajas en combinar ambas formas de aprendizaje juntas. Cada forma de aprendizaje tiene fortalezas y debilidades complementarias:

• La autoorganización es más robusta, porque solo depende de las estadísticas locales de disparo, mientras que el aprendizaje impulsado por errores depende implícitamente de señales de error provenientes de áreas potencialmente distantes. La autoorganización puede lograr algo útil incluso cuando las señales de error son remotas o aún no son muy coherentes.
• Pero el aprendizaje autoorganizado también es muy miope —no se coordina con el aprendizaje en otras capas, y por lo tanto tiende a ser “codicioso”. Por el contrario, el aprendizaje impulsado por errores logra esta coordinación y puede aprender a resolver problemas que requieren la acción colectiva de múltiples unidades a través de múltiples capas.

Una analogía que puede resultar útil es que el aprendizaje impulsado por errores es como la política de izquierda; requiere que todas las diferentes capas y unidades trabajen juntas para lograr objetivos comunes, mientras que el aprendizaje autoorganizado es como la política de derecha, enfatizando acciones locales y codiciosas que de alguna manera también benefician la sociedad en su conjunto, sin coordinarse explícitamente con los demás. Las compensaciones de estos enfoques políticos son similares a las de las respectivas formas de aprendizaje. Los enfoques socialistas pueden dejar a las personas individuales sintiéndose poco motivadas, ya que son solo un pequeño engranaje en una enorme máquina sin rostro. De igual manera, las neuronas que dependen estrictamente del aprendizaje impulsado por errores pueden terminar no aprendiendo mucho, ya que solo necesitan hacer una contribución muy pequeña y algo “anónima” para resolver el problema general. Una vez eliminadas las señales de error (es decir, las expectativas coinciden con los resultados), el aprendizaje se detiene. Veremos que las redes que dependen del aprendizaje puro impulsado por errores a menudo tienen pesos de aspecto muy aleatorio, lo que refleja este mínimo de esfuerzo dedicado a resolver el problema general. Por otro lado, los enfoques capitalistas de derecha más fuertemente pueden terminar con bucles de retroalimentación positiva excesivos (los ricos se vuelven cada vez más ricos) y, por lo general, no son buenos para lidiar con problemas de mayor escala y a largo plazo que requieren coordinación y planificación. Del mismo modo, los modelos puramente autoorganizados tienden a terminar con distribuciones más desiguales de “riqueza representacional” y casi nunca terminan resolviendo problemas desafiantes, prefiriendo en cambio codificar con avidez cualquier estadística interesante que se les presente. Curiosamente, nuestros modelos sugieren que un equilibrio de ambos enfoques —un enfoque centrista — ¡parece funcionar mejor! Quizás esta lección pueda generalizarse de nuevo a la arena política.

Dejando a un lado las analogías coloridas, la mecánica real de combinar ambas formas de aprendizaje dentro del marco XCAL equivale a fusionar las dos definiciones diferentes del valor umbral flotante. Biológicamente, pensamos que existe un promedio ponderado combinado de los dos umbrales, utilizando un parámetro “lambda” para ponderar el promedio receptor\(\lambda\) a largo plazo (autoorganizado) en relación con el coproducto sináptico a mediano plazo:

• \(\theta_{p}=\lambda y_{l}+(1-\lambda) x_{m} y_{m}\)

Sin embargo, computacionalmente, es más claro y sencillo simplemente combinar funciones XCAL separadas, cada una con su propia función de ponderación, debido a la linealidad de la función, esto es matemáticamente equivalente:

• \(\Delta w=\lambda_{f} f_{x c a l}\left(x_{s} y_{s}, y_{l}\right)+\lambda_{m} f_{x c a l}\left(x_{s} y_{s}, x_{m} y_{m}\right)\)

Es razonable que estos parámetros lambda puedan diferir según el área cerebral (es decir, algunos sistemas cerebrales aprenden más sobre las regularidades estadísticas, mientras que otros están más enfocados en minimizar el error), e incluso que puede ser regulado dinámicamente (es decir, cambios transitorios en neuromoduladores como dopamina y acetilcolina puede influir en el grado en que se enfatizan las señales de error).

Hay pequeñas pero confiables ventajas computacionales para automatizar este equilibrio de aprendizaje autoorganizado vs. aprendizaje impulsado por errores (es decir, un\(\lambda_{l}\) valor calculado dinámicamente, mientras se mantiene\(\lambda_{m}=1\)), basado en dos factores: la magnitud de la activación promedio de ejecución de la unidad receptora y_l, y el promedio magnitud de las señales de error presentes en una capa (ver Detalles de Leabra).

Fijación de peso y mejora del contraste

El último tema que debemos abordar computacionalmente es el problema de los pesos sinápticos que crecen sin ataduras. En los experimentos de LTP, está claro que hay un valor máximo de peso sináptico — no se puede seguir obteniendo LTP en la misma sinapsis al conducirla una y otra vez. El valor de peso satura. Hay un límite natural en el extremo inferior, para LTD, de cero. Matemáticamente, la forma más sencilla de lograr este tipo de límite de peso es a través de una función de enfoque exponencial, donde los cambios de peso se vuelven exponencialmente más pequeños a medida que se acercan los límites. Esta función se expresa más directamente en un formato de lenguaje de programación, ya que implica un condicional:

si dwt > 0 entonces wt = wt + (1 - wt) * dwt; de
lo contrario wt = wt + wt * dwt;

En palabras: si se supone que los pesos aumentan (dwt es positivo), entonces multiplique la tasa de aumento por 1-wt, donde 1 es el límite superior, y de lo contrario, multiplique por el propio valor de peso. A medida que el peso se acerca a 1, los aumentos de peso se hacen cada vez más pequeños, y de manera similar a medida que el valor de peso

La función de enfoque exponencial funciona bien para mantener los pesos acotados de manera gradual (mucho mejor que simplemente recortar los valores de peso en los límites, lo que pierde toda la señal para pesos saturados), pero también crea una fuerte tendencia a que los pesos pasen el rato en el medio del rango, alrededor de .5. Esto crea problemas porque entonces las neuronas no tienen respuestas suficientemente distintas a diferentes patrones de entrada, y luego la competencia inhibitoria se descompone (muchas neuronas se activan débilmente), lo que luego interfiere con el bucle de retroalimentación positiva que es esencial para el aprendizaje, etc. Para contrarrestar estos problemas, manteniendo el límite exponencial, introducimos una función de mejora de contraste en los pesos:

• \(\hat{w}=\frac{1}{1+\left(\frac{w}{\theta(1-w)}\right)^{-\gamma}}\)

Como puede ver en la Figura 4.11, esta función crea un mayor contraste para los valores de peso alrededor de este valor central de .5: se empujan hacia arriba o hacia abajo hasta los extremos. Este valor de peso con contraste mejorado se usa luego para la comunicación entre las neuronas, y es lo que se muestra como el valor wt en el simulador.

Figura\(4.11\): Función de mejora de contraste de peso, ganancia (gamma) = 6, desplazamiento (theta) = 1.25.

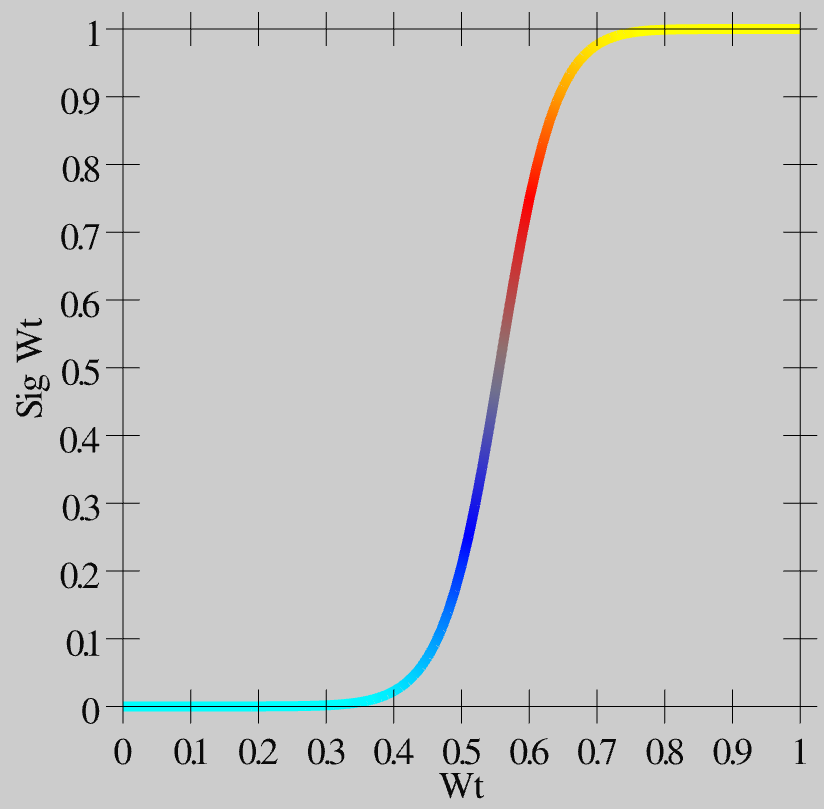
Biológicamente, pensamos en el valor de peso simple w, que está involucrado en las funciones de aprendizaje, como una variable interna que rastrea con precisión las estadísticas de las funciones de aprendizaje, mientras que el valor de peso con contraste mejorado es el valor de eficacia sináptica real que mide y observa como el fuerza de interacción entre neuronas. Así, el valor de w simple puede corresponder al estado de fosforilación de CAMKII o algún otro valor interno apropiado que media la plasticidad sináptica.

Por último, consulte Detalles Implementacionales para algunos detalles implementacionales sobre la forma en que se calculan los promedios de tiempo, los cuales no afectan nada conceptualmente, pero si realmente quiere saber exactamente qué está pasando..