7.3: Dopamina y Aprendizaje por Refuerzo de Diferencia Temporal

Figura\(7.5\): Patrones característicos de disparo neural de las neuronas dopaminérgicas en el área tegmental ventral (VTA) y sustancia negra pars compacta (SnC), en una sencilla tarea de acondicionamiento. Antes del acondicionamiento, cuando se entrega una recompensa, las neuronas de dopamina disparan una explosión de actividad (panel superior — el histograma en la parte superior muestra la suma de picos neuronales a través de las trazas de grabación repetidas que se muestran a continuación, siendo cada fila un ensayo de grabación diferente). Después de que el animal haya aprendido a asociar un estímulo condicionado (CS) (por ejemplo, un tono) con la recompensa, las neuronas de dopamina ahora disparan al inicio del CS, y no a la recompensa misma. Si se retiene una recompensa después del CS, hay una caída o pausa en el disparo de dopamina, lo que indica que hubo algún tipo de predicción de la recompensa, y cuando no llegó, hubo un error de predicción negativo. Este patrón general de disparo en todas las condiciones es altamente consistente con los modelos de aprendizaje de refuerzo basados en el error de predicción de recompensa.

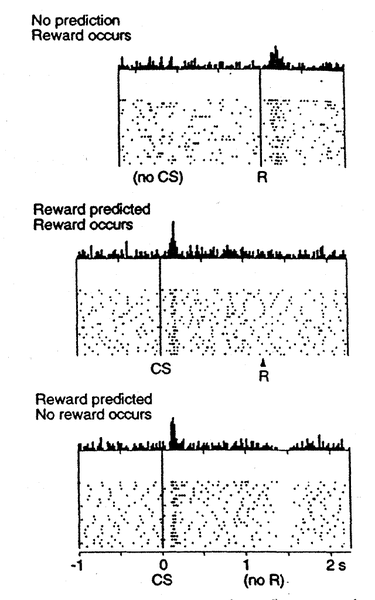
Si bien consideramos anteriormente cómo los cambios fásicos en la dopamina pueden impulsar a Go y NoGo a aprender a seleccionar las acciones más gratificantes y evitar las menos gratificantes, no hemos abordado anteriormente cómo las neuronas de la dopamina llegan a representar estas señales fásicas para impulsar el aprendizaje. Uno de los descubrimientos más emocionantes de los últimos años fue el hallazgo de que las neuronas dopaminéricas en el área tegmental ventral (VTA) y la sustancia negra pars compacta (SnC) se comportan de acuerdo con modelos de aprendizaje de refuerzo basados en el error de predicción de recompensa. A diferencia de algunos conceptos erróneos populares, estas neuronas de dopamina no codifican directamente el valor de recompensa en bruto. En cambio, codifican la diferencia entre la recompensa recibida versus una expectativa de recompensa. Esto se muestra en la Figura 7.5: si no hay expectativa de recompensa, entonces las neuronas de dopamina disparan a la recompensa, reflejando un error de predicción de recompensa positivo (expectativa cero, recompensa positiva). Si un estímulo condicionado (CS, por ejemplo, un tono o luz) predice de manera confiable una recompensa posterior, entonces las neuronas ya no disparan a la recompensa misma, reflejando la falta de error de predicción de recompensa (expectativa = recompensa). En cambio, las neuronas de dopamina disparan hasta el inicio del CS. Si la recompensa se omite siguiendo el CS, entonces las neuronas de dopamina realmente van por otro lado (una “caída” o “pausa” en el nivel tónico bajo de disparo de neuronas dopamina), reflejando un error de predicción de recompensa negativo (predicción de recompensa positiva, recompensa cero).

Computacionalmente, el modelo más simple de error de predicción de recompensa es el modelo de acondicionamiento Rescorla-Wagner, que es matemáticamente idéntico a la regla delta como se discute en el capítulo Mecanismos de Aprendizaje, y es simplemente la diferencia entre la recompensa real y la recompensa esperada:

• \(\delta=r-\hat{r}\)
• \(\delta=r-\sum x w\)

donde\(\delta\) (“delta”) es el error de predicción de recompensa, r es la cantidad de recompensa realmente recibida, y\(\hat{r}=\sum x w\) es la cantidad de recompensa esperada, que se calcula como una suma ponderada sobre estímulos de entrada\(x\) con pesos\(w\). Los pesos se adaptan para tratar de predecir con precisión los valores reales de recompensa, y de hecho este valor delta especifica la dirección en la que deben cambiar los pesos:

• \(\Delta w=\delta x\)

Esto es idéntico a la regla de aprendizaje delta, incluida la importante dependencia de la actividad de estímulo\(x\); solo se quieren cambiar los pesos de los estímulos que realmente están presentes (es decir, los distintos\(x\) de cero).

Cuando la predicción de recompensa es correcta, entonces el valor real de recompensa es cancelado por la predicción, como se muestra en el segundo panel de la Figura 7.5. Esta regla también predice con precisión los otros casos que se muestran en la figura también (errores de predicción de recompensa positivos y negativos).

Lo que el modelo Rescorla-Wagner no logra capturar es el disparo de dopamina hasta el inicio del CS en el segundo panel de la Figura 7.5. Sin embargo, un modelo ligeramente más complejo conocido como la regla de aprendizaje de diferencias temporales (TD) captura este disparo de inicio CS, al introducir el tiempo en la ecuación (como su nombre indica). En relación con Rescorla-Wagner, TD solo agrega un término adicional a la ecuación delta, que representa los valores de recompensa futuros que podrían llegar más tarde en el tiempo:

• \(\delta=(r+f)-\hat{r}\)

donde\(f\) representa las recompensas futuras, y ahora la expectativa de recompensa\(\hat{r}=\sum x w\) tiene que tratar de anticipar tanto la recompensa\(r\) actual como esta recompensa futura\(f\). En una tarea de acondicionamiento simple, donde el CS predice de manera confiable una recompensa posterior, el inicio de la CS da como resultado un aumento en este\(f\) valor, porque una vez que llega el CS, hay una alta probabilidad de recompensa en el futuro cercano. Además, esto\(f\) en sí mismo no es predecible, porque el inicio del CS no es predicho por ninguna señal anterior (y si lo fuera, entonces esa señal anterior sería la CS real, e impulsaría la ráfaga de dopamina). Por lo tanto, la\(\hat{r}\) expectativa no puede cancelar el\(f\) valor, y se produce una explosión de dopamina.

Aunque este\(f\) valor explica el disparo de dopamina de inicio de CS, plantea la pregunta de ¿cómo puede el sistema saber qué tipo de recompensas vienen en el futuro? Como cualquier cosa que tenga que ver con el futuro, fundamentalmente solo tienes que adivinar, usando el pasado como tu guía lo mejor posible. TD hace esto tratando de hacer cumplir la consistencia en las estimaciones de recompensas a lo largo del tiempo. En efecto, la estimación en el tiempo\(t\) se utiliza para entrenar la estimación a tiempo\(t-1\), y así sucesivamente, para mantener todo lo más consistente posible a lo largo del tiempo, y consistente con las recompensas reales que se reciben a lo largo del tiempo.

Todo esto se puede derivar de una manera muy satisfactoria especificando algo conocido como función de valor, V (t) que es una suma de todas las recompensas presentes y futuras, con las recompensas futuras descontadas por un factor “gamma”, que captura la noción intuitiva que recompensa más en el futuro valen menos que los que ocurrirán antes. Como dice el personaje de Wimpy en Popeye, “con mucho gusto te pagaré hoy el martes por una hamburguesa”. Aquí está esa función de valor, que es una suma infinita que va hacia el futuro:

• \(V(t)=r(t)+\gamma^{1} r(t+1)+\gamma^{2} r(t+2) \ldots\)

Podemos deshacernos del infinito escribiendo esta ecuación recursivamente:

• \(V(t)=r(t)+\gamma V(t+1)\)

Y como no sabemos nada con certeza, todos estos términos de valor son realmente estimaciones, denotadas por los pequeños “sombreros” por encima de ellos:

• \(\hat{V}(t)=r(t)+\gamma \hat{V}(t+1)\)

Entonces esta ecuación nos dice cuál\(t\) debería ser nuestra estimación en el momento actual, en términos de la estimación futura en el momento\(t+1\). A continuación, restamos\(\hat{V}\) de ambos lados, lo que nos da una expresión que es otra forma de expresar la igualdad anterior —que la diferencia entre estos términos debe ser igual a cero:

• \(0=(r(t)+\hat{V}(t+1))-\hat{V}(t)\)

Esto es afirmar matemáticamente el punto en el que TD intenta mantener las estimaciones consistentes a lo largo del tiempo — su diferencia debería ser cero. Pero a medida que estamos aprendiendo nuestras\(\hat{V}\) estimaciones, esta diferencia no será cero, y de hecho, la medida en que no sea cero es la medida en que hay un error de predicción de recompensa:

• \(\delta=(r(t)+\hat{V}(t+1))-\hat{V}(t)\)

Si comparas esto con la ecuación con\(f\) en ella anterior, puedes ver que:

• \(f=\gamma \hat{V}(t+1)\)

y de lo contrario todo lo demás es igual, excepto que hemos aclarado la dependencia temporal de todas las variables, y nuestra expectativa de recompensa es ahora una “expectativa de valor” en su lugar (reemplazando el\(\hat{r}\) por a\(\hat{V}\)). Además, al igual que con Rescorla-Wagner, el valor delta aquí impulsa el aprendizaje de las expectativas de valor.

La regla de aprendizaje TD se puede utilizar para explicar una gran cantidad de diferentes fenómenos de condicionamiento, y su ajuste con el disparo de neuronas de dopamina en el cerebro ha llevado a una gran cantidad de avances en la investigación. Representa un verdadero triunfo del enfoque de modelado computacional para comprender (y predecir) la función cerebral.

Exploración del aprendizaje TD

RL abierto para una exploración del aprendizaje por refuerzo basado en TD en paradigmas de condicionamiento simple. Esta exploración debería ayudar a solidificar su comprensión del aprendizaje por refuerzo, el error de predicción de recompensas y el condicionamiento clásico simple.

La arquitectura actor-crítica para el aprendizaje motor

Figura\(7.6\): Estructura básica de la arquitectura crítica del actor para el control motor. El crítico se encarga de procesar las entradas de recompensa (\(r\)), convirtiéndolas en errores de predicción de recompensas (\(\delta\)), que son adecuados para impulsar el aprendizaje tanto en el crítico como en el actor. El actor es responsable de producir la salida del motor dada la entrada sensorial relevante, y no procesa las expectativas de recompensa o recompensa directamente. Esta es una división eficiente del trabajo, y es esencial para aprender a transformar las recompensas en errores de predicción de recompensas, de lo contrario el sistema sobreaprendería en tareas simples que dominó hace mucho tiempo.

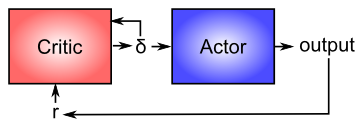
Ahora que se tiene una mejor idea de cómo funciona la dopamina, podemos reconsiderar su papel en la modulación del aprendizaje en los ganglios basales (como se muestra en la Figura 7.4). Desde una perspectiva computacional, la idea clave es la distinción entre un actor y un crítico (Figura 7.6), donde se asume que las recompensas resultan al menos en parte del correcto desempeño del actor. El ganglio basal es el actor en este caso, y la señal de dopamina es la salida del crítico, que luego sirve como señal de entrenamiento para el actor (y también para el crítico como vimos antes). La señal de error de predicción de recompensa producida por el sistema de dopamina es una buena señal de entrenamiento porque impulsa un aprendizaje más fuerte al principio de un proceso de adquisición de habilidades, cuando las recompensas son más impredecibles, y reduce el aprendizaje a medida que se perfecciona la habilidad, y las recompensas son, por lo tanto, más Si el sistema aprendiera directamente sobre la base de recompensas externas, continuaría aprendiendo sobre habilidades que durante mucho tiempo se han dominado, y esto probablemente conduciría a una serie de malas consecuencias (pesos sinápticos cada vez más fuertes, interferencia con otros aprendizajes más nuevos, etc.).

Figura\(7.7\): El esquema de aprendizaje del actor oponente (OpAl). Se trata de un crítico de actor modificado por el cual el actor contiene pesos G y N separados que representan las vías Go y NoGO. Las actividades de las vías son escaladas por los niveles de dopamina durante la elección, y las diferencias relativas de activación para cada acción se comparan para hacer una elección. La figura representa la selección entre tres acciones que tienen diferentes costos y beneficios aprendidos (piense en café, té, agua: claramente el café tiene un mejor beneficio que el té, pero también tiene costos más altos (nerviosismo, etc)). Cuando los niveles de dopamina son bajos (izquierda), los costos se amplifican y los beneficios disminuyen, y el sistema elige evitar el mayor costo y selecciona la acción 3 (agua). Cuando los niveles de dopamina son altos, los beneficios se amplifican y los costos disminuyen, y elige la acción 1 (café). Los niveles moderados de dopamina están asociados con la acción 2 (té; no se muestra). Esto explica los efectos diferenciales de la dopamina en el aprendizaje y la elección entre acciones con diferentes costos y beneficios. De Collins & Frank, 2014.

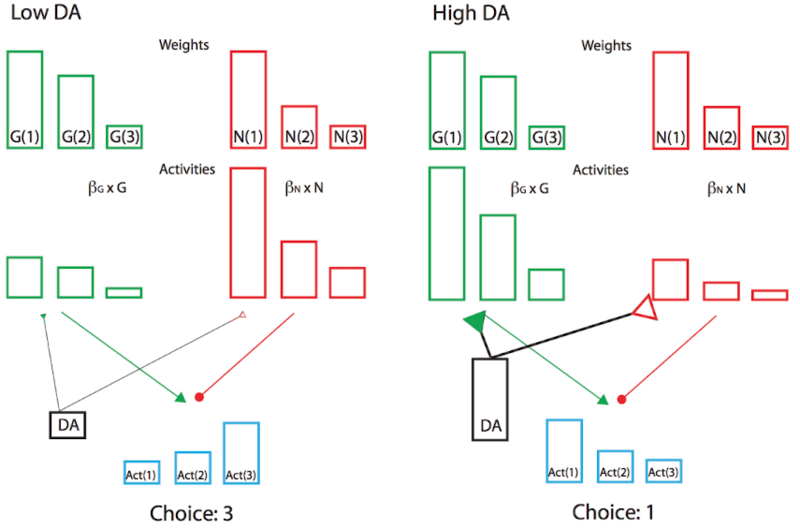
Además, el signo del error de predicción de recompensa es apropiado para los efectos de la dopamina en las vías Go y NoGO en el cuerpo estriado, como vimos en el proyecto del modelo BG anterior. Los errores positivos de predicción de recompensas, cuando se reciben recompensas inesperadas, indican que la acción seleccionada fue mejor de lo esperado, y así ir disparando para esa acción debería aumentarse en el futuro. El aumento de la activación producida por la dopamina en estas neuronas Go tendrá este efecto, asumiendo que el aprendizaje es impulsado por estos niveles de activación. Por el contrario, los errores negativos de predicción de recompensa facilitarán el disparo de NoGo, haciendo que el sistema evite esa acción en el futuro. De hecho, el complejo modelo de red neuronal de los circuitos BG Go/Nogo puede simplificarse con un análisis más formal en una arquitectura actor-crítico modificada llamada Opositor Actor Learning (OpAl; Figura 7.7), donde el actor se divide en pesos contrincantes G y N independientes, y donde su contribución relativa es afectada por los niveles de dopamina tanto durante el aprendizaje como en la elección (Collins & Frank 2014).

Finalmente, la capacidad de la señal de dopamina para propagarse hacia atrás en el tiempo es crítica para cubrir los inevitables retrasos entre las acciones motoras y las recompensas posteriores. Específicamente, la respuesta a la dopamina debe pasar del momento de la recompensa al momento de la acción que predice de manera confiable la recompensa, de la misma manera que se mueve en el tiempo hasta el inicio de la CS en un paradigma de condicionamiento clásico.

El modelo PVLV de DA Biology

Figura\(7.8\): Mapeo biológico del algoritmo PVLV, el cual tiene dos subsistemas separados: Valor Primario (PV) y Valor Aprendido (LV). Cada subsistema tiene subcomponentes excitadores e inhibidores, llamados así por su efecto sobre el disparo de dopamina. \(P V_{e}\)= recompensas primarias que excitan dopamina, asociadas con núcleo hipotalámico lateral (LHA). \(P V_{i}\)= cancelación inhibitoria del disparo de dopamina a recompensas, impulsado por neuronas tipo parche en el estriado ventral (VS_patch). \(L V_{e}\)= impulso excitatorio del núcleo central de la amígdala (CNA), que representa CS. \(L V_{i}\)= cancelación inhibitoria de la\(L V_{e}\) excitación, también a través de neuronas tipo parche en el estriado ventral. El núcleo tegmental pedunculopontino (PPTN) puede transformar entradas sostenidas en respuestas fásicas de dopamina a través de una operación delta temporal simple.

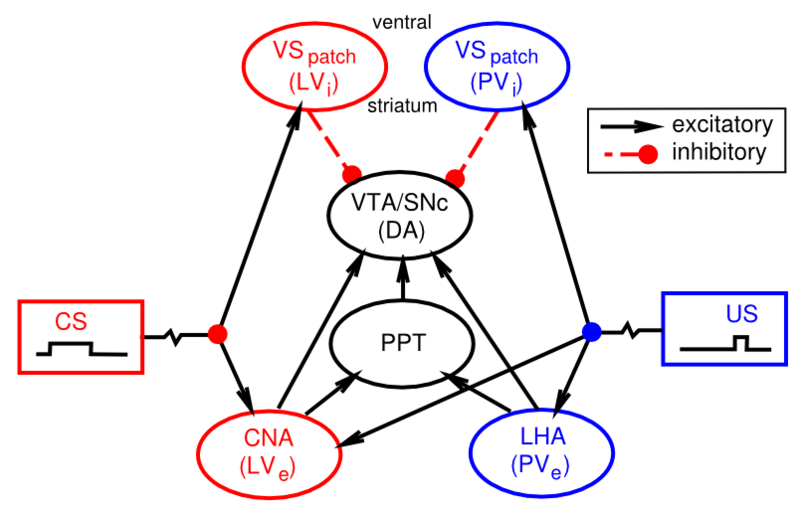
Te habrás dado cuenta de que aún no hemos explicado a nivel biológico cómo las neuronas de dopamina en el VTA y Snc realmente llegan a exhibir su disparo de error de predicción de recompensa. Existe un creciente cuerpo de datos que apoyan la afectación de las áreas cerebrales que se muestran en la Figura 7.8:

• El hipotálamo lateral (LHA) proporciona una señal de recompensa primaria para recompensas básicas como comida, agua, etc.
• Las neuronas tipo parche en el cuerpo estriado ventral (VS-parche) tienen conexiones inhibitorias directas sobre las neuronas dopamina en el VTA y el SNc, y probablemente juegan el papel de cancelar la influencia de las señales de recompensa primaria cuando estas recompensas se han predicho con éxito.
• El núcleo central de la amígdala (CNA) es importante para impulsar el disparo de dopamina a la aparición de estímulos condicionados. Recibe ampliamente de la corteza, y se proyecta directa e indirectamente hacia el VTA y el SnC. Las neuronas en el CNA exhiben disparo relacionado con CS.

Figura\(7.9\): Cómo los diferentes componentes del PVLV contribuyen al patrón general de disparo de dopamina en un paradigma de acondicionamiento simple. Al inicio del CS,\(L V_{e}\) responde con estallido excitatorio de dopamina, debido al aprendizaje previo en el momento de la recompensa externa (\(P V_{e}\)), lo que asoció el CS con el\(L V_{e}\) sistema (en el ANC). Cuando entra la recompensa externa (estímulo incondicionado o Estados Unidos), el\(P V_{i}\) sistema cancela parcialmente la excitación de\(P V_{e}\), con el tiempo, el aprendizaje\(P V_{i}\) entra a cancelarlo por completo.

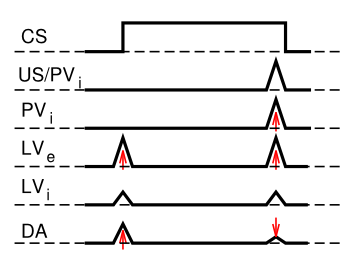
Dado que hay distintas áreas cerebrales involucradas en estos diferentes aspectos del disparo de dopamina, plantea la pregunta de cómo el algoritmo de aprendizaje TD aparentemente unificado podría implementarse en áreas tan diferentes del cerebro. En respuesta a esta pregunta básica, se desarrolló el modelo PVLV de disparo de dopamina. PVLV significa Valor primario, Valor aprendido, y la idea clave es que diferentes estructuras cerebrales están involucradas en el momento en que se experimentan valores primarios, versus cuando se experimentan estímulos condicionados (valores aprendidos). Esto requiere entonces una formulación matemática diferente, en comparación con TD.

La señal de dopamina en PVLV para valores primarios (PV), que está vigente en el momento en que se entregan o se esperan recompensas externas, es idéntica a Rescorla-Wagner, solo usando diferentes etiquetas para las variables:

• \(\delta_{p v}=r-\hat{r}\)
• \(\delta_{p v}=P V_{e}-P V_{i}\)

Donde los subíndices excitatorio (\(e\)\(i\)) e inhibitorio () denotan los dos componentes del sistema de valores primarios, y el signo de su influencia en el disparo de dopamina.

La señal de dopamina para valores aprendidos (LV) se aplica siempre que PV no (es decir, cuando las recompensas externas no están presentes o esperadas), y tiene una forma similar:

• \(\delta_{l v}=L V_{e}-L V_{i}\)

Dónde\(L V_{e}\) está el impulso excitatorio sobre la dopamina del CNA, que aprende a responder a los CS. \(L V_{i}\)es un impulso inhibitorio contrarrestante, nuevamente pensado que está asociado con las neuronas tipo parche del estriado ventral. Aprende mucho más lentamente que el\(L V_{e}\) sistema, y eventualmente aprenderá a cancelar las respuestas de dopamina asociadas a CS, una vez que estos CS se vuelven altamente familiares (más allá de la corta escala de tiempo de la mayoría de los experimentos).

Los\(P V_{i}\) valores se aprenden de la misma manera que en la regla delta o Rescorla-Wagner, y los\(L V_{i}\) valores\(L V_{e}\) y también se aprenden de manera similar, excepto que su señal de entrenamiento es impulsada directamente de los valores de\(P V_{e}\) recompensa, y solo ocurre cuando recompensas externas están presentes o esperados. Esto es crítico\(L V_{e}\) para permitir, por ejemplo, activarse en el momento del inicio de CS, cuando no hay ningún valor de recompensa real presente. Si siempre\(L V_{e}\) estaba aprendiendo a igualar el valor actual de\(P V_{e}\), entonces esta ausencia de\(P V_{e}\) valor al inicio del CS eliminaría rápidamente la\(L V_{e}\) respuesta entonces. Consulte Aprendizaje PVLV para conocer el conjunto completo de ecuaciones que rigen el aprendizaje de los componentes LV y PV.

Hay una serie de propiedades interesantes de las limitaciones de aprendizaje en el sistema PVLV. En primer lugar, el CS debe seguir activo al momento de la recompensa externa para que el\(L V_{e}\) sistema pueda enterarse de ella, ya que LV solo aprende en el momento de la recompensa externa. Si el propio CS se apaga, entonces se debe sostener algún recuerdo de ella. Esto encaja bien con las restricciones conocidas en el aprendizaje de CS en paradigmas de condicionamiento. En segundo lugar, la explosión de dopamina en el momento del inicio de la CS no puede influir en el aprendizaje en el propio sistema del VI; de lo contrario, habría un bucle de retroalimentación positiva sin verificar. Una implicación de esto es que el sistema LV no puede soportar el acondicionamiento de segundo orden, donde un primer CS predice un segundo CS que luego predice la recompensa. Consistente con esta restricción, el CNA (i.e.,\(L V_{e}\)) parece estar involucrado solo en el acondicionamiento de primer orden, mientras que el núcleo basolateral de la amígdala (BLA) es necesario para el acondicionamiento de segundo orden. Además, no parece haber mucha evidencia de terceros o superiores órdenes de condicionamiento. Finalmente, hay una gran cantidad de datos específicos sobre las diferencias en el aprendizaje asociado a CS vs Estados Unidos que son consistentes con el marco PVLV (ver Hazy et al, 2010 para una revisión exhaustiva).

En resumen, el sistema PVLV puede explicar cómo los diferentes sistemas biológicos están involucrados en la generación de respuestas fásicas de dopamina en función de asociaciones de recompensa, de una manera que parece encajar con restricciones por lo demás algo peculiares en el sistema. Además, veremos en el Capítulo de Función Ejecutiva que el PVLV proporciona una señal de aprendizaje más limpia para controlar el papel de los ganglios basales en el sistema de memoria de trabajo de la corteza prefrontal.

Exploración de PVLV

• Modelo PVLV de los mismos casos de acondicionamiento simples explorados en el modelo TD: PVLV