8.2: Unidad 2: Ejes programables CNC para Máquina Herramienta y Sistemas de Dimensionamiento de Posición
- Page ID
- 153549
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)OBJETIVO
Después de completar esta unidad, deberías ser capaz de:
- Comprender el sistema de coordenadas cartesianas.
- Entender las coordenadas cartesianas del avión.
- Comprender las coordenadas cartesianas del espacio tridimensional.
- Entender los cuatro Cuadrantes.
- Explicar la diferencia entre coordinado polar y rectangular.
- Identificar los ejes programables en un mecanizado CNC.
EL SISTEMA DE COORDENADAS CARTESIANAS
Las coordenadas cartesianas permiten especificar la ubicación de un punto en el plano, o en el espacio tridimensional. Las coordenadas cartesianas o el sistema de coordenadas rectangulares de un punto son un par de números (en dos dimensiones) o un triplete de números (en tres dimensiones) que especifican distancias firmadas desde el eje de coordenadas. Primero debemos entender un sistema de coordenadas para definir nuestras direcciones y posición relativa. Sistema utilizado para definir puntos en el espacio mediante el establecimiento de direcciones (eje) y una posición de referencia (origen). Un sistema de coordenadas puede ser rectangular o polar.
Así como los puntos en la línea se pueden colocar en correspondencia uno a uno con la línea numérica real, así los puntos en plano se pueden colocar en correspondencia uno a uno con pares de líneas numéricas reales mediante el uso de dos líneas de coordenadas. Para ello, construimos dos líneas de coordenadas perpendiculares que se cruzan en sus orígenes; por conveniencia. Asignar un conjunto de graduaciones por igual espacio a los ejes x e y comenzando en el origen y yendo en ambas direcciones, se puede establecer el punto izquierdo y derecho (eje x) y arriba y abajo (eje y) a lo largo de cada eje. Hacemos vertical una de las líneas numéricas con su dirección positiva hacia arriba y dirección negativa hacia abajo. Las otras líneas numéricas horizontales con su dirección positiva a la derecha y dirección negativa a la izquierda. Las dos líneas numéricas se denominan ejes de coordenadas; la línea horizontal es el eje x, la línea vertical es el eje y, y los ejes de coordenadas juntos forman el sistema de coordenadas cartesianas o un sistema de coordenadas rectangular. El punto de intersección de los ejes de coordenadas se denota con O y es el origen del sistema de coordenadas. Ver Figura 1.
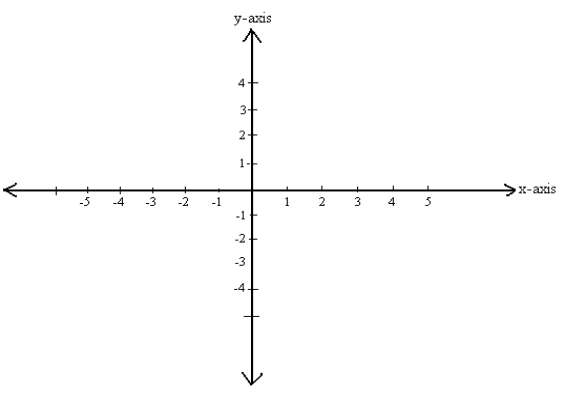
Figura 1
Básicamente es, Dos líneas de números reales juntas, una va de izquierda a derecha, y la otra va arriba-abajo. La línea horizontal se llama eje x y la línea vertical se llama eje y.
El Origen
Al punto (0,0) se le da el nombre especial “El Origen”, y a veces se le da la letra “O”.
Línea de número real
La base de este sistema es la línea numérica real marcada a intervalos iguales. El eje está etiquetado (X, Y o Z). Un punto de la línea se designa como el Origen. Los números de un lado de la línea están marcados como positivos y los del otro lado marcados como negativos. Ver Figura 2.
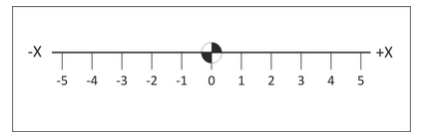
Figura 2. Línea numérica del eje X
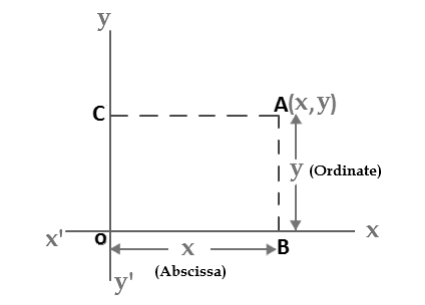
Coordenadas cartesianas del avión
Un plano en el que se ha introducido un sistema de coordenadas rectangular es un plano de coordenadas o un plano x-y. Ahora vamos a mostrar cómo establecer una correspondencia uno a uno entre puntos en un plano de coordenadas y pares de número real. Si A es un punto en un plano de coordenadas, entonces dibujamos dos líneas a través de A, una perpendicular al eje x y otra perpendicular al eje y. Si la primera línea cruza el eje x en el punto con la coordenada x y la segunda línea cruza el eje y en el punto con la coordenada y, entonces asociamos el par (x, y) con la A (Ver Figura 2). El número a es la coordenada x o abscisa de P y el número b es la coordenada y u ordenada de p; decimos que A es el punto con coordenada (x, y) y denotamos el punto por A (x, y). Al punto (0,0) se le da el nombre especial “El Origen”, y a veces se le da la letra “O”.
Abscisas y Ordenadas:
Las palabras “Abscisa” y “Ordenada”... son solo los valores x e y:
- Abscisa: el valor horizontal (“x”) en un par de coordenadas: qué tan lejos está el punto.
- Ordenada: el valor vertical (“y”) en un par de coordenadas: qué tan arriba o abajo está el punto.
