2.3: Forma polar vs. rectangular

Última actualización
Guardar como PDF

Page ID: 151466

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Forma polar

Al tratar con vectores, hay dos formas de expresarlos. Hasta este punto, hemos utilizado una magnitud y una dirección como 30 V @ 67°. Esto es lo que se conoce como la forma polar. Es más a menudo la forma en la que nos gusta expresar vectores.

Forma rectangular

La forma rectangular divide un vector en las coordenadas X e Y. En el siguiente ejemplo, tenemos un vector que, cuando se expresa como polar, es de 50 V @ 55 grados. El primer paso para encontrar esta expresión es usar los 50 V como hipotenusa y la dirección como ángulo. A continuación, trazamos una línea recta hacia abajo desde la punta de flecha hasta el eje X. ¿Qué aspecto te parece esto? Si dijiste triángulo rectángulo, date una palmadita en la espalda. Entonces podemos usar el ángulo y la hipotenusa para determinar el eje X con estas ecuaciones:

cos 55°×50 = 28.7 para el eje X
sin 55°×50 = 41 para el eje Y

Esto se logra con solo transponer las proporciones de lo que aprendimos previamente en trigonometría.

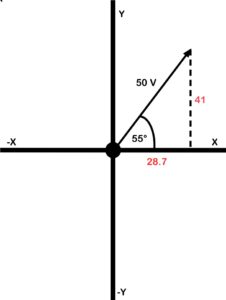
Figura 31. Cuadrante 1

Entonces podemos expresar el mismo vector que 28.7, j 41.

¿De dónde salió esa j?

La letra j se pone delante del componente y para indicar la diferencia entre la X y la Y. La razón j es esta.

Como forma de decir la diferencia entre X e Y, se decidió que se pusiera una letra frente a la Y. Los componentes X e Y realmente no existen, y son referidos como números imaginarios. Porque cada uno es un número imaginario, se sugirió la letra i. No obstante, la letra i también se usa como símbolo para corriente, por lo que se decidió ir con la letra j en su lugar.

Por qué la polaridad es importante

Veamos otro ejemplo. La forma polar es de 60 V @ 140 grados. Esto pone al vector en el segundo cuadrante.

En el segundo cuadrante, X es — (negativo) e Y es + (positivo). El ángulo de 140° se utiliza desde el punto 0°. Para utilizar la trigonometría, necesitamos determinar cuál es el ángulo en referencia al eje X. En este ejemplo, es 40° (el suplemento de 140°). Después de eso, podemos usar trigonometría para determinar los componentes X e Y.

cos 40°×60 = 46 para el eje X
sin 40°×60 = 39 para el eje Y

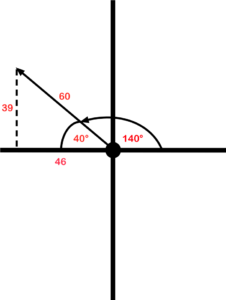
Figura 32. Cuadrante 2

Si vamos a expresarlo en forma rectangular, use -46, j39. Recuerde que el componente X es negativo y el componente Y es positivo ya que están en el segundo cuadrante.

¡Video! Este video explica cómo convertir de forma polar a forma rectangular.