8.3: El Amplificador “Operativo”
- Page ID
- 153778
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Mucho antes del advenimiento de la tecnología electrónica digital, se construyeron computadoras para realizar cálculos electrónicamente empleando voltajes y corrientes para representar cantidades numéricas. Esto fue especialmente útil para la simulación de procesos físicos. Un voltaje variable, por ejemplo, podría representar la velocidad o la fuerza en un sistema físico. Mediante el uso de divisores de voltaje resistivos y amplificadores de voltaje, las operaciones matemáticas de división y multiplicación podrían realizarse fácilmente en estas señales.
Las propiedades reactivas de capacitores e inductores se prestan bien a la simulación de variables relacionadas por funciones de cálculo. ¿Recuerdas cómo la corriente a través de un condensador era una función de la tasa de cambio del voltaje, y cómo esa tasa de cambio se designó en cálculo como la derivada? Bueno, si el voltaje a través de un condensador se hiciera para representar la velocidad de un objeto, la corriente a través del condensador representaría la fuerza requerida para acelerar o desacelerar ese objeto, representando la capacitancia del condensador la masa del objeto:
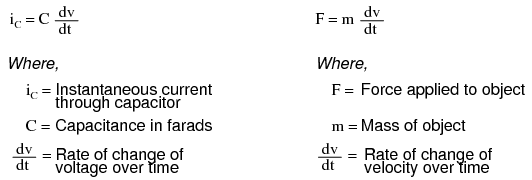
Este cálculo electrónico analógico de la función derivada de cálculo se conoce técnicamente como diferenciación, y es una función natural de la corriente de un condensador en relación con el voltaje aplicado a través de él. Tenga en cuenta que este circuito no requiere “programación” para realizar esta función matemática relativamente avanzada como lo haría una computadora digital.
Los circuitos electrónicos son muy fáciles y económicos de crear en comparación con los sistemas físicos complejos, por lo que este tipo de simulación electrónica analógica fue ampliamente utilizada en la investigación y desarrollo de sistemas mecánicos. Sin embargo, para una simulación realista, se necesitaban circuitos amplificadores de alta precisión y fácil configurabilidad en estas primeras computadoras.
Se encontró en el curso del diseño de computadoras analógicas que los amplificadores diferenciales con ganancias de voltaje extremadamente altas cumplieron con estos requisitos de precisión y configurabilidad mejor que los amplificadores de un solo extremo con ganancias diseñadas a medida. Utilizando componentes simples conectados a las entradas y salida del amplificador diferencial de alta ganancia, se podría obtener prácticamente cualquier ganancia y cualquier función del circuito, en general, sin ajustar o modificar la circuitería interna del propio amplificador. Estos amplificadores diferenciales de alta ganancia llegaron a ser conocidos como amplificadores operacionales, o amplificadores operacionales, debido a su aplicación en las operaciones matemáticas de computadoras analógicas.
Los amplificadores operacionales modernos, como el popular modelo 741, son circuitos integrados económicos y de alto rendimiento. Sus impedancias de entrada son bastante altas, las entradas dibujan corrientes en el rango de medio microamplificador (máximo) para el 741, y mucho menos para amplificadores operacionales que utilizan transistores de entrada de efecto de campo. La impedancia de salida suele ser bastante baja, aproximadamente 75 Ω para el modelo 741, y muchos modelos tienen protección de cortocircuito de salida incorporada, lo que significa que sus salidas pueden cortocircuitarse directamente a tierra sin causar daño a los circuitos internos. Con el acoplamiento directo entre las etapas de transistores internos de los amplificadores operacionales, pueden amplificar las señales de CC tan bien como la CA (hasta ciertos límites máximos de voltaje-tiempo de subida). Costaría mucho más en dinero y tiempo diseñar un circuito amplificador de transistor discreto comparable para que coincida con ese tipo de rendimiento, a menos que se requiera una alta capacidad de potencia. Por estas razones, los amplificadores operacionales tienen todos menos amplificadores de señal de transistor discreto obsoleto en muchas aplicaciones.
El siguiente diagrama muestra las conexiones de clavija para amplificadores operacionales individuales (741 incluidos) cuando están alojados en un circuito integrado DIP (D ual I nline P ackage) de 8 pines:
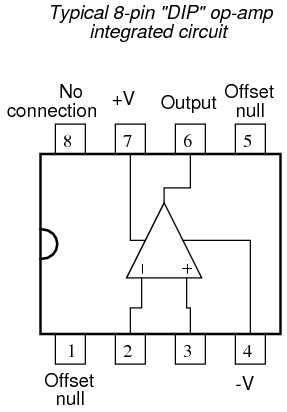
Algunos modelos de op-amp vienen dos a un paquete, incluidos los populares modelos TL082 y 1458. Estas se llaman unidades “duales”, y normalmente se alojan en un paquete DIP de 8 pines también, con las siguientes conexiones de pines:
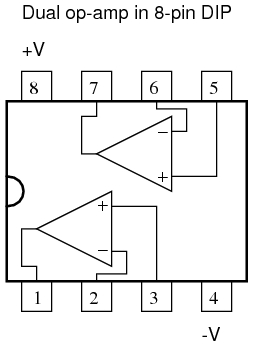
Los amplificadores operacionales también están disponibles de cuatro a un paquete, generalmente en arreglos DIP de 14 pines. Desafortunadamente, las asignaciones de pines no son tan estándar para estos amplificadores operacionales “cuádruples” como para las unidades “duales” o individuales. Consulte las hojas de datos del fabricante para obtener más detalles.
Las ganancias prácticas de voltaje del amplificador operacional están en el rango de 200,000 o más, lo que los hace casi inútiles como amplificador diferencial analógico por sí mismos. Para un amplificador operacional con una ganancia de voltaje (A V) de 200,000 y una oscilación de voltaje de salida máxima de +15V/-15V, ¡todo lo que se necesitaría es un voltaje de entrada diferencial de 75 µV (microvoltios) para llevarlo a saturación o corte! Antes de echar un vistazo a cómo se utilizan los componentes externos para reducir la ganancia a un nivel razonable, investiguemos las aplicaciones para el amplificador operacional “desnudo” por sí mismo.
Una aplicación se llama comparador. Para todos los propósitos prácticos, podemos decir que la salida de un op-amp se saturará completamente positiva si la entrada (+) es más positiva que la entrada (-), y saturada completamente negativa si la entrada (+) es menos positiva que la entrada (-). En otras palabras, la ganancia de voltaje extremadamente alta de un amplificador operacional lo hace útil como dispositivo para comparar dos voltajes y cambiar los estados de voltaje de salida cuando una entrada excede a la otra en magnitud.
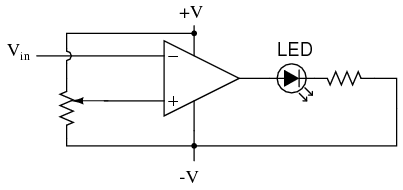
En el circuito anterior, tenemos un amplificador operacional conectado como comparador, comparando el voltaje de entrada con un voltaje de referencia establecido por el potenciómetro (R 1). Si V in cae por debajo del voltaje establecido por R1, la salida del amplificador operacional se saturará a +V, iluminando así el LED. De lo contrario, si V in está por encima del voltaje de referencia, el LED permanecerá apagado. Si V in es una señal de voltaje producida por un instrumento de medición, este circuito comparador podría funcionar como una alarma “baja”, con el punto de disparo establecido por R1. En lugar de un LED, la salida de amplificador operacional podría accionar un relé, un transistor, un SCR o cualquier otro dispositivo capaz de conmutar la energía a una carga, como una válvula de solenoide, para tomar medidas en caso de una alarma baja.
Otra aplicación para el circuito comparador mostrado es un convertidor de onda cuadrada. Supongamos que el voltaje de entrada aplicado a la entrada inversora (-) era una onda sinusoidal de CA en lugar de una tensión de CC estable. En ese caso, el voltaje de salida pasaría entre estados opuestos de saturación siempre que el voltaje de entrada fuera igual al voltaje de referencia producido por el potenciómetro. El resultado sería una onda cuadrada:
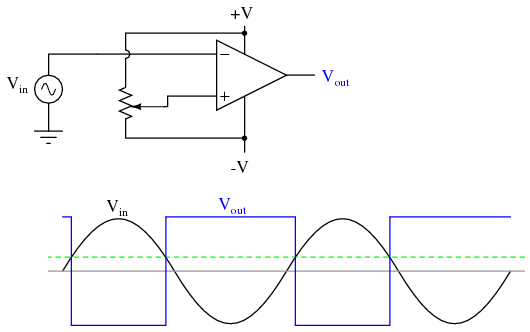
Los ajustes a la configuración del potenciómetro cambiarían el voltaje de referencia aplicado a la entrada no inversora (+), lo que cambiaría los puntos en los que cruzaría la onda sinusoidal, cambiando los tiempos de encendido/apagado o el ciclo de trabajo de la onda cuadrada:
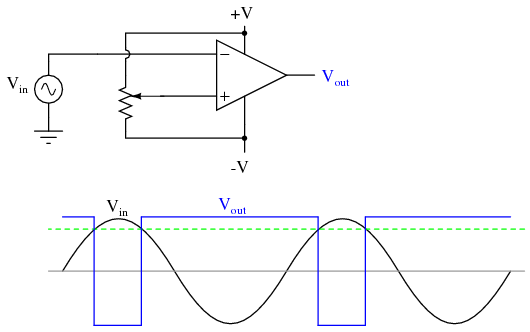
Debe ser evidente que el voltaje de entrada de CA no tendría que ser una onda sinusoidal en particular para que este circuito realice la misma función. El voltaje de entrada podría ser una onda triangular, onda en diente de sierra o cualquier otro tipo de onda que volviera a aumentar suavemente de positiva a negativa a positiva. Este tipo de circuito comparador es muy útil para crear ondas cuadradas de ciclo de trabajo variable. Esta técnica a veces se denomina modulación por ancho de pulso, o PWM (variando, o modulando una forma de onda de acuerdo con una señal de control, en este caso la señal producida por el potenciómetro).
Otra aplicación comparadora es la del controlador de bargraph. Si tuviéramos varios amplificadores operacionales conectados como comparadores, cada uno con su propio voltaje de referencia conectado a la entrada inversora, pero cada uno monitoreando la misma señal de voltaje en sus entradas no inversoras, podríamos construir un medidor estilo barógrafo como lo que comúnmente se ve en la cara de sintonizadores estéreo y gráficos ecualizadores. A medida que aumentaba el voltaje de la señal (que representa la intensidad de la señal de radio o el nivel de sonido de audio), cada comparador se “encendería” en secuencia y enviaría energía a su respectivo LED. Con cada comparador encendiendo “” a un nivel diferente de sonido de audio, el número de LED iluminados indicaría qué tan fuerte era la señal.
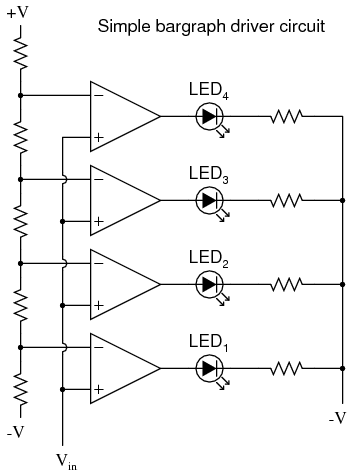
En el circuito que se muestra arriba, el LED 1 sería el primero en encenderse a medida que el voltaje de entrada aumentaba en una dirección positiva. A medida que el voltaje de entrada continuaba aumentando, los otros LED se iluminarían sucesivamente, hasta que todos estuvieran encendidos.
Esta misma tecnología se utiliza en algunos convertidores de señal analógico-digital, a saber, el convertidor flash, para traducir una cantidad de señal analógica en una serie de voltajes de encendido/apagado que representan un número digital.
Revisar
- Una forma de triángulo es el símbolo genérico de un circuito amplificador, el extremo ancho significa la entrada y el extremo estrecho significa la salida.
- A menos que se especifique lo contrario, todos los voltajes en los circuitos amplificadores se refieren a un punto de tierra común, generalmente conectado a un terminal de la fuente de alimentación. De esta manera, podemos hablar de cierta cantidad de voltaje estando “en” un solo cable, al tiempo que nos damos cuenta de que el voltaje siempre se mide entre dos puntos.
- Un amplificador diferencial es uno que amplifica la diferencia de voltaje entre dos entradas de señal. En dicho circuito, una entrada tiende a conducir el voltaje de salida a la misma polaridad de la señal de entrada, mientras que la otra entrada hace justo lo contrario. En consecuencia, la primera entrada se denomina entrada no inversora (+) y la segunda se denomina entrada inversora (-).
- Un amplificador operacional (o amplificador operacional para abreviar) es un amplificador diferencial con una ganancia de voltaje extremadamente alta (A V = 200,000 o más). Su nombre proviene de su uso original en circuitos informáticos analógicos (realizando operaciones matemáticas).
- Los amplificadores operacionales suelen tener impedancias de entrada muy altas e impedancias de salida bastante bajas.
- A veces, los amplificadores operacionales se utilizan como comparadores de señal, operando en modo de corte completo o saturación dependiendo de qué entrada (inversora o no inversora) tenga el mayor voltaje. Los comparadores son útiles para detectar condiciones de señal “mayores que” (comparando una con la otra).
- Una aplicación de comparador se llama modulador de ancho de pulso, y se realiza comparando una señal de CA de onda sinusoidal con una tensión de referencia de CC. A medida que se ajusta el voltaje de referencia de CC, la salida de onda cuadrada del comparador cambia su ciclo de trabajo (tiempos positivos frente a negativos). Por lo tanto, el voltaje de referencia de CC controla o modula el ancho de pulso de la tensión de salida.


