1.7: Estructuras

Volvamos, a modo de ejemplo, al lenguaje\(\mathcal{L}_{NT}\) de la teoría de números. Recordemos\(\mathcal{L}_{NT}\) es decir\(\{ 0, S, +, \cdot, E, <\}\), donde 0 es un símbolo constante,\(S\) es un símbolo de función unario,\(+\)\(\cdot\), y\(E\) son símbolos de función binarios, y\(<\) es un símbolo de relación binaria. Ahora queremos discutir las posibles estructuras matemáticas en las que podemos interpretar estos símbolos, y así las fórmulas y frases de\(\mathcal{L}_{NT}\).

“¡Pero espera!” llora el lector incrédulo. “Acabas de decir que este es el lenguaje de la teoría de números, así que desde luego ya sabemos lo que significa cada uno de esos símbolos”.

Sin duda es el caso de que conoces una interpretación para estos símbolos. El punto de esta sección es que existen muchas interpretaciones posibles diferentes para estos símbolos, y queremos poder precisar cuál de esas interpretaciones tenemos en mente en un momento determinado.

Probablemente la interpretación que tenías en mente (lo que llamaremos el modelo estándar para la teoría de números) funciona con el conjunto de números naturales\(\{ 0, 1, 2, 3, \ldots \}\). El símbolo 0 representa el número 0.

Chaff: ¡Con cuidado, ahora! El símbolo 0 es la marca en el papel, el numeral. El número 0 es lo que representa el numeral 0. El numeral es algo que se puede ver. El número es algo que no se puede ver.

El símbolo\(S\) es un símbolo de función unaria, y la función para la que se encuentra ese símbolo es la función sucesora que asigna un número al siguiente número natural mayor. Los símbolos\(+\)\(\cdot\), y\(E\) representan las funciones de suma, multiplicación y exponenciación, y el símbolo se\(<\) utilizará para la relación “menor que”.

Pero esa es sólo una de las formas que podríamos elegir para interpretar esos símbolos. Otra forma de interpretar todos esos símbolos sería trabajar con los números 0 y 1, interpretando el símbolo 0 como el número 0,\(S\) como la función que mapea 0 y 1 y 1 a 0,\(+\) como adición mod 2,\(\cdot\) como multiplicación mod 2, y (solo por variedad)\(E\) como la función con valor constante 1. El símbolo aún\(<\) puede representar la relación “menos que”.

O, si estuviéramos en un estado de ánimo un poco más extraño, podríamos trabajar en un universo formado por Beethoven, Picasso y Ernie Banks, interpretando el símbolo 0 como Picasso,\(S\) como la función de identidad,\(<\) como igualdad, y cada uno de los símbolos de función binaria como la función constante con salida Ernie Bancos.

El punto es que no hay nada sagrado en una estructura matemática en contraposición a otra. Sin determinar la estructura en cuestión, sin decidir cómo queremos interpretar los símbolos de la lengua, no tenemos forma de hablar de la verdad o falsedad de una oración tan trivial como

\[\left( \forall v_1 \right) \left( v_1 < S \left( v_1 \right) \right).\]

Definición 1.6.1. Arreglar un idioma\(\mathcal{L}\). Una \(\mathcal{L}\)-estructura\(\mathfrak{A}\) es un conjunto no vacío\(A\), llamado universo de\(\mathfrak{A}\), junto con:

1. Para cada símbolo constante\(c\) de\(\mathcal{L}\), un elemento\(c^\mathfrak{A}\) de\(A\),
2. Para cada símbolo de función\(n\) -aria\(f\) de\(\mathcal{L}\), una función\(f^\mathfrak{A} : A^n \rightarrow A\), y
3. Para cada símbolo\(R\) de relación\(n\) -aria de\(\mathcal{L}\), una relación\(n\) -aria\(R^\mathfrak{A}\) en\(A\) (es decir, un subconjunto de\(A^n\)).

Observe que el dominio de la función\(f^\mathfrak{A}\) es el conjunto\(A^n\), por lo que\(f^\mathfrak{A}\) se define para todos los elementos de\(A^n\). Más adelante en el texto tendremos ocasión de discutir funciones parciales, aquellas cuyo dominio en un subconjunto propio de\(A^n\), pero por ahora nuestras funciones son funciones totales, definidas en todo el dominio anunciado.

Chaff: La carta\(\mathfrak{A}\) es una Frakture alemana mayúscula A. También tendremos ocasión de usar a los amigos\(\mathfrak{A}\) de,\(\mathfrak{B}\) y\(\mathfrak{C}\). \(\mathfrak{N}\)se utilizará para una estructura particular que involucre los números naturales. El uso de este tipo de letra es tradicional (lo que significa que así es como lo aprendimos). Para tu trabajo escrito a mano, probablemente el uso de letras mayúsculas será lo mejor.

A menudo, escribiremos una estructura como una\(k\) tupla ordenada, así:

\[\mathfrak{A} = \left( A, c_1^\mathfrak{A}, c_2^\mathfrak{A}, f_1^\mathfrak{A}, R_1^\mathfrak{A}, R_2^\mathfrak{A} \right).\]

Como pueden ver, la notación está empezando a salirse de control una vez más, y no dudaremos en simplificar y abreviar cuando creemos que podemos hacerlo sin confusión. Entonces, cuando estamos trabajando en\(\mathcal{L}_{NT}\), a menudo hablaremos de la estructura estándar

\[\mathfrak{N} = \left( \mathbb{N}, 0, S, +, \cdot, E, < \right),\]

donde las constantes, funciones y relaciones no obtienen los superíndices que se merecen, y los autores confían en que interpretará\(\mathbb{N}\) como la colección\(\{0, 1, 2, \ldots \}\) de números naturales, el símbolo 0 para representar el número 0,\(+\) para representar la suma,\(S\) para representar al sucesor función, y así sucesivamente. Por cierto, si no estás acostumbrado a pensar en 0 como un número natural, no entres en pánico. Los teóricos del conjunto ven 0 como el más natural de los objetos, por lo que tendemos a incluirlo en\(\mathbb{N}\) sin pensarlo.

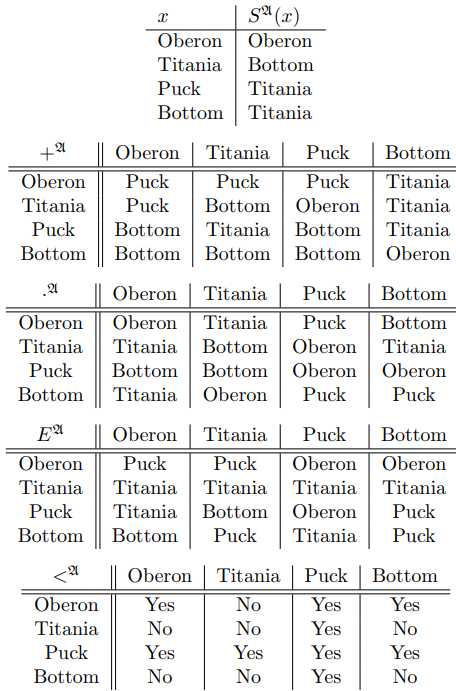
Cuadro 1.1: Estructura de una noche de solsticio de verano

Ejemplo 1.6.2. La estructura\(\mathfrak{N}\) que acabamos de introducir se llama la\(\mathcal{L}_{NT}\) estructura estándar. Para enfatizar que hay otras\(\mathcal{L}_{NT}\) estructuras perfectamente buenas, construyamos una\(\mathcal{L}_{NT}\) estructura diferente\(\mathfrak{A}\) con exactamente cuatro elementos. Los elementos de\(A\) serán Oberon, Titania, Puck y Bottom. La constante\(0^\mathfrak{A}\) será Bottom. Ahora tenemos que construir las funciones y relaciones para nuestra estructura. Como todo es unario o binario, establecer tablas (como en la Tabla 1.1) parece una manera razonable de proceder. Entonces se puede ver que en esta estructura\(\mathfrak{A}\) que Titania\(+\) Puck\(=\) Oberon, mientras que Puck\(+\) Titania\(=\) Titania. También se puede ver que 0 (también conocido como Bottom) no es la identidad aditiva en esta estructura, y ese\(<\) es un ordenamiento muy extraño.

Ahora bien, las funciones particulares y la relación que elegimos fueron solo las funciones y relaciones que saltaron a los dedos de Chris mientras escribía este ejemplo, pero cualquiera de esas funciones habría funcionado perfectamente bien para definir una\(\mathcal{L}_{NT}\) -estructura. Bien puede valer la pena averiguar si esta\(\mathcal{L}_{NT}\) frase es cierta (lo que sea que eso signifique) en\(\mathfrak{A}\):\(SS0 + SS0 < SSSSS0E0 + S0\).

Ejemplo 1.6.3. Trabajamos en un lenguaje con un símbolo constante,\(\mathfrak{L}\), y un símbolo de función unaria,\(X\). Entonces, para definir un modelo\(\mathfrak{A}\), todo lo que necesitamos hacer es especificar un universo, un elemento del universo, y una función\(X^\mathfrak{A}\). Supongamos que dejamos que el universo sea la colección de todas las cadenas finitas de 0 o más letras mayúsculas del alfabeto romano. Entonces\(A\) incluye cadenas tales como: BABY, LOGICISBETTERTHANSIX,\(\varepsilon\) (la cadena vacía), y DLKFDFAHADS. El símbolo constante se\(\mathfrak{L}\) interpretará como la cadena POTITION, y la función\(X^\mathfrak{A}\) es la función que agrega una X al comienzo de una cadena. Entonces\(X^\mathfrak{A}\) (\(=\)YLOPHONE) XILÓPHONE. Convénzase de que esta es una\(\mathcal{L}\) estructura válida, aunque algo extraña.

Para tratar de tener claro las cosas, fíjate que tenemos\(X\), el símbolo de función, que es un elemento del lenguaje\(\mathcal{L}\). Luego está X, la cadena de exactamente una letra mayúscula del alfabeto romano, que es uno de los elementos del universo. (¿Notaste el cambio de tipografía sin que nosotros lo señaláramos? ¡Puede que tengas futuro en la publicación!)

Veamos uno de los términos del lenguaje:\(X \mathfrak{L}\). En nuestra\(\mathcal{L}\) estructura particular\(\mathfrak{A}\) interpretaremos esto como

\[X^\mathfrak{A} \left( \mathfrak{L}^\mathfrak{A} \right) = X^\mathfrak{A} \left( \text{POTITION} \right) = \text{XPOTITION}.\]

En una estructura diferente,\(\mathfrak{B}\), es totalmente posible que la interpretación del término\(X \mathfrak{L}\) sea HUNNY o AARVARK o\(3 \pi / 17\). Sin conocer la estructura, sin saber interpretar los símbolos de la lengua, no podemos comenzar a saber a qué objeto se refiere un término.

Chaff: Todo esto sobre interpretar términos en una estructura se hará formal en la siguiente sección, así que no se asuste si no todo tiene sentido en este momento.

Lo que hace que este ejemplo sea confuso, además de importante, es que el símbolo de función es parte de la estructura para el lenguaje y (módulo a superíndice y un cambio de tipografía) la función actúa sobre los elementos de la estructura de la misma manera que se utiliza el símbolo de función en la creación de\(\mathcal{L}\) -fórmulas.

Ejemplo 1.6.4. Ahora,\(\mathcal{L}\) seamos\(\{0, f, g, R\}\), donde 0 es un símbolo constante,\(f\) es un símbolo de función unario,\(g\) es un símbolo de función binaria, y\(R\) es un símbolo de relación 3-aria. Definimos una\(\mathcal{L}\) estructura de la\(\mathfrak{B}\) siguiente manera:\(B\), el universo, es el conjunto de todos los\(\mathcal{L}\) términos libres de variables. La constante\(0^\mathfrak{B}\) es el término 0. Las funciones\(f^\mathfrak{B}\) y\(g^\mathfrak{B}\) se definen como en el Ejemplo 1.6.3, así que si\(t\) y\(s\) son elementos de\(B\), (es decir, términos libres de variables), entonces\(f^\mathfrak{B} \left( t \right)\) es\(ft\) y\(g^\mathfrak{B} \left( t, s \right)\) es\(gts\).

Veamos esto con un poco más de detalle. Considera 0, el símbolo constante, que es un elemento de\(\mathcal{L}\). Ya que 0 es un símbolo constante, es un término, entonces 0 es un elemento de\(B\), el universo de nuestra estructura\(\mathfrak{B}\). (Ay, no hay ningún cambio en la tipografía que nos ayude esta vez.) Si queremos ver a qué elemento del universo se refiere el símbolo constante 0, vemos eso\(0^\mathfrak{B} = 0\), por lo que el término 0 se refiere al elemento del universo 0.

Si miramos otro término del lenguaje, digamos\(f0\), e intentamos encontrar el elemento del universo que se denota con este término, encontramos que es

\[f^\mathfrak{B} \left( 0^\mathfrak{B} \right) = f^\mathfrak{B} \left( 0 \right) = f0.\]

Entonces el término\(f0\) denota un elemento del universo, y ese elemento del universo es... \(f0\). Esto es bastante confuso, pero todo lo que está pasando es que los elementos del universo son los objetos sintácticos del lenguaje.

Este tipo de estructura se llama estructura Henkin, después de Leon Henkin, quien las introdujo en su tesis doctoral en 1949. Estas estructuras serán cruciales en nuestra prueba del Teorema de la Integtud en el Capítulo 3. La prueba de ese teorema implicará la construcción de una estructura matemática particular, y la estructura que construiremos será una estructura Henkin.

Para terminar de construir nuestra estructura\(\mathfrak{B}\), tenemos que definir una relación\(R^\mathfrak{B}\). Como\(R\) es un símbolo de relación 3-aria,\(R^\mathfrak{B}\) es un subconjunto de\(B^3\). Vamos a definir arbitrariamente

\[R^\mathfrak{B} = \{ \left( r, s, t \right) \in B^3 \: | \: \text{the number of function symbols in } r \: \text{is even} \}.\]

Esto termina definiendo la estructura\(\mathfrak{B}\). La definición de\(R^\mathfrak{B}\) dado es totalmente arbitraria. Te invitamos a llegar a una definición más interesante o más humorística por tu cuenta.

Ejercicios

1. Consideremos la estructura construida en el Ejemplo 1.6.2. Encuentra el valor de cada uno de los siguientes:\(0 + 0\),\(0E0\),\(S0 \cdot SS0\). ¿Crees que\(0 < 0\) es cierto en esta estructura?
2. Supongamos que ese\(\mathcal{L}\) es el idioma\(\{0, +, <\}\). Trabajemos juntos para describir una\(\mathcal{L}\) -estructura\(\mathfrak{A}\). Que el universo\(A\) sea el conjunto formado por todos los números naturales junto con Ingrid Bergman y Humphrey Bogart. Tú decides sobre las interpretaciones de los símbolos. ¿Cuál es el valor de\(5 +\) Ingrid? ¿Es Bogie\(< 0\)?
3. Aquí hay un lenguaje que consiste en un símbolo constante, un símbolo de función 3-aria, y un símbolo de relación binaria:\(\mathcal{L}\) es\(\{\flat, \sharp, \natural\}\). Describir un\(\mathcal{L}\) -modelo que tiene como universo\(\mathbb{R}\), el conjunto de números reales. Describir otro\(\mathcal{L}\) -modelo que tiene un universo finito.
4. Escribe un breve párrafo explicando la diferencia entre un idioma y una estructura para un idioma.
5. Supongamos que\(\mathfrak{A}\) y\(\mathfrak{B}\) son dos\(\mathcal{L}\) -estructuras. Diremos eso\(\mathfrak{A}\) y\(\mathfrak{B}\) son isomórficos y escribimos\(\mathfrak{A} \cong \mathfrak{B}\) si hay una biyección\(i : A \rightarrow B\) tal que por cada símbolo constante\(c\) de\(\mathcal{L}\),\(i \left( c^\mathfrak{A} \right) = c^\mathfrak{B}\), para cada símbolo\(n\) -ario de función\(f\) y para cada uno\(a_1, \ldots, a_n \in A\),\(i \left( f^\mathfrak{A} \left( a_1, \ldots, a_n \right) \right) = f^\mathfrak{B} \left( i \left( a_1 \right), \ldots i \left( a_n \right) \right)\), y para cada símbolo de relación\(n\) -aria\(R\) en\(\mathcal{L}\),\(\left( a_1, \ldots a_n \right) \in R^\mathfrak{A}\) si y sólo si\(\left( i \left( a_1 \right), \ldots, i \left( a_n \right) \right) \in R^\mathfrak{B}\). La función\(i\) se llama isomorfismo.
   (a) Demostrar que\(\cong\) es una relación de equivalencia. [Sugerencia: Esto significa que se debe demostrar que la relación\(\cong\) es reflexiva, simétrica y transitiva. Para demostrar que\(\cong\) es reflexivo, debes demostrar eso para cualquier estructura\(\mathfrak{A}\)\(\mathfrak{A} \cong \mathfrak{A}\), lo que significa que debes encontrar un isomorfismo, una función, mapeado\(A\) a\(A\) que satisfaga las condiciones anteriores. Entonces la primera línea de tu prueba debería ser, “Considera esta función, con dominio\(A\) y codominio\(A : i \left( x \right) =\) [algo brillante]”. Entonces demuestre que su función\(i\) es un isomorfismo. Entonces muestra, si\(\mathfrak{A} \cong \mathfrak{B}\), entonces\(\mathfrak{B} \cong \mathfrak{A}\). Después, abordar la transitividad. En cada caso, debes definir una función en particular y demostrar que tu función es un isomorfismo.]
   (b) Encontrar una nueva estructura que sea isomórfica a la estructura dada en el Ejemplo 1.6.2. Demostrar que las estructuras son isomórficas.
   (c) Encontrar dos estructuras diferentes para un lenguaje en particular y demostrar que no son isomórficas.
   (d) Encontrar dos estructuras diferentes para un lenguaje particular de tal manera que las estructuras tengan el mismo número de elementos en sus universos pero aún no sean isomorficas.Demostrar que no son isomórficas.
6. Toma el lenguaje del Ejemplo 1.6.4 y deja\(C\) ser el conjunto de todos los\(\mathcal{L}\) -términos. Crear una\(\mathcal{L}\) -estructura\(\mathfrak{C}\) utilizando este universo de tal manera que la interpretación de un término no\(t\) sea igual a\(t\).
7. Si tomamos el lenguaje\(\mathcal{L}_{NT}\), podemos crear una estructura Henkin para ese idioma de la misma manera que en el Ejemplo 1.6.4. Hazlo. Considera la\(\mathcal{L}_{NT}\) fórmula\(S0 + S0 = SS0\) -. ¿Esta fórmula es “verdadera” (lo que sea que eso signifique) en tu estructura? Justifica tu respuesta.