17.7: Comparando diferentes métodos
- Page ID
- 54142
La principal diferencia entre Gibbs, EM y el algoritmo Greedy radica en su paso de maximización después de calcular su matriz Z. Ejemplos de la matriz Z se representan gráficamente a continuación.Esta matriz Z se utiliza entonces para volver a calcular la matriz de perfil original hasta la convergencia. Algunos ejemplos de esta matriz están representados gráficamente por 17.8
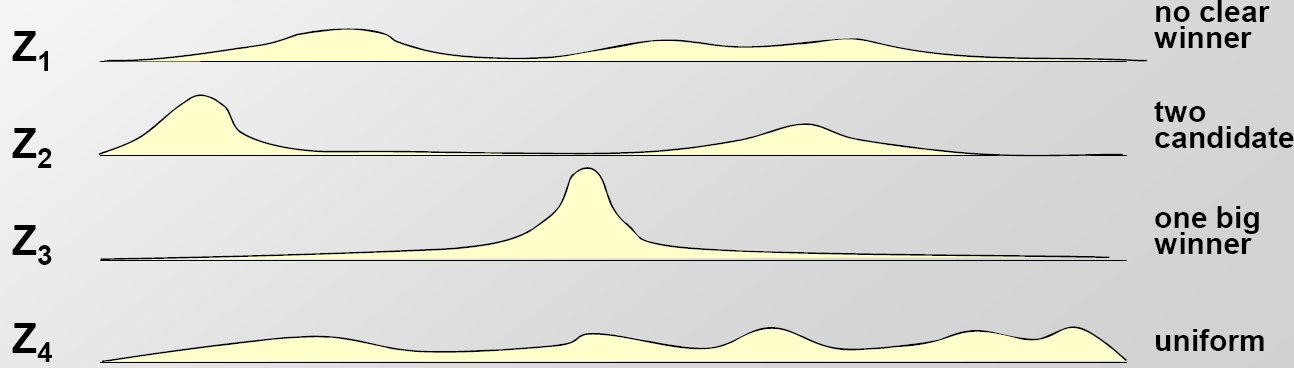
Figura 17.8: Ejemplos de la matriz Z calculada a través de EM, muestreo de Gibbs y el algoritmo codicioso
Intuitivamente, el algoritmo codicioso siempre escogerá la ubicación más probable para el motivo. El algoritmo EM tomará un promedio de todos los valores, mientras que Gibbs Sampling utilizará realmente la distribución de probabilidad dada por Z para muestrear un motivo en un paso.

Figura 17.9: Selección de la ubicación del motivo: el algoritmo codicioso siempre escogerá la ubicación más probable para el motivo. El algoritmo EM tomará un promedio mientras que Gibbs Sampling utilizará realmente la distribución de probabilidad dada por Z para muestrear un motivo en cada paso


