4.3: Derivar relaciones energéticas simples
- Page ID
- 53810
A. Energía en el Universo: el Universo es un Sistema Cerrado
Considera un evento, cualquiera incluso. Creo que podemos estar de acuerdo en que cuando pasan cosas, los participantes en el suceso pasan de un estado inestable a un estado relativamente más estable. Por ejemplo, llevas una bolsa de canicas y accidentalmente la dejas caer. Las canicas caerían al suelo, rodarían y se extendían, llegando finalmente a un alto. En ese punto, las canicas están en un estado más estable que cuando estabas sujetando la bolsa.
Si se le pregunta, dirías que la gravedad hizo que las canicas cayeran de la bolsa. Eso es ciertamente cierto. ¿Podríamos decir entonces que el impulso a una mayor estabilidad es lo que hizo caer las canicas? De hecho, independientemente de la fuerza o ímpetu para el evento, podemos decir que el impulso para lograr una mayor estabilidad que haga que las cosas/eventos sucedan! Esta es la esencia de la Segunda Ley de la Termodinámica: todos los eventos universales de transferencia de energía ocurren con un incremento en la estabilidad..., es decir, un incremento de la entropía. En breve consideraremos la segunda ley y la entropía en detalle.
La tendencia de que las cosas pasen de inestables a más estables es un estado de cosas natural, racional..., como esas canicas en el piso, o una recámara desordenada con ropa esparcida por ahí. Intuitivamente, desordenado y desordenado es más estable que ordenado. Por supuesto, las canicas que caen o la ropa que va de plegada y colgada a arrugada en el piso libera energía (energía potencial) a medida que caen (energía cinética). Si no crees que esta liberación de energía sea real, solo piensa en cuánta energía necesitarás para recoger las canicas o volver a doblar tu ropa (¡después de lavarlas por supuesto!).
Podemos modelar el flujo de energía en el universo de una manera que sea consistente con las leyes termodinámicas. Dado que la Primera Ley de la Termodinámica dice que la energía no puede crearse ni destruirse, una simple declaración de la Primera Ley podría ser:
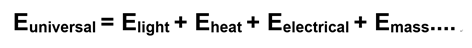
La ecuación resume los diferentes tipos de energía en el universo. Míralo de esta manera:
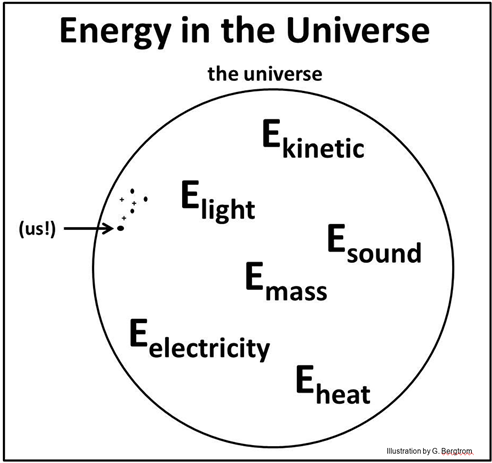
La energía no puede entrar ni salir del universo. La energía sólo puede transferirse de un lugar a otro, o convertirse de una forma a otra. Se deduce entonces que E universal es la suma de todo tipo de energía en el universo, y que esta suma es una constante. La siguiente ecuación es consistente con esta idea.
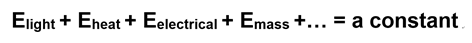
Se trata de una declaración de la Primera Ley de la Termodinámica.
139 Primera Ley de Termodinámica
Si vamos con la noción binaria más simple o energía útil e inútil, nuestra ecuación se acorta a la suma de solo dos tipos de energía en el universo:
En esta ecuación, G es energía útil (energía libre “Gibbs”), S es energía inútil (entropía) y T es temperatura absoluta (incluida por la tercera ley). Esto también es una declaración de la Primera Ley. Aquí está nuestro diagrama circular revisado:
Por cierto, segregar cosas y conceptos en círculos es una forma de ver lógicamente las relaciones entre ellos. John Venn formalizó por primera vez este enfoque a finales del siglo XIX. Los diagramas de Venn utilizados aquí para describir el universo son muy simples. Para ejemplos de componentes superpuestos más complejos del universo que comparten algunos pero no todos los atributos, “Google” Venn Diagramas.
En este modelo energético binario, se deduce que a medida que aumenta la entropía universal, la energía libre en el universo debe disminuir:
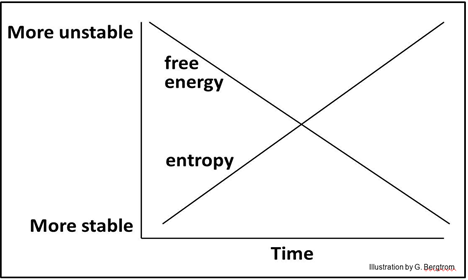
La energía libre o 'potencialmente útil' es mayor en sistemas más ordenados, complejos y por lo tanto relativamente inestables. Tales sistemas inestables y ordenados liberarán energía libre de manera espontánea.
140 Termodinámica de Segunda Ley
Si bien las declaraciones aritméticas sobre los cambios en la energía son conceptos útiles, los parámetros son por supuesto, ¡no medibles! Pero si aislamos un poco del universo, podemos medir energías y observar el flujo de energía.
B. La energía se intercambia entre sistemas en el universo
Si podemos medir la cantidad de energía puesta o eliminada de un sistema dentro del universo, podemos escribir una ecuación más útil para seguir la transferencia de energía entre un sistema y su entorno:
\[ΔH = ΔG + TΔS\]
En esta fórmula,\(ΔH\) se encuentra el cambio (D) en la entalpía, es decir, como energía que entra/sale del sistema en unidades de energía térmica);\(ΔG\) es cambio en energía libre y\(ΔS\) es cambio en entropía; T = temperatura absoluta (OK).
El calor emitido en una reacción (u otro evento) a menudo se confunde con la entropía. Es cierto que gran parte del aumento de la entropía que se produce en los seres vivos es efectivamente en forma de movimiento molecular aleatorio, o calor. Pero recuerda que el calor puede tener sus usos; ¡no todo el calor es entrópico! De ahí que sea más interesante (¡y preciso!) pensar en la energía en términos de cambios en entalpía, energía libre y entropía durante las transferencias de energía.
Según la ecuación\(ΔH = ΔG + TΔS\), los sistemas que interactúan en nuestro universo parecerían ser sistemas cerrados. En consecuencia, la energía puesta o retirada del sistema (\(ΔH\)) se equilibrará exactamente por aumentos y/o disminuciones en los otros dos términos de la ecuación (\(ΔG + TΔS\)). Recordemos que nos referimos a estos sistemas como sistemas cerrados no porque estén realmente cerrados, sino porque podemos aislarlos lo suficientemente bien como para dar cuenta del flujo de energía que entra y sale del sistema. El valor de esta (o cualquier) ecuación algebraica con tres variables es que si conoces dos de los valores, ¡puedes calcular la tercera! Aquí una situación sencilla para ilustrar el punto: Si pongo un litro de agua en un quemador y enciendo la llama, el agua se calienta. Si la temperatura del litro de agua sube 1oC, sabemos que ha absorbido 1000 calorías (una Kcal, o una caloría alimenticia) del calor del quemador.
Dado que las interacciones energéticas dependen de diferentes condiciones físicas, como la temperatura y la presión del aire, necesitamos estandarizar esas condiciones al realizar experimentos que midan los cambios de energía en sistemas aislados experimentalmente. Para obtener más información sobre cómo estandarizar estos parámetros físicos permite medir el cambio de energía en las reacciones químicas (de hecho, cualquier intercambio de energía), haga clic en el siguiente enlace.
141 Derivando Termodinámica de Sistema Cerrado
Volviendo a la bioenergética, apliquemos la ecuación\(ΔH = ΔG + TΔS\) a las reacciones químicas en las células. Debido a que la mayor parte de la vida en la tierra vive al nivel del mar donde la presión del aire es de 1 atmósfera y la temperatura está en los años 20 (Celsius)\(ΔH\)\(ΔG\), determinaciones típicas de, y\(ΔS\) se realizan bajo condiciones estándar donde t=298OK (25oC), una atmosférica presión de presiones de 1 atm, y un pH constante de 7.0. Además, los valores medidos se ajustan para calcular cantidades unimolares de reactivos (ver abajo). Nuestra ecuación para las reacciones bajo estas condiciones estándar se convierte en:\(ΔH = ΔGo + TΔS\), donde\(ΔGo\) está el cambio de energía libre estándar para la reacción realizada en un sistema cerrado bajo condiciones estándar, mientras que\(ΔH\) y\(ΔS\) siguen siendo los cambios de entalpía y entropía, pero determinados bajo condiciones estándar.
¿Cuáles son las condiciones unimolares en la práctica? Significa que si quemas 180 mg de glucosa en un calorímetro, multiplica las calorías liberadas (\(ΔH\)) por 1000. Esto te da las calorías liberadas al quemar 180 gm (es decir, un mol entero) de las cosas. Ahora estamos listos para considerar ejemplos de cómo determinamos la energética de las reacciones.
c. ¿Cómo se determina el cambio de entalpía (\(ΔH\))?
\(ΔH\)para una reacción química se puede determinar fácilmente realizando la reacción en condiciones estándar en un calorímetro de bomba (ilustrado a continuación).
Los fabricantes de alimentos determinan el contenido calórico de los alimentos usando un calorímetro de bomba. Como ocurre una reacción en el vaso de precipitados de la ilustración, éste liberará o absorberá calor, ya sea calentando o enfriando el agua en la camisa del calorímetro, según lo medido por el termómetro. Una reacción que libera calor a medida que alcanza el equilibrio se define como exotérmica, y la\(ΔH\) reacción exotérmica será negativa. Por ejemplo, un paquete dice que una barra de chocolate tiene 90 Calorías. Esto significa que al quemar la barra se generarán 90 kilocalorías (Kcal) de calor según se mide en el calorímetro. Recordemos que una Calorías (con una C mayúscula) = 1000 calorías, o una Kcal. Una caloría (minúscula) es la energía necesaria para elevar un gramo de agua en 1oC).
Probablemente estés más familiarizado con las reacciones que liberan calor, pero algunas reacciones químicas realmente absorben calor. Toma el paquete frío común del hospital por ejemplo. Apriétalo para ponerla en marcha y tírala en el calorímetro. ¡Puedes ver caer la temperatura en el calorímetro mientras el paquete absorbe el calor de los alrededores! Tales reacciones se definen como endotérmicas, con un positivo\(ΔH\). OK, para que podamos determinar el valor de uno de los parámetros energéticos... necesitamos conocer al menos uno al otro, ya sea\(ΔGo\) o\(ΔS\) antes de que la ecuación\(ΔH = ΔGo + TΔS\) se vuelva útil.
D. ¿Cómo se determina el Cambio Estándar de Energía Libre (\(ΔGo\))?
Resulta que el cambio estándar de energía libre,\(ΔGo\), es directamente proporcional a las concentraciones de reactivos y productos de una reacción conducida hasta su finalización (es decir, equilibrio) bajo condiciones estándar. Por lo tanto\(ΔGo\), para determinar, necesitamos poder medir la concentración de reactivos y productos de reacción antes y después de una reacción química (es decir, cuando la reacción alcanza el equilibrio). Tome la siguiente reacción química genérica:
\[2A + B <===> 2C + D\]
La siguiente ecuación relaciona\(ΔGo\) las concentraciones de equilibrio de A, B, C y D:
\[ΔGo = -RTlnKeq = -RTln((C^2+D)/(A^2+B))\]
R = la constante de gas (1.806 cal/mole-deg), T = 298OK y Keq es la constante de equilibrio. Esta es la ecuación de Boltzman. Como se puede ver, el Keq para la reacción es la relación del producto de las concentraciones de los productos (elevado a sus potencias estequiométricas) al producto de las concentraciones de los reactivos (elevado a sus potencias estequiométricas).
Si puede determinar concentraciones de equilibrio de reactivos y productos en una reacción química, puede usar esta ecuación para calcular\(ΔGo\) (cambio de energía libre estándar) para una reacción. Considere la siguiente reacción química genérica:
\[A + B ⇔ C + D\]
Si el\(ΔGo\) es un número negativo, la reacción se define como exergónica. Decimos que las reacciones exergónicas liberan energía libre. Si el\(ΔGo\) es un número positivo, la reacción absorbe energía libre y se define como endergónica.
E. Elaboración de un Ejemplo Usando Estas Ecuaciones para Sistemas Cerrados
Considera la siguiente reacción:
\[X ⇔ Y\]
Si te dan [X] e [Y], también puedes hacer las matemáticas. En equilibrio, se midieron (ensayaron) las concentraciones de los reactivos y productos para esta reacción, con los siguientes resultados:
[X] = 2.5 Kcal/Mole; [Y] = 500 Cal/mol
Utilice la ecuación de Boltzmann (anterior) para calcular la energía libre estándar para esta reacción. ¿Cuál es el Keq para esta reacción? ¿Cuál es el\(ΔGo\) para la reacción? Si no se te ocurrió un Keq de 0.2 y un valor absoluto para la energía libre estándar para |\(ΔGo\) | de 866.2 Kcal/mole, recalcula o colabora con un compañero de clase. Pista: ¡asegúrate de convertir las unidades en tu ecuación para que todas sean iguales!). Con base en el valor calculado de\(ΔGo\), ¿esta reacción es endergónica o exergónica?
Si realiza la reacción en un calorímetro de bomba, procede al equilibrio con a\(ΔH\) = -750 Kcal/Mole. ¿Qué tipo de reacción es esta? Junto con el cambio de entalpía, ahora es posible calcular un valor absoluto para que el cambio de entropía sea |\(ΔS\) | = 116.2 cal/mol-deg para esta reacción. En equilibrio, ¿la reacción procedió con un aumento o disminución de la entropía en condiciones estándar? Nuevamente, si no obtuviste la respuesta correcta, vuelve a calcular o colaborar con un compañero de clase.
F. Resumen: Las propiedades de los sistemas cerrados
Primero, reiteremos que no existe tal cosa como un sistema cerrado, ¡a menos que por supuesto que el universo sea uno! Lo que llamamos un sistema cerrado es simplemente uno en el que podemos medir la energía que entra o sale del sistema, y dentro del cual podemos medir las transferencias y transducciones de energía (cambios de un tipo de energía a otro.
Las características de los sistemas se pueden definir por sus propiedades:
Propiedades de Sistemas Cerrados
- Los sistemas cerrados son definidos experimentalmente por un investigador.
- Aplican condiciones estándar.
- La energía que entra o sale del sistema es medible.
- Las reacciones alcanzan el equilibrio independientemente de la velocidad de reacción.
- Las concentraciones de producto y reactivo en equilibrio son constantes.
- Los valores medidos de transferencia/transducción de energía son constantes.
G. Cambio Real de Energía Libre en Sistemas Abiertos
Posteriormente estaremos discutiendo el flujo de energía a través de los seres vivos, desde la luz solar hasta la energía química en las moléculas de nutrientes en ATP, desde la energía química como ATP hasta la realización de todo tipo de trabajo celular. Las células son sistemas abiertos que constantemente intercambian masa y energía con su entorno y nunca alcanzan el equilibrio. Además, diversos organismos viven bajo condiciones atmosféricas muy diferentes y mantienen diferentes temperaturas corporales (por ejemplo, ¡tu gato tiene una temperatura corporal más alta que tú!). Claramente, las condiciones bajo las cuales las células conducen sus reacciones bioquímicas son decididamente no estándar. Sin embargo, si bien los sistemas abiertos no alcanzan el equilibrio, sí logran un estado estacionario en el que la tasa de entrada de energía y materia es igual a la tasa de salida de energía y materia. Piense en una vía bioquímica como la glucólisis. Si las necesidades energéticas de una célula son constantes, el camino alcanzará un estado estacionario. Por supuesto, la necesidad de energía de una célula (como ATP) puede cambiar a medida que cambian las necesidades energéticas. Si lo hace, entonces el estado estacionario de la producción de ATP cambiará para satisfacer las necesidades de la célula.
Dado que las velocidades de reacción pueden cambiar (y de hecho están reguladas en las células), lo que implica que el estado estacionario de una reacción o vía bioquímica puede cambiar. Caracterizamos los sistemas abiertos por sus propiedades, como se indica a continuación.
Propiedades de Sistemas Abiertos
- Los sistemas abiertos intercambian energía y masa con su entorno.
- Los sistemas abiertos nunca alcanzan el equilibrio
- Alcanzan estado estacionario donde la tasa de entrada de energía = tasa de salida.
- El estado estacionario puede cambiar.
- En sistemas abiertos, las reacciones endergónicas pueden ser energéticamente favorables (espontáneas).
Afortunadamente, existe una ecuación para determinar los cambios de energía libre en sistemas abiertos. Para nuestra reacción química\(2A + B <===> 2C + D\), esta ecuación sería:
\[ΔG' = ΔGo + RT\ln(((Css)^2+Dss)/((Ass)^2+Bss))\]
Aquí,\(ΔG'\) está el cambio real de energía libre para una reacción en un sistema abierto. \(ΔGo\)es el cambio estándar de energía libre para la misma reacción en condiciones estándar. En un sistema cerrado. R es nuevamente la constante del gas (1.806 cal/mole-deg) y T es la temperatura absoluta en la que realmente se está produciendo la reacción. El subíndice 'ss' designa las concentraciones de reactivo y producto medidas en condiciones de estado estacionario. Para determinar la energía libre real de una reacción bioquímica en una célula (de hecho en cualquier tejido vivo), todo lo que necesita saber es la de la\(ΔGo\) reacción, las concentraciones en estado estacionario de los componentes de la reacción en las células/tejidos, y la T absoluta bajo la cual se producen las reacciones.
144 La Energética de los Sistemas Abiertos
En otros lugares, utilizaremos las reacciones de la vía glicolítica para ejemplificar la energética de los sistemas abiertos y cerrados. En ese momento, prestar especial atención a la aplicación de la terminología energética en la descripción del flujo de energía en sistemas cerrados vs. abiertos.