1.1: Evaluación de la pendiente del terreno
- Page ID
- 52748
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Aquí, en el noroeste del Pacífico, tenemos la suerte de trabajar en un paisaje de variados accidentes geográficos, desde picos volcánicos hasta amplios valles; desde laderas empinadas y boscosas hasta sabanas suavemente onduladas; desde arroyos de montaña en rápida cascada hasta serpenteantes llanuras aluviales fluviales. Nuestra variada topografía es parte integral de nuestros ecosistemas forestales, influyendo en nuestro clima, suelos, agua, vida vegetal y hábitat de peces (Figura 1.1). Como técnicos de recursos naturales, a menudo se nos llama a evaluar la topografía, y uno de los elementos comunes que medimos es la pendiente del terreno. ¿Qué tan empinada es la ladera? ¿La pendiente drena a un arroyo? ¿Hay acantilados o acantilados presentes? Los datos de campo recopilados por los técnicos conducen a decisiones informadas sobre las actividades de manejo de la tierra, como proporcionar sombra para arroyos, construir caminos o senderos y prescribir operaciones de manejo de madera.

Figura 1.1. El Tenedor fangoso del río Sandy se origina en campos de nieve en el flanco oeste del monte. Campana, transportando gravas gruesas y arena aguas abajo. Los suelos finos de las laderas empinadas y boscosas circundantes también bajan por la pendiente hasta el río.
Definición de Talud
La pendiente del terreno es esencialmente el gradiente o inclinación del terreno. Una pendiente pronunciada se refiere a una pendiente pronunciada; una pendiente suave se refiere a una ligera pendiente. Las empinadas laderas boscosas de la Figura 1.1 contrastan con la pendiente más suave del camino del río a medida que fluye entre ellas.
Al conducir por una autopista, es posible que vea una señal de tráfico que dice “6% Grado” o “pendiente empinada”. El grado de la carretera es esencialmente la pendiente de la carretera. El letrero de la Figura 1.2 indica que el camino desciende a una pendiente del 6% o a una pendiente del 6%.
Figura 1.2. Una señal vial que indique una pendiente de 8%, o 8% de pendiente. (www.dot.state.co.us)
Una pendiente del 6% significa que la elevación de la carretera cambia 6 pies por cada 100 pies de distancia horizontal (Figura 1.3).

Figura 1.3. Una carretera sube con una pendiente del 6%. La carretera gana 6 pies de elevación por cada 100 pies de distancia horizontal. Tenga en cuenta que la longitud de la carretera en sí es superior a 100 pies.
Matemáticamente, la pendiente se define como “la subida sobre la carrera” (o la subida dividida por la carrera), donde la subida es igual al cambio en la elevación y la carrera es igual a la distancia horizontal:
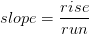
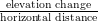 o en este caso:
o en este caso: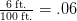
Para expresar la pendiente como una pendiente porcentual, simplemente multiplicamos la fracción de pendiente por 100. Entonces, .06 = 6%
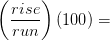 %talud
%talud
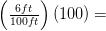 6%
6%
En nuestro ejemplo vial, el cambio de elevación de seis pies es la subida y la distancia horizontal de 100 pies de la carretera es la carrera. Conduciendo cuesta arriba, subimos una pendiente de +6% (Figura A abajo). Al conducir cuesta abajo, la “subida” es en realidad una “caída”, así que tenemos una pendiente negativa, o una pendiente cuesta abajo (Figura B a continuación). Cuando se trata de pendiente, una pendiente positiva simplemente significa cuesta arriba y una pendiente negativa significa cuesta abajo. Un número negativo no significa “menos” como en las expresiones algebraicas.
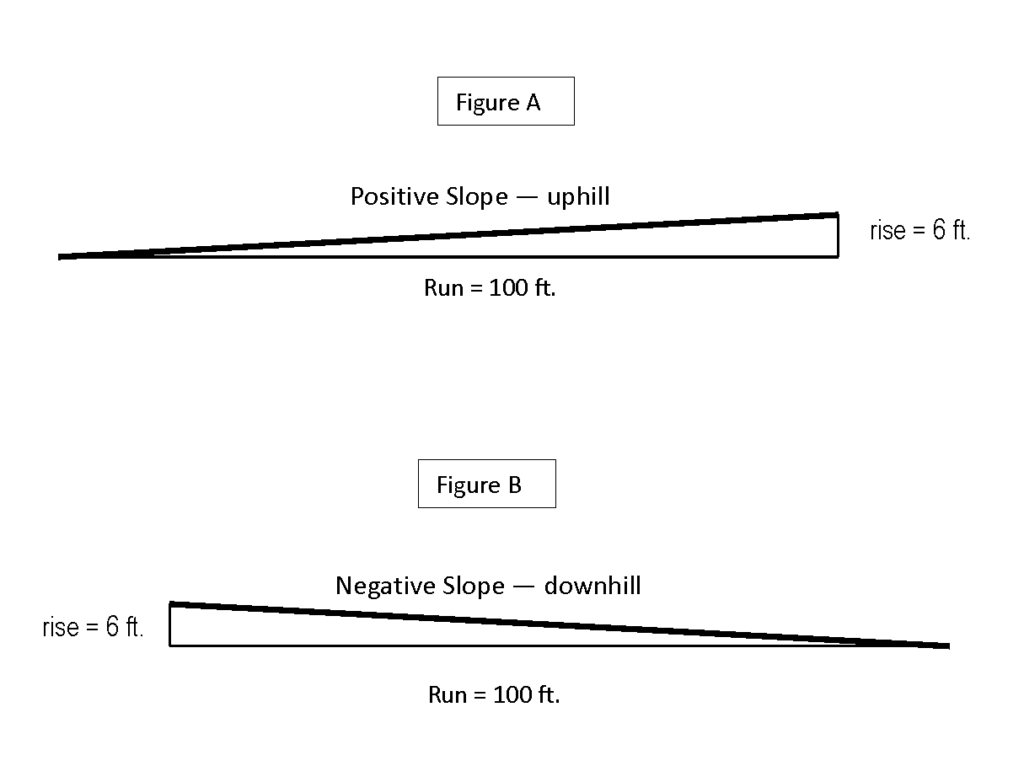
Tenga en cuenta que la distancia real de la carretera es la hipotenusa del triángulo de pendiente ilustrado. Su longitud se llama distancia de pendiente. La distancia de pendiente es siempre más larga que la distancia horizontal, o recorrido. Aplicando el Teorema de Pitágoras (a 2 + b 2 = c 2) a este triángulo, podemos calcular la distancia de pendiente, o hipotenusa (c).
a 2 + b 2 = c 2 donde: 100 2 + 6 2 = c 2 10,036 = c 2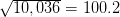 ft.
ft.
a = distancia horizontal o recorrido (en este ejemplo 100 ft.)
b= cambio en la elevación o subida (en este ejemplo 6 ft.)
c = distancia de carretera o distancia de pendiente (en este ejemplo 100.2 ft.)
Calculamos una distancia de pendiente de 100.2 pies para una carrera de 100 pies. Como se puede ver en este ejemplo, en un bosque, una pendiente del 6% se consideraría una pendiente suave.
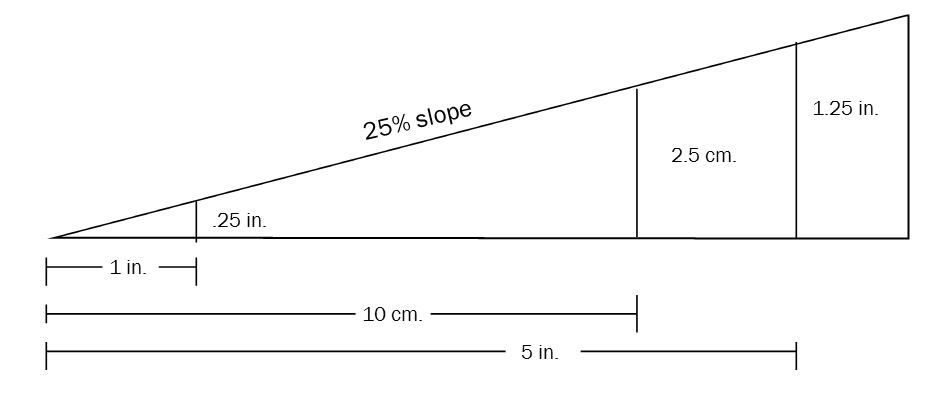
Tenga en cuenta que el% de pendiente no es unitario y proporcional. Por lo tanto, se puede aplicar a cualquier unidad de medida (pulgadas, yardas, centímetros, etc.) y a cualquier longitud. Por ejemplo, una pendiente del 25% es simplemente una relación 25:100. La pendiente del 25% a continuación muestra que por cada pulgada de distancia horizontal, la pendiente se eleva .25 pulgadas. Por cada 10 centímetros de distancia horizontal, la pendiente sube 2.5 cm, y por cada 5 pulgadas de distancia horizontal, sube 1.25 pulgadas.
Uso de talud
Al escribir notas de campo sobre un sitio, incluimos información sobre la pendiente del terreno. A veces es suficiente una estimación aproximada de la pendiente promedio; a veces se requieren mediciones detalladas de la pendiente. Por ejemplo, una descripción del sitio podría decir:
“Se realizó un crucero maderero sobre 20 acres de bosque mixto de coníferas... Aproximadamente la mitad de la superficie era plana, en pendientes que oscilaban entre 3-7%. La otra mitad de la superficie fue más pronunciada; con pendientes suroeste 40-60%”.
Esto nos dice mucho más sobre el sitio que simplemente afirmar que había 20 acres de bosque mixto. Se esperaría que diferentes condiciones de suelo y vegetación diferente estuvieran presentes en las diferentes laderas, y por lo tanto, tal vez diferente manejo. Digamos, por ejemplo, que estos 20 acres van a ser registrados en un futuro próximo. Si esto es así, el silvicultor deberá planear dónde colocar nuevas vías de acceso, dónde ubicar los aterrizajes para yardar los troncos y qué tipo de equipo de cosecha utilizar. Sabe que la pendiente de cualquier carretera nueva de espolón no debe superar el 10%, y se debe utilizar un sistema de cable para transportar troncos hasta aterrizajes en pendientes superiores al 30% (Figura 1.4).
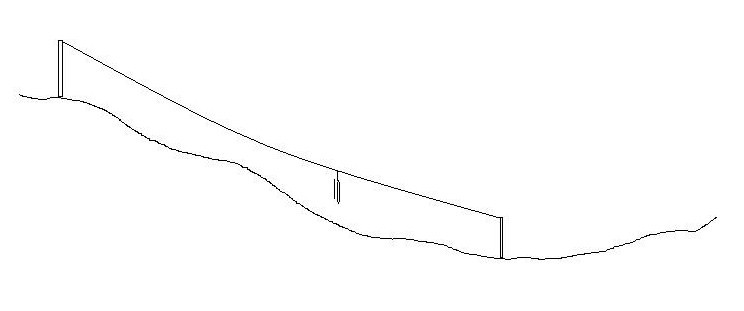
Figura 1.4. Un sistema de registro de cable se puede utilizar en pendientes empinadas para suspender troncos sobre el suelo a medida que “astillan” los troncos por la pendiente hasta un rellano.
Los profesores pueden correr para obtener una imagen detallada de la pendiente. Al perfilar una ladera, se toman las distancias de talud y las lecturas de %talud donde ocurre cada cambio importante en la pendiente (Figura 1.5). Con esta información precisa, se puede diseñar un sistema de tala que levantará troncos del suelo mientras se lidera para reducir la erosión.
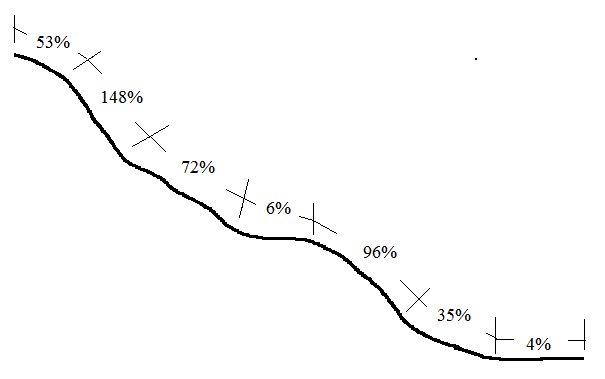
Figura 1.5. Una ladera se divide en segmentos donde ocurren cambios importantes en la pendiente. Para cada segmento, se toma una lectura de %pendiente. Estos %lecturas se combinan con mediciones de la distancia de pendiente para cada segmento para crear un perfil o boceto del cerro como el ilustrado.
Tenga en cuenta que las pendientes pueden superar el 100%. Cuando una pendiente es igual al 100%, simplemente significa que la subida es igual a la carrera. Y aunque ciertamente se siente como si estuvieras escalando recto en una pendiente del 100% (levantándote usando raíces y cualquier otra cosa que puedas agarrar), realmente estás caminando hacia arriba en un ángulo de 45°, no un ángulo de 90°.
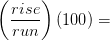 %talud
%talud
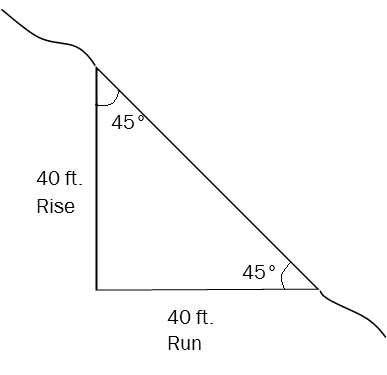
Si subida = correr como se ilustra arriba: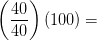 100%
100%
100% de pendiente = ángulo de inclinación de 45º
Otros ejemplos de donde se mide el% de pendiente en entornos de recursos naturales incluyen rutas de senderismo y arroyos. Los retrocesos en pendientes empinadas reducen la erosión del sendero y facilitan el senderismo. Algunos senderos se mantienen al 8% para cumplir con las pautas de la Ley Americana con Discapacidades (ADA) para el acceso a sillas de ruedas.
Los gradientes de los arroyos varían, reflejando el terreno sobre el que fluyen en cada etapa de su viaje a grandes ríos. Los afluentes pequeños suelen ser los más empinados, cayendo en cascada por empinadas laderas boscosas en pendientes de 60-100% o más. A medida que los arroyos se fusionan río abajo, el terreno a menudo se aplana y se pueden medir gradientes más suaves de 3-10% de pendiente (Figura 1.6).

Figura 1.6. Los arroyos se precipitan por pendientes pronunciadas en sus cabeceras. A medida que llegan al fondo del valle y se funden con otros arroyos, sus gradientes se reducen y puede resultar una ruta más serpenteante.


