2.3: Uso de la pendiente porcentual para determinar la altura del árbol
- Page ID
- 52825
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.3 Uso de la pendiente porcentual para determinar la altura del árbol
Cuando se utiliza la pendiente porcentual para determinar la altura del árbol, el árbol es la subida, y la distancia horizontal desde el árbol a lo largo del suelo es la carrera (Figura 2.3). Podemos medir fácilmente nuestra distancia horizontal desde el árbol, y tenemos instrumentos para medir el porcentaje de pendiente hasta la cima de un árbol. Entonces, con esas dos medidas (carrera y %pendiente) podemos resolver para subida.
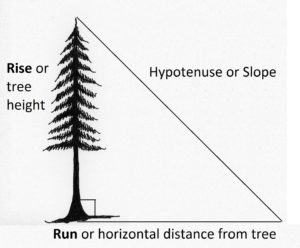
Figura 2.3. Un árbol hace un ángulo recto con el suelo, por lo que se puede dibujar un triángulo o pendiente usando él y el suelo.
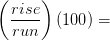%pendiente
Para resolver la ecuación %slope para “rise” hacemos lo siguiente:
1. Multiplica ambos lados de la ecuación por “run” para cancelar la ejecución en el lado izquierdo de la ecuación
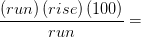(ejecución) (%pendiente)
2. Divide ambos lados por “100” para cancelar 100 en el lado izquierdo de la ecuación
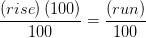(% pendiente)
Eso nos deja con la siguiente ecuación:
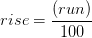(%pendiente) donde subida =altura
Observe que el multiplicador de pendiente% (100) se convierte en el denominador. Esto sigue siendo una constante. Los valores de recorrido y %pendiente son medidas, por lo que cambiarán con cada árbol.
Aquí hay algunos ejemplos usando %slope para la altura del árbol:
Ejemplo 1:
Georgia sale a una distancia horizontal de 50 pies de un árbol (Figura 2.4). Ella mira a través de su clinómetro para determinar el% de pendiente desde su ojo hasta la cima del árbol. Mirando hacia arriba, lee “+124%”. Usando nuestra fórmula para determinar el “ascenso”:
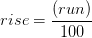(% pendiente)
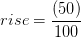(+124) = +62 o 62 pies
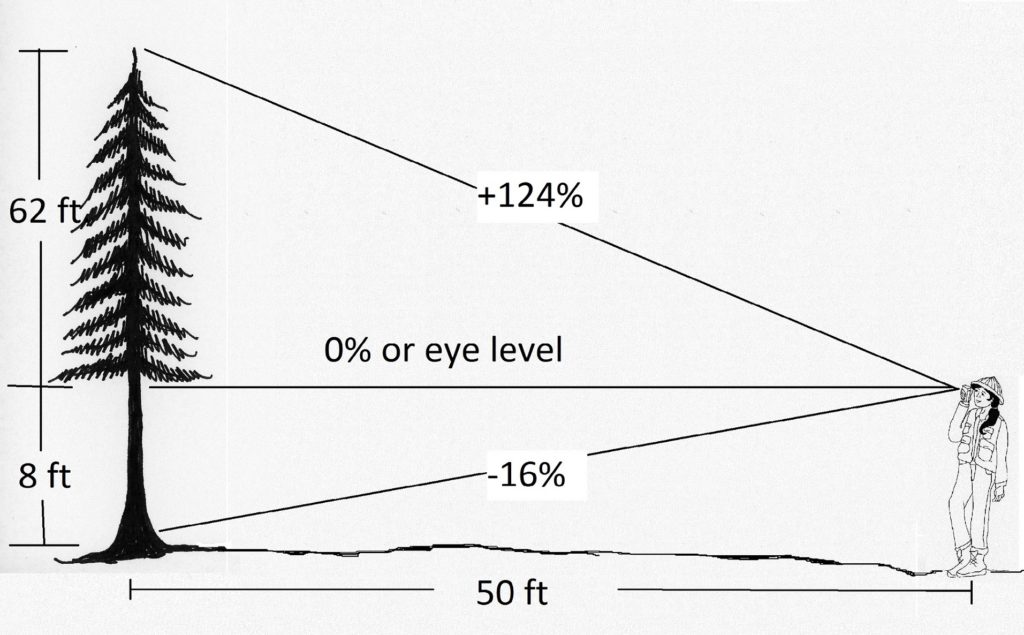
Figura 2.4. Usando un clinómetro y% de pendiente para determinar la altura total del árbol.
Por lo tanto, la altura del árbol desde su ojo hasta la cima es de 62 pies. A continuación, utilizamos el mismo procedimiento para determinar la altura desde el nivel del ojo de Georgia hasta el tocón. Georgia lleva una lectura hasta el tocón. Ella lee -16%.
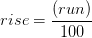(% pendiente)
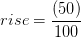(-16) = -8 o 8 pies
Georgia medía 62 pies desde su ojo hasta la cima del árbol, y 8 pies desde su ojo hasta el tocón del árbol. Agregamos esas dos medidas juntas para obtener la altura total del árbol.
62 pies (arriba) + 8 pies (base) = 70 pies.
Recuerda que una medición de pendiente negativa simplemente significa que estás mirando cuesta abajo. Es importante reconocer que el -8 pies es una caída en la elevación, no un valor negativo.
Podemos hacer los dos cálculos en un solo paso de la siguiente manera:
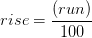(% pendiente)
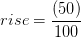(124+16) = 70 o 70 pies
Observe que Georgia puso “+16” en la fórmula, a pesar de que la lectura al tocón fue un número negativo. Ella quiere sumar en la altura inferior, no restarla. Nuevamente, una pendiente negativa simplemente significa que miramos cuesta abajo. Tienes que pensar en la posición de tu ojo en relación con el árbol, y lo que realmente significan las lecturas. Usar símbolos %slope algebraicamente puede ser engañoso.
Ejemplo 2:
Tobías sale a una distancia horizontal de 100 pies del mismo árbol (Figura 2.5). Él mira a la parte superior del árbol y lee “+62%” en su clinómetro. Él mira hacia el tocón y lee “-8”.
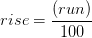(% pendiente)
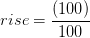(62+8) = 70 o 70 pies
Observe que al caminar más lejos del árbol (tener una carrera más larga), las lecturas de la pendiente de Tobías fueron más pequeñas que las de Georgia, a pesar de que ambas terminaron con la misma altura. Los ángulos en los que Tobías miraba el árbol eran más pequeños (menos agudos).
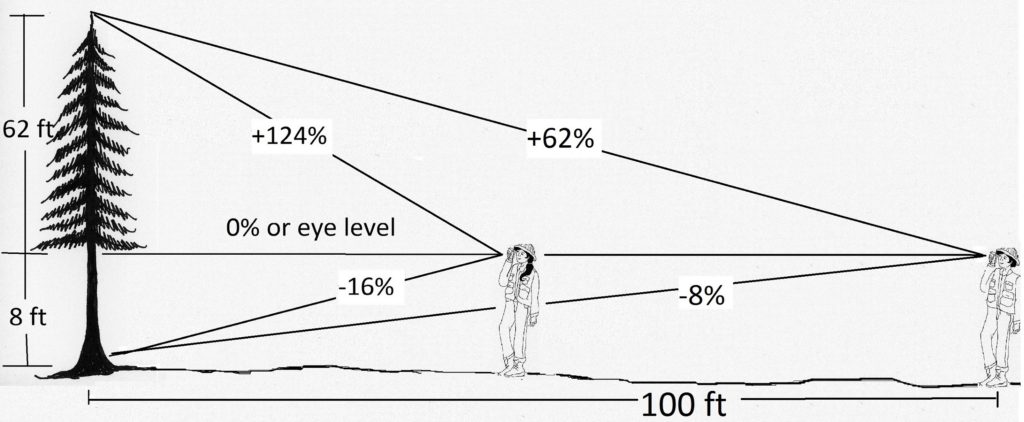
Figura 2.5. Un árbol se puede medir desde cualquier distancia, pero cuanto más atrás esté el árbol, menos acortada será la vista y, en general, más precisas serán las lecturas de pendiente.
También fíjese que cuando Tobías salió a 100 pies del árbol, su carrera igualó al denominador, 100, cancelándolo y dejando el árbol igual a las lecturas de los clinómetros. Este “atajo” hace que sea mucho más fácil y rápido determinar la altura del árbol al reducir el número de conversiones que se tienen que hacer.
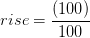(62+8) = 70 o 70 pies
¿Qué sucede a una distancia horizontal de 150 pies? Las lecturas de pendiente son aún más pequeñas.
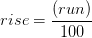(% pendiente)
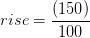(42+5) = 70 o 70 pies
Así, cuanto más lejos se camina del árbol, mejor es la perspectiva para ver la cima del árbol. Estar demasiado cerca del árbol puede resultar en una parte superior oscurecida, ya que las ramas laterales estarán en el camino (Figura 2.6).
En la foto de la izquierda se ve claramente la parte superior del árbol. La foto de la derecha, sin embargo, ilustra una vista acortada de la parte superior donde las ramas laterales podrían confundirse con la parte superior.
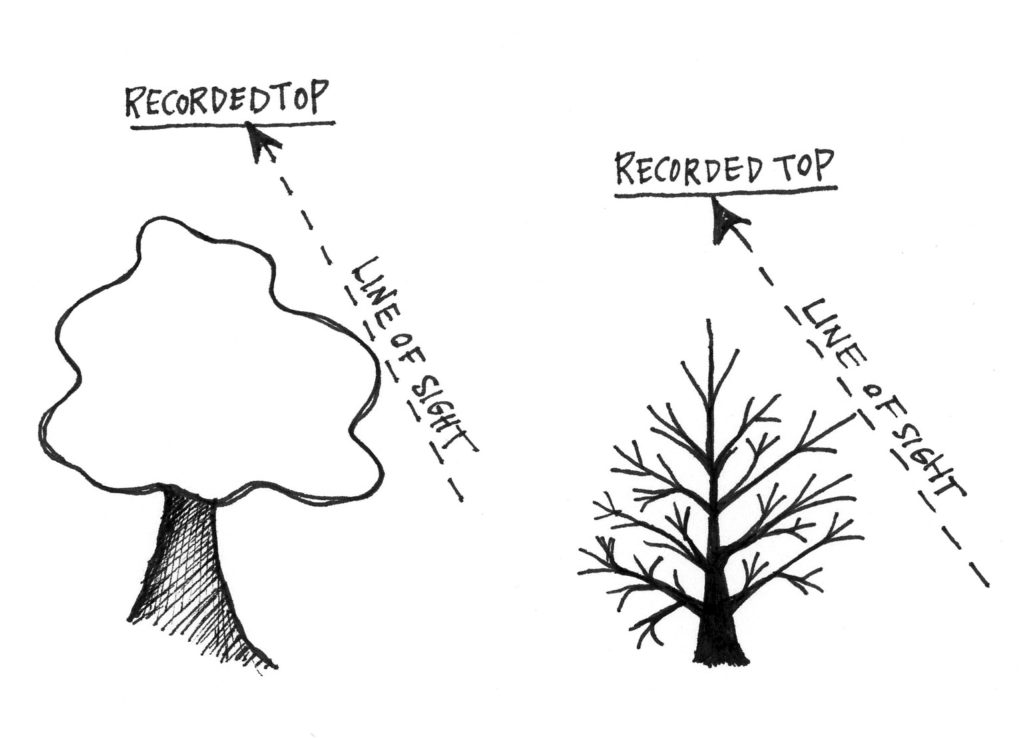
Figura 2.6. Ejemplos de error de medición de altura por avistamiento en una rama lateral que se cree que es la parte superior, tanto en una madera dura como en una conífera. La altura está sobreestimada.