4.2: Crecimiento y Regulación de la Población
- Page ID
- 52704
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los ecologistas poblacionales utilizan diversos métodos para modelar la dinámica poblacional. Un modelo preciso debe ser capaz de describir los cambios que ocurren en una población y predecir cambios futuros. Los dos modelos más simples de crecimiento poblacional utilizan ecuaciones deterministas (ecuaciones que no dan cuenta de eventos aleatorios) para describir la tasa de cambio en el tamaño de una población a lo largo del tiempo. El primero de estos modelos, el crecimiento exponencial, describe poblaciones que aumentan en número sin ningún límite para su crecimiento. El segundo modelo, el crecimiento logístico, introduce límites al crecimiento reproductivo que se vuelven más intensos a medida que aumenta el tamaño de la población. Ninguno de los modelos describe adecuadamente a las poblaciones naturales, pero proporcionan puntos de comparación.
Crecimiento Exponencial
Charles Darwin, al desarrollar su teoría de la selección natural, fue influenciado por el clérigo inglés Thomas Malthus. Malthus publicó su libro en 1798 afirmando que las poblaciones con abundantes recursos naturales crecen muy rápidamente. Sin embargo, limitan un mayor crecimiento al agotar sus recursos. El patrón temprano de acelerar el tamaño de la población se llama crecimiento exponencial (Figura\(\PageIndex{1}\)).
El mejor ejemplo de crecimiento exponencial en organismos se observa en bacterias. Las bacterias son procariotas que se reproducen rápidamente, alrededor de una hora para muchas especies. Si se colocan 1000 bacterias en un matraz grande con abundante aporte de nutrientes (por lo que los nutrientes no se agotarán rápidamente), el número de bacterias se habrá duplicado de 1000 a 2000 después de apenas una hora. En otra hora, cada una de las 2000 bacterias se dividirá, produciendo 4000 bacterias. Después de la tercera hora, debería haber 8000 bacterias en el matraz. El concepto importante de crecimiento exponencial es que la tasa de crecimiento —el número de organismos añadidos en cada generación reproductiva— está aumentando en sí misma; es decir, el tamaño de la población está aumentando a un ritmo cada vez mayor. Después de 24 de estos ciclos, la población habría aumentado de 1000 a más de 16 mil millones de bacterias. Cuando el tamaño de la población, N, se traza a lo largo del tiempo, se produce una curva de crecimiento en forma de J (Figura\(\PageIndex{1}\)).
El ejemplo de bacterias en un matraz no es realmente representativo del mundo real donde los recursos suelen ser limitados. Sin embargo, cuando una especie se introduce en un nuevo hábitat que encuentra adecuado, puede mostrar un crecimiento exponencial por un tiempo. En el caso de las bacterias en el matraz, algunas bacterias morirán durante el experimento y así no se reproducirán; por lo tanto, la tasa de crecimiento se reduce de una tasa máxima en la que no hay mortalidad.
Crecimiento Logístico
El crecimiento exponencial extendido sólo es posible cuando se dispone de infinitos recursos naturales; este no es el caso en el mundo real. Charles Darwin reconoció este hecho en su descripción de la “lucha por la existencia”, que establece que los individuos competirán, con miembros de su propia u otra especie, por recursos limitados. Los exitosos tienen más probabilidades de sobrevivir y transmitir los rasgos que los hicieron exitosos a la siguiente generación a un ritmo mayor (selección natural). Para modelar la realidad de los recursos limitados, los ecologistas poblacionales desarrollaron el modelo de crecimiento logístico.
Capacidad de carga y modelo logístico
En el mundo real, con sus limitados recursos, el crecimiento exponencial no puede continuar indefinidamente. El crecimiento exponencial puede ocurrir en entornos donde hay pocos individuos y abundantes recursos, pero cuando el número de individuos sea lo suficientemente grande, los recursos se agotarán y la tasa de crecimiento disminuirá. Eventualmente, la tasa de crecimiento se estabilizará o nivelará (Figura\(\PageIndex{1}\)). Este tamaño poblacional, que está determinado por el tamaño máximo de población que puede sostener un ambiente en particular, se denomina capacidad de carga, simbolizada como K. En poblaciones reales, una población en crecimiento suele rebasar su capacidad de carga y la tasa de mortalidad aumenta más allá de la tasa de natalidad provocando que el tamaño de la población disminuya de nuevo a la capacidad de carga o por debajo de ella La mayoría de las poblaciones suelen fluctuar alrededor de la capacidad de carga de manera ondulada en lugar de existir justo en ella.
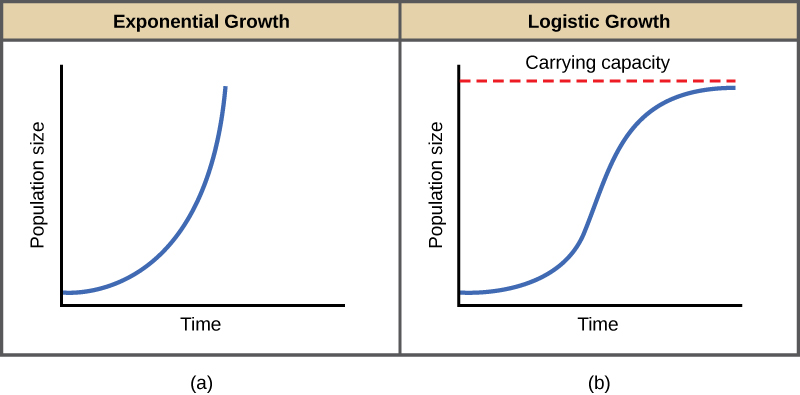
Una gráfica de crecimiento logístico produce la curva en forma de S (Figura\(\PageIndex{1}\)). Se trata de un modelo más realista de crecimiento poblacional que de crecimiento exponencial. Hay tres secciones diferentes a una curva en forma de S. Inicialmente, el crecimiento es exponencial porque hay pocos individuos y amplios recursos disponibles. Entonces, a medida que los recursos comienzan a limitarse, la tasa de crecimiento disminuye. Finalmente, la tasa de crecimiento se nivela en la capacidad de carga del ambiente, con poco cambio en el número de población a lo largo del tiempo.
Ejemplos de Crecimiento Logístico
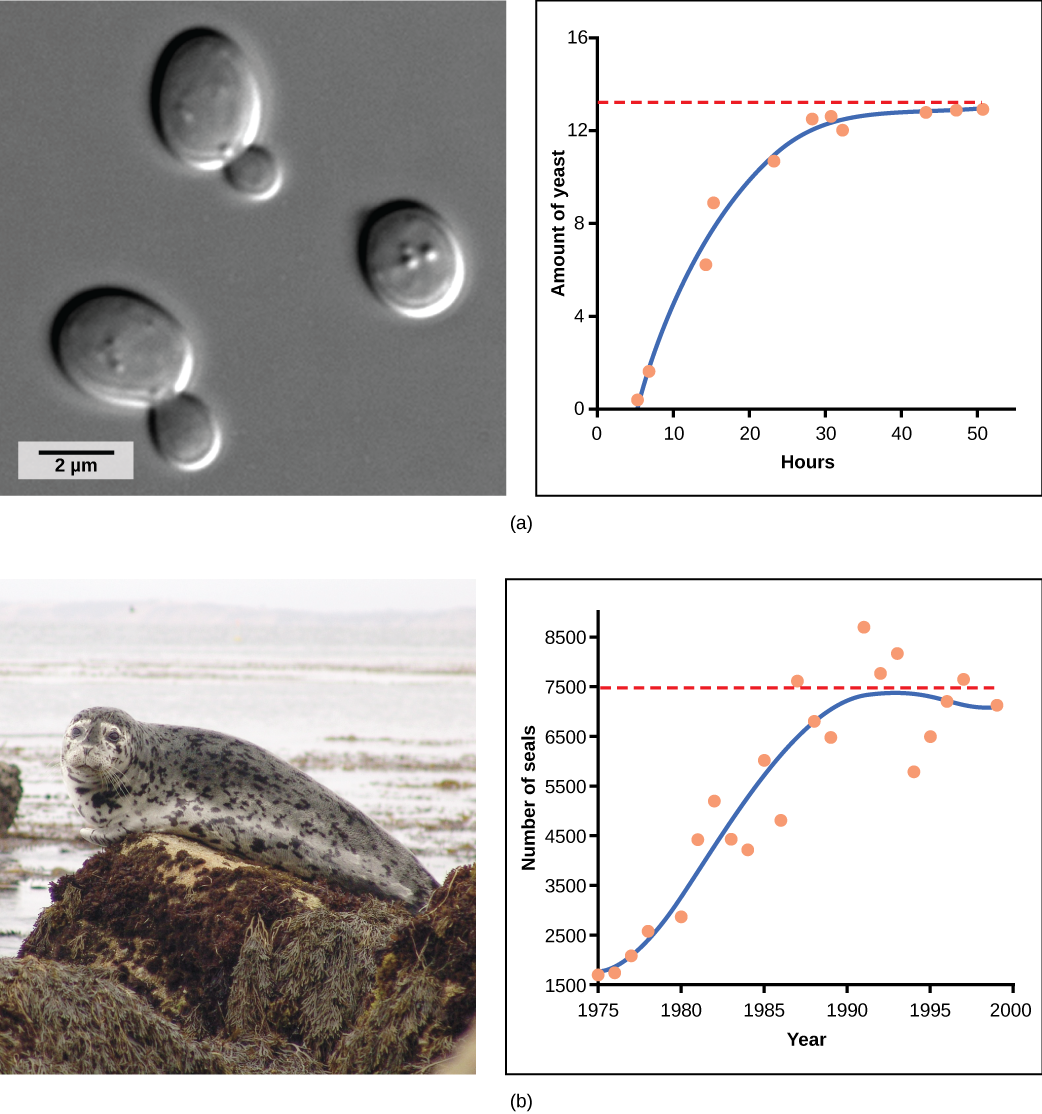
La levadura, un hongo unicelular utilizado para hacer pan y bebidas alcohólicas, exhibe la curva clásica en forma de S cuando se cultiva en un tubo de ensayo (Figura\(\PageIndex{2}\) a). Su crecimiento se nivela a medida que la población agota los nutrientes necesarios para su crecimiento. En el mundo real, sin embargo, hay variaciones a esta curva idealizada. Los ejemplos en poblaciones silvestres incluyen ovejas y focas de puerto (Figura\(\PageIndex{2}\) b). En ambos ejemplos, el tamaño de la población supera la capacidad de carga por cortos periodos de tiempo y luego cae por debajo de la capacidad de carga posteriormente. Esta fluctuación en el tamaño de la población continúa ocurriendo a medida que la población oscila alrededor de su capacidad de carga. Aún así, incluso con esta oscilación se confirma el modelo logístico.
Dinámica y Regulación Poblacional
El modelo logístico de crecimiento poblacional, si bien es válido en muchas poblaciones naturales y un modelo útil, es una simplificación de la dinámica poblacional del mundo real. Implícito en el modelo es que la capacidad de carga del entorno no cambia, lo que no es el caso. La capacidad de carga varía anualmente. Por ejemplo, algunos veranos son calurosos y secos mientras que otros son fríos y húmedos; en muchas zonas, la capacidad de carga durante el invierno es mucho menor que durante el verano. Además, eventos naturales como sismos, volcanes e incendios pueden alterar un ambiente y de ahí su capacidad de carga. Adicionalmente, las poblaciones no suelen existir aisladas. Comparten el ambiente con otras especies, compitiendo con ellas por los mismos recursos (competencia interespecífica). Estos factores también son importantes para entender cómo crecerá una población específica.
¿Por qué se extinguió el mamut lanudo?
La mayoría de las poblaciones de mamuts lanudos se extinguieron hace unos 10 mil años, poco después los paleontólogos creen que los humanos comenzaron a colonizar América del Norte y el norte de Eurasia (Figura\(\PageIndex{3}\)). Una población mamut sobrevivió en la isla Wrangel, en el mar de Siberia Oriental, y fue aislada del contacto humano hasta tan recientemente como 1700 a.C. Sabemos mucho de estos animales a partir de cadáveres encontrados congelados en el hielo de Siberia y otras regiones del norte.

Comúnmente se piensa que el cambio climático y la caza humana llevaron a su extinción. Un estudio de 2008 estimó que el cambio climático redujo el rango del mamut de 3.000.000 de millas cuadradas hace 42,000 años a 310,000 millas cuadradas hace 6,000 años. 2 A través de evidencias arqueológicas de sitios de matanza, también está bien documentado que los humanos cazaban a estos animales. Un estudio de 2012 concluyó que ningún factor fue el responsable exclusivo de la extinción de estas magníficas criaturas. 3 Además del cambio climático y la reducción del hábitat, los científicos demostraron que otro factor importante en la extinción del mamut fue la migración de cazadores humanos a través del Estrecho de Bering hacia América del Norte durante la última edad de hielo hace 20 mil años.
El mantenimiento de poblaciones estables fue y es muy complejo, con muchos factores que interactúan determinando el desenlace. Es importante recordar que los humanos también son parte de la naturaleza. Una vez contribuimos al declive de una especie utilizando únicamente tecnología de caza primitiva.
Modelos Demográficos de Población
Los ecologistas poblacionales han planteado la hipótesis de que conjuntos de características pueden evolucionar en especies que conducen a adaptaciones particulares a sus entornos. Estas adaptaciones impactan el tipo de crecimiento poblacional que experimentan sus especies. Las características de la historia de vida como las tasas de natalidad, la edad en la primera reproducción, el número de crías e incluso las tasas de mortalidad evolucionan como la anatomía o el comportamiento, lo que lleva a adaptaciones que afectan el crecimiento Los ecologistas poblacionales han descrito un continuo de “estrategias” de historia de vida con especies seleccionadas por K en un extremo y especies seleccionadas por r en el otro. Las especies seleccionadas por K se adaptan a ambientes estables y predecibles. Las poblaciones de especies seleccionadas por K tienden a existir cerca de su capacidad de carga. Estas especies tienden a tener descendencia más grande, pero menor, y aportan grandes cantidades de recursos a cada descendencia. Los elefantes serían un ejemplo de una especie seleccionada por K. Las especies seleccionadas por r se adaptan a ambientes inestables e impredecibles. Tienen un gran número de crías pequeñas. Los animales seleccionados por r no proporcionan muchos recursos ni cuidado parental a la descendencia, y las crías son relativamente autosuficientes al nacer. Ejemplos de especies seleccionadas por r son invertebrados marinos como medusas y plantas como el diente de león. Las dos estrategias extremas se encuentran en dos extremos de un continuo en el que existirán historias de vida de especies reales. Además, las estrategias de historia de vida no necesitan evolucionar como suites, sino que pueden evolucionar independientemente unas de otras, por lo que cada especie puede tener algunas características que tienden hacia un extremo u otro.
Colaboradores y Atribuciones
- Dinámica y Regulación de la Población por OpenStax está licenciado bajo CC BY 4.0. Modificado del original por Matthew R. Fisher.


