Saltar al contenido principal
LibreTexts Español

1.10: Práctica - Cuadrados de Punnett y probabilidad

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    57577

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Consulta\(\PageIndex{1}\)

    Solución paso a paso

    1. Debido a que aquí hay dos rasgos, debemos realizar un cruce dihíbrido. Conocemos los genotipos progenitores (rrss y RRSS), pero necesitamos averiguar cuáles son los gametos posibles averiguando todas las combinaciones posibles de los dos alelos.

      Para la madre rrss, la única combinación posible de gametos es rs.

      Para el padre RRSS, la única combinación posible de gametos es RS.

    2. A continuación realizaremos el cruce dihíbrido.

      Cruz: rrss x RRSS

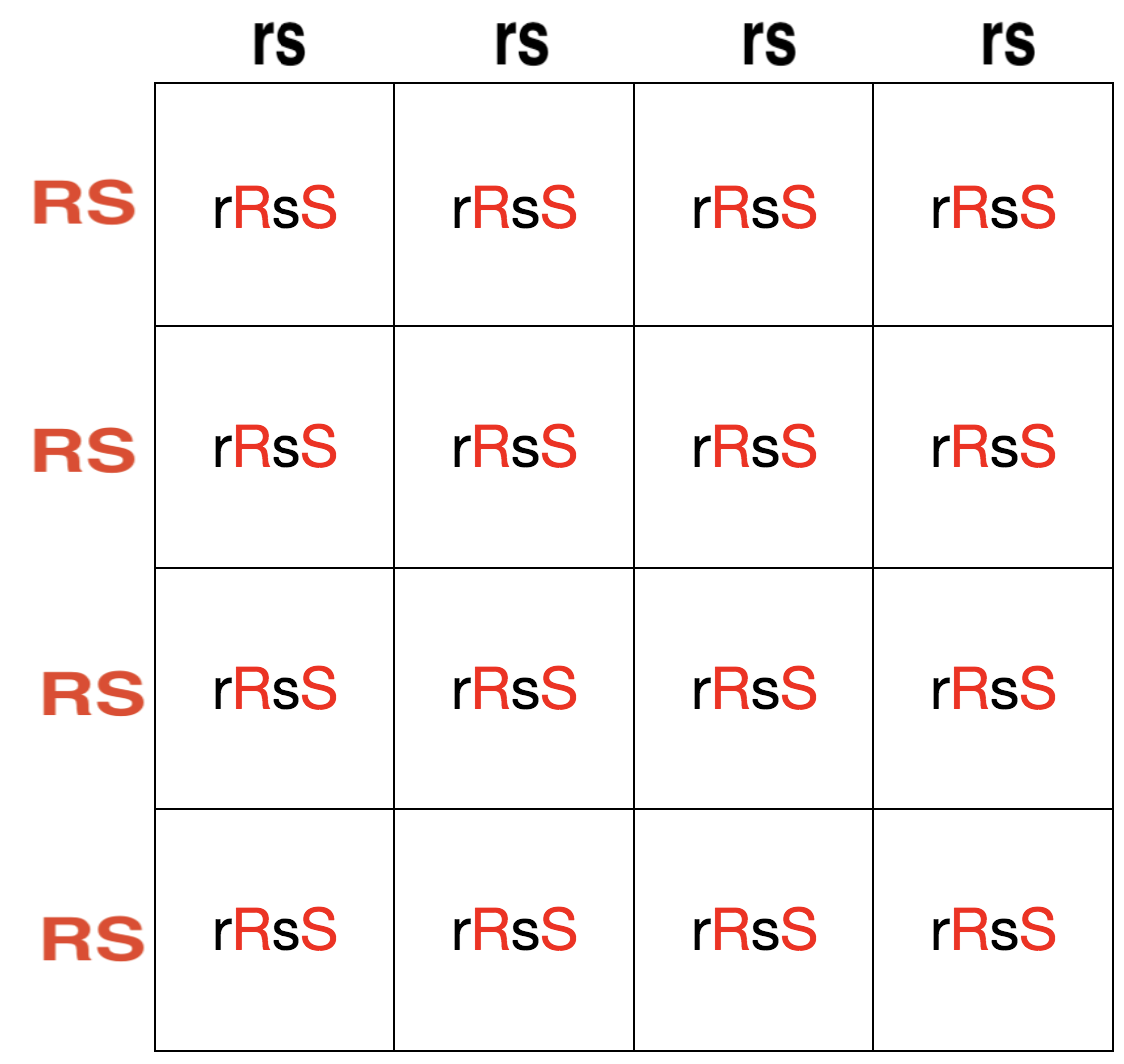
      Configuración cuadrada de Punnett dihíbrida que muestra proporciones de genotipos de un cruce rrss x RRSS

      Si completamos el cruce, encontramos que la posible descendencia solo puede ser RsSR. Los descendientes que tienen al menos un alelo R y S deben ser groseros y furtivos porque el alelo para grosero (R) es dominante al alelo para respetuoso (r) y el alelo para furtivo (S) es dominante al alelo para sincero (s).

    3. Después de completar el cuadrado Punnet, necesitamos averiguar cuántas de las combinaciones de genotipos de descendencia contienen solo los alelos r y s recesivos porque esa es la única manera de expresar la combinación de fenotipos respetuosa y sincera.

      En general, hay 0 combinaciones de genotipos con solo los alelos r y s recesivos y así, una probabilidad 0/16 de que la descendencia sea respetuosa y sincera.

    4. La respuesta correcta es

      0/16

    Consulta\(\PageIndex{2}\)

    Solución paso a paso

    1. El padre es homocigótico recesivo (bb), por lo que sólo puede dar el alelo b recesivo a la descendencia, mientras que la madre es homocigótica dominante (BB), por lo que sólo puede dar el alelo B dominante a la descendencia. La cruz para estos padres es bb x BB.

    2. Podemos completar un cuadrado Punnett para encontrar los posibles genotipos de crías.

      Cruz: bb x BB

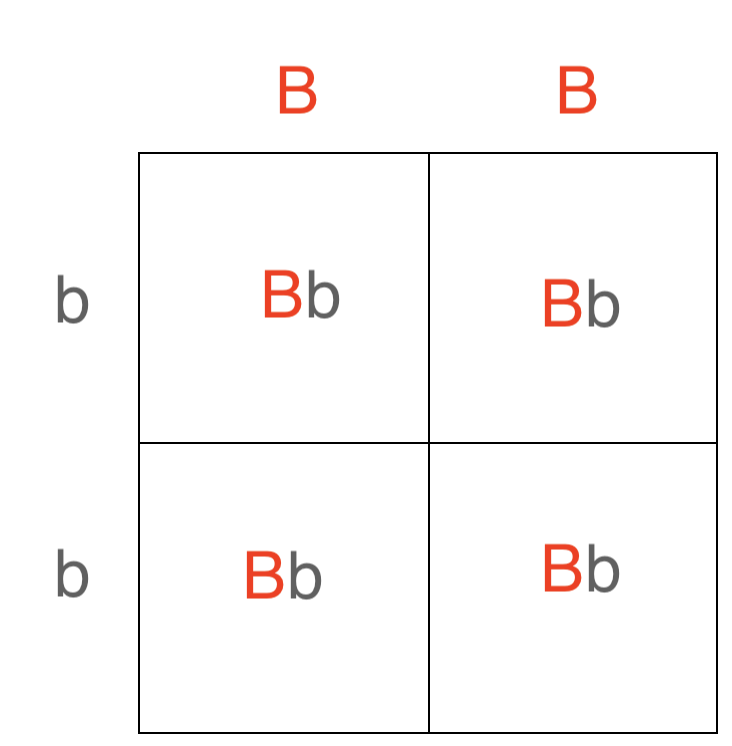
      Conjunto monohíbrido de Punnett cuadrado que muestra proporciones de genotipos de un cruce bb x BB

      Si completamos la cruz, encontramos que la posible descendencia solo puede ser Bb. Las crías que tienen al menos un alelo B deben ser aburridas porque el alelo para aburrido (B) es dominante al alelo para ocupado (b).

    3. Si completamos el cruce, encontramos que hay un 100% de posibilidades de que la descendencia sea Bb (aburrida). No hay otras combinaciones posibles de genotipos.

    4. La respuesta correcta es

      Solo Bb

    Consulta\(\PageIndex{3}\)

    Solución paso a paso

    1. Debido a que aquí hay dos rasgos, debemos realizar un cruce dihíbrido. Conocemos los genotipos progenitores (cCDD y cCDD), pero necesitamos averiguar cuáles son los gametos posibles averiguando todas las combinaciones posibles de los dos alelos.

      Para ambos padres, el genotipo cCDD conduce a las posibles combinaciones de gametos de CD, Cd, cD o cd.

    2. A continuación, realizaremos el cruce dihíbrido.

      Cruz: cCDd x cCDd

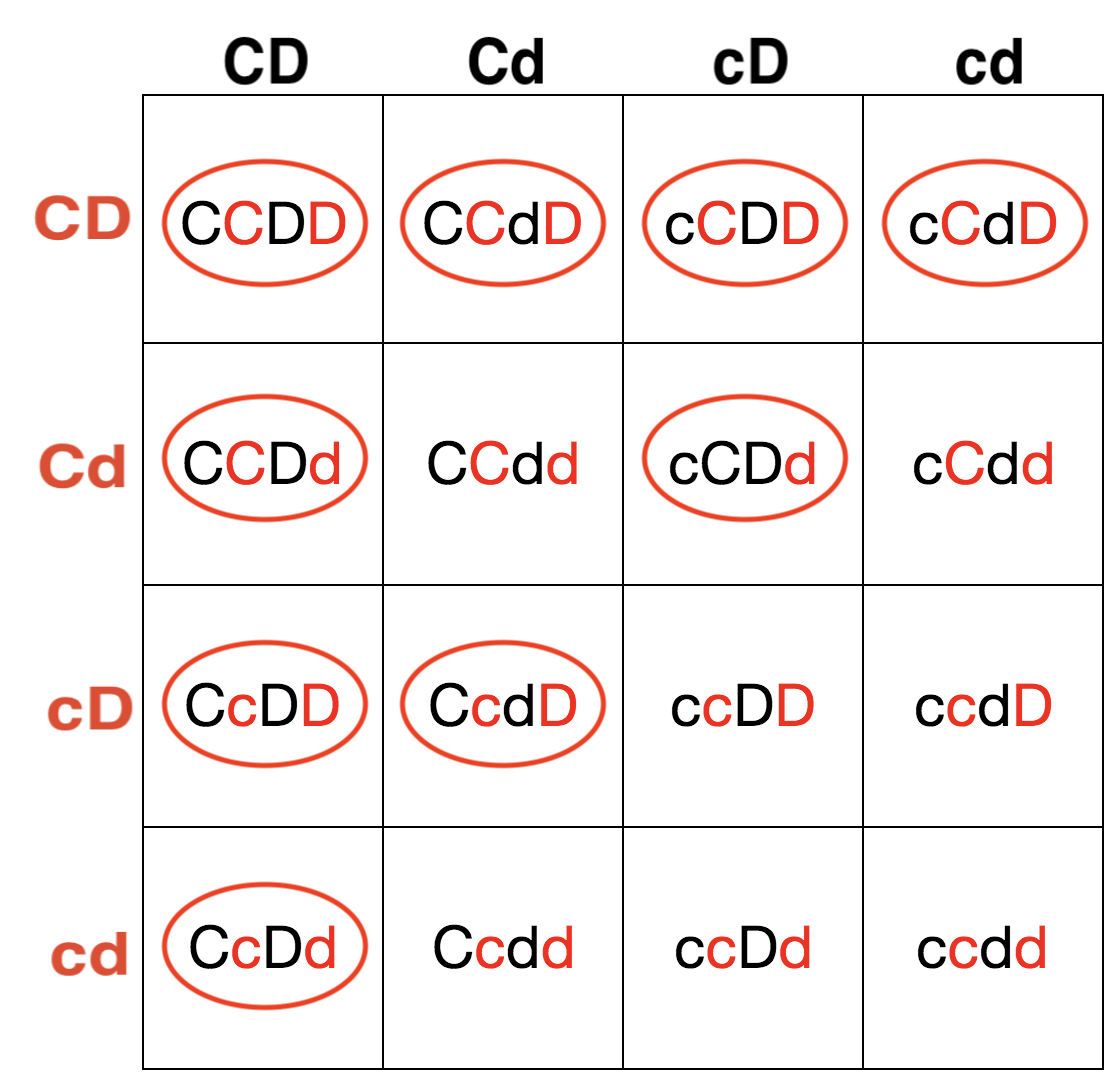
      Configuración cuadrada de Punnett dihíbrida que muestra proporciones de genotipos de un cruce de cCDD x cCDD

      Después de completar el cruce, necesitamos averiguar cuántas de las combinaciones de genotipos de descendencia contienen al menos un alelo C dominante y un alelo D dominante para obtener la torpe y deslumbrante combinación de fenotipos.

    3. Debido a que estamos buscando la proporción de crías que son a la vez torpes y deslumbrantes, podemos referirnos a los genotipos en círculo\({\color{Red} red}\) en la plaza Punnett. Todas estas cajas contienen al menos un alelo C dominante y un alelo D dominante.

      En general, hay 9 genotipos en\({\color{Red} red}\) círculo y, por lo tanto, una probabilidad de 9/16 de que la descendencia sea torpe y deslumbrante.

    4. La respuesta correcta es

      9/16

    Consulta\(\PageIndex{4}\)

    Solución paso a paso

    1. La madre es heterocigota, por lo que posiblemente pueda dar uno de cualquiera de los alelos (P o p) a la descendencia, mientras que el padre es homocigótico dominante (PP), por lo que sólo puede dar el alelo P dominante a la descendencia. La cruz para estos padres es Pp x PP.

    2. Podemos completar un cuadrado Punnett para encontrar los posibles genotipos de crías.

      Cruz: Pp x PP

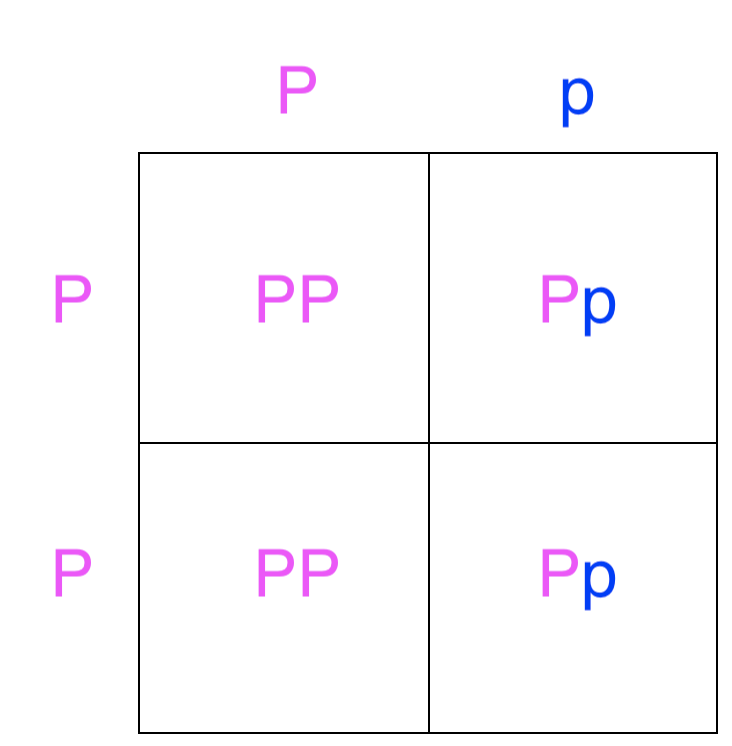
      Cuadrado monohíbrido de Punnett que muestra proporciones de genotipos de un cruce PP x Pp

      Si completamos el cruce, encontramos que la posible descendencia puede ser PP o Pp. Las crías que tienen al menos un alelo P deben ser juguetonas porque el alelo para lúdico (P) es dominante al alelo para paranoide (p).

    3. Si completamos el cruce, encontramos que hay un 50% de probabilidad de que la descendencia sea PP (juguetona) y también un 50% de probabilidad de que la descendencia sea Pp (juguetona). No hay otras combinaciones posibles de genotipos.

    4. La respuesta correcta es

      PP y Pp

    Consulta\(\PageIndex{5}\)

    Solución paso a paso

    1. Debido a que aquí hay dos rasgos, debemos realizar un cruce dihíbrido. Conocemos los genotipos progenitores (Bbhh y BBhh), pero necesitamos averiguar cuáles son los gametos posibles averiguando todas las combinaciones posibles de los dos alelos.

      Para el padre Bbhh, las posibles combinaciones de gametos son Bh, Bh, bh o bh.

      Para el progenitor BBhh, las posibles combinaciones de gametos son bH, bH, bh o bh.

    2. A continuación, realizaremos el cruce dihíbrido.

      Cruz: Bbhh x BBhh

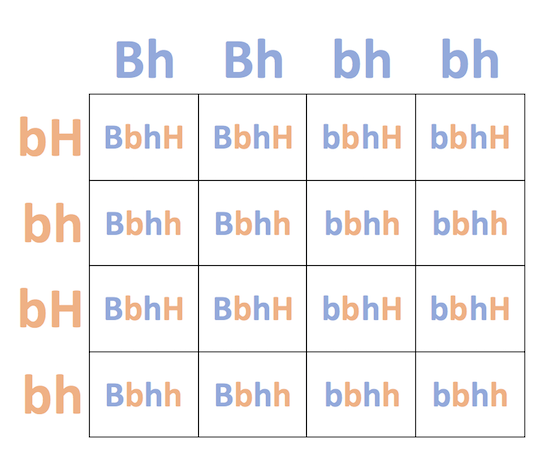
      Configuración de cuadraditos punnett dihíbridos que muestra proporciones de genotipos de un cruce Bbhh x BBhh

      Al completar el cruce, encontramos que los posibles genotipos de crías son bbhh, bbhh, bbhh o bbhh.

    3. Debido a que estamos buscando la proporción de crías que son marrones con pelaje largo, necesitamos identificar crías que son dominantes para el gen del color del pelaje (ya sea BB o Bb), y recesivas para el gen de longitud de pelaje (hh).

      Si nos fijamos en nuestro cuadrado Punnett, el único genotipo que muestra estos fenotipos es Bbhh.

      Existe una probabilidad de 4/16 de que la descendencia sea marrón con pelaje largo, o Bbhh.

      4/16 = 1/4 = 25%

    4. La respuesta correcta es

      25%

    Consulta\(\PageIndex{6}\)

    Solución paso a paso

    1. Cuando esté presente un alelo dominante, se expresará. La madre y el padre tienen cada uno el genotipo Aa, lo que significa que cada uno tendrá peines de guisante debido al alelo A.

      La cruz para estos padres es Aa x Aa.

    2. Podemos completar un cuadrado Punnett para encontrar las posibles combinaciones de crías.

      Cruz: Aa x Aa

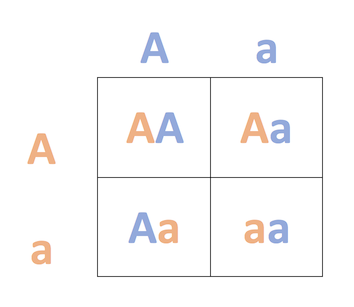
      Configuración monohíbrida de punnett cuadrada que muestra proporciones de genotipos de un cruce de Aa x Aa

      Si completamos el cruce, encontramos que la posible descendencia puede ser AA, Aa o aa. Las crías que tienen un alelo A deben tener peines de guisante, porque el alelo para peines de guisante (A) es dominante al alelo para peines individuales (a). Solo aa crías tendrán peines individuales.

    3. Si miramos nuestra plaza Punnett, encontramos que hay un 1/4 de probabilidad de que la descendencia tenga el genotipo para peines individuales (aa). Si convertimos esto a un porcentaje, significa que hay un 25% de posibilidades de que estos padres tengan descendencia con peines individuales.

    4. La respuesta correcta es

      25%

    Consulta\(\PageIndex{7}\)

    Solución paso a paso

    1. Debido a que aquí hay dos rasgos, debemos realizar un cruce dihíbrido. Conocemos los genotipos progenitores (sStT y SstT), pero necesitamos averiguar cuáles son los gametos posibles averiguando todas las combinaciones posibles de los dos alelos.

      Para ambos padres, el genotipo sStT conduce a las posibles combinaciones de gametos de ST, St, sT o st.

    2. A continuación realizaremos el cruce dihíbrido.

      Cruz: SStT x SStT

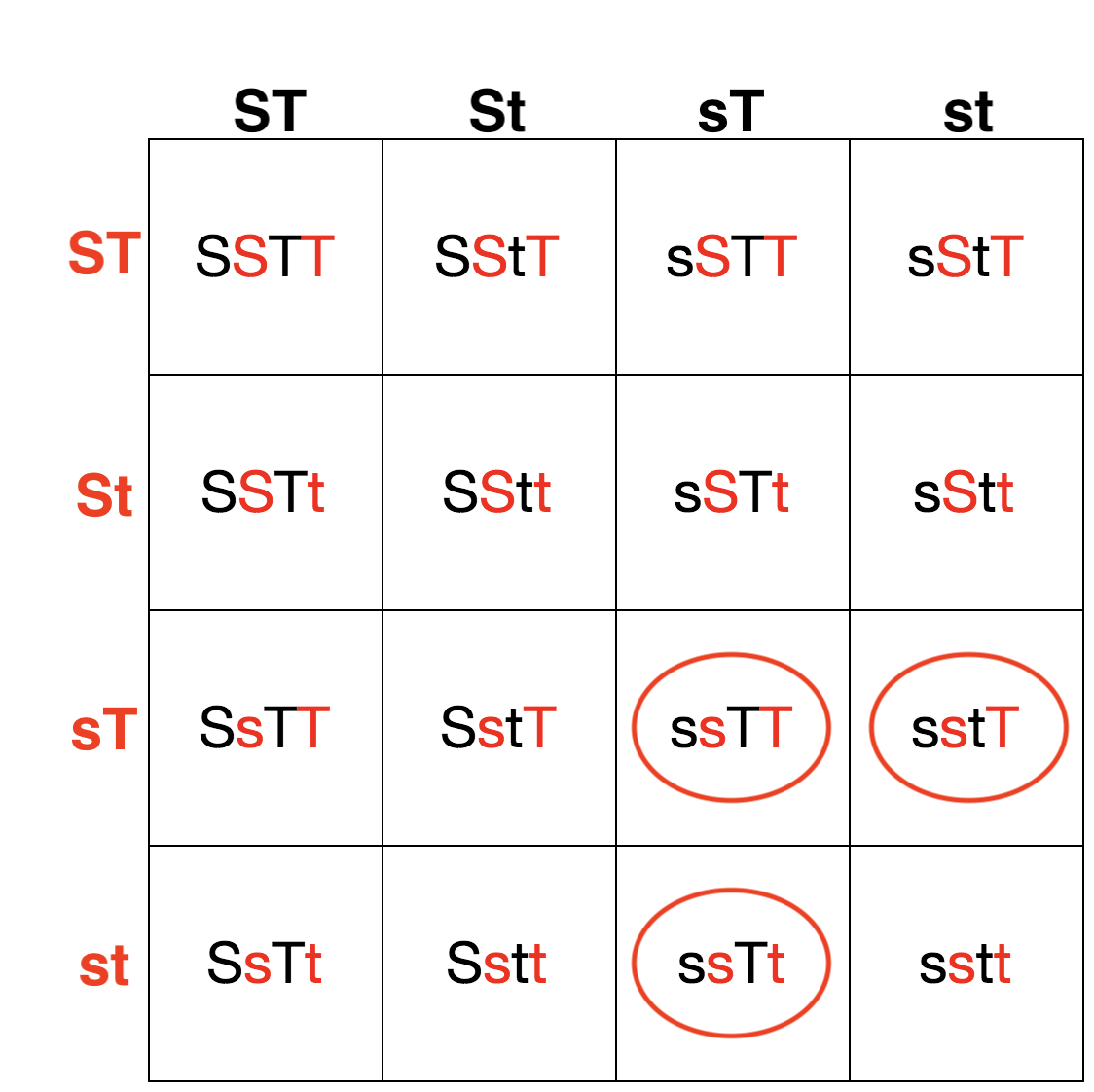
      Configuración cuadrada de Punnett dihíbrida que muestra proporciones de genotipos de un cruce de SstT x SstT

      Después de completar el cruce, necesitamos averiguar cuántas de las combinaciones de genotipos de descendencia contienen dos alelos recesivos y al menos un alelo T dominante para obtener la combinación de fenotipos atrevida y oportuna.

    3. Debido a que estamos buscando la proporción de crías que sean a la vez descaradas y oportunas, podemos referirnos a los genotipos en círculo\({\color{Red} red}\) en la plaza Punnett. Todas estas cajas contienen dos alelos s recesivos y al menos un alelo T dominante.

      En general, hay 3 genotipos en\({\color{Red} red}\) círculo y, por lo tanto, una probabilidad de 3/16 de que la descendencia sea atrevida y oportuna. Cuando se convierte a un porcentaje, 3/16 = 18.75%.

    4. La respuesta correcta es

    Consulta\(\PageIndex{8}\)

    Solución paso a paso

    1. Cuando esté presente un alelo dominante, se expresará. Ambos progenitores son heterocigotos (Kk), lo que significa que cada uno tendrá granos lisos debido al alelo K.

      La cruz para estos padres es Kk x Kk.

    2. Podemos completar un cuadrado Punnett para encontrar las posibles combinaciones de crías.

      Cruz: Kk x Kk

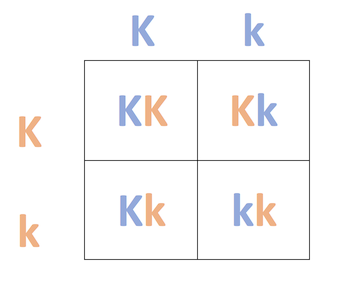
      Conjunto monohíbrido de punnett cuadrado que muestra proporciones de genotipos de un cruce de Kk x Kk

      Si completamos la cruz, encontramos que la posible descendencia puede ser KK, Kk o kk. Las crías que tienen un alelo K deben tener granos lisos porque el alelo para granos lisos (K) es dominante al alelo para granos arrugados (k). Solo las crías kk tendrán granos arrugados.

    3. Si miramos nuestro cuadrado Punnett, encontramos que existe una probabilidad de 1/4 de que la descendencia sea homocigótica dominante para los granos lisos (KK) y una probabilidad de 2/4 de que la descendencia sea heterocigota (Kk) para los granos lisos.

      Combinados, encontramos que hay una probabilidad de 3/4 de que la descendencia tenga granos lisos.

    4. La respuesta correcta es

      3/4

    Consulta\(\PageIndex{9}\)

    Solución paso a paso

    1. Debido a que aquí hay dos rasgos, debemos realizar un cruce dihíbrido. Conocemos los genotipos progenitores (aABb y aabb), pero necesitamos averiguar cuáles son los gametos posibles averiguando todas las combinaciones posibles de los dos alelos.

      Para el progenitor AAbB, las posibles combinaciones de gametos son AB, AB, Ab o Ab.

      Para el progenitor aabb, las posibles combinaciones de gametos son ab, ab, ab o ab.

    2. A continuación, realizaremos el cruce dihíbrido.

      Cruz: AAbB x aabb

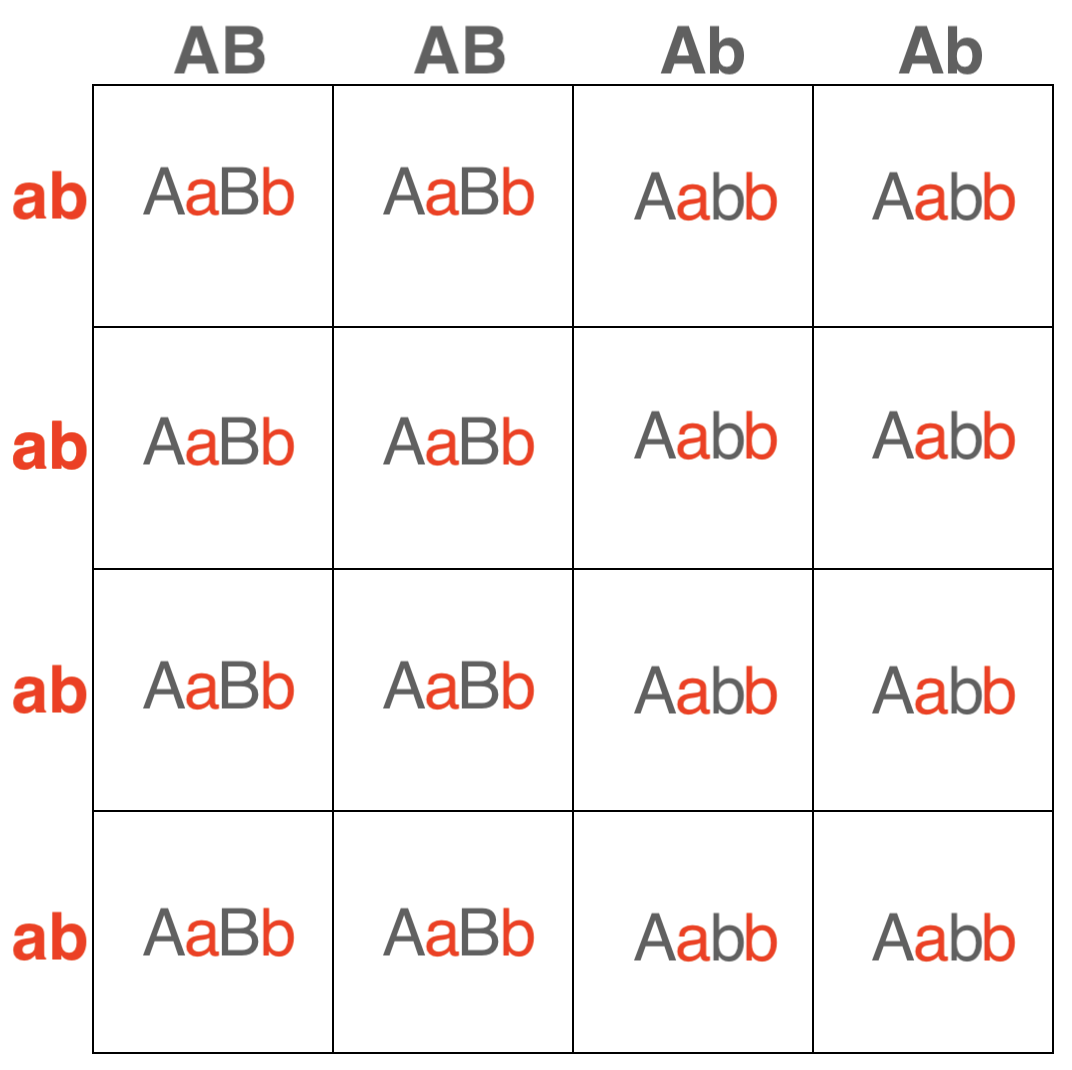
      Configuración cuadrada de Punnett dihíbrida que muestra proporciones de genotipos de un cruce de aABb x aabb

      Al completar el cruce, encontramos que los posibles genotipos de descendencia son AAbB o Aabb.

    3. Debido a que estamos buscando la proporción de crías que son heterocigóticas para ambos rasgos, necesitamos identificar crías que sean heterocigóticas para el rasgo impresionante (Aa) y heterocigóticas para el rasgo tímida (Bb).

      Si nos fijamos en nuestro cuadrado Punnett, el único genotipo dihíbrido que es heterocigoto para ambos rasgos es aAbB.

      Existe una probabilidad de 8/16 de que la descendencia sea impresionante y tímida, o heterocigótica para ambos rasgos con el genotipo AaBb.

      8/16 = 1/2 = 50%

    4. La respuesta correcta es

      50%

    Consulta\(\PageIndex{10}\)

    Solución paso a paso

    1. El caballo negro homocigótico tiene un genotipo de BB. Homocigótico significa que tiene dos de los mismos alelos, y es negro, por lo que el alelo es B.

      El castaño de caballo tiene un genotipo de bb porque solo puede ser castaño si tiene dos alelos recesivos (b). Si tuviera hasta un alelo B, sería negro.

      La cruz para estos padres es BB x bb.

    2. Podemos completar un cuadrado Punnett para encontrar las posibles combinaciones de crías.

      Cruz: BB x bb

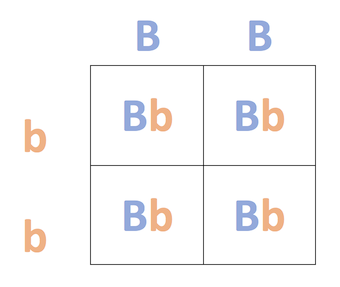
      Configuración monohíbrida de punnett cuadrada que muestra proporciones de genotipos de un cruce BB x bb

      Si completamos la cruz, encontramos que la única descendencia posible solo puede ser Bb. Las crías que tienen un alelo B deben ser negras porque el alelo para el color negro (B) es dominante al alelo para el color castaño (b). Por lo que toda la descendencia producida será negra.

    3. Si miramos nuestra plaza Punnett, encontramos que existe una probabilidad 0/4 de que la descendencia sea castaña porque la descendencia Bb mostrará el rasgo dominante (negro). Si convertimos esto a un porcentaje, significa que hay un 0% de probabilidad de que estos padres tengan descendencia castaña.

    4. La respuesta correcta es

      0%

    Consulta\(\PageIndex{11}\)

    Solución paso a paso

    1. Debido a que aquí hay dos rasgos, debemos realizar un cruce dihíbrido. Conocemos los genotipos progenitores (Ttgg y TTGG), pero necesitamos averiguar cuáles son los gametos posibles averiguando todas las combinaciones posibles de los dos alelos.

      Para el progenitor Ttgg, las posibles combinaciones de gametos son Tg, Tg, tg o tg.

      Para el progenitor tGG, las posibles combinaciones de gametos son tG, tG, tg o tg.

    2. A continuación, realizaremos el cruce dihíbrido.

      Cruz: Ttgg x TTgg

      Configuración cuadrado-punnett dihíbrida que muestra proporciones de genotipos de un cruce Ttgg x tTGG

      Al completar el cruce, encontramos que las posibles crías son tGG, tTGG, Ttgg o ttgg.

    3. Debido a que estamos buscando la proporción de crías que son cortas con guisantes amarillos, sabemos que estamos buscando una descendencia completamente recesiva, o descendencia con genotipo ttgg.

      Si miramos nuestra plaza Punnett, encontramos que existe una probabilidad de 4/16 de que la descendencia sea corta con guisantes amarillos, o ttgg. Entonces podemos reducir esta oportunidad a 1/4.

    4. La respuesta correcta es

      1/4

    Consulta\(\PageIndex{12}\)

    Solución paso a paso

    1. La madre y el padre son heterocigotos, por lo que ambos posiblemente puedan dar uno de cualquiera de los alelos (S o s) a la descendencia. La cruz para estos padres es Ss x Ss.

    2. Podemos completar un cuadrado Punnett para encontrar los posibles genotipos de crías.

      Cruz: Ss x Ss

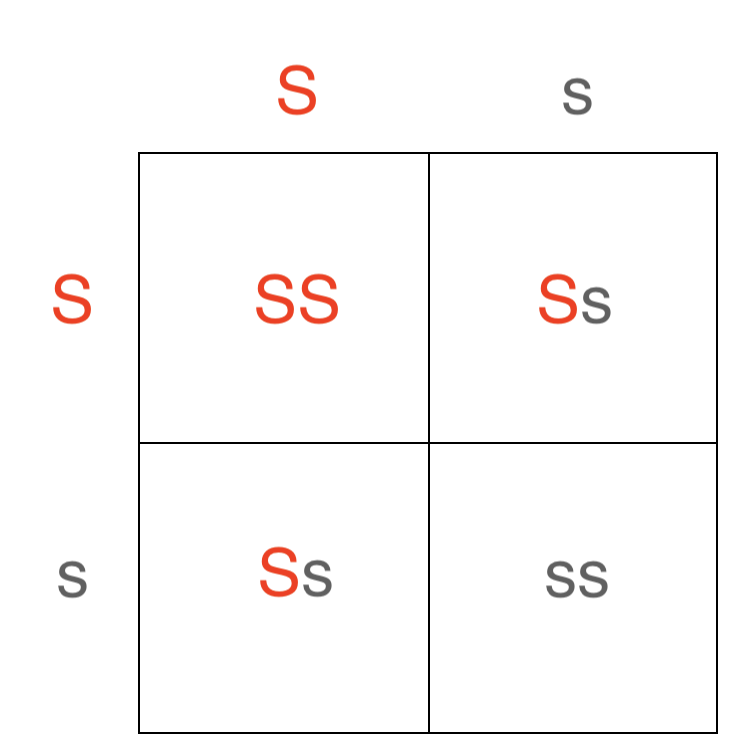
      Configuración de cuadrados Punnett monohíbridos que muestran proporciones de genotipos de un cruce de Ss x Ss

      Si completamos la cruz, encontramos que la posible descendencia puede ser SS, Ss, o ss. Las crías que tienen al menos un alelo S dominante deben estar sanas (sin anemia falciforme) porque el alelo para sano (S) es dominante al alelo para anemia de células falciformes. Solo las crías ss tendrán anemia falciforme.

    3. Si completamos el cruce, encontramos que existen 2/4 posibles genotipos de crías que son heterocigotos (Ss). Entonces podemos reducir esta oportunidad a 1/2.

    4. La respuesta correcta es

      1/2

    Colaboradores y Atribuciones

    1.10: Práctica - Cuadrados de Punnett y probabilidad is shared under a CC BY-NC-SA 3.0 license and was authored, remixed, and/or curated by LibreTexts.