5.2.2: Estimación del número de células
- Page ID
- 51445
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Recuento total de células al microscopio
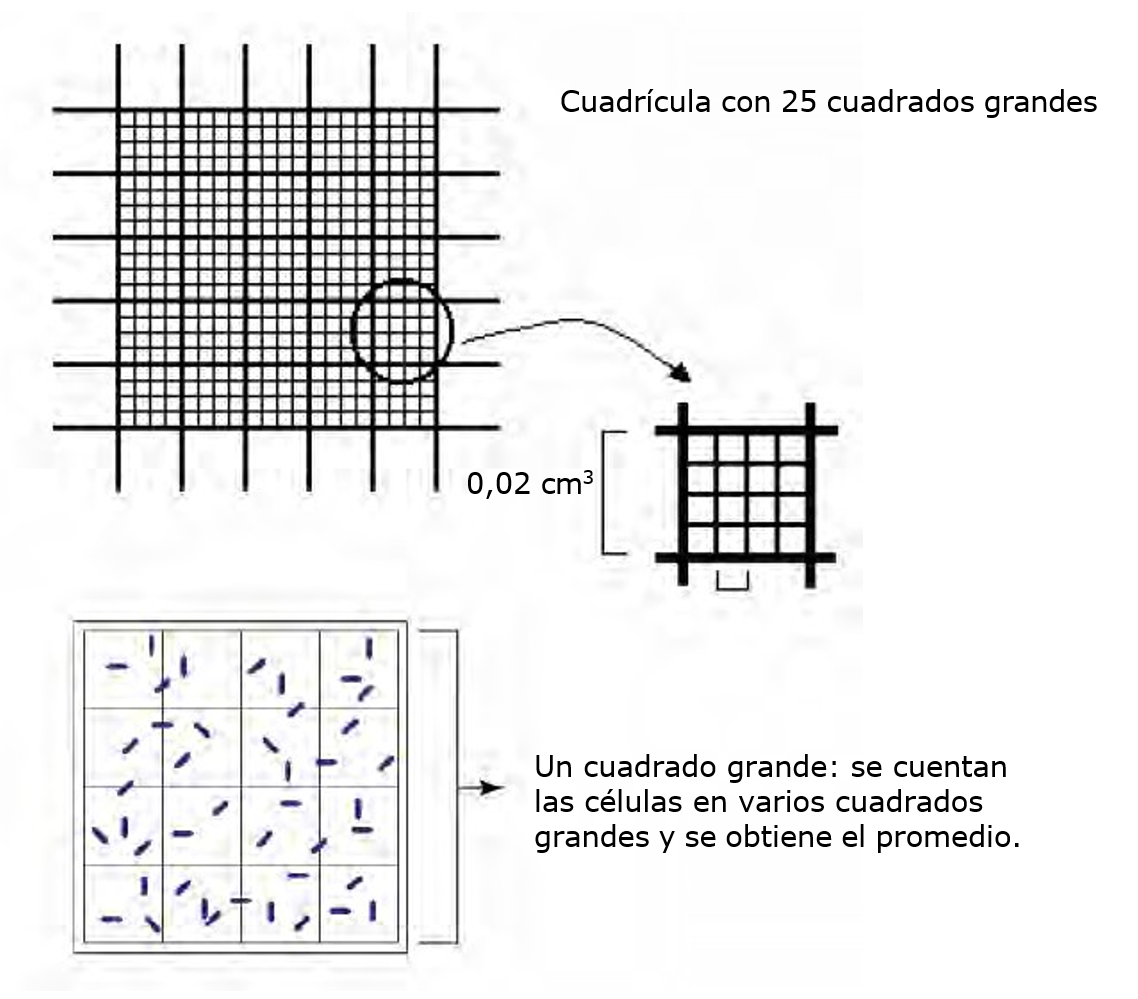
Fundamento: se requiere de cámaras especiales de contaje, tales como la de Petroff-Hausser (Figura 5.2). La cámara consta de 25 cuadrados grandes (cada uno dividido en 16 cuadrados más pequeños) con un área total de 1 mm2 y una profundidad de 0,02 mm.
La muestra se coloca en la cámara, entre el portaobjetos y el cubreobjetos, se deja reposar sobre la plataforma del microscopio durante unos minutos, y se cuenta el número de células en varias celdillas o cuadrados (por lo menos en 5) y se calcula la media (por ejemplo 12 células).
Para calcular el número de células por mililitro de muestra:
\[ 12 \text{ celas } \times 25 \text{ cuadrados } \times 50 \text{ factor del volumen de la cámara } \times 10^{3} = 1.7 \times 10^{7} \text{ células/ml } \]
Ventajas: es un método muy rápido, sencillo y económico.
Desventajas: sólo sirve para suspensiones relativamente concentradas (>106 cél/ml). Por debajo de este valor el número de células vistas en el campo del microscopio es muy pequeño previamente, con una mezcla de alcohol y agua.
Utilidad: este método es aplicable a organismos unicelulares (levaduras y bacterias) y esporas fúngicas.
Método del número más probable (NMP)
Fundamento: este método se fundamenta en el presupuesto de que en una serie de diluciones de la muestra sembradas en tubos con medio líquido, para que se observe desarrollo en el tubo debe por lo menos haber una célula en el inóculo sembrado. Con esta consigna y aplicando análisis probabilístico según las diluciones y cantidades de tubos de la serie usada (triplicado, quintuplicado u otras variantes) se construyen tablas del NMP/100 ml de muestra, que se puede calcular con un 95% de confianza para cada una de las situaciones numéricas de la serie usada (Tabla \(\PageIndex{1}\)).
Por ejemplo, una serie muy usada en el análisis de aguas es la serie de tres diluciones por triplicado, en ella se siembran 3 tubos de 10 ml de muestra, seguido de 3 de 1 ml y 3 de 0,1 ml. Luego de la incubación se observa el crecimiento en los tubos buscando el límite de crecimiento (el primer tubo sin desarrollo de la serie) y a partir de él se establece el número indicativo de la serie para buscar su equivalente en NMP/100 en la tabla correspondiente.
Supongamos que el número de tubos positivos por serie de tres resultan 3, 1, 0 respectivamente; esta combinación en la tabla nos indica un NMP de 43/100. Desde el punto de vista estadístico esto significa que el 95% de las muestras de agua que dan este resultado contienen entre 7 y 210 bacterias y el número más probable es 43.
Tabla \(\PageIndex{1}\). Índice del NMP y límites de confianza 95% para varias combinaciones de resultados positivos y negativos cuando se utilizan tres alícuotas de 10 ml, 3 de 1 ml y tres de 0,1 ml.
|
Número de tubos positivos del total de |
Índice del NMP por 100 ml |
Límites de confianza |
|||
|---|---|---|---|---|---|
|
3 tubos de 10 ml |
3 tubos de 1 ml |
3 tubos de 0,1 ml |
Inferior |
Superior |
|
|
0 |
0 |
1 |
3 |
0,5 |
9 |
|
0 |
1 |
0 |
3 |
0,5 |
13 |
|
1 |
0 |
0 |
4 |
0,5 |
20 |
|
1 |
0 |
1 |
7 |
1 |
21 |
|
1 |
1 |
0 |
7 |
1 |
23 |
|
1 |
1 |
1 |
11 |
3 |
36 |
|
1 |
2 |
0 |
11 |
3 |
36 |
|
2 |
0 |
0 |
9 |
1 |
36 |
|
2 |
0 |
1 |
14 |
3 |
37 |
|
2 |
1 |
0 |
15 |
3 |
44 |
|
2 |
1 |
1 |
20 |
7 |
89 |
|
2 |
2 |
0 |
21 |
4 |
47 |
|
2 |
2 |
1 |
28 |
10 |
150 |
|
2 |
0 |
0 |
23 |
4 |
120 |
|
3 |
0 |
1 |
39 |
7 |
130 |
|
3 |
0 |
2 |
64 |
15 |
380 |
|
3 |
1 |
0 |
43 |
7 |
210 |
|
3 |
1 |
1 |
75 |
14 |
230 |
|
3 |
1 |
2 |
120 |
30 |
380 |
|
3 |
2 |
0 |
93 |
15 |
380 |
|
3 |
2 |
1 |
150 |
30 |
440 |
|
3 |
2 |
2 |
210 |
35 |
470 |
|
3 |
3 |
0 |
240 |
36 |
1300 |
|
3 |
3 |
1 |
460 |
71 |
2400 |
|
3 |
3 |
2 |
1100 |
150 |
4800 |
Recuento de viables en placa
Fundamento: permite la determinación de los microorganismos presentes en una muestra en base a su desarrollo en medio de cultivo en placas, formando colonias. Por lo tanto, se determinan por este método sólo las células microbianas viables en las condiciones de trabajo elegidas (nutrientes, atmósfera, temperatura) (Figura 5.3). Una ventaja importante de esta técnica es que mide el número de células viables. Una desventaja es que se requiere bastante tiempo, por lo general 24 h o más, para que se formen las colonias viables.
Utilidad: este método es aplicable a organismos unicelulares (levaduras y bacterias) y hongos filamentosos.
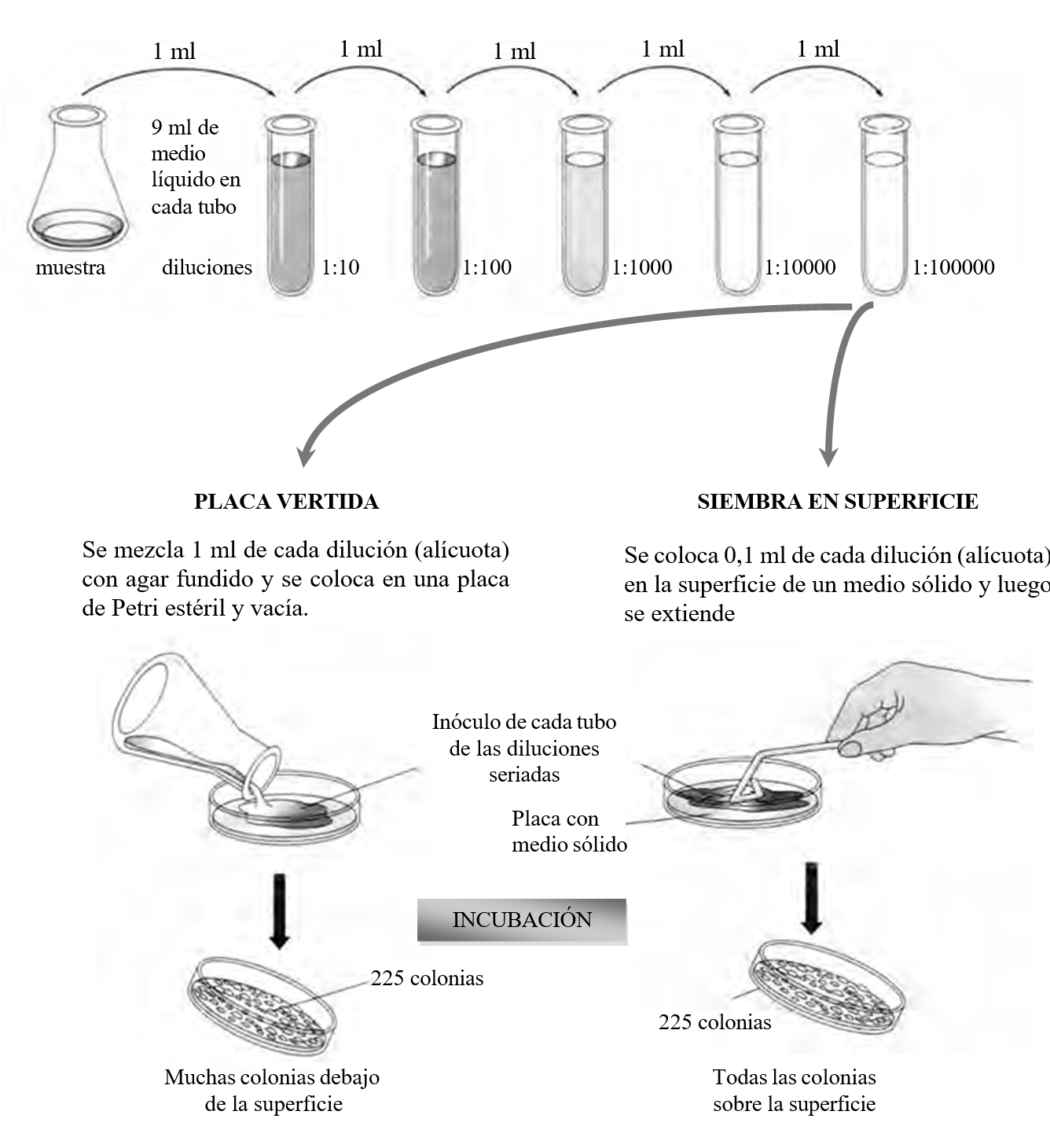
Para calcular el número de unidades formadoras de colonias por mililitro o gramo de muestra (UFC/g o UFC/ml), se procede de la siguiente manera:
Siembra en superficie:
\[\begin{matrix}
\text{Promedio del número de colonias} & \times & \text{factor de dilución} & \times & \text{factos de alícuota} & = \text{UFC/g o UFC/ml} \\
225 & \times & 10^{5} & \times & 10 & = & 2,25 x 10^{8} \text{ufc/ml}
\end{matrix}
\]
Siembra en profundidad:
\[\begin{matrix}
\text{Promedio del número de colonias} & \times & \text{factor de dilución} & \times & \text{factos de alícuota} & = \text{UFC/g o UFC/ml} \\
225 & \times & 10^{5} & \times & 1 & = & 2,25 x 10^{8} \text{ufc/ml}
\end{matrix}
\]
Determinación de la proporción células viables/células totales
Si se está interesado en conocer esa proporción se recurre a una técnica de microcultivos en cubreobjetos, hay que seguir periódicamente la evolución del crecimiento de células individuales y determinar la proporción de aquellas células no viables (visibles al microscopio, pero incapaces de crecer).
Recuento sobre filtros de nitrocelulosa
Se usa para suspensiones diluidas de bacterias. Se hace pasar un gran volumen de suspensión a través de una membrana de nitrocelulosa estéril, que retiene las bacterias. Posteriormente, el filtro se deposita sobre la superficie de un medio de cultivo sólido. Las colonias se forman sobre el filtro y se cuentan, deduciéndose la concentración original en función del volumen de suspensión que se hizo pasar por el filtro.
Otros métodos
Recuento en preparaciones teñidas, recuento proporcional de Wright, contadores electrónicos de partículas (tipo Coulter), etc.


