3.4: Problemas
- Page ID
- 81935
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\ket}[1]{\left| #1 \right>}\)
\(\newcommand{\bra}[1]{\left< #1 \right|}\)
\(\newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>}\)
\(\newcommand{\braopket}[3]{\left< #1 \vphantom{#2}\vphantom{#3} \right| #2 \vphantom{#1}\vphantom{#3} \left| #3 \vphantom{#1}\vphantom{#2} \right>}\)
\(\newcommand{\qmvec}[1]{\mathbf{\vec{#1}}}\)
\(\newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
\(\newcommand{\expect}[1]{\langle #1 \rangle}\)
\(\newcommand{\dfn}[1]{\emph{\textbf{#1}}}\)
3.1. Para cada uno de los tres materiales cristalinos a continuación
- Encuentra el grupo de puntos de cristal al que pertenece. (Pista: use http://www.mindat.org)
- Utilizando la Tabla 2.3.1, determinar si el material es piezoeléctrico o no.
- Utilizando la Tabla 2.3.1, determinar si el material es piroeléctrico o no.
- Utilizando la Tabla 2.3.1, determinar si el material es electroóptico Pockels o no.
a) ZnS (esfalerita)
b) HG (cinabrio)
c) Diamante
3.2. El azúcar de caña, también llamado sacarosa, tiene composición química C\(_12\) H\(_22\) O\(_11\) y pertenece al grupo de puntos cristalinos dado por 2 en notación Hermann-Maguin [38]. La referencia [38] enumera los valores especificados en unidades cgse para su constante piezoeléctrica as\(10.2 \cdot 10^{-8} \frac{\text{esu}}{\text{dyne}}\) y su coeficiente piroeléctrico como\(0.53 \frac{\text{esu}}{cm^2 \cdot ^{\circ}\text{C}}\). Convertir estos valores a las unidades SI de\(\frac{m}{V}\) y\(\frac{C}{m^2\cdot K}\) respectivamente.
Pista: La unidad electrostática o statculomb es una medida de carga [7] donde\[ 1 \text{ esu} = 1 \text{ statC} = 3.335641 \cdot 10^{-10} C \nonumber \] y la dina es una medida de fuerza donde\( 1 \text{ dyne} = 10^{-5} N \).
3.3. Un material tiene permitividad relativa\(\epsilon_{r\;x}\) cuando no se aplica campo eléctrico externo. El coeficiente\(\chi^{(2)}\) se mide en presencia de un campo eléctrico externo de intensidad\(|\overrightarrow{E}|\). Supongamos que\(\chi^{(3)}\) y todos los coeficientes de orden superior son cero. Encuentre el coeficiente\(\gamma\) de Pockels en función de las cantidades conocidas\(\epsilon_{r\;x}\),\(\chi^{(2)}\), y\(|\overrightarrow{E}|\).
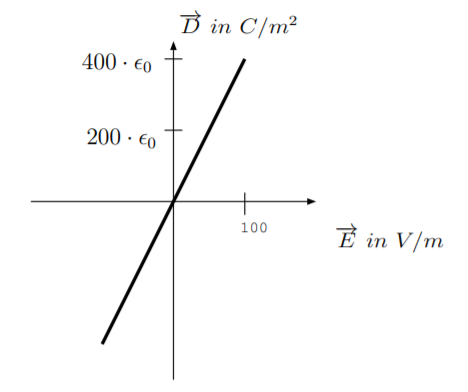
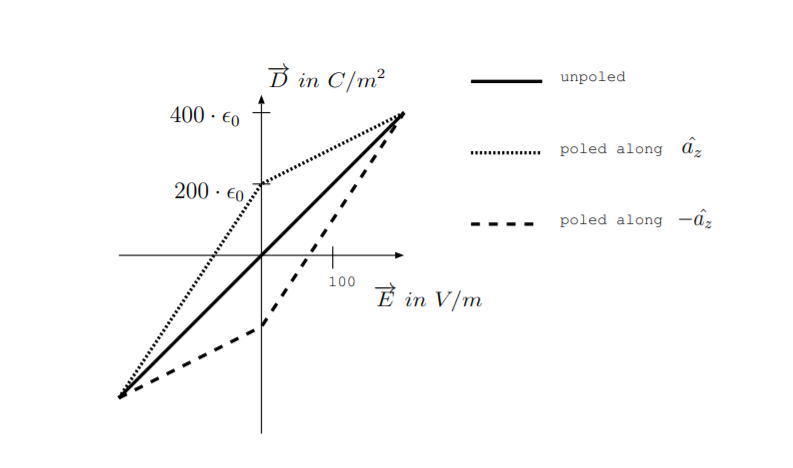
3.4. La primera figura a continuación muestra la densidad\(|\overrightarrow{D}|\) de flujo de desplazamiento en función de la intensidad de una intensidad de campo eléctrico aplicada\(|\overrightarrow{E}|\) en un material no electro-óptico. La segunda figura a continuación muestra la densidad\(|\overrightarrow{D}|\) de flujo de desplazamiento en función de la intensidad de una intensidad de campo eléctrico aplicada\(|\overrightarrow{E}|\) en un material electroóptico ferroeléctrico. La línea continua corresponde a un material no polarizado. La línea punteada corresponde al material después de haber sido polarizado en la\(\hat{a}_z\) dirección, y la línea discontinua corresponde al material después de haber sido polarizado en la\(-\hat{a}_z\) dirección.
(a) Para el material no electro-óptico, encontrar la permitividad relativa,\(\epsilon_r\). También encontramos la magnitud de la polarización material,\(\overrightarrow{P}\).
(b) Supongamos que el material electroóptico ferroeléctrico es polarizado por un campo eléctrico externo fuerte, y luego se elimina el campo. Encuentra la magnitud de la polarización del material\(|\overrightarrow{P}|\) después de eliminar el campo externo.
(c) Supongamos que el material ferroeléctrico es polarizado en la\(-\hat{a}_z\) dirección por un campo externo fuerte, y luego se elimina el campo. Se aplica un campo eléctrico externo diferente dado por\(\overrightarrow{E} = 100\hat{a}_z \frac{V}{m}\). Encuentra la permitividad relativa aproximada del material.
3.5. Un material cristalino es tanto piezoeléctrico como piroeléctrico. Cuando se aplica un campo eléctrico externo de,\(|\overrightarrow{E}| = 100 \frac{V}{m}\) se determina que la polarización del material es\(|\overrightarrow{P}| = 1500\epsilon_0 \frac{C}{m^2}\). Cuando se aplican tanto una tensión de\(|\overrightarrow{\varsigma}| = 30 \frac{N}{m^2}\) como un campo eléctrico externo de,\(|\overrightarrow{E}| = 100 \frac{V}{m}\) se determina que la polarización del material es\(|\overrightarrow{P}| = 6.0123 \cdot 10^{-6} \frac{C}{m^2}\). Cuando se aplica un gradiente de temperatura de\(\Delta T = 50\; ^\circ C\)\(|\overrightarrow{\varsigma}| = 30 \frac{N}{m^2}\), una tensión de, y un campo eléctrico externo de,\(|\overrightarrow{E}| = 100 \frac{V}{m}\) se determina que la polarización del material es\(|\overrightarrow{P}| = 6.3 \cdot 10^{-6} \frac{C}{m^2}\). Encuentra:
- La permitividad relativa del material
- La constante de deformación piezoeléctrica
- La magnitud del coeficiente piroeléctrico