3.1: Solución Inicial

Lo que sabes hasta ahora:

1. La restricción presupuestal muestra los posibles paquetes de consumo del consumidor. La restricción lineal estándar es\(p_1x_1 + p_2x_2 = m\). Hay muchas otras situaciones, como los subsidios y el racionamiento, que dan restricciones más complicadas con torceduras y segmentos horizontales/verticales.

2. El mapa de indiferencia muestra las preferencias del consumidor. La situación estándar es un conjunto de curvas de indiferencia convexas, inclinadas hacia abajo. Hay muchas preferencias alternativas, como sustitutos perfectos y complementos perfectos. Las preferencias son capturadas por las funciones de utilidad, que reflejan con precisión la forma de las curvas de indiferencia.

Nuestro trabajo es combinar estas dos partes, una expresando lo que es asequible y la otra lo deseable, para encontrar la combinación (o paquete) que maximice la satisfacción (como se describe en el mapa de indiferencia o función de utilidad) dada la restricción presupuestal. La respuesta será en cuanto a cuánto comprará el consumidor en unidades de cada bien.

La solución óptima se representa mediante la gráfica canónica en la Figura 3.1. La palabra canónica se usa aquí para significar estándar, convencional u ortodoxo. En economía, una gráfica canónica es una gráfica central, esencial que es entendida por todos los economistas, como una gráfica de oferta y demanda.

No es exagerado decir que la Figura 3.1 es una de las gráficas más fundamentales e importantes en economía. Es la base de la Teoría del Comportamiento del Consumidor y con ella derivaremos una curva de demanda.

Figura 3.1: La gráfica canónica de la solución óptima.

Un serio obstáculo intelectual con la Figura 3.1 es que es altamente abstracta. A continuación se trabaja en un problema concreto, con números reales, para explicar lo que está pasando en esta gráfica fundamental.

Antes de sumergirnos, necesitamos discutir estrategias de solución. Hay dos formas de encontrar la solución óptima:

1. Métodos analíticos utilizando álgebra y cálculoeste es el enfoque convencional, papel y lápiz que se ha utilizado desde hace mucho tiempo.

2. Métodos numéricos que utilizan una computadora, por ejemplo, Solverthis de Excel es una estrategia de solución moderna que utiliza la computadora para hacer la mayor parte del trabajo.

Enfoque Analítico

Desafortunadamente, los problemas de optimización restringidos son más difíciles de resolver que los problemas sin restricciones. El apéndice de este capítulo ofrece una breve revisión del cálculo junto con algunas reglas comunes de álgebra y derivadas. Si el material de abajo tiene poco sentido, vaya al apéndice y luego regrese aquí.

Debido a que se trata de un problema de optimización restringido, el enfoque analítico utiliza el método desarrollado por Joseph Louis Lagrange. Su brillante idea se basa en transformar un problema de optimización restringido en un problema sin restricciones y luego resolverlo usando técnicas de cálculo estándar. En el proceso se crea una nueva variable endógena. Puede tener una interpretación económica significativa.

Lagrange nos dio una receta a seguir que requiere cuatro pasos:

1. Reescribe la restricción para que sea igual a cero.

2. Formar la función lagrangea.

3. Tomar derivados parciales con respecto a\(x_1\),\(x_2\), y\(\lambda\).

4. Establezca las derivadas iguales a cero y resuelva para\(x_1\mbox{*}\),\(x_2\mbox{*}\), y\(\lambda\mbox{*}\).

Un ejemplo concreto

Supongamos que un consumidor tiene una función de utilidad Cobb-Douglas con exponentes iguales a 1 y una restricción presupuestal,\(2x_1 + 3x_2 = 100\) (lo que significa que el precio del bien 1 es de $2/unidad, el precio del bien 2 es de $3 por unidad, y el ingreso es de $100).

El problema es maximizar la utilidad sujeta a (s.t.) la restricción presupuestal. Está escrito en forma de ecuación así:\[\max\limits_{x_1,x_2}U(x_1,x_2)=x_1x_2 \\ \textrm{s.t. } 100 = 2x_1 + 3x_2 \nonumber \]

Este problema no se resuelve directamente. Primero se transforma en un problema sin restricciones, y luego se resuelve este problema sin restricciones. Así es como aplicamos la receta desarrollada por Lagrange.

1. Reescribe la restricción para que sea igual a cero.

\(0 = 100 - 2x_1 - 3x_2\)

2. Formar la función lagrangea.

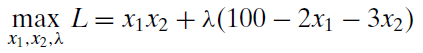
La mayoría de los libros de matemáticas usan un guión elegante L para el Lagrangean\(\mathcal{L}\), así, pero esto es difícil de hacer en el Editor de Ecuaciones de Word (que usarás) por lo que una L extra grande funcionará igual de bien. Además, muchos libros deletrean lagrangean con un i, lagrangiano, pero ambas ortografías son aceptables.

Tenga en cuenta que la función lagrangea, L, está compuesta por la función objetivo original (en este caso, la función de utilidad) más una nueva variable, la letra griega lambda,\(\lambda\), multiplicada por la restricción reescrita. Llamado multiplicador lagrangeo,\(\lambda\) es una nueva variable endógena que se introduce como parte de la estrategia de solución de Lagrange.

El siguiente paso en la receta de Lagrange puede ser intimidante. Este no es el momento de apresurarse y pasar la página. Consulte el apéndice al final de esta sección si las cosas empiezan a ponerse confusas.

3. Tomar derivados parciales con respecto a\(x_1\),\(x_2\), y\(\lambda\).

La derivada utilizada aquí es una derivada parcial, denotada por\(\partial\), que es una forma alternativa de escribir una letra griega minúscula d (razón por la cual también\(\delta\) se usa el símbolo más común para la letra). El símbolo derivado parcial se suele leer como la letra d, por lo que la primera ecuación leída en voz alta sería “d L d x uno es igual a x dos menos dos veces lambda”. También es común leer la derivada en la primera ecuación como “L parcial parcial x uno”.

La derivada parcial es una extensión natural de la derivada regular. Considera la función\(y = 4x^2\). La derivada de y con respecto a x es\(\frac{dy}{dx} = 8x\). Supongamos, sin embargo, que teníamos una función más complicada, así:\(y = 4zx^2\). Esta función multivariante dice que y depende de dos variables, z y x. Podemos explorar la tasa de cambio de esta función a lo largo del eje x tratándola como una función parcial, lo que significa que mantenemos constante la variable z. Entonces la derivada parcial de y con respecto a x es\(\partial y/ \partial x = 8zx\). Si mantenemos x constante y variamos z, entonces la derivada parcial de y con respecto a z es\(\partial y/ \partial z = 4x^2\).

Aplicando esta lógica al Lagrangean en el paso 2, cuando tomamos la derivada parcial con respecto a\(x_1\), el primer término es\(x_2\) porque es como si tuviéramos "x 4" y tomáramos la derivada con respecto a x, obteniendo 4.

Si multiplicamos\(\lambda\) a través de la expresión entre paréntesis en el Lagrangean, obtenemos:\[\lambda (100 - 2x_1 - 3x_2)\\ \lambda 100 - \lambda 2x_1 - \lambda 3x_2 = 0\] Los términos primero y tercero en el lado izquierdo no tienen\(x_1\) por lo que la derivada con respecto a\(x_1\) es cero (al igual que la derivada de una constante es cero). La derivada con respecto al\(x_1\) término medio produce la\(- \lambda 2\) cual se escribe por convención como\(- 2 \lambda\).

¿Se pueden hacer las otras dos derivadas en el paso 3?

4. Establezca las derivadas iguales a cero y resuelva para\(x_1\mbox{*}\),\(x_2\mbox{*}\), y\(\lambda\mbox{*}\).

Existen muchas formas de resolver este sistema de ecuaciones, las cuales se conocen como las condiciones de primer orden. A veces, esta es la parte más difícil del método lagrangeo. Dependiendo de la función de utilidad y restricción, puede que no haya una solución analítica.

Una estrategia común consiste en mover los\(\lambda\) términos de las dos primeras ecuaciones hacia el lado derecho y luego dividir la primera ecuación por la segunda.

\[ x_2 = 2 \lambda \\ x_1 = 3 \lambda \\ \frac{x_2}{x_1}=\frac{2 \lambda}{3 \lambda}\]Los\(\lambda\) términos luego se cancelan, dejándonos con dos ecuaciones (la anterior y la tercera ecuación de las tres condiciones de primer orden originales) y dos incógnitas (\(x_1\)y\(x_2\)). \[\begin{gathered} %star suppresses line # \frac{x_2}{x_1} = \frac{2}{3}\\ 100 - 2x_1 - 3x_2 = 0\end{gathered}\]La ecuación superior tiene una interpretación económica agradable. Dice que, en la solución óptima, el MRS (pendiente de la curva de indiferencia) debe igualar la relación precio (pendiente de la restricción presupuestal).

Desde la ecuación superior, podemos resolver para\(x_2\). \[x_2=\frac{2}{3}x_1\]

Luego podemos sustituir esta expresión en la ecuación inferior (la restricción presupuestaria) para obtener el valor óptimo de\(x_1\).

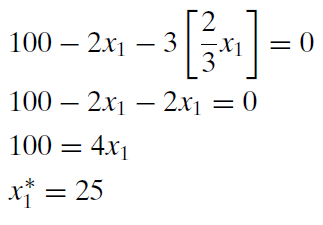
Entonces sustituimos\(x_1\mbox{*}\) en la expresión\(x_2\) para obtener\(x_2\mbox{*}\). \[x_2=\frac{2}{3}[25]\]\[x_2\mbox{*}=16\frac{2}{3}\]El asterisco se utiliza para representar la solución óptima para una variable de elección. Esta obra dice que este consumidor debe comprar 25 unidades de bien 1 y\(16 \frac{2}{3}\) unidades de bien 2 para maximizar la satisfacción dada la restricción presupuestal. Podemos usar la ecuación 1 o 2 de las condiciones originales de primer orden para encontrar el valor óptimo de\(\lambda\). De cualquier manera, obtenemos\(\lambda\mbox{*} = 8 \frac{1}{3}\).

Para muchos problemas de optimización, estaríamos interesados en conocer el valor numérico del máximo evaluando la función objetiva (en este caso la función de utilidad) en la solución óptima. Pero recordemos que la utilidad se mide sólo hasta una escala ordinal y el valor real de la utilidad es irrelevante. Queremos maximizar la utilidad, pero no nos importa su valor máximo real. El hecho de que la utilidad sea ordinal, no cardinal, también explica por qué el valor óptimo de lambda no es significativo. En general, el multiplicador lagrangeo nos dice cómo cambia el valor máximo de la función objetiva a medida que se relaja la restricción. Con la utilidad como función objetiva, esta interpretación no es aplicable.

Enfoque Numérico

En lugar de cálculo (a través del método de Lagrange) y lápiz y papel, podemos usar métodos numéricos para encontrar la solución óptima.

Para utilizar el enfoque numérico, necesitamos hacer algunos trabajos preliminares. Tenemos que configurar el problema en Excel, organizando cuidadosamente las cosas en una meta, variables endógenas, variables exógenas y restricción. Una vez que tenemos todo organizado, podemos usar el Solver de Excel para obtener la solución.

PASO Abra el libro de Excel OptimalChoice.xls, lea la hoja de introducción y luego vaya a la hoja OptimalChoice para ver cómo se puede usar el enfoque numérico para resolver el problema en el que trabajamos anteriormente.

La Figura 3.2 reproduce la pantalla que ve cuando llega por primera vez a la hoja OptimalChoice.

Figura 3.2: La visualización inicial en la hoja OptimalChoice.

Fuente: OptimalChoice.xls! OptimalChoice

Observe cómo se organiza la hoja de acuerdo a los tres componentes del problema de optimización: meta, endógena y variables exógenas. La celda de restricción muestra cuánto del presupuesto del consumidor permanece disponible para comprar bienes. El consumidor en la Figura 3.2 no está utilizando todos los ingresos disponibles por lo que sabemos que la satisfacción no se puede maximizar en el punto 20,10.

PASO Hagamos que el consumidor compre\(x_2\) con los $30 restantes. A $3/unidad, se\(x_2\) pueden comprar 10 unidades adicionales de. Ingresa 20 en la\(x_2\) celda (B13) y presiona la tecla Enter. El gráfico se actualiza para mostrar el punto 20,20, que está en la restricción presupuestal, y dibuja tres nuevas curvas de indiferencia.

Aunque 20,20 agota los ingresos disponibles, no es la solución óptima. Si bien sabes que la respuesta es 25\(16 \frac{2}{3}\),, hay otra manera de decir que el consumidor puede hacerlo mejor.

PASO Mire cuidadosamente la pantalla debajo de la tabla. Revela que el MRS no iguala la relación precio. Esto inmediatamente nos dice que algo anda mal aquí.

MRS nos\(> p_1/ p_2\) dice que la pendiente de la curva de indiferencia en ese punto es mayor que la pendiente de la restricción presupuestal. El consumidor no puede cambiar la pendiente de la restricción presupuestal, pero el MRS puede ser alterado eligiendo una combinación diferente de bienes. Este consumidor necesita bajar el MRS (en valor absoluto) para igualar a los dos. Esto se puede hacer bajando la restricción presupuestal.

Si el consumidor compra 10 más de bien 1 (así 30 unidades del\(x_1\) total), el consumo de\(x_2\) debe caer por\(6 \frac{2}{3}\) unidades a\(13 \frac{1}{3}\).

PASO Ingresa 30 en la celda B12 y la fórmula\(=13 + 1/3\) en B13. Ahora estás del otro lado de la solución óptima. El MRS es menor que la relación precio.

Podrías, por supuesto, seguir ajustando las celdas manualmente, pero hay una manera más rápida.

PASO Haga clic en la pestaña Datos en la cinta de Excel (en la parte superior de la pantalla) y haga clic en Solver (agrupado bajo la pestaña Analizar) o ejecute Herramientas: Solver en versiones anteriores de Excel para abrir el cuadro de diálogo Parámetros del Solver (que se muestra en la Figura 3.3).

Figura 3.3: Interfaz Solver de Excel.

Si no tiene Solver disponible como opción, muestre el cuadro de diálogo Administrador de complementos y asegúrese de que Solver esté en la lista y marcado. Si Solver no aparece en la lista, debe instalarlo. Solver está incluido en una instalación estándar de Excel. Para obtener ayuda, pruebe support.office.com o www.solver.com.

Observe cómo el Solver de Excel incluye información sobre la función objetivo (la celda de destino), las variables de elección (las celdas cambiantes) y la restricción presupuestaria. Todos estos han sido llenados para ti, pero aprenderás a hacerlo tú mismo en futuros trabajos.

PASO Dado que toda la información se ha ingresado en el cuadro de diálogo Parámetros del Solver, simplemente haga clic en el botón Resolver en la parte inferior del cuadro de diálogo.

El Solver de Excel funciona probando diferentes combinaciones\(x_1\)\(x_2\) y evaluando la mejora en la celda de destino, mientras intenta mantenerse dentro de la restricción. Cuando no puede mejorar mucho más, calcula que ha encontrado la respuesta y muestra un mensaje como se muestra en la Figura 3.4.

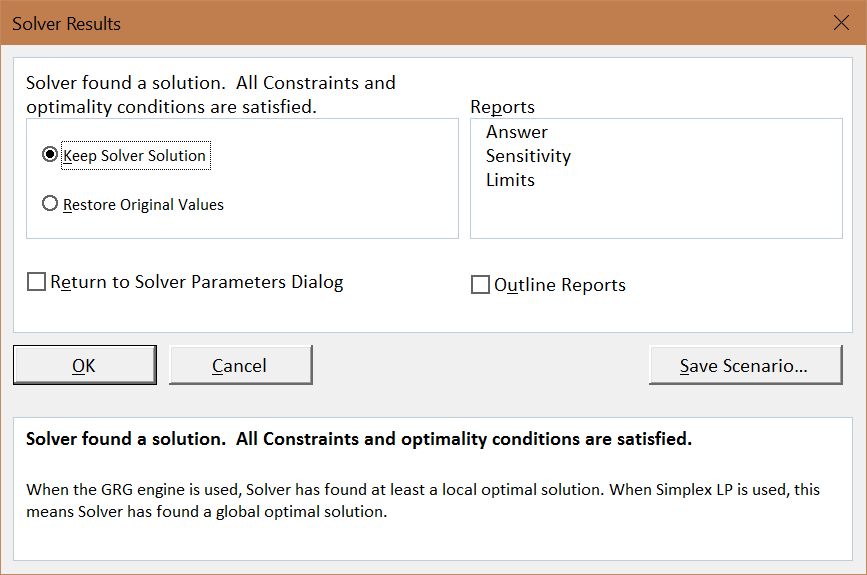Figura 3.4: Solver reporta éxito.

Si bien Solver obtiene la respuesta correcta en este problema, veremos en futuras aplicaciones que Solver no es perfecto y no merece una confianza ciega.

PASO Haga clic en la opción Sensibilidad en Informes y haga clic en Aceptar; Excel pone la solución Solver en las celdas B12 y B13. También inserta una nueva hoja en el libro de trabajo con el Informe de Sensibilidad.

PASO Haga clic en las celdas B12 y B13. Observe que Excel no obtuvo exactamente 25 y\(16 \frac{2}{3}\). Se acercó mucho y ciertamente se puede interpretar el resultado como una confirmación de la solución analítica, pero la salida de Solver requiere interpretación y pensamiento crítico por parte del usuario. Nos centraremos en el tema de la respuesta exactamente correcta más adelante.

PASO Proceder a la hoja Informe de Sensibilidad (insertada por Solver) para confirmar que este método numérico da sustancialmente el mismo valor absoluto para el multiplicador lagrangeo que encontramos a través del método Lagrangean (\(8 \frac{1}{3}\)). Posponemos la explicación de esto porque la escala ordinal de utilidad hace que la interpretación del multiplicador lagrangeo no tenga sentido. Por ahora, simplemente notamos que Solver puede reportar lambda óptima y sus resultados coincidieron con el método Lagrangean.

Podría notar que Excel reporta un valor multiplicador lagrangeo de -8.33 (con algunos 3s finales más) pero nuestro trabajo analítico no produjo un número negativo. Resulta que ignoramos el signo de\(\lambda^{*}\). Si configuramos el Lagrangean como la función objetiva menos (en lugar de más) lambda multiplicada por la restricción o reescribimos la restricción como\(0 = 2x_1 + 3x_2 - 100\) (en lugar de\(0 = 100 - 2x_1 - 3x_2\)), obtendríamos un valor negativo para\(\lambda^{*}\) en nuestro trabajo analítico. La forma en que escribimos la restricción o si sumamos o restamos la restricción es arbitraria, por lo que ignoramos el signo de\(\lambda^{*}\).

Para ser claros, a diferencia del signo, la magnitud de\(\lambda^{*}\) puede ser significativa, pero no es en esta aplicación porque la utilidad no es cardinal. Sin embargo, veremos ejemplos donde el valor de\(\lambda^{*}\) es útil y tiene una interpretación económica.

Uso de métodos analíticos y numéricos para encontrar la solución óptima

Hay dos formas de resolver problemas de optimización:

1. La forma tradicional utiliza lápiz y papel, derivados y álgebra. El método Lagrangean se utiliza para resolver problemas de optimización restringidos, como el problema de elección del consumidor.

2. Los avances en computadoras han llevado a la creación de métodos numéricos para resolver problemas de optimización. El Solver de Excel es un ejemplo de un algoritmo numérico que se puede utilizar para encontrar soluciones óptimas.

En los capítulos que siguen, seguiremos utilizando enfoques tanto analíticos como numéricos. Verás que ninguno de los dos métodos es perfecto y ambos tienen fortalezas y debilidades.

Ejercicios

La función de utilidad\(U = 10x - 0.1x^2 + y\),, tiene una forma funcional cuasilineal. Utilice esta función de utilidad para responder a las preguntas que aparecen a continuación.

1. Supongamos que la línea presupuestaria es\(100 = 2x + 3y\). Utilice el método analítico para encontrar la solución óptima. Muestre su trabajo.

2. Supongamos que el consumidor considera el bulto 0,33.33, comprando no x y gastando todos los ingresos en y. Usa el MRS comparado con la lógica de relación precio para explicar qué hará el consumidor y por qué.

3. Esta función de utilidad se puede escribir de una forma más general con letras en lugar de números, así:\(U = ax - bx^c + dy\). Si un aumenta, ¿qué sucede con el consumo óptimo de\(x\mbox{*}\)? Explica cómo llegaste a tu respuesta.

Referencias

El epígrafe es de la página 421 de A Short Relate of the History of Mathematics de W. W. W. Rouse Ball (publicado por primera vez en 1888). Por supuesto, hay muchos libros sobre la historia de las matemáticas, pero este clásico es divertido y fácil de leer. Mezcla historias sobre personas con contenido matemático real.

Todo este libro (y muchos otros) está disponible gratuitamente en books.google.com. Puedes leerlo en línea o descargarlo como archivo pdf.

Apéndice: Derivados y Optimización

Una derivada es una expresión matemática que te dice cómo y en una función\(y = f(x)\) cambia dado un cambio infinitesimalmente pequeño en x. Gráficamente, es la pendiente, o tasa de cambio, de la función a ese valor particular de x.

Las funciones lineales tienen una pendiente constante y, por lo tanto, un valor constante para la derivada. Para la función lineal\(y = 6 + 3x\), se escribe la derivada de y con respecto a x\(\frac{dy}{dx}\) (pronunciada “d y d x”) y su valor es 3. Esto te dice que cada vez que la variable x sube, la variable y sube tres veces. Entonces, si x aumenta en 1 unidad, y aumentará en 3 unidades. Esto es fácil de ver en la Figura 3.5.

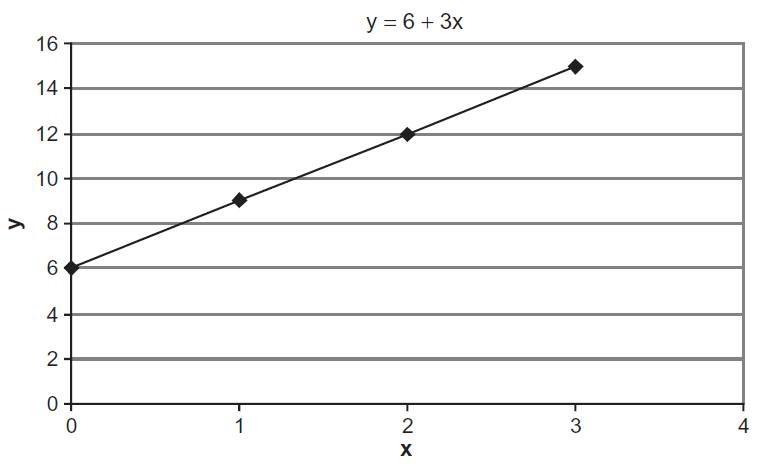Figura 3.5: Una función lineal.

Las funciones no lineales tienen una pendiente cambiante y, por lo tanto, una derivada que toma diferentes valores a diferentes valores de x. Considera la función\(y = 4x - x^2\). La Figura 3.6 grafica esta función. Su derivado es\(\frac{dy}{dx} = 4 - 2x\). Cuando se evalúa en un punto específico, como\(x = 1\), la derivada es la pendiente de la línea tangente en ese punto.

Figura 3.6: Una función no lineal con línea tangente en\(x=1\).

A diferencia del caso anterior, esta derivada tiene x en ella. Esto significa que esta función es no lineal. La pendiente depende del valor de x. At\(x=1\), la derivada es 2, pero at\(x=2\), es cero (\(4-2[2]\)) y at\(x=3\), es -2 (\(4-2[3]\)).

Además, debido a que es no lineal, el tamaño del cambio en x afecta a la tasa de cambio medida. Por ejemplo, el cambio en y de\(x = 1\) a\(x = 2\) es 1 (porque nos movemos de\(y = 3\) a a\(y = 4\) medida que aumentamos x en 1). Si aumentamos x en una cantidad menor, digamos 0.1 (de 1 a 1.1), entonces\(\frac{\Delta y}{\Delta x}=\frac{3.19-3}{1.1-1} = 1.9\). Al tomar un cambio menor en x, obtenemos una medida diferente de la tasa de cambio.

Si calculamos la tasa de cambio a través de la derivada, evaluando\(4 - 2x\) a x = 1, obtenemos 2. La derivada calcula la tasa de cambio para un cambio infinitesimalmente pequeño en x. Cuanto menor sea el cambio en x, más cerca\(\frac{\Delta y}{\Delta x}\) se acerca\(\frac{dy}{dx}\). Se puede ver que esto sucede como\(\frac{\Delta y}{\Delta x}\) pasó de 1 a 1.9 como\(\Delta x\) cayó de 1 a 0.1. Si vamos aún más pequeños, haciendo\(\Delta x\) = 0.01 (pasando de 1 a 1.01), entonces\(\frac{\Delta y}{\Delta x}=\frac{3.0199-3}{1.01-1} = 1.99\).

Optimización con la Derivada

Un problema de optimización normalmente requiere que encuentres el valor de una variable endógena (o variables) que maximice o minimice una función objetivo particular. Podemos usar derivados para encontrar la solución óptima. A esto se le llama un enfoque analítico.

Si dibujamos líneas tangentes en cada valor de x en la Figura 3.6, sólo una sería horizontal (con derivada y pendiente de cero) y esa sería la que está en la parte superior. Esto nos da una estrategia de solución: para encontrar el máximo, encontrar el valor de x con la línea tangente plana. Esto equivale a encontrar el valor de x donde la derivada es cero.

Al resolver por el valor de x donde\(\frac{dy}{dx} = 0\), encontramos la solución óptima. Porque\(y = 4x - x^2\), esto es fácil. Establecemos la derivada igual a cero y resolvemos para\(x\mbox{*}\). \[\frac{dy}{dx} = 4 - 2x\mbox{*} = 0\\ 4 = 2x\mbox{*}\\ x\mbox{*} = 2\]La ecuación que haces cuando estableces la primera derivada igual a cero se llama condición de primer orden. La condición de primer orden es diferente de la derivada porque la derivada por sí misma no es igual a nadapuedes enchufar cualquier valor de x y la expresión derivada bombeará una respuesta que te diga si y por cuánto la función está subiendo o bajando en ese punto. La condición de primer orden es una situación especial en la que estás usando la derivada para encontrar una línea tangente horizontal para averiguar dónde la función tiene un punto plano.

Una forma reducida es la respuesta que obtienes cuando la derivada se establece igual a cero y se resuelve para la solución óptima. Puede ser un número o una función de variables exógenas. No puede tener ninguna variable endógena en la expresión. A veces, no se puede resolver explícitamente para\(x\mbox{*}\). Decimos que no hay solución de forma cerrada en estos casos. La solución puede existir (y se pueden usar métodos numéricos para encontrarla), pero no podemos expresar la respuesta como una ecuación.

La segunda derivada es la derivada de la primera derivada. Te indica la pendiente de la función de pendiente. Por ejemplo, si una función tiene una pendiente constante, vimos que su primera derivada es un valor constante (como 3 en el primer ejemplo anterior). Entonces la segunda derivada es cero.

Las segundas derivadas son útiles en la optimización por la siguiente razón: cuando encuentras el valor de la variable endógena que hace que la primera derivada sea igual a cero, el punto que hayas localizado podría ser un máximo o un mínimo. Si quieres estar seguro cuál has encontrado, puedes consultar la segunda derivada. Para\(y = 4x - x^2\), la primera derivada es\(4 - 2x\) y la segunda derivada es, por lo tanto, -2. Debido a que la segunda derivada es negativa, sabemos que nuestro punto plano en x = 2 es un máximo y no un mínimo.

En este libro, no utilizaremos segundos derivados para comprobar que nuestras soluciones son verdaderamente máximas o mínimas. Nuestras funciones serán (en su mayoría) bien portadas y nos centraremos en la economía del problema, no en las matemáticas.

En resumen, los derivados se utilizan para medir la tasa de cambio de una función en base a un cambio fugantemente pequeño en x. Si establecemos una derivada igual a cero, estamos tratando de encontrar una solución óptima encontrando un valor para x donde la línea tangente sea plana. Esta estrategia de solución se basa en la idea de que un punto donde la línea tangente es horizontal debe significar que estamos en la parte superior de la función (o abajo, si estamos minimizando).

Datos útiles sobre matemáticas

Este apéndice concluye con una breve lista de reglas comunes para tomar derivados y trabajar con exponentes. La idea aquí es agudizar tus habilidades matemáticas para que puedas resolver problemas de optimización analíticamente.

Una derivada se puede calcular aplicando directamente la definitioni.e., tomando el límite del cambio en x a medida que se acerca a cero y determinando el cambio en y. Afortunadamente, sin embargo, hay una manera más fácil. Se han desarrollado reglas de diferenciación que hacen que sea mucho menos tedioso tomar un derivado. La mayoría de los libros de cálculo tienen cubiertas internas que están llenas de reglas. Muchos estudiantes nunca comprenden que estas reglas son en realidad atajos. Aquí hay una lista corta, con especial énfasis en los utilizados en economía.

A las reglas derivadas le siguen algunas reglas de álgebra relacionadas con operaciones legales sobre exponentes. Utilizaremos estas reglas a menudo para encontrar soluciones óptimas y reducir expresiones complicadas a respuestas finales más simples.

Leer estas ecuaciones es aburrido y tedioso, pero puede ahorrar mucho tiempo y esfuerzo en el futuro (especialmente si tus matemáticas están oxidadas). Deberías considerar escribir los ejemplos para un número diferente, digamos 6. Entonces, en vez de\(x^4\), ¿para qué sirve la derivada con respecto a x\(x^6\)?

Reglas Derivadas

Sea x la variable y a sea una constante.

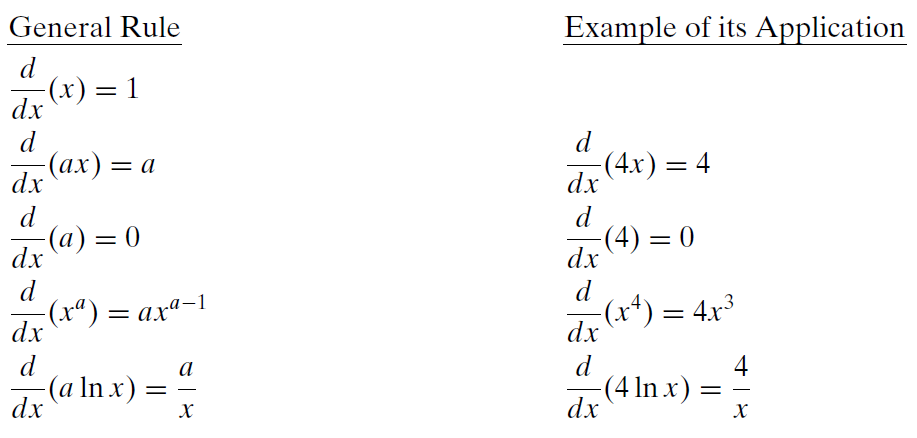
Cuando tomas una derivada de una función con respecto a una variable, aplicas las reglas a las diferentes partes de la función. Por ejemplo, si\(y = 4x - x^2\), entonces aplicas la\(\frac{d}{dx}(ax) = a\) regla a\(4x\), obteniendo 4. Aplica la\(\frac{d}{dx}(x^a) = ax^{a-1}\) regla a\(- x^2\) y obtienes\(- 2x\). Así, la derivada de y con respecto a x es\(\frac{dy}{dx} = 4 - 2x\).

Hay otras reglas de cálculo, por supuesto, como la regla de la cadena, pero las explicaremos cuando sean necesarias.

Leyes de los exponentes