3.2: Más práctica y comprensión Solver

Sabemos que existen dos enfoques para resolver problemas de optimización.

1. Métodos analíticos usando álgebra y cálculo (convencional, papel y lápiz, usando el método Lagrangean): La idea es transformar el problema de optimización restringida del consumidor en un problema sin restricciones y luego resolverlo usando la técnica estándar de cálculo no restringido. e., tomar derivados, establecer igual a cero, y resolver el sistema de ecuaciones.

2. Métodos numéricos usando una computadora (Solver de Excel): Configura el problema en Excel, organizando cuidadosamente las cosas en una meta, variables endógenas, variables exógenas y restricción; luego usa el Solver de Excel. Utilice el Informe de sensibilidad en el cuadro de diálogo Resultados del Solver para obtener\(\lambda\mbox{*}\).

En este capítulo, aplicamos ambos métodos sobre un nuevo problema.

Problema de práctica cuasilineal de utilidad

Una función de utilidad que se compone de una función no lineal de un bien más una función lineal del otro bien se denomina forma funcional cuasilineal. Es cuasi, o algo así, lineal porque un bien aumenta la utilidad de manera lineal y el otro no.

A continuación se muestra un ejemplo general y un ejemplo más específico de utilidad cuasilineal.

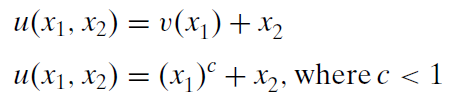
Si\(c < 1\), entonces la función de utilidad cuasilineal dice que la utilidad aumenta a una tasa decreciente a medida que\(x_1\) aumenta, pero la utilidad aumenta a una tasa constante a medida que\(x_2\) aumenta.

El problema de optimización es maximizar esta función de utilidad sujeta a la restricción presupuestal habitual. Está escrito en forma de ecuación así:\[\max\limits_{x_1,x_2,\lambda}x_1^c + x_2 \\ \textrm{s.t. } p_1x_1 + p_2x_2 = m\] Vamos a resolver la versión general de este problema, con letras que representan variables exógenas en lugar de números, usando el método Lagrangean.

1. Reescribe la restricción para que sea igual a cero.

\(0 = m - p_1x_1 - p_2x_2\)

2. Formar la función lagrangea. \[\max\limits_{x_1,x_2,\lambda} {\large\textit{L}} = x_1^c + x_2 + \lambda(m -p_1x_1 - p_2x_2)\]Tenga en cuenta que la función Lagrangean, L, tiene la función de utilidad cuasilineal más el multiplicador Lagrangean,\(\lambda\), multiplicado por la restricción reescrita.

A diferencia del problema concreto del capítulo anterior, que utilizó valores numéricos, este es un problema general con letras que indican variables exógenas. Los problemas generales, sin valores numéricos para variables exógenas, son más difíciles de resolver porque tenemos que hacer un seguimiento de muchas variables y asegurarnos de entender cuáles son endógenas versus exógenas. Si la solución se puede escribir en función de las variables exógenas, sin embargo, a menudo es fácil ver cómo una variable exógena afectará a la solución óptima.

3. Tomar derivados parciales con respecto a\(x_1\),\(x_2\), y\(\lambda\).

Recuerde que la derivada parcial trata otras variables como constantes. Así, la derivada parcial de la función de utilidad cuasilineal con respecto a no\(x_1\) tiene ninguna\(x_2\) variable en ella.

4. Establezca las derivadas iguales a cero y resuelva para\(x_1\mbox{*}\),\(x_2\mbox{*}\), y\(\lambda\mbox{*}\).

Utilizamos el mismo método de solución que antes, moviendo los términos lambda hacia el lado derecho y luego dividiendo la primera ecuación por la segunda, lo que nos permite cancelar los términos lambda.

Al cancelar los términos lambda, hemos reducido las tres ecuaciones, tres sistemas desconocidos a dos ecuaciones con dos incógnitas.

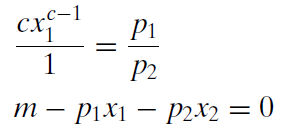
Recuerda que no todas las variables son iguales. Las variables endógenas, las incógnitas, son\(x_1\) y\(x_2\). Las otras letras son variables exógenas.

A partir de la primera ecuación, podemos resolver para la cantidad óptima de bien 1 (ver el apéndice de la sección anterior si estos pasos son confusos).

Observe que utilizamos la regla que\((x^a)^b = x^{ab}\). Porque queríamos resolver por\(x_1\), elevamos a ambos lados al\(\frac{1}{c-1}\) poder para que el\(c - 1\) exponente en\(x_1\) tiempos\(\frac{1}{c-1}\) igualara 1.

Por lo general, cuando tenemos el MRS igual a la relación precio, necesitamos resolver para una de las variables x en términos de la otra y sustituirla en la restricción presupuestal. Sin embargo, una propiedad de la función de utilidad cuasilineal es que el MRS solo depende de\(x_1\); así resolviendo for\(x_1\), obtenemos la solución de forma reducida. Al resolver un problema en términos generales, la respuesta debe expresarse como una función de las variables exógenas solas (sin variables endógenas) y esto se denomina forma reducida.

Para conseguirlo\(x_2\), simplemente sustituimos\(x_1\) en la restricción presupuestaria y resolvemos para\(x_2\).

Es un poco desordenado, pero es la respuesta. Tenemos una expresión para la cantidad óptima de\(x_2\) que es una función solo de variables exógenas.

Para obtener el valor óptimo de lambda, podemos usar la segunda condición de primer orden, que simplemente dice eso\(\lambda \mbox{*} = \frac{1}{p_2}\). Si usas la primera condición, sustituyendo en el valor por óptimo\(x_1\), tomará un poco de trabajo, pero obtendrás el mismo resultado.

Practica con la MRS =\(\frac{p_1}{p_2}\) Lógica

Los economistas enfatizan el pensamiento marginal. La idea es que, desde cualquier posición, puedas moverte y ver cómo cambian las cosas. Si hay mejoría, continúe moviéndose. La solución óptima es en un punto plano, donde la mejora es imposible.

Cuando movemos los términos lambda hacia el lado derecho y dividimos la primera ecuación por la segunda, obtenemos una declaración crucial del hecho de que la mejora es imposible y estamos optimizando.

El MRS familiar iguala la expresión de relación precio, junto con la condición de tercer primer orden, que dice que el consumidor debe estar en la línea presupuestaria (agotando todos los ingresos), es una forma matemática de describir el pensamiento marginal.

La condición MRS nos dice que si el MRS no es igual a la relación precio, existen dos posibilidades, representadas en la Figura 3.7.

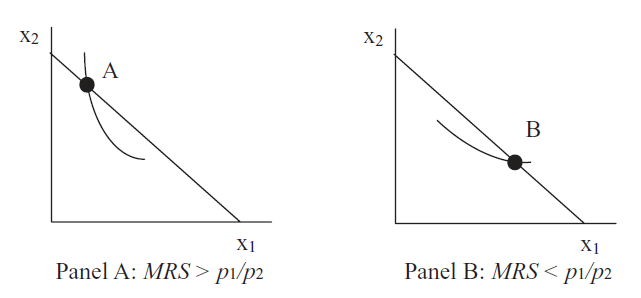Figura 3.7: MRS no iguala la relación precio.

En el Panel A, la pendiente de la curva de indiferencia en el punto A es mayor que la pendiente de la línea presupuestal (en valor absoluto). Este consumidor debe arrastrarse por la línea presupuestaria, alcanzando curvas de indiferencia más altas, hasta que el MRS iguale la relación precio. En este punto, la pendiente de la curva de indiferencia será exactamente igual a la pendiente de la línea presupuestaria y la curva de indiferencia del consumidor apenas tocará la línea presupuestaria. El consumidor no puede llegar a una curva de indiferencia más alta y mantenerse en la restricción presupuestaria. Esta es la mejor solución posible.

En el Panel B, la historia es la misma, pero invertida. La pendiente de la curva de indiferencia en el punto B es menor que la pendiente de la línea presupuestal. Este consumidor debería arrastrarse por la línea presupuestaria, alcanzando curvas de indiferencia más altas, hasta que el MRS iguale la relación precio. En este punto, la pendiente de la curva de indiferencia será exactamente igual a la pendiente de la línea presupuestaria y la curva de indiferencia del consumidor apenas tocará la línea presupuestaria.

Aproximación numérica al problema de práctica cuasilineal

PASO Abra el libro de Excel OptimalChoicePractice.xls, lea la hoja de introducción, y luego vaya a la hoja QuasiLinearchoice para ver cómo se puede usar el enfoque numérico para resolver este problema.

Es fácil ver que el consumidor no puede permitirse el paquete 5,20 dados los precios e ingresos que figuran en la hoja. Si compra cinco unidades de\(x_1\), ¿cuál es el máximo\(x_2\) que puede comprar?

PASO Ingresa esta cantidad en la celda B12. ¿El gráfico y la celda B21 confirman que lo entendiste bien?

Si ingresó 13 en B12, entonces el gráfico se actualiza y muestra que el consumidor ahora está en la línea de presupuesto. Además, la celda de restricción, B21, es ahora cero.

Sin ejecutar Solver ni hacer ningún cálculo en absoluto, ¿está maximizando a 5,13?

La respuesta es que ella no lo es. Es difícil ver en el gráfico si la curva de indiferencia está recortando la línea presupuestaria, pero la información debajo del gráfico muestra que el MRS no es igual a la relación precio. Eso te dice que la curva de indiferencia no es, de hecho, tangente a la línea presupuestal por lo que el consumidor no está optimizando. Debido a que el MRS es mayor que la relación precio (en valor absoluto) también sabemos que el consumidor debe comprar cada vez\(x_1\) menos\(x_2\), bajando por la línea presupuestal hasta que se cumpla la condición marginal. Busquemos la solución óptima.

PASO Ejecutar Solver. Seleccione el Informe de Sensibilidad para obtener\(\lambda\mbox{*}\).

¿Cómo se compara la respuesta de Excel con nuestra respuesta analítica? Recordemos que encontramos:

PASO Crear fórmulas en Excel para computar estas dos soluciones (usar las celdas C11 y C12 tendría sentido). Esto requiere un poco de cuidado con los paréntesis. Aquí está la fórmula para el bien 1: = (p1_/ (c_*p2_)) (1/ (c_-1)).

Deberías descubrir que el Solver de Excel está bastante cerca de la solución exactamente correcta, 6.25, 12.75. Se concluye que los dos métodos, analítico y numérico, coinciden sustancialmente.

Es cierto, sin embargo, que Solver está ligeramente fuera del resultado analítico calculado. En general, hay dos razones para el minúsculo desacuerdo entre los dos métodos.

1. Excel no puede mostrar el resultado algebraico a un número infinito de decimales. Si la solución es un número decimal o irracional repetido, Excel no puede manejarlo. Incluso si el número se puede expresar como un decimalpor ejemplo, la mitad es 0.5error de precisión puede ocurrir durante el cálculo de la respuesta final. Esta no es la fuente de la discrepancia en este caso.

2. El solucionador de Excel a menudo pierde la respuesta exactamente correcta por pequeñas cantidades. Solver tiene un criterio de convergencia (que se puede establecer a través del botón Opciones en el cuadro de diálogo Parámetros del Solver) que determina cuándo deja de buscar una mejor respuesta. La Figura 3.8 ofrece una representación gráfica del algoritmo de Solver en un caso de una variable.

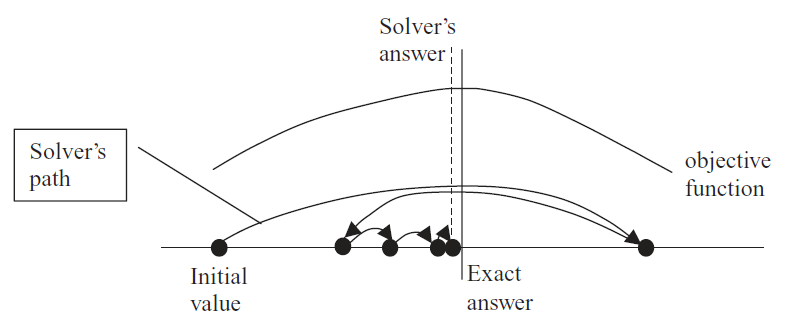Figura 3.8: Solver en acción.

El gráfico estilizado (lo que significa que representa una idea sin usar datos reales) en la Figura 3.8 muestra que Solver trabaja probando diferentes valores y viendo cuánta mejora ocurre. La ruta de la variable choice (en el eje x) está determinada por el algoritmo de optimización interna de Solver. Por defecto, utiliza el método de Newton (un algoritmo de descenso más empinado), pero puede elegir una alternativa haciendo clic en el botón Opciones en el cuadro de diálogo Solver.

Cuando Solver da un paso que mejora muy poco el valor de la función objetiva, determinado por el criterio de convergencia (ajustable a través del botón Opciones), deja de buscar y anuncia el éxito. En la Figura 3.8, a Solver le falta un poco la solución óptima porque, si acercamos el zoom, la función objetivo sería casi plana en la parte superior. Solver no puede distinguir mejoras adicionales.

Cuando decimos que el método analítico concuerda con Solver, no queremos decir que los dos métodos coincidan exactamente, sino simplemente que corresponden, en un sentido práctico. Si Solver está fuera de la respuesta exacta en el decimoquinto decimal, es decir de acuerdo, para todos los efectos prácticos.

Además, es fácil concluir que Solver debe dar una respuesta exacta porque muestra tantos decimales. Esto es incorrecto. La visualización de Solver es un ejemplo de falsa precisión. No es cierto que los muchos dígitos proporcionen información útil. La respuesta exacta es 6.25 y 12.75. Lo que estás viendo es ruido de Solver. Debes aprender a interpretar los resultados de Solver como inexactos y no reportar todos los decimales.

Hay otra manera en la que Solver nos puede fallar y es mucho más grave que interpretar incorrectamente los resultados.

Solver comportándose mal

PASO Comienza desde\(x_1 = 1, x_2 = 20\) para ver una demostración de que Solver no es perfecto. Después de fijar las celdas B11 y B12 a 1 y 20, respectivamente, ejecute Solver. ¿Qué pasa?

Un resultado miserable (un término real, técnico en la literatura de métodos numéricos) ocurre cuando un algoritmo informa que no puede encontrar la respuesta o muestra una solución obviamente errónea. La Figura 3.9 muestra un ejemplo de un resultado miserable. Solver está anunciando claramente que no puede encontrar una respuesta.

Figura 3.9: Un resultado miserable.

Si miras cuidadosamente la hoja de cálculo (haz clic en cancelar o en Aceptar si es necesario para volver a la hoja), verás que Solver explotó cuando probó un valor negativo para\(x_1\). La celda de función objetivo, B7, está mostrando el error #NUM! porque Excel no puede tomar la raíz cuadrada de un número negativo.

Para ser claros, cuando partimos de 1,20, Excel intenta moverse a la izquierda y cruza sobre el eje y hacia territorio x negativo. Dado que la función de utilidad es\(x_1^{0.5}\), intenta tomar la raíz cuadrada de un número negativo, produciendo un error y fallando el algoritmo.

Cuando Solver falla, existen tres estrategias básicas para solucionar el problema:

1. Pruebe diferentes valores iniciales (en las celdas cambiantes). Si sabes aproximadamente dónde se encuentra la solución, empieza cerca de ella. Evite siempre comenzar desde cero o una celda en blanco.

2. Agregar más estructura al problema. Incluir restricciones de no negatividad en las variables endógenas, si procede. En el caso de la teoría del consumidor, si sabes que el comprador no puede comprar montos negativos, agrega esta información.

3. Reorganizar completamente el problema. En lugar de optimizar directamente, puedes poner Solver a trabajar en ecuaciones que deben cumplirse. En este problema, usted sabe que\(= \frac{p_1}{p_2}\) se requiere MRS. Podrías crear una celda que sea la diferencia entre el MRS y la relación precio y hacer que Solver encuentre los valores de la variable choice que fuercen a esta celda a ser igual a cero.

Probemos la segunda estrategia.

PASO Restablezca los valores iniciales a 1 y 20, luego inicie Solver (haga clic en la pestaña Datos y haga clic en Solver) y haga clic en el botón Agregar (en la parte superior de los botones apilados a la derecha).

Solver responde apareciendo el cuadro de diálogo Agregar restricción.

PASO Seleccione ambas variables endógenas en el campo Referencia de celda\(>=\), seleccione e ingrese 0 en el campo Restricción para que el cuadro de diálogo se vea como Figura 3.10. Haga clic en Aceptar.

Figura 3.10: Un resultado miserable.

Se devuelve al cuadro de diálogo principal Parámetros de Solver, pero se ha agregado la restricción de que las celdas B11 y B12 deben ser no negativas.

Puede notar que podría haber hecho clic simplemente en la opción Crear variables no restringidas no negativas, pero agregar la restricción muestra cómo trabajar con restricciones.

PASO Una vez que vuelva al cuadro de diálogo principal Parámetros del Solver, haga clic en Resolver.

Esta vez, Solver tiene éxito. Agregar la restricción de no negatividad evitó que Solver intentara\(x_1\) valores negativos y produjera un error.

Completos Perfectos Problema de Práctica

Recordemos que las curvas de indiferencia en forma de L representan complementos perfectos, que se reflejan a través de la siguiente función matemática:

\[u(x_1,x_2) = min{ax_1,bx_2}\]Supongamos\(a = b = 1\) y la línea presupuestaria es\(50 = 2x_1 + 10x_2\).

Primero, queremos resolver este problema analíticamente.

El método Lagrangean no se puede aplicar porque la función no es diferenciable en la esquina de la L. El método Lagrangean, sin embargo, no es el único método analítico disponible. La Figura 3.11 muestra que cuando a = b = 1, la solución óptima debe estar sobre un rayo del origen con pendiente +1.

Figura 3.11: La línea de solución óptima con complementos perfectos.

La solución óptima tiene que estar en la esquina de las curvas de indiferencia en forma de L porque un punto no esquinero (ya sea en la parte vertical u horizontal de la curva de indiferencia) implica que el consumidor está gastando dinero en más de uno de los bienes sin obtener ninguna satisfacción adicional. Así, sabemos que la solución óptima debe estar en la línea\(x_2 = x_1\).

Podemos combinar esta ecuación de solución óptima con la restricción presupuestaria para encontrar la solución óptima. Las dos ecuaciones, dos sistemas desconocidos se pueden resolver fácilmente por sustitución.

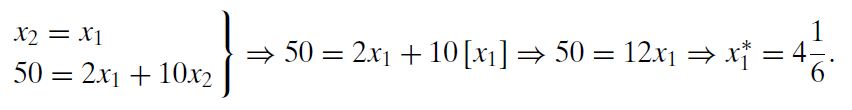
Por supuesto, sabemos\(x_2 = x_1\) que lo óptimo también\(x_2\) es\(4 \frac{1}{6}\). ¿Excel puede hacer este problema y obtenemos la misma respuesta? Vamos a averiguarlo.

PASO Procede a la hoja PerfectComplements para ver cómo configuramos la hoja de cálculo en Excel. Haga clic en la celda B7 para ver la función de utilidad.

STEP Ejecute Solver y obtenga un Informe de Sensibilidad. Solver puede ser utilizado para generar un valor para el multiplicador lagrangeo (a través del Informe de Sensibilidad) aunque no pudiéramos usar el método lagrangeo en nuestro trabajo analítico.

Al igual que con el problema anterior (con utilidad cuasilineal), encontramos que Solver y el enfoque analítico coinciden sustancialmente. La respuesta es un decimal repetido, por lo que Excel no puede obtener la respuesta exacta\(4 \frac{1}{6}\), pero está muy cerca.

Anteriormente, vimos que Solver podía chocar y dar un resultado miserable. Ahora, aprendamos que Solver realmente puede portarse mal.

PASO A partir de\(x_1 = 1, x_2 = 1\), ejecute Solver. ¿Qué pasa?

Estás viendo un ejemplo de un resultado desastroso que ocurre cuando un algoritmo informa que ha encontrado la respuesta, pero está mal. No hay un error obvio y el usuario bien puede aceptar la respuesta como verdadera.

Solver reporta un resultado exitoso, pero la respuesta que da es 1,1 y sabemos que la respuesta correcta es\(4 \frac{1}{6}\) para ambos bienes.

Los resultados desastrosos incluyen un elemento de interpretación. En este caso, podríamos notar que 1,1 está muy dentro de la restricción presupuestal y, por lo tanto, el algoritmo ha fallado. Un resultado verdaderamente desastroso ocurre cuando no hay forma de probar o verificar independientemente la respuesta incorrecta del algoritmo.

Los resultados miserables y desastrosos están bien definidos, términos técnicos en la literatura matemática sobre métodos numéricos. Los resultados desastrosos son mucho más peligrosos que los resultados miserables. Estos últimos son frustrantes porque la computadora no puede dar una respuesta, pero resultados desastrosos llevan al usuario a creer una respuesta que en realidad es incorrecta. En el mundo de la optimización numérica, son un hecho de la vida. Los métodos numéricos no son perfectos. Nunca debes confiar completamente en ningún algoritmo de optimización.

Comprensión de SolVerbe Skeptical

Este capítulo permitió la práctica de resolver el problema de optimización restringida del consumidor con dos funciones de utilidad diferentes, una función cuasilineal y complementos perfectos. En ambos casos, encontramos que el Solver de Excel coincidía, prácticamente hablando, con el método analítico.

La capacidad de resolver problemas de optimización con dos métodos independientes significa que podemos estar realmente seguros de que hemos encontrado una solución óptima cuando dan las mismas respuestas.

Además, exploramos cómo funciona realmente Solver. Evalúa la función objetiva para diferentes valores de las variables de elección. Continúa buscando una mejor solución hasta que no puede mejorar mucho (una cantidad determinada por el criterio de convergencia).

Solver puede fallar al informar que no puede encontrar una solución (llamada resultado miserable) o peor al informar una respuesta incorrecta sin error obvio (lo cual es un resultado desastroso).

Es fácil creer que un resultado mostrado por una computadora está garantizado para ser correcto. No seas descuidado y confiandolos métodos numéricos pueden fallar y fallan, a veces espectacularmente.

Este punto merece una cuidadosa repetición. Ejecuta Solver y felizmente anuncia que se ha encontrado una solución y ofrece hasta un número de 15 o 16 dígitos para su inspección. El problema, sin embargo, es que la solución está muy alejada. No en la millonésima ni en la décima cifra decimal, sino completamente, totalmente equivocada. Cómo podría suceder esto nos lleva demasiado lejos en la tierra de la optimización numérica, pero basta con decir que siempre debes preguntarte si la respuesta tiene sentido común.

Solver realmente es una forma poderosa de resolver problemas de optimización, pero no es perfecta. Siempre hay que recordar esto. Después de ejecutar Solver, formatee los resultados con miras a la facilidad de comprensión y piense en el resultado en sí. No aceptes sin pensar un resultado de Solver. Mantente alerta incluso si Solver afirma haber golpeado pagar sucio ¡puede ser un resultado desastroso!

Más explicación de Solver está disponible en el archivo SolverInstructions.doc en la carpeta SolverCompStaticSwizard.

Ejercicios

1. En el ejemplo cuasilineal de este capítulo, utilice la primera ecuación en las condiciones de primer orden para encontrar\(\lambda\mbox{*}\). Muestre su trabajo.

2. Utilice métodos analíticos para encontrar la solución óptima para el mismo problema de complementos perfectos que se presenta en este capítulo, excepto que\(a = 4\) y\(b = 1\). Muestre su trabajo.

3. Dibuja una gráfica (usando las Herramientas de Dibujo de Word) de la solución óptima para la pregunta anterior.

4. Usa el Solver de Excel para confirmar que tienes la respuesta correcta. Toma una foto de las celdas que contienen tu objetivo, variables endógenas y variables exógenas.

Referencias

A medida que la economía se volvió más matemática, nació un nuevo curso, Math Econ. El curso necesitaba libros y R. G. D. Allen's Mathematical Analysis for Economists (publicado por primera vez en 1938) se convirtió en un libro de texto clásico. Como dijo E. Schneider, un revisor, “Este libro llena una necesidad largamente sentida. Por fin poseemos un libro que presenta el aparato matemático necesario para un estudio serio de la economía en una forma adecuada a las necesidades del economista”. Véase The Economic Journal, Vol. 48, núm. 191 (septiembre de 1938), p. 515. El epígrafe es de la página 2 de Análisis matemático para economistas, ya que Allen discute cómo y por qué las matemáticas se pueden aplicar al estudio de la economía.