4.6: Efectos de Ingresos y Sustitución

Sin duda, la curva de demanda es la idea más importante en la Teoría del Comportamiento del Consumidor. Hemos derivado la curva de demanda analítica y numéricamente. La curva de demanda nos indica la cantidad óptima para comprar a un precio determinado. También nos dice cómo va a cambiar la cantidad demandada a medida que cambie el precio, ceteris paribus.

Esta sección se mantiene enfocada en la curva de demanda, extendiendo el análisis de la respuesta óptima del consumidor ante un cambio en el precio. El concepto central es que el efecto total sobre la cantidad demandada (dada por la curva de demanda) para un cambio dado en el precio se puede desglosar en dos efectos separados, llamados efectos de ingreso y sustitución.

Nuestra atención sigue en el cambio en la cantidad demandada como cambios de precios, ceteris paribus, pero al romper la respuesta observada cuando cambia el precio, obtenemos una explicación más profunda de la demanda. También explicamos cómo podríamos conseguir un Giffen bueno.

Intuición

Antes de sumergirnos en gráficas complicadas y matemáticas, repasemos la historia detrás de los efectos de ingresos y sustitución. Ver el panorama general mejora tus posibilidades de entender realmente de qué se tratan los ingresos y los efectos de sustitución.

Supongamos que, ceteris paribus, el precio sube. Sabemos que el consumidor tiene que reoptimizar. Sabemos que el consumidor elegirá una nueva combinación óptima de bienes. Podemos ver que el consumidor compra una cantidad diferente después de los cambios de precio. Si simplemente calculamos el cambio en la cantidad comprada de\(x_1\) antes y después del cambio de precio, estamos comparando dos puntos en la curva de demanda. A esto se le llama el efecto total de un cambio de precio.

La idea revolucionaria es que el incremento en el precio tiene dos canales por los cuales afecta al consumidor. Un canal se centra en el hecho de que un aumento de precio es como una disminución del poder adquisitivo. Después de todo, dado un nivel de ingresos, si los precios se duplican, entonces puedo comprar la mitad de lo que compré antes. Mis ingresos no han cambiado, pero mi poder adquisitivo ha caído igual que si mis ingresos se hubieran reducido a la mitad. El efecto ingreso refleja el hecho de que los cambios de precios afectan la cantidad óptima demandada al alterar el poder adquisitivo.

El otro canal se llama el efecto de sustitución. La idea es que un cambio de precio en un bien altere los precios relativos que enfrenta el consumidor e induzca la sustitución del bien relativamente más barato por el relativamente más caro. Cuando\(p_1\) sube,\(x_1\) es relativamente más caro que\(x_2\) y así que naturalmente voy a evitar\(x_1\) y sentirme atraído por\(x_2\).

La Figura 4.17 muestra los dos canales por debajo del efecto totalestán sumergidos y no se observan directamente. Sumado en conjunto, conforman el efecto total.

Figura 4.17: La idea básica detrás de los efectos de ingresos y sustitución.

Veremos que el efecto ingreso puede ser positivo o negativo, pero el efecto de sustitución siempre es negativo (asumiendo preferencias de buen comportamiento). Cuando el precio sube, el efecto de sustitución dice “compre menos”. Por supuesto, si el precio cae, ocurre lo contrario y, solo de acuerdo con el efecto de sustitución, aumenta el consumo.

La razón por la que el efecto ingreso es ambiguo en señal es el hecho de que hay bienes normales e inferiores. Si el bien es normal, entonces los\(x_1\) aumentos óptimos a medida que aumentan los ingresos, pero si el bien es inferior, entonces el consumo y los ingresos están inversamente relacionados.

Finalmente, ayuda a conocer la motivación subyacente detrás del descubrimiento de los efectos de ingresos y sustitución. Los economistas estaban discutiendo sobre la existencia de bienes Giffen. La Ley de la Demanda dijo que el precio y la cantidad estaban inversamente relacionados. Efectos de ingreso y sustitución explicados bajo qué condiciones es posible el comportamiento de Giffen (una curva de demanda ascendente). Veremos que si los efectos de ingreso y sustitución funcionan juntos, entonces se garantiza que la curva de demanda sea descendente. Comprender los efectos de ingresos y sustitución nos permitirá dar una definición más refinada y precisa de la Ley de la Demanda.

Ejemplo Numérico de Efectos de Ingresos y Sustitución

PASO Abra el libro de Excel IncSubEffects.xls, lea la hoja de introducción y continúe con la hoja OptimalChoice.

Tenemos la función habitual de Cobb-Douglas con una línea presupuestal convencional. Ya hemos hecho este problema antes y la solución óptima inicial es 25,\(16 \frac{2}{3}\).

\(p_1\)PASO Disminución de 1 a $1/unidad (en la celda B17).

La Figura 4.18 muestra lo que hay en su pantalla. La línea roja es la nueva línea presupuestaria familiar (después de la disminución del precio). Hay, sin embargo, una línea discontinua que no se ha utilizado antes. Esta línea discontinua representa el resultado de un experimento mental.

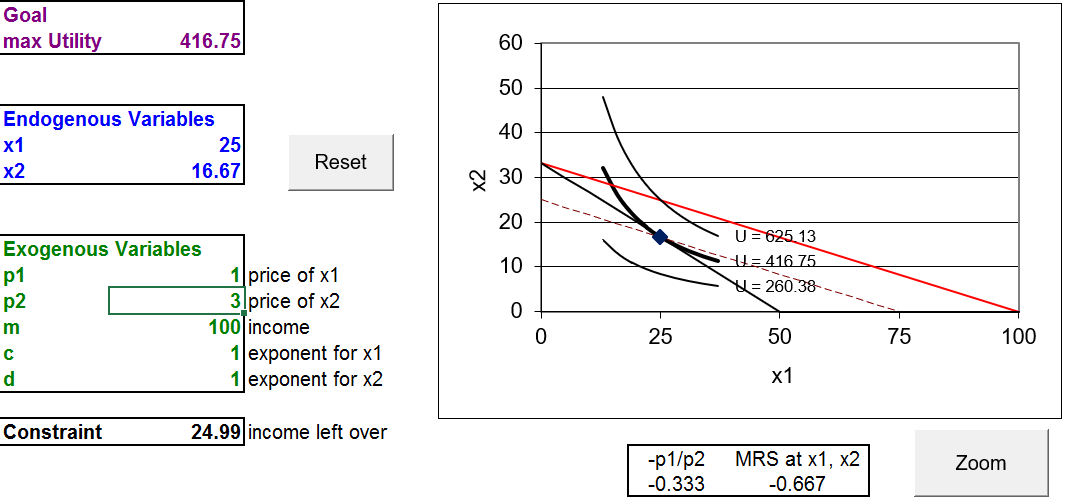
Figura 4.18: Disminución\(p_1\).

Fuente: IncSubEffects.xls! OptimalChoice

PASO Haga clic en el botón para ver una segunda gráfica de la situación. Tiene la escala de ejes ajustada para que puedas ver mejor lo que está pasando.

La línea discontinua es fundamental para comprender la división del efecto total en efectos de ingreso y sustitución. Tiene la misma pendiente que la nueva línea presupuestal, sin embargo, pasa por la solución óptima inicial. Lo que hemos hecho es pretender quitarle suficientes ingresos al consumidor para permitirle comprar el paquete inicial con el nuevo, inferior\(p_1\).

Nos quitamos ingresos (bajando la restricción presupuestaria en relación con la nueva línea presupuestaria) porque la caída del precio implica un incremento en el poder adquisitivo. Si hubiera habido una subida de precios, habríamos tenido que incrementar los ingresos para compensar el incremento de precios.

Encontraremos una solución de tangencia en la línea discontinua y esto nos permitirá dividir el efecto total en los efectos de ingreso y sustitución.

Por supuesto, nada como esto realmente sucede en el mundo real. Cuando el precio baja, el consumidor vuelve a optimizar, comprando un nuevo paquete óptimo, y ese es el final de la historia. Pero a los efectos de entender la curva de demanda, averiguamos qué compraría el consumidor en la línea discontinua imaginaria y la usamos para dividir el efecto total en los efectos de sustitución e ingreso.

Pero todo esto es demasiado abstracto. Hagámoslo de hecho para que veas cómo funciona. Para averiguar cuánto ingreso tomar para cancelar el poder adquisitivo cambiado del cambio de precio, utilizamos la Ecuación del Ajustador de Ingresos. \[\Delta m = x_1 \mbox{*}\Delta p_1\]Aplicado a este problema, sabemos que\(x_1 \mbox{*}\) es 25 (desde la solución óptima inicial) y el cambio en\(p_1\) es\(-1\) (porque el precio bajó de 2 a 1, así\(new - initial\) es\(1 - 2\)); así, tenemos:\[\Delta m = x_1 \mbox{*}\Delta p_1\] \[\Delta m = [25][-1] = -25\]El menos nos dice que tenemos que quitarnos ingresos. La línea discontinua se basa en un ingreso de $75,\(p_1 = 1\), y\(p_2 = 3\).

En resumen, tenemos tres líneas presupuestales cuando trabajamos con efectos de ingreso y sustitución: (1) la línea inicial habitual, (2) la nueva línea habitual a partir del cambio de precio, y (3) la línea imaginaria (discontinua) que se ha ajustado para pasar por la solución óptima inicial.

Encontramos la nueva solución óptima habitual para poder calcular primero el efecto total, luego usamos la línea discontinua para encontrar los efectos de ingreso y sustitución.

PASO Con\(p_1 = 1\), ejecute Solver.

La Figura 4.19 muestra que el consumidor elige la\(16 \frac{2}{3}\) combinación 50,. Así, tenemos dos puntos a considerar hasta el momento:

• Punto A: Inicial: At\(m = 100, p_1 = 2, x_1 \mbox{*} = 25, x_1 \mbox{*} = 16 \frac{2}{3}\).

• Punto C: Nuevo: At\(m = 100, p_1 = 1, x_1 \mbox{*} = 50, x_1 \mbox{*} = 16 \frac{2}{3}\).

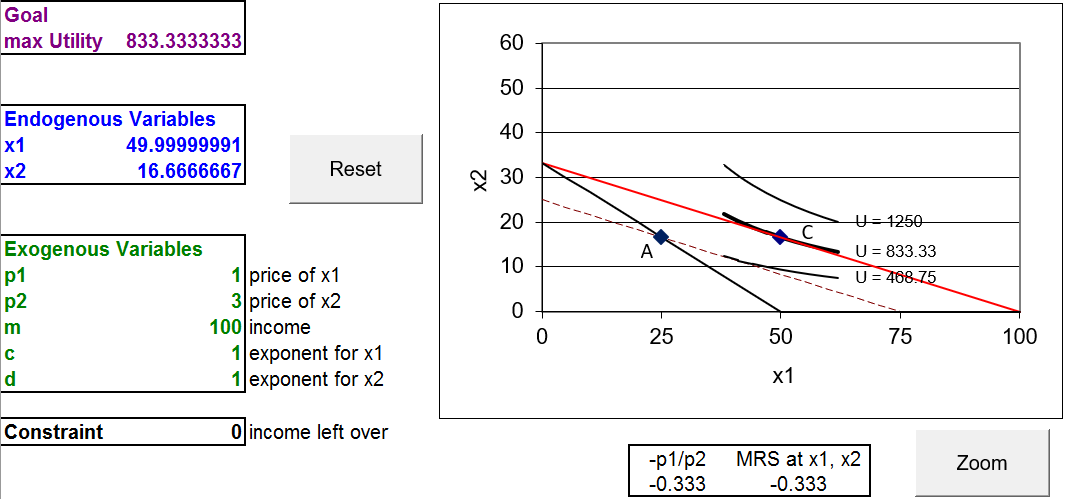
Figura 4.19: Nueva solución óptima en\(p_1 = 1\).

Fuente: IncSubEffects.xls! OptimalChoice

Observe que Excel muestra tres curvas de diferencia alrededor de la solución óptima actual, pero en realidad hay un número infinito de curvas que atraviesan cada punto del cuadrante. \(c = d = 1\)Al mantenerse constante, el mapa de indiferencia no está cambiando de ninguna manera. Simplemente estamos mostrando diferentes curvas de indiferencia cuando\(x_1\) y\(x_2\) en las celdas B12 y B13 cambian.

Los puntos A y C son dos puntos en la curva de consumo de precios y dos puntos en la curva de demanda. El efecto total de una disminución de $1/unidad en el precio del bien 1 se puede encontrar midiendo el movimiento de A a C: para\(x_1\), el efecto total es\(+25\) unidades y para\(x_2\), el efecto total es cero (\(x_2 \mbox{*} = 16 \frac{2}{3}\)antes y después del choque de precios).

El efecto total se puede observar directamente. Con el precio inicial, podemos ver que el consumidor compra 25 unidades de buena 1 y\(16 \frac{2}{3}\) de buena 2. Vemos el precio del bien 1 caer por $1 por unidad y ver al consumidor responder comprando 25 unidades más de\(x_1\) y dejando la cantidad de\(x_2\) sin cambios.

Ya estamos listos para el movimiento clave. Hipotéticamente quitaremos exactamente 25 dólares de ingresos para que podamos encontrar la solución óptima en la línea imaginaria y discontinua. Al consumidor en realidad no se le quitan ingresos. Se trata de un experimento de pensamiento. Elaborar lo que haría el consumidor en esta hipotética situación nos permite dividir el efecto total en sus partes constituyentes.

PASO Cambie los ingresos a 75 dólares (observe que la línea presupuestaria ahora se encuentra encima de la línea presupuestal discontinua) y ejecute Solver.

Puede ignorar con seguridad la línea más pronunciada en el chartall que queremos es el punto B, la solución óptima con la línea de presupuesto discontinua. Solver nos dice que el punto B es 37.5,12.5. Esto nos da tres puntos a considerar:

• Punto A: Inicial: At\(m = 100, p_1 = 2, x_1 \mbox{*} = 25, x_2 \mbox{*} = 16 \frac{2}{3}\).
• Punto B: No observado: At\(m = 75, p_1 = 1, x_1 \mbox{*} = 37 \frac{1}{2}, x_2 \mbox{*} = 12 \frac{1}{2}\).
• Punto C: Nuevo: At\(m = 100, p_1 = 1, x_1 \mbox{*} = 50, x_2 \mbox{*} = 16 \frac{2}{3}\).

Observe cuidadosamente los tres puntos y concéntrese en cómo difieren los puntos B y C: C usa nuevo\(p_1\) con m original, mientras que B se basa en nuevo\(p_1\) con m ajustado (ajustado de manera especial para que la línea discontinua pase por el punto A).

Con estos tres puntos, podemos calcular el total, ingresos, y efectos de sustitución para\(x_1\) y\(x_2\). Los tres efectos se muestran mediante flechas en los ejes de la Figura 4.20. Esta es una gráfica complicada. Tómate tu tiempo y léelo con cuidado. Trate de separar los diferentes elementos y líneas a diferentes partes del problema: inicial (A), nueva (C) e intermedia (B).

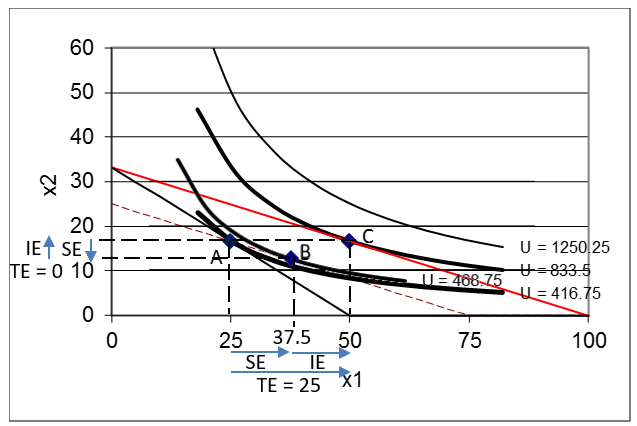Figura 4.20: Efectos totales (TE), ingresos (IE) y sustitución (SE).

Hay efectos medidos de un punto a otro para ambos\(x_1\) y\(x_2\). Estos\(\Delta\) s se calculan de la manera habitual como\(new - initial\). Para\(x_1\), encontramos:

• SE: A a B:\(37 \frac{1}{2} - 25 = 12 \frac{1}{2}\)
• IE: B a C:\(50 - 37 \frac{1}{2} = 12 \frac{1}{2}\)
• TE: A a C:\(50 - 25 = 25\)

Observe que el efecto total (TE) se puede encontrar calculando la diferencia de A a C (\(50 - 25 = 25\)) o aprovechando que SE + IE = TE, así\(12.5 + 12.5 = 25\). Todos los efectos para\(x_1\) se calculan a lo largo del eje x en términos de unidades de\(x_1\).

Analizar el efecto sobre\(x_2\) un cambio en nos\(p_1\) da ingresos cruzados y efectos de sustitución para\(x_2\), los cuales se muestran mediante flechas en el eje y, en la Figura 4.20.

• SE: A a B:\(12 \frac{1}{2} - 16 \frac{2}{3} = - 4 \frac{1}{6}\)
• IE: B a C:\(16 \frac{2}{3} - 12 \frac{1}{2} = 4 \frac{1}{6}\)
• TE: A a C:\(16 \frac{2}{3} - 16 \frac{2}{3} = 0\)

En\(x_2\), los efectos de ingreso y sustitución funcionan uno contra el otro. El efecto de sustitución, de A a B, disminuye la cantidad de\(x_2\) desde que\(p_1\) cayó, haciéndose\(x_2\) más caro en relación con\(x_1\). Pero cuando pasamos de B a C, el efecto ingreso cancela exactamente a la SE. La caída en\(p_1\) ha aumentado nuestro poder adquisitivo y, como\(x_2\) es un bien normal, queremos comprar más de él.

Es una propiedad de la función de utilidad Cobb-Douglas que los efectos cruzados IE y SE se cancelan entre sí, dejando un efecto total cero. Este no es un resultado habitual o común y demuestra cómo la forma funcional impone estructura a la curva de demanda.

Volvamos ahora\(x_1\) y centrémonos en su efecto de sustitución, que sabemos que siempre es negativo. Esto lleva inmediatamente a una pregunta: Si la SE siempre es negativa, entonces ¿por qué está\(+12.5\) en la Figura 4.20?

La respuesta a esta aparente contradicción es que lo negativo se refiere a la relación, no al valor real de la SE. Dado que el precio bajó, un incremento en la cantidad comprada es consistente con un efecto negativo porque es la relación entre las dos variables la que se está describiendo como negativa.

De igual manera, el signo del efecto ingreso puede ser complicado. La clave es prestar atención a qué variable de choque se está considerando. El efecto ingreso medido como respuesta a un cambio en el ingreso es positivo, en este caso, porque a medida que paso de B a C, mi ingreso se incrementa y respondo incrementando mi consumo óptimo de bien 1.

Ahora podría preguntarse: “Si los dos efectos funcionan juntos, entonces, ¿cómo es negativo el efecto de sustitución y el efecto ingreso positivo?” Esto se debe a que definimos el efecto ingreso como la respuesta a un cambio en los ingresos, como el movimiento del punto B al C en la Figura 4.20. Pero, si recuerdas, este ejemplo comenzó con una disminución en el precio del bien 1. La disminución en el precio del bien 1 puede interpretarse como un incremento en los ingresos, en el sentido de mayor poder adquisitivo. Si vinculamos el incremento 12.5 en el bien 1 del efecto ingreso a la disminución del precio del bien 1, vemos que esta relación negativa refuerza el efecto de sustitución negativa y da un efecto total negativo.

Ahora que sabemos cómo se combinan los efectos de ingreso y sustitución para formar el efecto total de un cambio de precio, podemos mostrar lo fácil que es calcularlos a partir de una solución de forma reducida.

Primero tenemos que resolver el modelo analíticamente y obtener una expresión de forma reducida en función de\(m\) y\(p_1\). Hemos hecho esto antes para una función de utilidad Cobb-Douglas y encontramos\[x_1 \mbox{*} = (\frac{c}{c+d})\frac{m}{p_1}\] Si sustituimos en\(c=d=1\), tenemos\[x_1 \mbox{*} = \frac{m}{2p_1}\] At\(m=100\) y\(p_1=2\),\(x_1 \mbox{*}=25\). Esta es la solución inicial (punto A).

Si\(p_1\) cae a $1/unidad, entonces enchufamos\(m=100\) y\(p_1=1\), lo que da la nueva solución (punto C),\(x_1 \mbox{*}=50\). El efecto total es\(50 - 25 = 25\).

Para encontrar el SE, necesitamos el punto B. Utilizamos la expresión de forma reducida para calcular la cantidad demandada con m ajustado ($75) y nuevo\(p_1\) ($1/unidad). \[x_1 \mbox{*} = \frac{m}{2p_1} = \frac{[75]}{2[1]} = 37.5\]Una vez que tenemos el punto B, hemos dividido el efecto total de A a C y podemos calcular el SE e IE pasando de A a B y B a C, respectivamente. El SE es\(37.5 - 25 = 12.5\) y el IE es\(50 - 37.5 = 12.5\). Estos resultados concuerdan con nuestro trabajo anterior.

Efectos de Ingresos y Sustitución vía Gráficas

Los efectos de ingresos y sustitución son complicados. La Figura 4.20 no es fácil de entender. Hay tres líneas presupuestales y están pasando muchas cosas. Entonces, ¿qué es tan importante de los efectos de ingresos y sustitución que hace que valga la pena dominarlos?

Los efectos de ingresos y sustitución son la clave para explicar cómo podemos conseguir un bien Giffen. Marcan avances reales en la economía, asentando un largo debate sobre si son posibles o no curvas de demanda con pendiente ascendente. Desconstruiremos la gráfica de ingresos y efectos de sustitución (Figura 4.20), examinando cada capa una a la vez, para mostrar la fuente del comportamiento de Giffen.

Comenzamos con la Figura 4.21. A la izquierda tenemos la solución óptima inicial y la derecha muestra un solo punto en la curva de demanda (no mostrado).

Figura 4.21: La solución inicial.

A continuación, disminuimos el precio del bien 1, como se muestra en la Figura 4.22, lo que crea una nueva línea presupuestal. Sabemos que el consumidor reoptimizará y elegirá una nueva solución óptima a lo largo de la nueva línea más plana, pero la Figura 4.22 aún no muestra esta nueva solución. En cambio, muestra la solución del punto B en línea discontinua con los ingresos que habría que quitar para cancelar el aumento del poder adquisitivo de la disminución del precio.

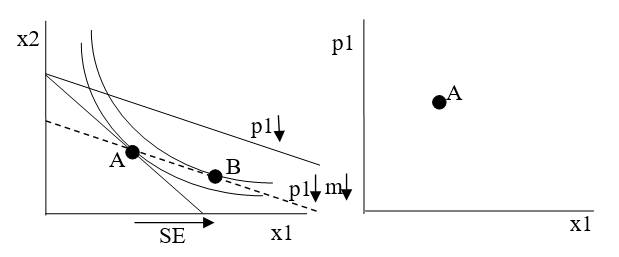Figura 4.22:\(p_1\) Disminución y restricción presupuestal imaginaria.

La Figura 4.22 muestra la solución óptima, punto B, para la situación hipotética con m menor\(p_1\) y ajustada. La flecha hacia la derecha es la SE para\(x_1\) es el efecto de sustitución, del punto A al B en el eje x. La línea discontinua tiene una pendiente más plana (nueva\(p_1\) es menor que la inicial\(p_1\)) a través del punto A. Esto garantiza que B está a la derecha de A. Es por ello que la SE siempre es negativa.

Es imposible dibujar un punto B a la izquierda de A sin hacer cruzar las curvas de indiferencia. Con MRS =\(\frac{p_1}{p_2}\) a A, bajar\(p_1\) y ajustar m para que la línea discontinua pase por A, significa que el consumidor debe desplazarse hacia el sureste para encontrar la curva de indiferencia más alta tangente a la línea discontinua.

Ahora, estamos listos para mostrar el punto C. Tenemos un conocido efecto de sustitución negativa y todo lo que queda por hacer es encontrar la curva de indiferencia tangente a la nueva línea presupuestal (con menor\(p_1\)). La visión clave es que existen varias posiciones posibles para el punto C. La figura 4.23 muestra tres posibilidades.

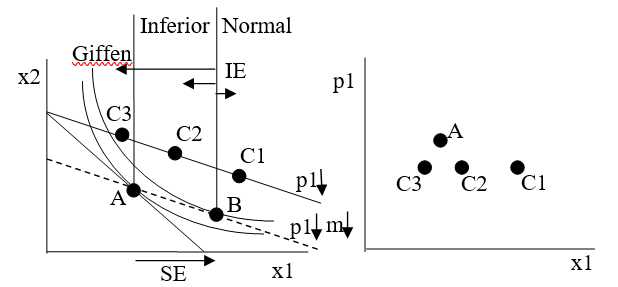Figura 4.23: Comprensión del comportamiento de Giffen.

La figura 4.23 muestra que la posición final del punto C depende de si el bien es normal o inferior, con una subcategoría de bienes inferiores que son Giffen.

• C1: Bueno 1 es un bien normal por lo que el efecto ingreso de B a C funciona junto con el movimiento de A a B y terminamos en el punto C1. En este caso, y para cualquier punto C a la derecha de B, obtenemos una curva de demanda en pendiente descendente.

• El bien 1 es un bien inferior por lo que los efectos de ingreso y sustitución funcionan uno contra el otro. El movimiento de B a C será a la izquierda y nos dejará con un punto C a la izquierda de B. Hay dos posibilidades:

  1. C2: El efecto ingreso empuja al consumidor a comprar menos\(x_1\), pero es menor que el efecto de sustitución (lo que lleva a comprar más a\(x_1\) medida que\(p_1\) cae). Terminamos en el punto C2 entre A y B y la curva de demanda sigue en pendiente descendente.

  2. C3: El efecto ingreso no sólo funciona en contra del efecto de sustitución, es más fuerte, inundándolo. El punto B a C se mueve en dirección opuesta a A a B y es mayor que A a B. Esto deja al consumidor a la izquierda de B en el punto C3. La curva de demanda es de pendiente ascendente. Esto es un bien Giffen.

Puede ser difícil dibujar un bien Giffen correctamente porque las curvas de indiferencia no pueden cruzar. Entonces, en la Figura 4.23, el espacio disponible para el punto C3 es ajustadoC3 solo puede caber a la izquierda de A y a la derecha de la curva de indiferencia que se muestra tangente a B.

La figura 4.23 también deja claro que son las curvas de indiferencia, que provienen de la función de utilidad, las que determinan cómo la cantidad demandada responde a un cambio en el precio. Cómo un bien genera utilidad (es decir, si la utilidad es Cobb-Douglas, cuasilineal, complementos perfectos u otra forma funcional) determina si es normal, inferior o Giffen.

La descomposición del efecto total en efectos de ingreso y sustitución proporciona la condición que debe mantener para el comportamiento Giffen: el efecto ingreso debe funcionar contra el efecto de sustitución y ser mayor. Podemos reforzar esta visión clave con una expresión matemática que brinde más detalles sobre exactamente cómo obtenemos Giffenness.

La ecuación de Slutsky

En 1915, décadas después del supuesto manchado de un bien Giffen durante la hambruna irlandesa de papa, Eugen Slutsky publicó un artículo en una revista italiana que mostraba cómo descomponer el efecto total de un cambio de precio en efectos de ingresos y sustitución. ¡Tenía una expresión matemática que mostraba cómo era posible obtener una curva de demanda con pendiente ascendente!

Desafortunadamente, su trabajo pasó desapercibido. Veinte años después, John R. Hicks (premio Nobel en 1972) y R. G. D. Allen redescubrieron las ideas en la ponencia de Slutsky. En ocasiones, la idea de ingresos y efectos de sustitución se conoce como Slutsky-Hicks o Slutsky-Hicks-Allen. Lo mantendremos simple y lo llamaremos la Ecuación de Slutsky.

La Ecuación de Slutsky, que no vamos a derivar, dice en términos matemáticos algo que ya sabemos: El efecto total de un cambio de precio puede expresarse como la suma de una sustitución y un efecto ingreso. Resulta que hay varias formas de expresar la descomposición con una Ecuación de Slutsky. Aquí hay dos versiones:\[\frac{\Delta x_1}{\Delta p_1}=\frac{\Delta x_1^{SE}}{\Delta p_1}+\frac{\Delta x_1^{IE}}{\Delta p_1}\]\[\frac{\Delta x_1}{\Delta p_1}=\frac{\Delta x_1^{SE}}{\Delta p_1}-x_1 \mbox{*}\frac{\Delta x_1}{\Delta m}\] Ambas ecuaciones dicen lo mismo: el efecto total,\(\frac{\Delta x_1}{\Delta p_1}\), es igual al efecto de sustitución,\(\frac{\Delta x_1^{SE}}{\Delta p_1}\), más el efecto ingreso. Donde difieren es cómo expresan el efecto ingreso.

Observe atentamente a los denominadores. El efecto ingreso en la primera ecuación tiene un\(\Delta p_1\) denominador, al igual que los otros dos términos. Lo que Slutsky descubrió fue que el efecto ingreso del cambio de precio,\(\frac{\Delta x_1^{IE}}{\Delta p_1}\), podría escribirse como\(-x_1 \mbox{*}\frac{\Delta x_1}{\Delta m}\). Es decir, el canal de efecto ingreso del cambio de precio se puede expresar como la cantidad de bien 1 inicialmente comprado veces el cambio en a\(x_1\) medida que cambia el ingreso (la pendiente de la curva de Engel). Observe el signo menos, que recoge el hecho de que cuando el precio baja, eso es como un incremento en los ingresos.

Ahora realmente podemos ver cómo conseguir un bien Giffen, que tiene una curva de demanda con pendiente ascendente así\(\frac{\Delta x_1}{\Delta p_1} > 0\). Desde el primer término, el efecto de sustitución siempre es negativo, definitivamente necesitamos un bien inferior para\(\frac{\Delta x_1}{\Delta m} < 0\) que para que el segundo término sea positivo. Obviamente, si el bien es extremadamente inferior, así que eso\(\frac{\Delta x_1}{\Delta m}\) es mucho menos que cero, podríamos conseguir un bien Giffen.

Pero la Ecuación de Slutsky revela otra forma de obtener el comportamiento de Giffen. Un gran efecto de ingreso contrario se puede obtener por el bien siendo inferior y el consumidor comprando mucho de él por lo que\(-x_1 \mbox{*}\frac{\Delta x_1}{\Delta m}\) es un gran número positivo para superar el efecto de sustitución negativa. Si el bien es meramente inferior, pero el consumidor compra poco de él, entonces es menos probable que sea Giffen.

Es por ello que buscamos el comportamiento de Giffen en los productos básicos, materias primas básicas que comprenden una gran parte del presupuesto. Las papas para los irlandeses, el arroz para los asiáticos y las tortillas para los mexicanos son tres ejemplos que los economistas han examinado para determinar el comportamiento de Giffen. Para una persona pobre, estos artículos podrían consumirse en grandes cantidades, sin embargo, a medida que aumentan los ingresos, la cantidad demandada cae por lo que son bienes inferiores. La combinación de un término grande\(x_1 \mbox{*}\) y\(\frac{\Delta x_1}{\Delta m} < 0\) podría producir un\(-x_1 \mbox{*}\frac{\Delta x_1}{\Delta m}\) término grande, positivo que es mayor que el efecto de sustitución negativa.

¿Recuerdas cómo generamos el comportamiento de Giffen con GiffenGoods.xls en la sección anterior? Aumentamos el precio de $1/unidad a $1.1/unidad y óptimo\(x_1\) subió de 44 a 48.6, mientras que óptimo\(x_2\) cayó dramáticamente de 11 a alrededor de 1.5. Observe cómo\(x_1\) es un elemento básico, dominando los montos comprados de los dos bienes.

Conocemos su Giffen, pero\(x_1\) también es inferior? Vamos a averiguarlo.

PASO Abra GiffenGoods.xls y proceda a la hoja Optimal1. Haga clic en el botón y ejecute Solver para asegurarse de que está en la solución inicial óptima de 44,11. Incrementa m a 60 y ejecuta Solver. ¿Qué pasa?

Sí, como sabemos debe ser cierto (ya que sabemos que\(x_1\) es un bien Giffen),\(x_1\) es un bien inferior: óptimo\(x_1\) cayó (a 39) ya que los ingresos aumentaron a $60. El giffenness requiere que\(x_1\) sea inferior y este ejemplo refleja también el hecho de que la concentración del presupuesto del consumidor en un bien inferior contribuye a la producción de una respuesta Giffen.

La hoja de Biblio en GiffenGoods.xls, de la sección anterior, tenía varias referencias a trabajos que intentaban encontrar bienes Giffen, sin embargo, el jurado aún está fuera. Lo que es incuestionable, sin embargo, es el requisito teórico: debe ser un bien inferior para que el IE esté en sentido opuesto y mayor que el SE.

La Ecuación de Slutsky también nos permite afinar una afirmación que es, estrictamente hablando, falsa. Estudiantes de economía introductoria de todo el mundo aprenden la Ley de la Demanda: cuando el precio aumenta, ceteris paribus, la cantidad demandada debe caer. En otras palabras, manteniendo todo lo demás constante, la cantidad demandada y el precio están inversamente relacionados y la demanda siempre está en pendiente a la baja.

Esto está bien, a nivel introductorio, donde no queremos confundir a los estudiantes principiantes, pero sabemos que es posible una curva de demanda con pendiente alcista, se le llama un bien Giffen. Son una violación a la “Ley” de la Demanda y sabemos que podrían existir. Cuando su precio sube, también lo hace la cantidad demandada.

¿Podemos rehabilitar la Ley de Demanda para que no haya excepción? Sí, podemos. Nuestro conocimiento de ingresos y efectos de sustitución señala el camino. Podemos definir con mayor precisión la Ley de la Demanda. Al insertar una cláusula calificadora, podemos conseguir que la Ley de Demanda sea exactamente correcta: Si el bien es normal, entonces la cantidad demandada baja a medida que sube el precio, ceteris paribus. Eso se garantiza que sea cierto porque un bien normal tiene un efecto de ingresos que funciona en conjunto con el efecto de sustitución. Así, no hay manera de conseguir Giffenness.

La función de utilidad Cobb-Douglas no puede dar comportamiento a Giffen. La solución de forma reducida\(x_1 \mbox{*} = (\frac{c}{c+d})\frac{m}{p_1}\),, significa que\(\frac{dx_1 \mbox{*}}{dm} = (\frac{c}{c+d})\frac{1}{p_1} > 0\) así el efecto ingreso,\(- x_1 \mbox{*}\frac{dx_1 \mbox{*}}{dm}\), es negativo. Esto significa que IE y SE son negativos y trabajan juntos, por lo que no hay forma de que la función de utilidad Cobb-Douglas pueda generar Giffenness.

TE = SE + ES DECIR

Los economistas utilizan los efectos de ingreso y sustitución para comprender mejor la curva de demanda y explicar el comportamiento de Giffen. Al desmontar el efecto total de un cambio de precio, la Ecuación de Slutsky muestra cómo puede surgir un bien Giffen si el efecto ingreso se opone y pantanea el efecto de sustitución (que genera una relación de pendiente ascendente entre precio y cantidad demandada).

Dada una función de utilidad y restricción presupuestaria, encontramos la solución óptima inicial (punto A). Un cambio de precio conducirá a una nueva solución óptima (punto C) que podemos usar para calcular el efecto total. Entonces podemos usar la Ecuación del Ajustador de Ingresos para encontrar un punto hipotético B que divide el efecto total en efectos de sustitución e ingresos.

Dada una expresión de forma reducida de\(x \mbox{*} = f(p,m)\), podemos encontrar los puntos A, B y C evaluando la expresión en los valores apropiados de p y m para calcular los puntos A, B y C.

La ecuación de Slutsky es una presentación matemática de los efectos de ingresos y sustitución. La matemática nos da la idea de que el efecto ingreso\(-x_1 \mbox{*}\frac{\Delta x_1}{\Delta m}\),, se compone de\(x_1\) tiempos óptimos iniciales la respuesta de\(x_1\) a un cambio de ingresos. Esto revela que la giffenness es más probable que se encuentre en bienes inferiores que también atraen una alta concentración del presupuesto del consumidor.

Hay incluso más formas de expresar la Ecuación de Slutsky que las dos utilizadas en esta sección. En lugar de alterar los ingresos para permitir que el consumidor compre el paquete inicial de bienes, puede cambiar los ingresos para permitir que el consumidor esté en la curva inicial de indiferencia. Esto a veces se conoce como el efecto de sustitución de Hicks.

Ejercicios

1. Reproduzca, usando las Herramientas de Dibujo de Word, las Figuras 4.21, 4.22 y 4.23, explicando cada gráfica con sus propias palabras.
2. Repita la pregunta 1, con un cambio clave: aplicar un incremento de precio en el 1 bueno (en lugar de una disminución de precio).
3. Al exponer la Ley de la Demanda, algunos economistas optan por incluir una condición de que el bien sea normal, así: Si el bien es un bien normal, entonces el precio y la cantidad demandada están inversamente relacionados, ceteris paribus. ¿Por qué se necesita la cláusula del bien normal?
4. Dada la función de demanda\(x_1 \mbox{*} = 20 + \frac{m}{20p_1}\),, computar los efectos totales, ingresos y sustitución cuando el precio cae de $5 a $4/unidad, con ingresos de $1000. Muestre su trabajo.
5. Utilice la hoja Optimal1 en GiffenGoods.xls para encontrar los puntos A, B y C para un choque\(p_1\) de $1 a $1.1/unidad. Compute el TE, SE e IE para\(x 1\). Muestre su trabajo y explique lo que hizo.

Referencias

El epígrafe es de la biografía de Slutsky disponible en el sitio web Historia del Pensamiento Económico de la Nueva Escuela, www.hetwebsite.net/het/. El sitio fue creado y es mantenido por Gonçalo L. Fonseca. Hay bocetos de cientos de economistas, vínculos con otros recursos y descripciones de diversas escuelas de pensamiento en economía. La historia intelectual de la economía es fascinante y este sitio web es un lugar maravilloso para navegar.