Presentamos la Teoría de Búsqueda con un Modelo de Búsqueda de Muestras Fijo. Un consumidor toma muestras de la población de tiendas y obtiene una lista de n precios para un producto, luego elige el precio mínimo. Cuanto mayor n, menor es el precio mínimo en la lista, pero el precio pagado para obtener las cotizaciones de precios aumenta a medida que n sube. El consumidor tiene que decidir cuántos precios obtener.
Esta sección explora las propiedades de una situación diferente que se conoce como el Modelo de Búsqueda Secuencial. A diferencia de la búsqueda fija de muestras, donde el consumidor obtiene un conjunto de cotizaciones de precios y luego elige el precio más bajo, la búsqueda secuencial procede de una a la vez. El consumidor toma muestras de la población y obtiene un solo precio, luego decide si aceptarlo o no. Si lo rechaza, no puede volver atrás. Como muestra el epígrafe, el modelo de búsqueda secuencial se aplica fácilmente a las ofertas de trabajo, pero se aplicará en este capítulo a otro problema de búsqueda común comprando gas.
Configuración del modelo
Imagina que estás conduciendo por la carretera y necesitas combustible. Mientras conduces, hay gasolineras (digamos N = 100) a izquierda y derecha (tomar una izquierda no te molesta demasiado) y puedes leer fácilmente el precio por galón mientras conduces hasta cada estación. Si pasas por una estación, dar la vuelta está fuera de discusión (hay tráfico y tienes una extraña fobia a los giros en U).
Hay una estación de menor precio y las estaciones pueden clasificarse de 1 (más bajo, mejor precio) a 100 (más alto, peor precio). No se sabe los precios subiendo porque las estaciones se distribuyen aleatoriamente en la carretera. La estación de precio más bajo podría ser 18 o 72 nd o incluso la primera. La figura 7.7 lo resume todo.
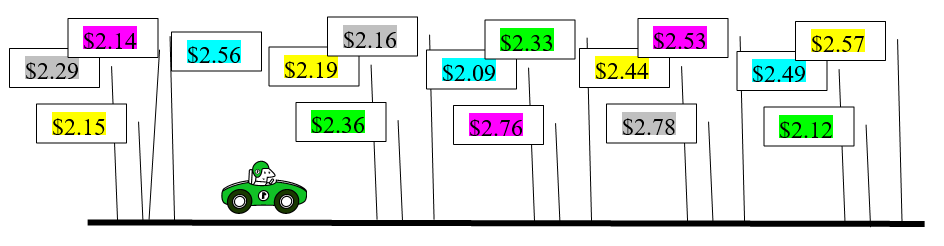Figura 7.7: Decidir dónde comprar gas.
Supongamos que te enfocas en la siguiente pregunta: ¿Cómo maximizas las posibilidades de encontrar la estación más barata?
Podrías argumentar que deberías conducir por todas las estaciones, y luego simplemente elegir la mejor. Esta es una idea terrible porque no puedes volver atrás (recuerda, no hay giros en U). Una vez que pasas por una estación, no puedes regresar a ella. Entonces, esta estrategia sólo funcionará si la estación más barata es la última. Las posibilidades de eso son 1 en un 100.
Una estrategia para elegir una estación es así: Escoja algún número\(K < N\) donde rechace (conduzca por) las estaciones 1 a K, luego elija la primera estación que tenga un precio más bajo que la más baja de las K estaciones que rechazó.
¿Quizás K = 50 es la respuesta correcta? Es decir, conduzca por las estaciones 1 a 50, luego mire la siguiente (51 st) estación y si es mejor que la más baja de las 50 por las que condujo, tire adentro. Si no, pásalo y considera la 52 ª estación. Si es más barato que la 51 anterior (o 1 a 50 ya que sabemos que la estación 51 no es más barata que la más barata de las primeras 50), consigue gasolina ahí.
Continúa con este proceso hasta que llegues gas a alguna parte, tirando a la última (100 ª) estación si llegas a ella (tendrá un letrero que diga, “Gasolinera de última oportunidad”).
Esta estrategia fallará si el precio más bajo está en el grupo de las estaciones K por las que pasaste, por lo que es posible que quieras elegir K para que sea pequeña. Pero si eliges K demasiado pequeño, obtendrás solo unos pocos precios y la primera estación con un precio más bajo que la más baja de las estaciones K es poco probable que te dé el precio más bajo.
Entonces, K = 3 probablemente no va a funcionar bien porque probablemente no obtendrás un precio súper bajo en un conjunto de solo tres así que probablemente no terminarás eligiendo el precio más bajo. Por ejemplo, digamos que las tres primeras estaciones están en el puesto 41, 27 y 90. Entonces en cuanto veas una estación mejor que 27, vas a jalar ahí. Eso podría ser 1, pero con 26 posibilidades, eso no es probable.
Por otro lado, un alto valor de K, digamos 98, sufre de que la estación de menor precio probablemente esté en ese grupo y ¡ya la rechazaste! Sí, este problema es ciertamente complicado.
El Modelo de Búsqueda Secuencial se puede utilizar para mucho más que comprar gasit tiene una aplicabilidad extremadamente amplia y, en matemáticas, se le conoce como parada óptima. En la contratación, se llama el problema de la secretaria. Una firma elige a los primeros K solicitantes, los entrevista y los rechaza, luego elige al siguiente aspirante que sea mejor que el mejor de los K aspirantes. También se aplica a muchas otras áreas, incluyendo matrimoniobúsqueda en línea para Kepler parada óptima para ver cómo el famoso astrónomo eligió a su cónyuge.
PASO Abra el libro de Excel SequentialSearch.xls y lea la hoja de introducción, luego proceda a la hoja de Configuración.
La Columna A tiene las 100 estaciones clasificadas del 1 al 100. La estación de menor precio es 1, y la estación de mayor precio es 100.
PASO Haga clic en el botón. Baraja las estaciones, distribuyéndolas aleatoriamente por la carretera que recorres en la columna D.
La celda B7 reporta dónde se encuentra la estación de menor precio (#1). Las columnas C y D reportan la ubicación de cada estación. La columna D cambia cada vez que hace clic en el botón porque las estaciones se barajan.
La celda F2 establece el valor de K. Esta es la variable de elección en este problema. Nuestro objetivo es determinar el valor de K que maximice la probabilidad de que obtengamos la estación de menor precio.
Al abrir, K = 10. Pasamos por las estaciones 1 a 10, luego tomamos la siguiente estación que es mejor que la mejor de las 10 estaciones que rechazamos.
PASO Haga clic en el botón. Esto rediseña las estaciones y dibuja un borde en la columna D para la celda en la estación K th.
La celda F5 reporta la mejor de las estaciones K (que fueron rechazadas). La celda F7 muestra la estación en la que terminaste.
PASO Desplázate hacia abajo para ver por qué terminaste en esa estación y lee el texto de la hoja.
La celda F7 siempre muestra la primera estación que es mejor (más baja) que la mejor de las K estaciones en la celda F5.
PASO Repetidamente haga clic en el botón. Después de cada clic, mira cómo te fue. ¿10 es una buena opción para K?
La definición de una buena elección en este caso es aquella que tiene una alta probabilidad de darnos la estación más barata. Nuestro objetivo es maximizar las posibilidades de conseguir la estación más barata. Podríamos tener un objetivo diferente, por ejemplo, minimizar el precio promedio pagado, pero esto sería un problema de optimización diferente. Para la versión clásica del problema de parada óptima, contamos el éxito solo cuando encontramos la estación más barata.
PASO Cambie K a 60 (en F2) y haga clic repetidamente en el botón. ¿Es 60 mejor que 10?
Esto es difícil de responder con la hoja de configuración. Tendrías que presionar repetidamente el botón y hacer un seguimiento del porcentaje de veces que obtuviste la estación más barata. Eso requeriría mucha paciencia y tiempo tediosamente haciendo clic y grabando el resultado. Afortunadamente, hay una mejor manera.
Resolviendo el problema a través de la simulación de
La hoja de configuración es una buena manera de entender el problema, pero no es útil para averiguar el valor óptimo de K. Necesitamos una forma de muestrear y registrar el resultado de forma rápida y repetida. Eso es lo que hace la hoja de McSim.
PASO Proceder a la hoja McSim y revisarla.
Con N = 100 (podemos cambiar este parámetro más adelante), establecemos el valor de K (en la celda D7) y ejecutamos una simulación de Monte Carlo para obtener las posibilidades aproximadas de obtener la mejor estación (reportada en la celda H7).
A diferencia del complemento McSim utilizado en la sección anterior, esta simulación de Montecarlo está cableada en este libro de trabajo. Por lo tanto, es extremadamente rápido.
PASO Con N = 100 y K = 10, haga clic en el botón. El número predeterminado de repeticiones es de 50 mil, lo que parece alto, pero una computadora puede hacer cientos de miles de repeticiones en cuestión de segundos.
En la Figura 7.8 se muestran los resultados. Elegir K = 10 nos da la mejor estación cerca de 23.4% de las veces. Tus resultados serán ligeramente diferentes.
Figura 7.8: Resultados de simulación Monte Carlo.
Fuente: SequentialSearch.xls! McSim
Observe que estamos utilizando la simulación de Monte Carlo para aproximar la respuesta exacta. La simulación de Monte Carlo no puede darnos la respuesta exacta. Al aumentar el número de repeticiones, mejoramos la aproximación, acercándonos cada vez más, pero nunca podremos obtener la verdad exacta con la simulación. La respuesta que da depende de los resultados reales en esa carrera en particular. La única forma en que la simulación daría la respuesta exacta es si se basara en un número infinito de repeticiones.
¿Podemos hacerlo mejor que conseguir la mejor estación cerca del 23% del tiempo?
Podemos responder a esta pregunta explorando cómo las posibilidades de obtener el precio más bajo varían con K. Al cambiar el valor de K y ejecutar una simulación de Monte Carlo, podemos evaluar el desempeño de diferentes valores de K.
PASO Explora diferentes valores de K y rellena la tabla en celdas J3:M10.
En cuanto haces la primera entrada en la tabla, K = 20, ves que supera a K = 10.
PASO Utilice los datos de la tabla rellenada para crear un gráfico de las posibilidades de obtener la estación de menor precio en función de K. Usa el botón debajo de la mesa para revisar tu trabajo.
¿Qué concluye de este análisis?
Un problema con la simulación de Montecarlo es la variabilidad en los resultados. Cada ejecución da diferentes respuestas ya que cada ejecución es una aproximación a la respuesta exacta basada en los resultados obtenidos. Así, parece bastante claro que el valor óptimo de K está entre 30 y 40, pero usar la simulación para encontrar la respuesta exacta es difícil.
La Figura 7.9 muestra los resultados de series de experimentos de Monte Carlo. Observe que duplicamos el número de repeticiones para aumentar la resolución. El mejor valor de K parece ser 36, pero el ruido en los resultados de la simulación hace imposible determinar la respuesta.
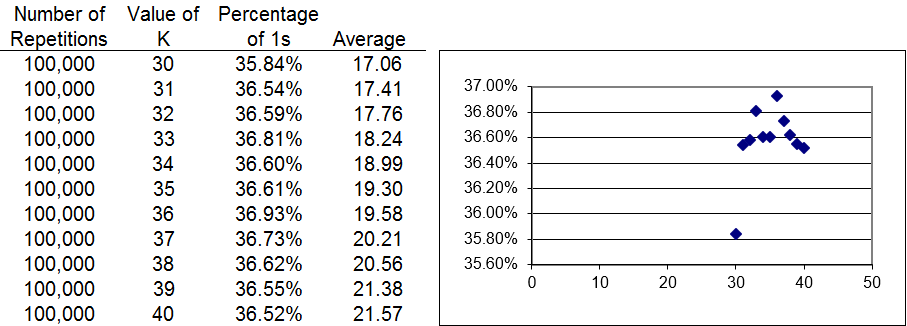
Figura 7.9: Acercar el valor de K óptimo.
Fuente: SequentialSearch.xls! RESPUESTAS
Con la simulación Monte Carlo, podemos seguir incrementando el número de repeticiones para mejorar la aproximación.
PASO Proceda a la hoja Respuestas para ver más resultados de simulación.
La hoja Respuestas muestra que hasta 1,000,000 de repeticiones no son suficientes para darnos definitivamente la respuesta correcta. La simulación está teniendo dificultades para distinguir entre un valor K de parada de 36 o 37.
Una solución exacta
Este problema se puede resolver analíticamente. La solución se implementa en Excel. Para los detalles, consulte la cita de Ferguson al final de este capítulo.
PASO Proceda a la hoja Analítica para ver la probabilidad exacta de obtener la estación más barata para una muestra dada del tamaño K de N estaciones de 5 a 100.
Por ejemplo, la celda G10 muestra 32.74%. Esto significa que tienes una probabilidad de 32.74% de obtener la estación más barata de 10 estaciones si conduces por las primeras seis estaciones y luego eliges la siguiente estación que tenga un precio menor que la más barata de las estaciones K por las que pasaste.
Para N = 10, ¿es K = 6 la mejor solución?
No. La probabilidad de elegir la estación más barata aumenta si eliges K = 5. Las opciones de 3 y 4 están cerca, pero claramente, óptima K = 3 (con una probabilidad de 39.87% de obtener la estación más barata) es la mejor opción.
En el ejemplo en el que hemos estado trabajando, teníamos N = 100. Las simulaciones de Monte Carlo mostraron K óptima alrededor de 36 o 37, pero estábamos teniendo problemas para localizar la respuesta exacta correcta.
PASO Desplázate hacia abajo para ver las probabilidades de N = 100. Haga clic en las celdas AL100 y AM100 para ver los valores exactos. La visualización se ha redondeado a dos decimales (porcentaje), pero el cálculo es preciso a más decimales.
K * = 37 apenas supera a K = 36. El hecho de que casi den exactamente las mismas posibilidades de obtener el precio más bajo explica por qué estábamos teniendo tantos problemas para acercar la respuesta correcta con la simulación de Monte Carlo.
Se puede mostrar (ver la fuente de Ferguson en la sección Referencias) que K óptima es\(\frac{N}{e}\), dando una probabilidad de encontrar la estación más barata de\(\frac{1}{e}\). Para N = 100,\(\frac{N}{e} \approx 36.7879\).
Si K fuera una variable endógena continua,\(\frac{N}{e}\) sería la solución óptima. Pero no lo es, así que la respuesta exacta, correcta es pasar las primeras 37 estaciones y luego tomar la primera con un precio menor que el precio más bajo de las estaciones 1 a 37.
Es un misterio por qué el número trascendental e, base de logaritmos naturales, juega un papel en la solución.
La Figura 7.10 muestra que a medida que el N sube, también lo hace el K óptimo. ¿Qué elasticidad se está considerando aquí?
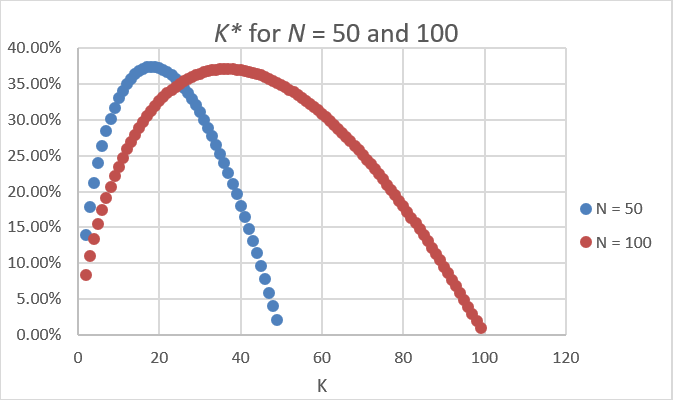
Figura 7.10: Probabilidades exactas de encontrar la estación más barata.
Fuente: SequentialSearch.xls! Analítica
La respuesta es la elasticidad N de K. De N = 50 a 100 es un incremento del 100%. ¿Qué sucede con la K óptima? Va del 18 al 37, por lo que un poco más de un 100%. La elasticidad es ligeramente superior a una. Si usa la versión continua de K, entonces K exactamente también se duplica y la elasticidad N de K es exactamente una.
Lecciones de Búsqueda Secuencial
A diferencia del Modelo de Búsqueda de Muestras Fijo (donde obtienes un conjunto de precios y eliges el mejor), el Modelo de Búsqueda Secuencial dice que dibujas observaciones de muestra una tras otra. Esto podría aplicarse a una decisión de elegir una gasolinera. Al conducir por la carretera, decide si se da la vuelta y obtener gasolina en la Estación X o pasar por esa estación y proceder a la Estación Y.
Ante la dispersión de precios, un conductor que decide dónde obtener gas puede modelarse como resolver un Modelo de Búsqueda Secuencial. Si bien puede haber otros objetivos (como obtener el precio promedio más bajo), el objetivo podría ser maximizar las posibilidades de obtener el precio más bajo. Encontramos que a medida que el N sube, también lo hace el K óptimo. Cuantas más estaciones, más manejo debes hacer antes de elegir una estación.
Al igual que el Modelo de Búsqueda de Muestras Fijas, el Modelo de Búsqueda Secuencial no tiene ninguna interacción entre empresas y consumidores. Se da dispersión de precios y se utiliza el modelo para analizar cómo reaccionan los consumidores en el entorno dado.
En los días previos a internet y smartphone, decidir dónde conseguir gasolina fue todo un reto. Un conductor que pasaba señales con precios (como la Figura 7.7) era una representación bastante precisa del entorno. No había mapas de Google ni aplicaciones que mostraran precios a tu alrededor. Observe, sin embargo, que la Ley de Un Precio aún no se aplica a los precios de la gasolina.
Ferguson señala que nuestro Modelo de Búsqueda Secuencial (que los matemáticos llaman el problema de la secretaria) forma parte de una clase de problemas de horizonte finito. “Hay una gran literatura sobre este problema, y un libro, Problemas de la mejor selección (en ruso) de Berezovskiy y Gnedin (1984) dedicado exclusivamente a él” (Ferguson, capítulo 2).
Muestra fija y modelos de búsqueda secuencial son simplemente la punta del iceberg. Existe una vasta literatura y muchas aplicaciones en la economía de la búsqueda, la economía de la información y la economía de la incertidumbre.
Ejercicios
Utilice los resultados de la hoja Analítica para calcular la elasticidad N de K * de N = 10 a 11. Muestra tu trabajo.
Utilice los resultados de la hoja Analítica para dibujar una gráfica de K * en función de N. Copia y pega tu gráfica en un documento de Word.
Ejecute una simulación Monte Carlo que admita una de las combinaciones N - K * en la hoja Analítica. Tome una foto de los resultados de su simulación y péguela en un documento de Word.
Explique por qué la simulación de Montecarlo no pudo replicar exactamente el porcentaje de veces que se encontró la estación de menor precio.
Referencias
El epígrafe es de las páginas 115 y 116 de J. J. McCall, “Economía de la información y la búsqueda de empleo”, The Quarterly Journal of Economics, Vol. 84, núm. 1 (febrero de 1970), pp. 113—126, www.jstor.org/stable/1879403. Este trabajo muestra que la búsqueda secuencial (con recuerdo) domina la búsqueda de muestras fijas. Para más información sobre este punto, véase Robert M. Feinberg y William R. Johnson, “La superioridad de la búsqueda secuencial: un cálculo”, Revista Económica del Sur, Vol. 43, núm. 4 (abril de 1977), pp. 1594—1598, www.jstor.org/stable/i243526.
Thomas Ferguson, Parada óptima y aplicaciones está disponible gratuitamente en línea en www.math.ucla.edu/ tom/Stopping/Contents.html. Ferguson ofrece una presentación técnica y matemática de la teoría de búsquedas.
C. J. McKenna, The Economics of Uncertainty (Nueva York: Oxford University Press, 1986), es una introducción concisa y no técnica a los modelos de información imperfectos.
John Allen Paulos, Beyond Numeracy (Nueva York: Alfred A. Knopf, 1991), p. 64, discute el problema óptimo de la entrevista con un estilo fácil e intuitivo.
Figura 7.7: Decidir dónde comprar gas.
botón. Baraja las estaciones, distribuyéndolas aleatoriamente por la carretera que recorres en la columna D.
botón. Esto rediseña las estaciones y dibuja un borde en la columna D para la celda en la estación K th.
botón. Después de cada clic, mira cómo te fue. ¿10 es una buena opción para K?
botón. El número predeterminado de repeticiones es de 50 mil, lo que parece alto, pero una computadora puede hacer cientos de miles de repeticiones en cuestión de segundos.
