11.1: Solución Inicial

La minimización de costos de entrada es uno de los tres problemas de optimización que enfrenta la firma. Gira en torno a la cuestión de elegir la mejor combinación de entradas, L y K, para producir un determinado nivel de salida, q.

La mejor combinación se define como la más barata. La idea es que muchas combinaciones de L y K puedan producir una q dada. Queremos conocer las cantidades de mano de obra y capital que se deben utilizar para producir una determinada cantidad de producción lo más barata posible.

Por supuesto, respondemos a esta pregunta configurando y resolviendo un problema de optimización; luego hacemos estática comparada. Debido a que hay una restricción (debemos producir la q dada), usaremos el método Lagrangean.

Configuración del problema

El enfoque económico organiza los problemas de optimización respondiendo a tres preguntas:

1. ¿Cuál es el objetivo?

2. ¿Cuáles son las variables de elección?

3. ¿Cuáles son las variables dadas?

El objetivo es minimizar el costo total, TC, que es simplemente la suma del monto pagado a los trabajadores, wL, y el monto gastado en el alquiler de máquinas, Rk.

Las variables endógenas son L y K. La mano de obra se mide en horas y el capital es el número de máquinas. La firma puede decidir producir la producción dada siendo intensiva en mano de obra (usando mucha mano de obra y poco capital), o cantidades aproximadamente iguales de ambos, o alquilando mucha maquinaria y usando poca mano de obra.

Las variables exógenas son los precios de entrada, la tasa salarial (w) y el precio de alquiler del capital (r). La tasa salarial, o salario para abreviar, se mide en $/hora y el precio de renta del capital es de $/máquina. Suponemos que la firma es un tomador de precios en los mercados de mano de obra y capital por lo que puede rentar tanto L y K como quiera a las w y r dadas. La cantidad a producir, q, es también una variable exógena en este problema. No estamos considerando cuánto se debe producir, sino cuál es la mejor manera de producir cualquier cantidad dada de producción. Por último, también se da la tecnología de la firma\(f(L, K)\), la función de producción.

Debido a que la empresa tiene que producir una cantidad determinada de producción, sabemos que este es un problema de optimización restringido. Nuestro trabajo en la Teoría del Comportamiento del Consumidor nos ha hecho expertos en resolver este tipo de problemas. Como verás, el análisis es similar, pero hay algunas diferencias llamativas.

Una cosa que no cambia es nuestro marco. Primero exploramos la restricción para determinar nuestras opciones, luego nos enfocamos en el objetivo (minimizar la TC) y, finalmente, combinaremos las dos para encontrar la solución óptima inicial.

La restricción

El menú de opciones disponibles para la firma viene dado por el isoquant. Sirve como restricción porque la firma es libre de elegir L y K con la condición de que debe producir el nivel de salida asignado. Matemáticamente, la ecuación para la restricción es simplemente la función de producción,\(q = f(L, K)\).

PASO Abra el libro de Excel InputCostMin.xls, lea la hoja de introducción, luego vaya a la hoja Isoquant para ver el isocuante que se muestra en la Figura 11.1.

Figura 11.1: Un isocuante de una función de producción de Cobb-Douglas.

Fuente: InputCostMin.xls! Isocuante.

Al igual que la restricción presupuestal en la Teoría del Comportamiento del Consumidor nos da posibilidades de consumo, el isoquant le da a la firma sus opciones de insumos factibles Se descartan todas las combinaciones abajo e izquierda del isocuante. Por ejemplo, no hay forma de producir 100 unidades de salida, manteniendo constante la calidad y todo lo demás, con la combinación L, K de 100,20. La tecnología simplemente no es avanzada ni lo suficientemente potente como para hacer 100 unidades de salida con 100 horas de trabajo y 20 máquinas.

Los puntos anteriores y a la derecha del isocuante son factibles, pero claramente son derrochadores. Es decir, la firma podría producir 100 unidades de producción con una combinación L, K de 250,50, pero el isocuante le dice a la firma que no necesita tanta mano de obra y capital para hacer 100 unidades. A 250,50, podría viajar recto hacia abajo a K = 10 y aún así producir q = 100 o recto a la izquierda (en la línea horizontal en K = 50) hasta que golpee el isoquante y use mucha menos mano de obra. La firma también podría viajar en diagonal, dirección suroeste hasta llegar al isocuante para economizar en ambos insumos.

Se dice que los puntos fuera del isoquante hacia el noreste (como 250,50) son técnicamente ineficientes. La parte ineficiente nos dice que la firma no está minimizando su costo total en ese momento; técnico describe el hecho de que la firma no está organizando sus insumos para maximizar la producción. Es decir, la firma no está resolviendo correctamente el problema de optimización de ingeniería que representa la función de producción. Hacer 100 unidades de salida con 250 horas de mano de obra y 50 máquinas significa que no estás sacando el máximo provecho de tu mano de obra y capital. Los economistas llaman a esta situación técnicamente ineficiente.

Dado que la firma no puede elegir una combinación por debajo del isocuante y es derrochador elegir una combinación por encima del isocuante, sabemos que la respuesta tiene que estar en el isoquante.

PASO Usa la barra de desplazamiento junto a la celda B11 para ver las mezclas de entrada que la firma podría elegir. A medida que cambia la celda B11, la celda de abajo también cambia. Tiene una fórmula que calcula la cantidad de K necesaria para producir la salida requerida cuando se elige un valor para L.

La idea es bastante clara: La firma rodará alrededor del isoquante en busca de la mejor combinación. Rodar es una buena elección de palabras e imagen para recordarla firma es libre de elegir un punto alto hacia arriba o rodar hacia abajo hacia la parte inferior derecha. Debido a que no tenemos los precios de los insumos, no podemos encontrar la solución óptima solo con el isoquant.

PASO Cambiar las variables exógenas para ver cómo se ve afectado el isocuante. Los aumentos en A, c y d tiran el isoquante hacia abajo. Eso tiene sentido dado que estos choques son todos potenciadores de la productividad y la firma necesitará menos L y K para hacer el q = 100 dado.

Bajar q tiene el mismo efecto, pero esto no es un choque de productividad. Simplemente le estás diciendo a la firma que no tiene que producir tanto como antes así tiene sentido que pueda usar menos mano de obra y capital.

Observe cómo la restricción para este problema de minimización de costos de entrada es una curva, no una línea como lo fue para el problema de maximización de servicios públicos. Matemáticamente, eso no importa mucho, pero impactará en la gráfica que dibujemos para mostrar la solución inicial.

Gol

Con la restricción en la mano, estamos listos para modelar la meta. En este problema, el objetivo está representado por una serie de líneas de isocosto (igual costo).

El costo total es\(TC = wL+ rK\). Si resolvemos esta ecuación para K (para poder graficarla en el espacio L - K), obtenemos la ecuación de una línea:\[TC = wL + rK\]\[rK = TC - wL\]\[K = \frac{TC}{r} - \frac{w}{r}L\] La intercepción K (o eje y) es\(\frac{TC}{r}\) y la pendiente es\(- \frac{w}{r}\).

Los isocostos son un poco difíciles al principio porque estás acostumbrado a ver una restricción lineal y un conjunto de curvas de indiferencia. La minimización de costos de entrada tiene una restricción curva y un conjunto de isocostos lineales. En la ecuación de la línea anterior, TC puede tomar cualquier valor. Por lo tanto, hay un isocosto por\(TC=\$500\) y otro para\(TC=\$500.01\) y un isocosto por cada monto en dólares. Cada punto L, K está en un isocosto y los puntos L, K que tienen el mismo TC están en el mismo isocosto.

PASO Proceder a la hoja de Isocosto para ver cómo se utilizan las líneas de isocosto para encontrar la solución óptima.

Cada punto de una línea de isocosto en particular tiene exactamente el mismo costo total. Entonces, el punto en la Figura 11.2 (y en tu pantalla) tiene un costo de $500 (desde 2 x 190 + 3 x 40 = 500).

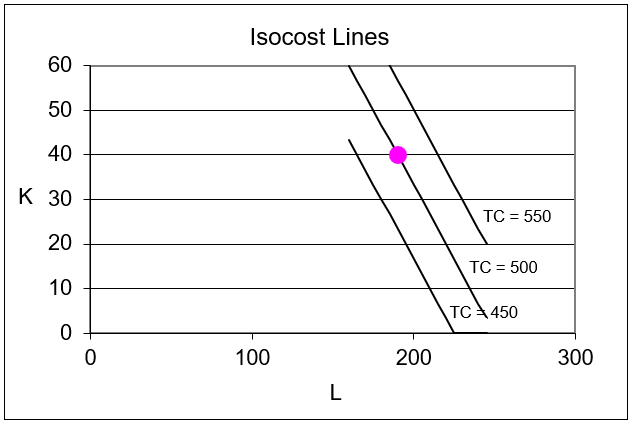
Figura 11.2: Tres líneas representativas de isocosto.

Fuente: InputCostMin.xls! Isocosto.

PASO Haga clic en el para ver cómo se representa el objetivo de minimización de costos de la firma en esta gráfica.

La firma puede pasar a un nuevo punto eligiendo una combinación diferente de L y K. Si el nuevo punto tiene el mismo TC de $500 que el punto inicial, entonces estará en el mismo isocosto de $500.

PASO Incrementa L en 30 y disminuye K en 20 por lo que estarás en otro punto de la misma línea de isocosto de $500.

Ahora ya sabes que todos los puntos en la línea TC = $500 de isocosto comparten el mismo costo total de $500. También es obvio que la pendiente de cada línea de isocosto es\(- \frac{2}{3}\) desde\(w=2\) y\(r=3\).

Debido a que la firma puede elegir la mezcla de entrada, puede elegir cualquier combinación de L y K, siempre que la combinación elegida pueda producir la cantidad dada de salida. La firma quiere contratar el menor número de insumos que pueda (para ahorrar en costos), pero tiene que cumplir con el objetivo de producción. ¿Cómo puede resolver este problema?

La solución óptima inicial

Tenemos la restricción (el isocuante) y el objetivo (llegar al isocosto más bajo posible), así que ahora combinamos los dos para encontrar la solución óptima.

PASO Proceda a la hoja OptimalChoice.

La posición inicial muestra una combinación L, K que cuesta 482.81 dólares. Puede confirmar este número tanto en la celda B7 como en el gráfico (la etiqueta del medio para la línea media).

La idea es estar en la línea de isocosto más baja (es decir, la que tiene la menor intercepción) que solo está tocando el isocuante porque eso significa que la firma estará minimizando el costo total de producir el nivel de producción dado.

Claramente, la posición inicial no es óptima. Se puede ver que el isocosto se está cruzando con el isoquante. Esta información también es revelada por la pendiente y la información TRS debajo del gráfico. El TRS, que es la pendiente del isocuante en un punto, es mayor (en valor absoluto) que la pendiente de la línea de isocosto en ese punto.

En la posición de apertura, se dice que la firma sufre de ineficiencia asignadora porque está en el isocuante, pero no logra elegir la mezcla de insumos minimizando costos. Debido a que está en el isoquant, sabemos que no es técnicamente ineficientees usar la combinación de apertura de L y K para obtener la máxima salida. El problema es que está utilizando la combinación incorrecta de entradas en el sentido de que hay una manera más barata de producir la salida dada.

Sabemos que hay dos formas de resolver problemas de optimización: analítica y numéricamente. Debido a que tenemos Excel y el problema implementado en la hoja, comenzamos con el enfoque numérico.

PASO Ejecutar Solver. La solución óptima se representa mediante el gráfico canónico que se muestra en la Figura 11.3.

La respuesta de Solver, que es correcta, hace que la firma elija una combinación L, K cuyo isocosto apenas toca el isocuante. No hay una combinación más barata que pueda producir 100 unidades con la tecnología existente (dada por la función de producción). Si la firma iba a un isocosto que era un centavo menor, no podría rentar suficientes L y K para hacer 100 unidades de producción.

Figura 11.3: La solución óptima inicial.

Fuente: InputCostMin.xls! OptimalChoice, después de ejecutar Solver.

Podemos confirmar el resultado de Solver aplicando el método Lagrangean para resolver este problema de optimización restringida.

Comenzamos por anotar el problema, utilizando los valores de los parámetros de la hoja OptimalChoice. \[\begin{gathered} %star suppresses line # \min\limits_{L,K}TC=2L+3K\\ \textrm{s.t. } 100 = L^{0.75}K^{0.2}\end{gathered}\]El primer paso es reescribir la restricción para que sea igual a cero. \[100 - L^{0.75}K^{0.2}=0\]El segundo paso es formar el Lagrangean agregando lambda,\(\lambda\), veces la restricción reescrita a la función objetiva original. Utilizamos una L extra grande para la función lagrangea que no está en absoluto relacionada con la L para el trabajo de parto. \[\begin{gathered} %star suppresses line # \min\limits_{L,K, \lambda}{\large\textit{L}}=2L+3K + \lambda (100- L^{0.75}K^{0.2})\end{gathered}\]El tercer paso para encontrar la solución óptima es tomar la derivada del Lagrangean con respecto a cada variable endógena y establecer cada derivada a cero (dándonos las condiciones de primer orden).

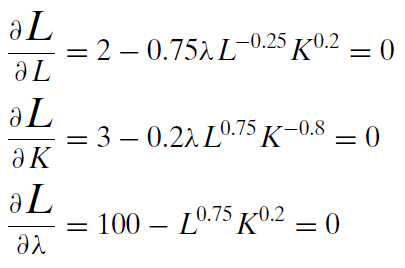
El cuarto, y último, paso es resolver este sistema de ecuaciones para\(L\mbox{*}\),\(K\mbox{*}\), y\(\lambda \mbox{*}\). El sistema de tres ecuaciones contiene la respuesta, es decir, los valores de L y K que minimizan la TC. Nuestra tarea es utilizar las ecuaciones para encontrar estos valores que satisfagan las tres ecuaciones.

Hay muchas formas de resolver el sistema, pero usaremos el mismo enfoque que usamos en la Teoría del Comportamiento del Consumidor. Reduciremos el sistema de 3 a 2 a 1 ecuación y desconocido.

Movemos los términos con lambda en las dos primeras ecuaciones hacia el lado derecho y luego dividimos la primera ecuación por la segunda. La función de producción Cobb-Douglas es fácil de trabajar porque los exponentes de L y K suman -1 y 1, respectivamente, cuando se aplica la\(\frac{x^a}{x^b}=x^{a-b}\) regla.

Como puedes ver arriba, esta estrategia cancela las lambdas y da una expresión para\(L = f (K)\), lo que, en conjunto con la condición de tercer primer orden, reduce el sistema a dos ecuaciones con dos incógnitas. \[\begin{gathered} %star suppresses line # L=5.625K \\ 100- L^{0.75}K^{0.2}\end{gathered}\]Sustituimos la expresión de L en la restricción (la condición de tercer orden de primer orden) y resolvemos para\(K\mbox{*}\).

Entonces, sustituyendo de\(K\mbox{*}\) nuevo en la expresión por\(L = f (K)\), obtenemos\(L\mbox{*}\). \[\begin{gathered} %star suppresses line # L=5.625K \\ L=5.625[32.588] \\ L\mbox{*}=183.31\end{gathered}\]Sustituyendo\(L\mbox{*}\) y\(K\mbox{*}\) en la función objetivo original, podemos calcular el costo mínimo de producir 100 unidades. \[\begin{gathered} %star suppresses line # TC = 2L + 3K \\ TC = 2[183.1]+3[32.588] \\ TC\mbox{*}=\$464.38\end{gathered}\]La solución analítica concuerda con la respuesta de Solver.

El trabajo que hicimos al dividir la primera ecuación por la segunda produce una condición equimarginal que es similar a la\(\frac{p_1}{p_2}\) regla MRS = de maximización de utilidad restringida. En la solución óptima, tenemos\[\frac{2}{3}=\frac{3.75K}{L}\] El lado izquierdo es la relación precio de entrada y el lado derecho es el TRS. Así, en la solución óptima sabemos que la relación de precio de entrada debe ser igual al TRS. Esta es una declaración matemática de la tangencia que vemos en la Figura 11.3.

Si no se cumple esta condición equimarginal, pero la firma está en el isoquante (es decir, es técnicamente eficiente), entonces tenemos ineficiencia asignadora. Si\(|TRS| > \frac{w}{r}\), entonces el isocosto está cortando el isoquant y la firma puede reducir los costos totales al enrollar el isoquant. Lo contrario, por supuesto, aplica si\(|TRS| < \frac{w}{r}\).

PASO Si aún no lo ha hecho, haga doble clic dentro de la caja alrededor de la celda J25 y use la barra de desplazamiento para mostrar cómo la gráfica de isocosto e isocuante coincide con la condición TRS =\(\frac{w}{r}\) equimarginal.

Comparando Consumidor y Firme

La Figura 11.3 tiene un parecido llamativo con la gráfica canónica utilizada en la Teoría del Comportamiento del Consumidor y el trabajo analítico también contiene fuertes similitudes, pero existen algunas diferencias críticas entre los problemas de optimización del consumidor y la empresa. La Figura 11.4 presenta una comparación lado a lado para resaltar los contrastes entre ellos.

Figura 11.4: Comparación de problemas de optimización del consumidor y de la empresa.

Tiene sentido utilizar los conocimientos y habilidades aprendidas de la Teoría del Comportamiento del Consumidor, pero no caer en una falsa sensación de seguridad. El problema de minimización de costos de entrada tiene sus propias características y terminología.

La minimización de costos es uno de tres problemas

La Teoría de la Firma es en realidad un conjunto de tres problemas de optimización interrelacionados. La solución inicial al problema de minimización de costos de la empresa enfoca la atención en la combinación más barata de insumos para producir un nivel de producción dado.

Podemos aplicar las mismas técnicas que utilizamos para resolver el problema de maximización de la utilidad del consumidor. La gráfica canónica es similar a la gráfica estándar de la Teoría del Comportamiento del Consumidor, pero como muestra la Figura 11.4, existen diferencias sustanciales entre la maximización de la utilidad y la minimización de costos.

Una similitud importante es el uso continuado de la comparación de una relación precio con la pendiente de una curva para determinar si se ha encontrado la solución óptima. En el caso del problema de minimización de costos restringidos, la firma elegirá esa combinación de insumos donde TRS =\(\frac{w}{r}\). Si no se cumple esta condición, la dirección de la desigualdad (> o <) nos indica en qué dirección debe moverse la firma para encontrar el costo total mínimo.

Ahora que entendemos el problema de minimización de costos de la firma y hemos encontrado la solución inicial, estamos preparados para dar el siguiente pasoanálisis estadístico comparativo. El enfoque económico es implacable y monótono. Aplicamos el mismo marco a cada problema. A través de la práctica y la repetición, aprenderás a pensar como economista.

Ejercicios

1. La hoja de preguntas y respuestas le pide cambiar r a 30 y usar Solver para encontrar la solución inicial. Encuentre la solución inicial a este mismo problema a través de métodos analíticos y compare los dos resultados. ¿Son lo mismo? Muestre su trabajo.

2. La función de producción de proporciones fijas,\(q = min\{\alpha L, \beta K\}\) es análoga a la forma funcional perfecta complementa la utilidad. Supongamos\(\alpha = \beta = 1\), w = 10, r = 50 y q = 100. Encontrar\(L\mbox{*}\),\(K\mbox{*}\), y\(TC\mbox{*}\). Muestre su trabajo. Utilice las Herramientas de Dibujo de Word para dibujar una gráfica de la solución óptima.

3. Dada la función de producción cuasilineal\(q = \sqrt{L}+K\), y los precios de entrada r = 2, y w = 5, encuentran la manera más barata de producir 1000 unidades de producción. Usa métodos analíticos y muestra tu trabajo.

4. Configura el problema en la pregunta 3 en Excel y usa Solver para encontrar la solución óptima. Tome una captura de pantalla de la solución en su hoja de cálculo y péguela en un documento de Word.

5. ¿Pueden los isocuantes cruzarse? Explique por qué o por qué no.

Referencias

El epígrafe es de la página 1044 de Historia del análisis económico de Joseph Schumpeter (publicada en 1954, poco después de su muerte). Este clásico traza la historia intelectual de la economía desde Aristóteles hasta el siglo XX. Schumpeter revisa las teorías y visiones de gigantes como Adam Smith y Karl Marx, pero también de un increíble número de filósofos y economistas que no te serán familiares.

Ragnar Frisch, al que Schumpeter le atribuye haber inventado el término isoquant, tenía una habilidad especial para inventar palabras, e.g., macroeconomía y econometría. Por suerte, la “flexibilidad de costos sustitutivos” no se dio cuenta. Noruego, Frisch formó parte de una tradición cuantitativa y empírica excepcionalmente fuerte en la economía escandinava que sigue viva hasta nuestros días.