11.4: Curvas de Costo

En el siguiente capítulo, trabajaremos en el segundo problema de optimización de la firma: maximizar las ganancias eligiendo la cantidad de producción a producir. Debido a que las ganancias son ingresos menos costos, la función de costo juega un papel importante en el problema de maximización de ganancias de la empresa.

Esta sección está dedicada a la terminología de las curvas de costo y a una exploración de sus propiedades geométricas. Derivado de la función de costo, se utilizan una variedad de curvas de costos para resolver y mostrar el problema de maximización de ganancias de la empresa. Esta sección los define y deriva.

Una idea básica que es fácil de olvidar es que hay muchas formas de funciones de costo. Nuestro trabajo en la derivación de la función de costo utilizó una función de producción de Cobb-Douglas y eso da lugar a una función de costo particularmente conformada. Una función de producción diferente daría una función de costo diferente. Una idea clave es que\(q=f(L,K)\) determina la forma de\(TC \mbox{*}=f(q)\).

Nombres y acrónimos

Sabes que si hacemos un seguimiento\(TC \mbox{*}\), costo total mínimo, en función de q, derivamos la función de costo. Ya que usaremos otras medidas de costos, para evitar confusiones, nos referimos a la función de costo como la función de costo total (TC). La función costo total tiene unidades de dólares ($) en el eje y. Podemos dividir los costos totales en dos partes, costos variables totales, TVC, y costos fijos totales, TFC. \[TC(q) = TVC(q) + TFC\]Si la firma se encuentra en el corto plazo, tiene al menos un factor fijo de producción (generalmente K) y los costos fijos totales son el valor en dólares gastado en los insumos fijos (RK). Observe que los costos fijos totales no varían con la salida. TFC es una constante y no cambia a medida que cambia la salida por lo que no hay “(q)” en la función TFC como hay en TVC y TC.

Los costos variables totales son los costos de los factores que la firma es libre de ajustar o variar (de ahí el nombre “costos variables”), generalmente L. A medida que aumenta la producción, las empresas necesitan más insumos para producir la mayor producción, por lo que aumentan los costos variables totales.

A la larga, definido como un horizonte de planeación en el que no hay factores fijos, no hay costos fijos (TFC = 0) y, por lo tanto,\(TC(q) = TVC(q)\). En otras palabras, las funciones de costo total y costo variable total son idénticas.

Además de los costos totales, la firma tiene costos promedio, o por unidad, asociados a cada nivel de producción. El costo total promedio, ATC (también conocido como AC), es el costo total dividido por el nivel de salida. \[ATC(q)=\frac{TC(q)}{q}\]El costo variable promedio, AVC, es el costo variable total dividido por la producción. \[AVC(q)=\frac{TVC(q)}{q}\]El costo fijo promedio, AFC, es el costo fijo total dividido por la producción. \[AFC(q)=\frac{TFC(q)}{q}\]Observe que AFC (q) es una función de q aunque TFC no lo sea porque AFC sea TFC dividido por q. Dado que el numerador es una constante, AFC (q) es una hipérbola rectangular (\(y = c/x\)) y se garantiza que caiga a medida que q suba. Esto se puede confirmar con un simple ejemplo. Decir TFC = $100. Para q muy pequeños, como 0.0001, AFC es extremadamente grande. Pero AFC cae muy rápido ya que q sube de cero (y AFC no está definido en q = 0). At\(q =1\), AFC es de $100, a q = 2, AFC es de $50, y así sucesivamente. Cuanto mayor sea el valor de q, más cerca se acerca el AFC a cero (es decir, se acerca al eje x).

Es fácil demostrar que el costo total promedio debe ser igual a la suma de la variable promedio y los costos fijos promedio: A menudo\[TC(q) = TVC(q) + TFC\]\[\frac{TC(q)}{q} = \frac{TVC(q)}{q} + \frac{TFC}{q}\]\[ATC(q) = AVC(q) + AFC(q)\] omitimos AFC (q) de la visualización gráfica de la estructura de costos de la firma (ver Figura 11.14) porque sabemos eso\(AFC(q) = ATC(q) - AVC(q)\). Por lo tanto, el costo fijo promedio se puede determinar fácilmente simplemente midiendo la distancia vertical entre ATC y AVC a una q dada.

Los hechos que\(AFC(q) = ATC(q) - AVC(q)\) y AFC va a cero a medida que q sube significa que AVC debe acercarse a ATC a medida que q sube. Siempre dibuja CVA acercándose al ATC a medida que q aumenta más allá del CVA mínimo. La Figura 11.14 obedece a esta condición.

A diferencia de las curvas totales, que comparten el mismo eje y unidades de dólares, los costos promedio son una tasa, dólares por unidad de producción. No se pueden trazar curvas de costo total y promedio en la misma gráfica porque los ejes y son diferentes.

Otro concepto de costo que obtenemos de la función de costo total es el costo marginal (MC). Al igual que los costos promedio, MC es una tarifa y viene en $/unidad. El costo marginal a menudo se grafica junto con las curvas promedio (como se muestra en la Figura 11.14).

Medias marginales adicionales en economía. El costo marginal le indica el costo adicional de producir más producción. Si el cambio en la salida es discreto, entonces estamos midiendo el costo marginal de un punto a otro en la curva de costo y la ecuación se ve así:\[MC(q)=\frac{\Delta TC(q)}{\Delta q}\] Si, por otro lado, tratamos el cambio en la salida como infinitesimalmente pequeño, entonces usamos la derivada y tenemos:\[MC(q)=\frac{dTC(q)}{dq}\] Porque TFC no varía con q, costo marginal también se puede encontrar tomando el derivado de TVC (q) con respecto a q.

El costo promedio y el costo marginal se utilizan para referirse a funciones completas (ver Figura 11.14), pero también a valores específicos. Por ejemplo, si ATC = $10/unidad y MC = $3/unidad at\(q=5\), esto significa que cuesta $10 por unidad hacer las cinco unidades y, así, la firma tuvo $50 de costos totales para hacer cinco unidades. El MC nos dice que la ^5ª unidad cuesta $3 adicionales por lo que el costo total pasó de $47 por 4 unidades a $50 por 5 unidades.

La geometría de las curvas de costo

Las curvas promedio y marginales están conectadas entre sí y deben dibujarse de acuerdo a estrictos requisitos. Siempre que una curva marginal esté por encima de una curva promedio, la curva promedio debe estar subiendo. Por el contrario, siempre que un marginal esté por debajo de un promedio, el promedio debe estar bajando.

Por ejemplo, considere la puntuación promedio en un examen. Después de calificar a los 10 primeros alumnos, hay una puntuación promedio. Ahora se califica al estudiante número 11. Supongamos que obtiene una puntuación por encima de la media. La suya es la puntuación marginal y sabemos que está por encima de la media por lo que tiene que sacar la media hacia arriba. Supongamos que al siguiente alumno le fue mal. Su puntaje marginal está por debajo de la media y tira el promedio hacia abajo. Entonces, sabemos que siempre que una puntuación marginal esté por debajo de la media, la media debe estar bajando y siempre que una puntuación marginal esté por encima de la media, la media debe estar subiendo. La única vez que el promedio permanece igual es cuando el puntaje marginal es exactamente igual al puntaje promedio.

Esta relación entre el promedio y el marginal significa que la curva de costo marginal debe intersectar la variable promedio y las curvas de costo total promedio en sus respectivos mínimos, como se muestra en la Figura 11.14. De q = 0 a la intersección de MC con ATC, MC está por debajo del ATC y el ATC cae. A la derecha de la intersección de MC con ATC, MC se encuentra por encima del ATC por lo que se levanta el ATC. Las curvas MC y AVC comparten la misma relación.

Figura 11.14: Relaciones marginales y medias.

La Figura 11.14 también muestra una propiedad que se destacó anteriormente: La brecha entre ATC y AVC debe caer a medida que q sube.

Comprenderás mejor estas ideas abstractas explorando ejemplos concretos. Se examinarán tres formas funcionales de costo:

1. Curvas de Costos Cobb-Douglas

2. Curvas de Costo Canónico

3. Curvas de Costo Cuadráticas

En lugar de memorizar hechos o puntos específicos, busque el patrón y las conexiones repetidas. Centrarse en la relación entre las curvas totales y medias y marginales.

PASO Abra el libro de Excel CostCurves.xls y lea la hoja de introducción, luego vaya a la hoja de CobbDouglas para ver el primer ejemplo.

1. Curvas de Costos Cobb-Douglas

La hoja CobbDouglas es la hoja CostFn del libro DerivingCostFunction.xls con las curvas ATC y MC trazadas debajo de la curva TC. La columna I tiene una fórmula para la curva TC usando\(L \mbox{*}\) y\(K \mbox{*}\), a partir de la cual podemos calcular ATC y MC en las columnas J y K. Pulsar en una celda MC, por ejemplo, la celda K4, para ver que la fórmula de la celda es en realidad para \(\lambda \mbox{*}\). Estamos usando el atajo que\(\lambda \mbox{*}\) = MC.

Con L y K ambos endógenos, no hay factores fijos de producción. Esto significa que estamos a la larga y no hay costos fijos. Así, TC = TVC y ATC = AVC.

Es inmediatamente obvio que las curvas marginal y promedio no se parecen en absoluto a la familia convencional de curvas de costo como se muestra en la Figura 11.14. De hecho, una función de producción de Cobb-Douglas no puede dar curvas de costo promedio y marginal en forma de U como en la Figura 11.14.

Recuerde que existen muchas formas funcionales para las curvas de costo (total, promedio y marginal) y la forma depende de la función de producción. Es decir, la función de producción se expresa en la estructura de costos de una empresa.

PASO Establezca el exponente sobre el capital, d, en 2 para replicar Figura 11.15.

Figura 11.15: El costo total cambia a la baja cuando aumenta la productividad laboral.

Fuente: CostCurves.xls! CostFn, después de establecer d = 2.

Debido a que el costo promedio está cayendo a medida que q sube en la Figura 11.15 (y la pantalla de su computadora), significa que el costo total está aumentando menos que linealmente a medida que aumenta la salida. El gráfico de costo total en tu pantalla confirma que este es el caso. Cuesta 33 dólares hacer 200 unidades, pero sólo 43 dólares para hacer 400 unidades. Doble salida nuevamente a 800. ¿Cuánto cuesta? La celda I9 te dice, $55. Esto es desconcertante. Si los precios de los insumos se mantienen constantes, ¿cómo podemos duplicar la producción y no al menos duplicar los costos?

La respuesta está en la función de producción. Cambiaste el exponente sobre el capital, d, de 0.2 a 2. Ahora la suma de los exponentes,\(c + d\), es mayor que 1. Para la función de producción Cobb-Douglas, esto significa que estamos operando bajo rendimientos crecientes a escala. Esto quiere decir que si duplicamos las entradas, obtenemos más del doble de la salida. O, dicho de otra manera, podemos duplicar la salida usando menos del doble de las entradas.

Esta firma puede hacer 400 unidades más económicas por unidad que 200 unidades. Puede hacer que 800 unidades sean aún más baratas por unidad porque está aprovechando los crecientes rendimientos a escala.

El aumento de los rendimientos es un gran problema a los ojos de algunos economistas porque llevan a una paradoja: Una empresa debería hacer todo el producto. Hay situaciones en las que los rendimientos crecientes parecen estar justificados, como el caso de los monopolios naturales, en los que una sola empresa proporciona la producción para toda una industria debido a que la función de producción exhibe rendimientos crecientes a escala. Los ejemplos clásicos son empresas de servicios públicos, por ejemplo, compañías eléctricas, de agua y de gas natural. A menudo, estas firmas están nacionalizadas o fuertemente reguladas.

Podemos enfatizar la conexión crucial entre la función de producción y la función de costo a través del mapa isocuante.

PASO Desplázate hacia abajo hasta la fila 100 más o menos en la hoja de CobbDouglas.

Los tres isocuantes se basan en una función de producción Cobb-Douglas con valores de parámetros desde la parte superior de la hoja, excepto para d, que se puede manipular desde los botones de opción Set d (arriba del gráfico). Los tres puntos rojos son las combinaciones de entrada minimizando costos para tres niveles de salida diferentes: 100, 120 y 140.

Encima de la gráfica, se muestra el valor de la suma de los exponentes, inicialmente 0.95. Se muestra una descripción de la forma de la función de costo total, que depende del valor de c + d, y se muestra una pequeña imagen de esa forma. La Figura 11.16 tiene la pantalla inicial.

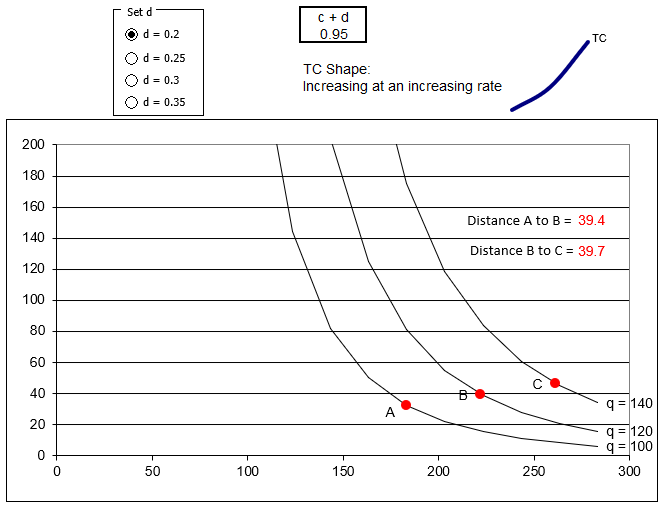
Figura 11.16: Los isocuantes determinan la forma de la función de costo.

Fuente: CostCurves.xls! CobbDouglas.

El espaciamiento entre los puntos es crítico. La distancia de A a B es un poco menor que la de B a C. Esto significa que a medida que la salida se incrementa de 120 a 140, la firma necesita un aumento mayor en las entradas que cuando q subió de 100 a 120.

A medida que la producción continúa aumentando en 20 unidades, el siguiente isocuante que tenemos que alcanzar es cada vez más lejos, requiriendo progresivamente más insumos y costos progresivamente más altos. Es por ello que TC está aumentando a un ritmo creciente.

PASO Haga clic en la opción d = 0.25.

Los isocuantes se desplazan porque se necesitan menos entradas para hacer los tres niveles de salida representados. La distancia entre los isocuantes ha disminuido y la TC es lineal. Lo más importante es que la distancia entre los puntos es idéntica.

Con\(c + d = 1\), el espaciamiento de los isocuantes es constante. A medida que q aumenta en 20, el siguiente isocuante está a la misma distancia y la firma aumenta su uso de insumos y costos en una cantidad constante. Es por ello que la función TC es una línea, aumentando a un ritmo constante.

PASO Haga clic en la opción d = 0.3.

Una vez más, el gráfico se actualiza y los isocuantes se desplazan. Ahora la distancia entre los isocuantes está disminuyendo. A medida que q sube, los isocuantes se acercan y la función de costo total aumenta a una tasa decreciente.

PASO Haga clic en la opción d = 0.35.

Esto produce rendimientos crecientes aún más fuertes y una función TC que se dobla más rápido que d = 0.3.

El punto fundamental es que la distancia entre los isocuantes refleja la función de producción. Hay tres casos:

1. Si la distancia va aumentando a medida que se aplican aumentos constantes en la cantidad, la función de costo total aumentará a una tasa creciente.

2. Si la distancia permanece constante, la función de costo será lineal.

3. Si la distancia disminuye a medida que aumenta la producción, la firma tiene costos que suben a un ritmo decreciente.

Esto es válido para todas las funciones de producción y, en el caso de Cobb-Douglas, es fácil ver lo que está pasando porque el valor de c + d revela inmediatamente los retornos a escala y el espaciamiento entre los isoquantes.

Pero la ventaja de Cobb-Douglas en mostrar fácilmente los tres casos (dependiendo del valor de C + d) significa que no puede hacer los tres casos a la vez. Una función de producción Cobb-Douglas puede generar una función TC que está aumentando a una tasa creciente o constante o decreciente, pero no a los tres.

La forma de la función de costo depende de la tecnología de producción. Repetidamente recorre los botones de radio, vigilando las isocuantes, la distancia entre los puntos y la función de costo total resultante. Su tarea es comprender y cimentar la relación entre las funciones de producción y costo.

Un acordeón es una buena metáfora de lo que está pasando. Al arrugarse, los isocuantes están siendo apretados entre sí, lo que da rendimientos crecientes a escala y TC aumentando a un ritmo decreciente. Cuando el acordeón se expande y los isocuantes están muy separados, tenemos rendimientos decrecientes a escala y TC subiendo a un ritmo creciente.

No se confunda. La razón por la que aumentar (disminuir) los retornos a la escala lleva a que la TC suba a una tasa decreciente (creciente) (son opuestos) es que la productividad (retornos a escala) y los costos son opuestos. El aumento de la productividad permite aumentos más lentos en los costos de producción. La producción que aumenta a un ritmo creciente y los costos que aumentan a un ritmo decreciente son dos caras de una misma moneda.

2. Curvas de Costo Canónico

PASO Proceder a la lámina cúbica.

Esta hoja muestra la estructura de costos canónicos, es decir, la función de costo más utilizada. Produce la familia familiar en forma de U de costos promedio y marginales (que Cobb-Douglas no puede).

El gráfico de curvas de costo canónico puede ser generado por una función de costo con una forma funcional polinómica cúbica. \[TC(q) = aq^3 + b q^2 + c q + d\]El coeficiente d (que no debe confundirse con el exponente d en la función de producción de Cobb-Douglas) representa el costo fijo. Si\(d > 0\), entonces hay costos fijos y sabemos que la firma está en el corto plazo.

Una vez que tenemos la función de costo, la curva superior en la gráfica superior en la hoja cúbica, podemos aplicar las definiciones de costos (desde el inicio de esta sección) para obtener todas las demás curvas de costo. Las otras curvas totales son:\[TVC(q) = aq^3 + b q^2 + c q\]\[TFC = d\]

PASO Haga clic en cada una de las tres curvas en la gráfica superior de la hoja Cúbica para ver los datos que se están trazando.

Ahora dirija su atención a la gráfica inferior. Las curvas en la gráfica inferior se derivan todas de la gráfica superior. Observe que la etiqueta del eje y es diferente, los totales en la parte superior tienen unidades de $, mientras que las curvas promedio y marginales tienen una escala y de $/unidad (de salida).

PASO Haga clic en cada una de las tres curvas en la gráfica inferior para ver los datos que se están trazando.

Se ha aplicado formato personalizado a los números en las celdas de costo promedio y marginal para mostrar “$/unidad” en cada celda. Es fácil olvidar que “$” no son las unidades de las curvas de costo promedio y marginal.

Los costos variables promedio total y promedio son fáciles de calcular: simplemente divida el total por q. Puedes confirmar que la fórmula de la columna E hace exactamente esto. No hay ningún valor ATC\(q=0\) porque dividir por cero no está definido.

También podemos dividir la ecuación en sí por q para obtener un promedio. Esto se hace para CVA. La fórmula en la celda F2 es “= a_* (A6^2) + B_*a6 + c_” porque dividir\(TVC(q) = aq^3 + b q^2 + c q\) por q rinde\(= aq^2 + b q + c\). Observe que AVC para\(q=0\) sí existe.

El costo marginal es más difícil de entender que el costo promedio. El costo marginal se define como el costo adicional de producir más producción. “Más” puede ser una cantidad arbitraria, finita (como 1 unidad o 10 unidades) o un cambio infinitesimalmente pequeño en el número de unidades.

Si usamos una cantidad arbitraria y finita de incremento en q, entonces calculamos MC como\(\frac{\Delta TC}{\Delta q}\). También podemos calcular MC para un cambio infinitesimalmente pequeño, usando la derivada,\(\frac{dTC}{dq}\). Estos dos cómputos serán exactamente los mismos solo si MC es una línea.

Los dos enfoques se aplican en las columnas G y H. La derivada de TC con respecto a q es:\[TC(q) = aq^3 + b q^2 + c q + d\]\[\frac{dTC}{dq} = 3aq^2 + 2b q + c\]

Observe cómo aplicamos la regla derivada habitual, bajando el exponente y restando uno del exponente para cada término. El coeficiente d, TFC, desaparece porque no tiene q en él (o, si lo prefieres, piensa en d como\(dq^0\)). La expresión para MC se ingresa en la columna G.

La columna H tiene MC para un cambio de tamaño discreto. Se puede variar el tamaño del cambio en q ajustando el tamaño del paso en la celda B3.

PASO Haz que el tamaño del paso sea cada vez más pequeño. Prueba 0.1, 0.01 y 0.001.

A medida que se hace más pequeño el tamaño del paso, los valores en la columna H se acercan a los de la columna G. Esto, una vez más, demuestra el concepto de la derivada.

Otra forma de obtener la función de costo es usar el resultado ordenado del método Lagrangean. Simplemente podemos usar\(\lambda \mbox{*} = MC\) y tenemos la curva MC. No se requiere cambio de tamaño delta o derivado. Si lo que realmente queríamos era la función de costo total, entonces tendríamos que integrar la\(\lambda \mbox{*}\) función con respecto a q. La constante de integración es el costo fijo, que sería cero a la larga.

La familia de curvas de costo en las hojas Intro y Cúbico (y en la Figura 11.14) son las curvas de costo canónicas que se muestran en innumerables libros de texto de economía. Podría preguntarse, si no Cobb-Douglas, entonces ¿qué función de producción podría producir tal función de costo? Esa no es una pregunta fácil de responder. De hecho, la forma funcional de la tecnología que daría lugar a las curvas de costo canónico es bastante complicada y no vale la pena el esfuerzo de derivar minuciosamente las curvas habituales de costos promedio y marginales en forma de U a partir de los primeros principios.

Es suficiente saber que una función de producción subyace a la función TC polinómica y sus curvas de costo promedio y marginal en forma de U resultantes. También queremos tener en cuenta que si los precios de los insumos suben, las curvas de costos cambian hacia arriba y, si la tecnología mejora, bajan.

3. Curvas de Costo Cuadráticas

PASO Proceder a la hoja Cuadrática para ver un ejemplo final de curvas de costo.

De inmediato queda claro que la forma funcional cuadrática es un caso especial de la función de costo cúbico, con coeficientes a y c iguales a cero.

Mire la tabla superior y conecte las formas de las funciones TC, TVC y TFC a la forma funcional\(TC(q)=bq^2+d\). Dados los valores de coeficiente en la hoja, esto da\(TC(q)=q^2+1\),\(TVC(q)=q^2\), y\(TFC=1\).

El gráfico inferior no parece familiar, pero obedece a las definiciones de costo promedio y marginal explicadas anteriormente en esta sección. ATC se\(TC(q)\) divide por q:\(ATC(q)=q+\frac{1}{q}\). De igual manera, AVC es\(TVC(q)/q\), que es q (un rayo fuera del origen). MC es la derivada de TC con respecto a q, que es 2q.

Aunque no son las curvas habituales en forma de U, la curva MC (en realidad, MC es lineal) cruza AVC y ATC en sus mínimos. Cuando MC está por debajo de ATC, ATC está cayendo, pero más allá del punto en el que MC se cruza con ATC (en el ATC mínimo), MC está por encima de ATC y ATC está subiendo. A medida que q aumenta, CVA converge a ATC, lo que implica que AFC va a cero.

Las formas de las curvas de costo no son las curvas promedio y marginales habituales en forma de U, pero esta es otra de las muchas estructuras de costos posibles que podrían derivarse del problema de minimización de costos de entrada de una empresa.

El papel de las curvas de costos en la teoría de la firma

Las curvas de costo no son particularmente emocionantes, pero son una herramienta geométrica importante. Cuando se combina con la estructura de ingresos de una empresa, la familia de curvas de costos se utiliza para encontrar el nivel de producción maximizador de ganancias y las ganancias máximas.

Las curvas de costos pueden venir en muchas formas y formas, pero todas comparten la idea básica de que se derivan minimizando el costo total de producción, donde la producción es generada por la función de producción de la empresa. Diferentes funciones de producción dan lugar a diferentes funciones de costo.

La forma de la función de costo, que aumenta a una tasa creciente, constante o decreciente, está determinada por la función de producción. Con rendimientos crecientes a escala, por ejemplo, una empresa puede más que duplicar la salida cuando duplica su uso de entrada. Eso significa, en el lado del costo, que duplicar la producción será menos del doble del costo total. Los retornos a escala pueden ser manchados por el espaciado entre las isocuantes. Con rendimientos crecientes a escala, por ejemplo, las brechas entre las isocuantes se hacen más pequeñas a medida que aumenta la salida.

No importa la función de producción, siempre es cierto que para los niveles de producción en los que el costo marginal está por debajo de un costo promedio, el promedio debe estar cayendo y MC por encima de AVC o ATC significa que AVC o ATC está aumentando. También es cierto que, a corto plazo (cuando hay costos fijos), AVC se acerca a ATC a medida que aumenta la producción.

Por último, considere el mensaje que transmite la Figura 11.17. Las flechas muestran la progresiónpromedio y las curvas marginales provienen de la función de costo total, que proviene del problema de minimización de costos de entrada (con la función de producción expresada en los isocuantes).

Figura 11.17: Conexión de gráficos de costos.

Los economistas utilizan gráficas para comunicarse. Puede parecer que las gráficas son conjuradas de la nada, pero esto es falso. Todas las gráficas tienen una genealogía y una historia que contar. Cuando sabes de dónde vienen las gráficas, eso ayuda a leerlas correctamente.

Ejercicios

1. Una función de producción de Cobb-Douglas con rendimientos crecientes a escala produce una función de costo total que aumenta a una tasa decreciente. Utilice las herramientas de dibujo de Word para dibujar el mapa isocuante subyacente para dicha función de producción.

Una especificación comúnmente utilizada para las funciones de producción en el trabajo empírico es la forma funcional translog. Hay varias versiones. Cuando se aplica a la función de costo, obtiene un resultado como este:\[\ln TC\ = \alpha_0 + \alpha_1 \ln Q\ + \alpha_2 \ln w\ + \alpha_3 \ln r\ + \alpha_4 \ln Q\ \ln w\ + \alpha_5 \ln Q\ \ln r\ + \alpha_6 \ln w\ \ln r\ \] Observe que la función es una modificación de la versión de registro de una función Cobb-Douglas. Además de los términos logarítmicos individuales hay combinaciones de las tres variables, llamadas términos de interacción.

Haga clic en el botón en la parte inferior de la hoja de preguntas y respuestas en el libro CostCurves.xls para revelar una hoja con parámetros de función de costo de translog. Utilice esta hoja para responder a las siguientes preguntas.

1. Ingresa una fórmula en la celda B18 para el TC de producir 100 unidades de salida, dado el coeficiente alfa y los valores de precio de entrada en las celdas B5:B13. Rellene su fórmula y luego cree un gráfico de la función de costo total (con etiquetas de ejes apropiadas y un título). Copia y pega tu gráfico en un documento de Word.

   Consejos:\(TC = e \ln TC\ \) y el operador de exponenciación en Excel es EXP (). “=EXP (número)” en Excel devuelve e elevado a la potencia de ese número.

2. Calcular MC a través del cambio en la salida de 100 a 110 en la celda C19. Reporta tu resultado.

3. Calcular MC a través de la derivada a Q = 100 en la celda D18. Reporta tu resultado.

   Pista:\(\frac{d}{dx}(e^{f(x)})=e^{f(x)}\frac{d}{dx}(f(x))\)

4. Compara tus resultados para MC en las preguntas 3 y 4 ¿tus respuestas son iguales o diferentes? Explique.

Referencias

El epígrafe es de la página 218 de Alan Blinder, Elie Canetti, David Lebow y Jeremy Rudd, Preguntando por los precios: un nuevo enfoque para entender la adhesión de los precios (Fundación Russell Sage, 1998). Este libro reporta los resultados de entrevistas con más de 200 ejecutivos de negocios. Los autores explican que preguntar sobre el costo marginal de una empresa “resultó ser bastante complicado porque el término 'costo marginal' no está en el léxico de la mayoría de los empresarios; el concepto en sí puede que ni siquiera sea natural” (p. 216). La pregunta, por lo tanto, se formulaba en términos de “costos variables de producir unidades adicionales”.

Los resultados confirmaron lo que muchos que han intentado estimar curvas de costo saben: La familia canónica en forma de U de curvas de costo es una teoría agradable, pero no es común en el mundo real. De hecho, muchos líderes empresariales no tienen idea de qué es el costo marginal o cómo medirlo. No pierdas de vista, sin embargo, el propósito de la Teoría de la Firma. No está diseñado para describir de manera realista a una firma viva. La Teoría de la Firma es una abstracción severa con el objetivo principal de derivar una curva de oferta. El siguiente capítulo hace exactamente eso.