11.3: Derivar la función de costo

Hemos resuelto el problema de minimización de costos de entrada por lo que la siguiente tarea es el análisis estadístico comparativo. Nos enfocaremos en impactar q (la cantidad que la firma debe producir) y rastrear el costo total mínimo. La relación entre\(TC\mbox{*}\) y q se llama la función de costo.

La novedad aquí es que no nos interesa cómo varían los valores óptimos de las variables endógenas, L y K a medida que chocamos q. En cambio, nos enfocamos en la función objetiva, el costo total mínimo y cómo cambia a medida que cambia q.

Otro aspecto importante del análisis estadístico comparativo para el problema de minimización de costos de entrada es que, a diferencia de la utilidad en la Teoría del Comportamiento del Consumidor, el costo total se puede medir cardinalmente. Podemos comparar los costos totales de diferentes firmas y realizar aritmética sobre el costo total. Si el TC mínimo para\(q=10\) es de $40 y sube a $45 cuando\(q=11\), podemos decir que TC aumentó en $5. Debido a que TC es cardinal, podremos interpretar y utilizar el multiplicador lagrangeo.

Como es habitual, exploraremos ambas formas de hacer estáticas comparativas:

• Métodos numéricos usando una computadora: el Solver de Excel y el Asistente de Estadística Comparativa.

• Métodos analíticos mediante álgebra y cálculo: papel convencional y lápiz.

Métodos numéricos para derivar la función de costo

PASO Abra el libro de Excel DerivingCostFunction.xls, lea la hoja de introducción y continúe con la hoja OptimalChoice.

La organización es la misma que en el libro de trabajo InputCostMin.xls. La forma de minimizar costos de producir 100 unidades de producción es usar alrededor de 183.3 horas de mano de obra con 32.6 máquinas, lo que cuesta $464.38. No hay otra combinación de L y K que haga 100 unidades a un costo menor.

¿Qué pasa si la firma necesita producir más, digamos, 110 unidades de producción?

PASO Cambiar la celda B18 a 110.

El gráfico se actualiza, mostrando un nuevo isoquante (rojo). La combinación inicial no es una opción viable porque no puede producir 110 unidades. La firma tiene que volver a optimizar.

STEP Ejecute Solver para encontrar la nueva solución óptima.

Las cantidades minimizadas de costos de mano de obra y aumento de capital para producir el mayor rendimiento requerido y el costo total mínimo es ahora de $513.39. Estamos buscando el costo total mínimo. Queremos conocer la forma más barata de producir cualquier salida dada. A esto se le llama la función de costo.

Podemos mostrar el análisis estadístico comparativo en la gráfica isocuante-isocosto o en una gráfica de presentación donde trazamos\(TC\mbox{*}=f(q)\), ceteris paribus. Si conectáramos los puntos de tangencia de isocuantes e isocostos, obtendríamos la ruta de expansión de menor costo (LCEP).

Nuestro trabajo hasta el momento ha revelado dos puntos sobre la función LCEP y costo: cuando q = 100, TC = $464.38 y cuando q = 100, TC = $513.39. Usemos el Asistente de Estadística Comparativa para obtener más datos para que podamos dibujar las funciones LCEP y costo y entender cómo están relacionadas.

PASO Devuelve la celda B18 a 100, luego ejecuta el Asistente de Estática Comparativa, aplicando choques de 10 q en incrementos de 10.

La hoja CS1 muestra cómo deberían ser tus resultados. La hoja CS1 incluye dos gráficas, la gráfica isocuante-isocosto con la ruta de expansión de menor costo y la función costo, como se muestra en la Figura 11.10.

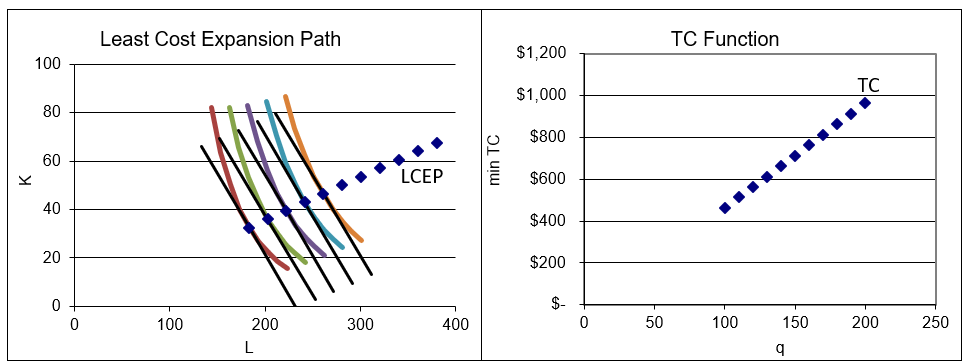
Figura 11.10: Derivando la función de costo.

Fuente: DerivingCostFunction.xls! CS1

La Figura 11.10 debería recordarle otras gráficas que hemos dibujado, como Engel y curvas de demanda. A la izquierda, usando la visualización de la solución óptima al problema de minimización de costos de entrada, mostramos cómo diferentes q producen un conjunto de puntos de tangencia que comprenden el LCEP.

A la derecha en la Figura 11.10, mostramos solo el costo mínimo de producir cada nivel de q, y escondemos todo lo demás. Esto nos permite resaltar la relación entre TC y q.

Las dos gráficas de la Figura 11.10 dejan claro que la fuente de la función de costo es la solución óptima del problema de minimización de costos ya que q varía. Al igual que las curvas de demanda no salen de la nada, sino que se derivan de la maximización de servicios públicos, las funciones de costo se derivan de la minimización de costos de entrada.

Nos interesa la forma de la función de costo. Parece una línea, pero ¿es realmente lineal? Para averiguarlo, podemos ver si tiene una pendiente constante. Si la pendiente está cambiando, sabemos que la función no es lineal.

PASO En su hoja CS, encuentre la pendiente en diferentes puntos de la función calculando el cambio en TC dividido por el cambio en q.

Haga clic en el botón (cerca de la celda C9 en la hoja CS1) si está atascado o para verificar su trabajo. Está claro que la pendiente cambia a medida que cambia la salida. Esto significa que la función de costo es no lineal.

Métodos analíticos para derivar la función de costo

Podemos usar el método Lagrangean para encontrar\(TC\mbox{*} = f(q)\). Dejaremos q como una letra en lugar de un número para que la solución de forma reducida incluya q. Entonces podemos enchufar cualquier valor de q para encontrar el costo mínimo para ese q y dibujar fácilmente una gráfica de la función de costo.

La solución sigue de cerca el trabajo que hicimos al inicio de este capítulo, pero procedemos paso a paso para practicar y reforzar el método lagrangeo.

El problema es\[\begin{gathered} %star suppresses line # \min\limits_{L,K}TC=2L+3K\\ \textrm{s.t. } q = L^{0.75}K^{0.2}\end{gathered}\] El primer paso es reescribir la restricción para que sea igual a cero. \[q - L^{0.75}K^{0.2}=0\]El segundo paso es formar el Lagrangean agregando lambda,\(\lambda\), veces la restricción reescrita a la función objetiva original. Utilizamos una L extra grande para la función lagrangea que no está en absoluto relacionada con la L para el trabajo de parto. \[\begin{gathered} %star suppresses line # \min\limits_{L,K, \lambda}{\large\textit{L}}=2L+3K + \lambda (q- L^{0.75}K^{0.2})\end{gathered}\]El tercer paso para encontrar la solución óptima es tomar la derivada del Lagrangean con respecto a cada variable endógena y establecer cada derivada a cero (dándonos las condiciones de primer orden).

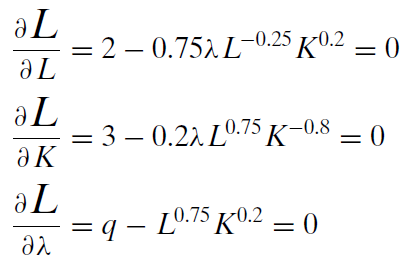
El cuarto, y último, paso es resolver este sistema de ecuaciones para\(L\mbox{*}\),\(K\mbox{*}\), y\(\lambda \mbox{*}\). Movemos los términos con lambda en las dos primeras ecuaciones hacia el lado derecho y luego dividimos la primera ecuación por la segunda. Los exponentes cancelan muy bien (ver sección 11.1) y obtenemos\(L = 5.625K\). Esta no es una solución de forma reducida porque L no es una función solo de variables exógenas. Sustituimos esta expresión por L en la tercera condición de primer orden para obtener K óptima y luego L óptima como se muestra a continuación.

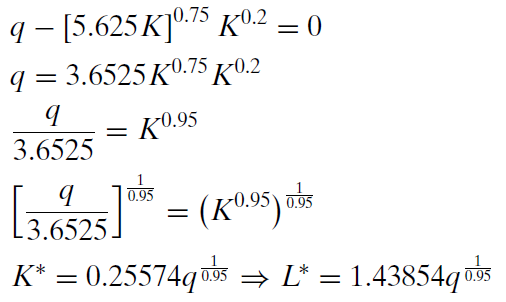
Finalmente, sustituimos las soluciones óptimas por\(L\mbox{*}\) y\(K\mbox{*}\) en la función objetiva original.

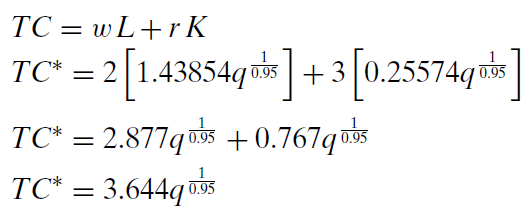
Esta expresión es la función de costo total. Da el costo más barato de producir cualquier cantidad dada de producción. Si q = 100, TC = $464.38. No es sorprendente que esto concuerde con nuestros resultados utilizando métodos numéricos.

Observe también que la función de costo es claramente no lineal. Está aumentando a un ritmo creciente debido a que el exponente en q es mayor que uno (\(\frac{1}{0.95} \approx 1.05\)). La derivada de TC con respecto a q, la pendiente, no es constante porque depende de q. Si el exponente fuera exactamente 1, entonces la pendiente sería constante y el TC sería una línea. El hecho de que este exponente sea sólo ligeramente mayor que uno explica por qué TC se ve casi lineal en la Figura 11.10.

Interpretación de puntos fuera de la función de costo

Cuando derivamos la curva de demanda del problema de optimización de “maximizar la utilidad sujeta a una restricción presupuestaria”, exploramos lo que significaba estar fuera de la curva de demanda (ver Figura 4.12). Aprendimos que los puntos a la izquierda o derecha de la curva de demanda inversa (con el precio en el eje y) significan que el consumidor no está optimizando, es decir, el consumidor no está eligiendo un punto de tangencia entre la curva de indiferencia y la restricción presupuestal.

Podemos realizar el mismo tipo de indagación aquí, haciendo esta pregunta: ¿Qué significa estar fuera de la función de costo?

A diferencia de la curva de demanda inversa, donde la variable exógena se encuentra en el eje y, la función de costo se grafica de acuerdo con la convención matemática habitual, con la variable exógena, output, en el eje x. Así, los puntos fuera de la curva se interpretan verticalmente por encima o por debajo de la función de costo.

¿Qué significa si un punto está por encima de la curva de costo? La Figura 11.11 nos ayuda a responder a esta pregunta. A la izquierda se encuentra la gráfica familiar de isocuantes/isocostos. La forma más barata de producir q0 unidades de salida es con la combinación L y K en el punto etiquetado\(TC\mbox{*}\). El gráfico a la derecha de la Figura 11.11 muestra que\(TC\mbox{*}\) es el punto en la función de costo a una salida de q0.

Figura 11.11: Comprensión de puntos fuera de la función de costo.

El punto Z, un punto por encima de la función de costo, revela que la empresa está produciendo el nivel de producción q0 a un costo total por encima del costo total mínimo. Esto significa que la firma está eligiendo una mezcla de entrada que no minimice los costos. El punto Z de la gráfica de la izquierda de la Figura 11.11 debe estar sobre un isocosto por encima del isocosto tangente. No sabemos exactamente dónde está el punto Z en la gráfica de la izquierda (por lo que no sabemos si hay ineficiencia técnica o asignativa), pero sí sabemos que tiene que estar en algún lugar del isocosto etiquetado TcZ que tenga un costo total igual al costo de producir el punto Z (en la gráfica de la derecha).

El punto Y del lado derecho de la Figura 11.11 está por debajo de la función de costo. ¿Cómo se puede generar este punto por la gráfica de la izquierda? No puede. Hay un isocosto con un costo total igual al del punto Y, pero está por debajo del isocuante y, por lo tanto, inalcanzable. Es decir, el punto Y en realidad no existe. La empresa no puede producir q0 unidades de producción a ningún costo menor que\(TC\mbox{*}\).

Otra forma de pensar el TC geométricamente, es que hay puntos por encima de TC, pero solo espacio vacío debajo de él. Claro, en una página impresa, pizarra o pantalla de computadora, hay un espacio en blanco por encima y por debajo de TC y puedes escribir en él (igual que el punto Y en la Figura 11.11), pero esto es engañoso. De hecho, por debajo de TC no hay nada, nulo total. Si trataras de poner un punto ahí, ¡tu mano pasaría por el papel!

Esto tiene implicaciones más allá de la teoría pura. El hecho de que no haya puntos por debajo de la función de costo significa que nunca debemos ajustar una línea a través de una nube de puntos para estimar una función de costo. En lugar de un enfoque de mínimos cuadrados para estimar una función de costo, las técnicas de estimación en la literatura de frontera estocástica se basan en ajustar una curva alrededor de los puntos observados, como en la Figura 11.12.

Figura 11.12: Estimación de una función de costo.

Turnos en la Función de Costo

Aprendiste en Economía Introductoria que el precio provoca un movimiento a lo largo de una curva de demanda, pero otros choques (como aumentar los ingresos) cambian la demanda provocando que toda la curva cambie. Lo mismo sucede con la función de costo. Cambiar q lleva a moverse a lo largo de la función TC, pero otras variables exógenas provocan cambios en la función de costo.

PASO Proceder a la hoja CostFn.

La hoja muestra una función de costo trazada a partir de los datos anteriores. Los datos en las columnas L y M son en realidad fórmulas para las expresiones de forma reducida para\(L\mbox{*}\) y\(K\mbox{*}\). La columna N tiene el costo total mínimo para el problema de referencia y no cambiará porque las celdas son meramente números (por lo que se etiqueta “Muerto (Inicial)”). La columna O, sin embargo, tiene la expresión de forma reducida para\(TC\mbox{*}\) y se actualizará si se cambia alguno de los parámetros subyacentes (de ahí la etiqueta “Live”).

PASO Haga clic en algunas celdas en las columnas L, M, N y O para ver las fórmulas y valores.

Las versiones generales de las formas reducidas para las funciones de producción de Cobb-Douglas se proporcionan y se ingresan en celdas. Las expresiones parecen desalentadoras (y son tediosas de derivar), pero la derivación es sencilla: deje cada variable exógena como una letra y encuentre la solución óptima para L\(\lambda\), K y costo total.

Inicialmente, N y O son los mismos porque los valores de las variables exógenas aún no se han cambiado. Hagámoslo ahora.

PASO Cambiar la celda B20, el exponente en L, a 0.8.

Tu pantalla se parece a la Figura 11.13. El incremento en la productividad laboral se ha desplazado hacia abajo en la curva de costo total. Esto tiene sentido. El incremento en c ha hecho que sea más barato producir cualquier salida dada.

Figura 11.13: El costo total cambia a la baja cuando aumenta la productividad laboral.

Fuente: DerivingCostFunction.xls! CostFn

Se puede experimentar con otros choques a la función de costo. Cambie los precios de entrada, los exponentes de entrada o A para ver cómo cambia la función de costo. Haga clic en el botón o ctrl-z (deshacer) después de cada prueba. Conecta lo que ves en la pantalla con el choque que aplicaste. Los cambios en q no tienen ningún efecto visible porque simplemente se mueve a lo largo de la función de costo.

Interpretación\(\lambda \mbox{*}\)

Terminamos este capítulo mostrando que el multiplicador lagrageano,\(\lambda \mbox{*}\) tiene una interpretación útil en el problema de minimización de costos de entrada. Veremos que\(\lambda \mbox{*}\) da una manera más fácil de derivar una función de costo que resolver el problema de minimización de costos restringidos con q como letra y hallazgo\(TC\mbox{*} = f(q)\).

El atajo de función de costo utiliza el hecho de que\(\lambda \mbox{*}\) da la tasa instantánea de cambio en el valor óptimo de la función objetivo a medida que varía la restricción. Por lo tanto,\(\lambda \mbox{*}\) señala cómo la relajación de la restricción impactaría en la meta.

Para la maximización de servicios públicos, podríamos relajar la restricción aumentando los ingresos. La restricción presupuestal en el Lagrangean es\(m - p_1x_1 - p_2x_2 = 0\) así a medida que m suba, el consumidor podrá alcanzar una mayor utilidad máxima. El multiplicador lagrangeo nos dice cuánta más utilidad se gana a medida que aumentan los ingresos. Desafortunadamente, la utilidad es ordinal por lo que\(\lambda \mbox{*}\) no tiene una interpretación útil en la Teoría del Comportamiento del Consumidor.

Las cosas son diferentes en el problema de minimización de costos de entrada restringidos. La función objetiva en este caso es el costo total mínimo y se mide en una escala cardinal. Podemos observar directamente el costo total mínimo y comparar de manera significativa cómo cambia dentro de una empresa y entre empresas. Esto significa que podemos aplicar la interpretación de\(\lambda \mbox{*}\) a la minimización de costos de entrada.

La restricción en el Lagrangean es\(q - f(L,K)\). Si variamos la restricción haciendo que la empresa produzca una unidad más de producción, sabemos que el costo total aumentaría a medida que nos movemos a una isocuante más alta. El valor de nos\(\lambda \mbox{*}\) dice por cuánto subiría el costo total mínimo.

Por ejemplo, a q = 100 en DerivingCostFunction.xls,\(\lambda \mbox{*}\) es de aproximadamente $4.89. Puedes confirmarlo por métodos numéricos (usando el Solver de Excel y obteniendo el Informe de Sensibilidad) o por métodos analíticos, resolviendo\(\lambda \mbox{*}\) desde las tres condiciones de primer orden. De cualquier manera, obtendrás (casi exactamente) la misma respuesta.

Pero, ¿qué nos dice esto? El valor de $4.89 significa que si aumentamos la producción en una cantidad infinitesimalmente pequeña, el costo total mínimo subirá 4,89 veces más. Usemos Excel para trabajar en esto.

PASO Haga clic en el botón de la hoja CostFn y eche un vistazo a la celda resaltada con fondo amarillo (P8). Da click en él y lee la fórmula.

El valor de P8 es de $4.99. Eso está cerca del valor\(\lambda \mbox{*}\) de $4.89, pero no exactamente lo mismo. ¿Qué está pasando?

PASO Vaya a la hoja CS1 y eche un vistazo a la celda resaltada, de fondo amarillo (E15) (haga clic en el botón si es necesario). Su valor es de $4.90.

Esto está mucho más cerca\(\lambda \mbox{*}\) del valor's de $4.89. ¿Por qué? Porque el cambio en q es mucho menor en la hoja CS1 que en la hoja CostFn. A medida que el cambio en q se acerca a cero, el cambio en\(TC\mbox{*}\) dividido por el cambio en q se acercará\(\lambda \mbox{*}\).

PASO Regresar a la hoja CostFn y cambiar la celda K8 de 200 a 110. Esto replica el valor de la hoja CS1 para\(\lambda \mbox{*}\). A continuación, establezca K8 en 101. ¿Qué ves?

Con K8 ajustado a 101 para que\(\Delta q = 1\),\(\frac{\Delta TC}{\Delta q} = \$4.89\), el valor de\(\lambda \mbox{*}\). Bueno, en realidad, no exactamente 4.89 dólares. Si mostráramos más decimales en P8 y calculamos el valor de\(\lambda \mbox{*}\) a más decimales, los dos no estarían de acuerdo. Pero se acercarían cuanto más pequeños hiciéramos\(\Delta q\).

Por supuesto, esto no es más que una demostración de la idea del derivado. Si te desconcierta cómo\(\frac{\Delta TC}{\Delta q}\) puede estar tan cerca de\(\lambda \mbox{*}\) en la hoja CS1 (una diferencia de un centavo parece bastante pequeña), dado que el cambio en q es de 10 unidades (que apenas es infinitesimalmente pequeño), la respuesta está en la función de costo total: It simplemente no es muy curvilíneo. Porque\(TC \mbox{*}\) sigue casi (pero no del todo) una línea recta, calcular la pendiente de q = 100 a q = 110 está cerca de la pendiente de la línea tangente en q = 100.

El propósito del trabajo anterior era convencerte de eso\(\lambda \mbox{*} = \frac{dTC}{dq}\). El multiplicador Lagrangean da la tasa instantánea de cambio en el costo total mínimo con respecto a la salida.

PASO Puede confirmar la afirmación de que\(\lambda \mbox{*} = \frac{dTC}{dq}\) cambiando los parámetros en la hoja CostFn y manteniendo su ojo en la celda de fondo rosa H31. Calcula la diferencia entre\(\lambda \mbox{*}\) en H13 y\(\frac{dTC}{dq}\) en H30. La diferencia siempre es cero porque estas dos cosas,\(\lambda \mbox{*}\) y\(\frac{dTC}{dq}\) son equivalentes.

Podrías preguntar: “¿Y qué?” En otras palabras, ¿qué podemos hacer con el conocimiento de eso\(\lambda \mbox{*} = \frac{dTC}{dq}\)? Mucho. Por un lado, podemos derivar fácilmente la función de costo. Después de todo, la tasa de cambio en el costo total a medida que cambia la producción es el costo marginal (MC). Así,\(\lambda \mbox{*} = \frac{dTC}{dq} = MC(q)\). Esto significa que podemos obtener fácilmente la función de costo total simplemente integrándonos\(\lambda \mbox{*}\) con respecto a q.

Además, como veremos cuando resolvamos el problema de maximización del beneficio de la producción, generalmente queremos ingresos marginales y costos marginales, por lo que saber que\(\lambda \mbox{*} = \frac{dTC}{dq}\) puede ser un verdadero atajo. Si tenemos\(\lambda \mbox{*}\), entonces no tenemos que derivar\(TC\mbox{*} = f(q)\) y luego tomar la derivada para obtener MC.

La función de costo tiene padres

En esta sección se incluyeron algunas ideas complicadas, pero terminamos priorizando las cosas. No cabe duda de que la idea más importante es que la función de costo tiene una fuente y no aparece de la nada. Esto es capturado por la Figura 11.10, la función de costo se deriva haciendo un análisis estadístico comparativo sobre el problema de minimización de costos de entrada.

Aunque a menudo nos interesa la respuesta de una variable endógena a un choque, la estadística comparativa en el problema de minimización de costos de entrada se enfoca en cómo la función objetiva, el costo total mínimo, se ve afectada por el shock q. El costo total mínimo en función de q es la función de costo.

Al explicar lo que significa estar por encima o por debajo de la función de costo en términos de la gráfica isocuante-isocosto, enfatizamos la idea de que la función de costo muestra la forma más barata de producir cualquier producto dado. Una buena manera de recordar esto es reflexionar sobre el hecho llamativo de que no hay espacio por debajo de la función de costo, lo que significa que es imposible producir la salida dada más barata que la forma más barata posible.

Los cambios en otros parámetros además de la salida hacen que toda la función de costo se desplace porque el costo total mínimo depende de todas las variables exógenas. Si q cambia, nos movemos a lo largo de la función de costo; otros choques cambian TC.

Finalmente, explicamos una idea matemáticamente sofisticada:\(\lambda \mbox{*}\) proporciona información sobre la tasa de cambio del valor óptimo de la función objetiva a medida que la restricción se relaja. Esta interpretación del multiplicador lagrangeo se mantiene para cada problema de optimización restringida.

No aplicamos esta interpretación en la Teoría del Comportamiento del Consumidor porque la utilidad (la función objetiva) no puede medirse cardinalmente. En los viejos tiempos, cuando se creía que la utilidad se midía cardinalmente en utils,\(\lambda \mbox{*}\) era la utilidad marginal del dinero. \(\lambda \mbox{*}\)te diría la tasa de cambio en la utilidad máxima si le diste al consumidor un incremento infinitesimal en los ingresos.

Dado que el costo total es directamente observable y contable,\(\lambda \mbox{*}\) puede interpretarse correctamente como costo marginal,\(\frac{dTC}{dq}\). Esto da un atajo a la función de costo y MC.

Ejercicios

1. Con la función de producción\(q = L^{0.75} K^{0.5}\),, y las variables exógenas w = 2, r = 3, usa Excel para crear una gráfica de la función de costo para los mismos valores q que el de la hoja CS1. Copia y pega tu gráfica en un documento de Word.

2. ¿En qué se diferencia la función de costo que acabas de derivar de la de la hoja CS1? ¿Cuál es la variable responsable de generar esta diferencia?

3. De las funciones de costo en la hoja CS1 y la pregunta 1, ¿qué se puede deducir sobre las funciones de costo derivadas de las funciones de producción de Cobb-Douglas?

4. Si alguien resuelve un problema de minimización de costos de entrada y encuentra que\(\lambda \mbox{*}\) = 50, ¿qué significa esto?

Referencias

El epígrafe es de la página 333 de Hans Staehle, “La medición de las funciones estadísticas de costos: una valoración de algunas contribuciones recientes”, The American Economic Review, Vol. 32, núm. 2, primera parte (junio de 1942), pp. 321—333, www.jstor.org/stable/1803513. Staehle se mostró optimista en 1942 de que los avances en estadísticas y recolección de datos permitirían a los economistas estimar las funciones de costos para industrias particulares. Desafortunadamente, es justo decir que el sueño de Staehle de descubrir formas funcionales flexibles sigue sin cumplirse. El trabajo empírico sobre las funciones de costos generalmente encuentra que las empresas enfrentan costos totales lineales (o casi lineales) (produciendo costos promedio horizontal y marginales) en grandes rangos de producción.