Conjunto de Problemas 1: Usar Elasticidades para Variables Exogneas para Estimar Choques y Cambios en un Equilibrio. En este conjunto de problemas se puede suponer que es apropiado tratar W y M como variables exógenas.
Ejercicio\(\PageIndex{1}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 0.5\)
\(\phi_{1W} = -0.15\)
\(\varepsilon_{11} = -1.5\)
\(\varepsilon_{1M} = -0.5\)
\(\% \Delta M = 6\)
\(\% \Delta W = 0\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= 0\)
\(\textrm{Demand Shock}: D= -3\)
\(\% \Delta P_{1} = -1.5\)
\( \% \Delta Q_{1} = -0.75\)
Ejercicio\(\PageIndex{2}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 1.5\)
\(\phi_{1W} = -0.25\)
\(\varepsilon_{11} = -1.75\)
\(\varepsilon_{1M} = 0.5\)
\(\% \Delta M = 5\)
\(\% \Delta W = 3\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= -0.75\)
\(\textrm{Demand Shock}: D= 2.5\)
\(\% \Delta P_{1} = 1\)
\( \% \Delta Q_{1} = 0.75\)
Ejercicio\(\PageIndex{3}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 0.5\)
\(\phi_{1W} = -0.3\)
\(\varepsilon_{11} = -2\)
\(\varepsilon_{1M} = -0.4\)
\(\% \Delta M = 8\)
\(\% \Delta W = 0\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= 0\)
\(\textrm{Demand Shock}: D= -3.2\)
\(\% \Delta P_{1} = -1.28\)
\( \% \Delta Q_{1} = -0.64\)
Ejercicio\(\PageIndex{4}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 2\)
\(\phi_{1W} = -0.1\)
\(\varepsilon_{11} = -3\)
\(\varepsilon_{1M} = 0.3\)
\(\% \Delta M = 0\)
\(\% \Delta W = 8\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= -0.8\)
\(\textrm{Demand Shock}: D= 0\)
\(\% \Delta P_{1} = 0.16\)
\( \% \Delta Q_{1} = -0.48\)
Ejercicio\(\PageIndex{5}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 0.5\)
\(\phi_{1W} = -0.2\)
\(\varepsilon_{11} = -1.5\)
\(\varepsilon_{1M} = 0.4\)
\(\% \Delta M = 5\)
\(\% \Delta W = 4\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= -0.8\)
\(\textrm{Demand Shock}: D= 2\)
\(\% \Delta P_{1} = 1.4\)
\( \% \Delta Q_{1} = -0.1\)
Ejercicio\(\PageIndex{6}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 0.25\)
\(\phi_{1W} = -0.3\)
\(\varepsilon_{11} = -1.75\)
\(\varepsilon_{1M} = 0.5\)
\(\% \Delta M = 0\)
\(\% \Delta W = 8\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= -2.4\)
\(\textrm{Demand Shock}: D= 0\)
\(\% \Delta P_{1} = 1.2\)
\( \% \Delta Q_{1} = -2.1\)
Ejercicio\(\PageIndex{7}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 1\)
\(\phi_{1W} = -0.5\)
\(\varepsilon_{11} = -2\)
\(\varepsilon_{1M} = -0.5\)
\(\% \Delta M = 5\)
\(\% \Delta W = 8\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= -4\)
\(\textrm{Demand Shock}: D= -2.5\)
\(\% \Delta P_{1} = 0.5\)
\( \% \Delta Q_{1} = -3.5\)
Ejercicio\(\PageIndex{8}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 0.5\)
\(\phi_{1W} = -0.7\)
\(\varepsilon_{11} = -3\)
\(\varepsilon_{1M} = 0.4\)
\(\% \Delta M = 0\)
\(\% \Delta W = 2\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= -1.4\)
\(\textrm{Demand Shock}: D= 0\)
\(\% \Delta P_{1} = 0.4\)
\( \% \Delta Q_{1} = -1.2\)
Ejercicio\(\PageIndex{9}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 1.5\)
\(\phi_{1W} = -0.5\)
\(\varepsilon_{11} = -1.75\)
\(\varepsilon_{1M} = -0.6\)
\(\% \Delta M = 5\)
\(\% \Delta W = 6\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= -3\)
\(\textrm{Demand Shock}: D= -3\)
\(\% \Delta P_{1} = 0\)
\( \% \Delta Q_{1} = -3\)
Ejercicio\(\PageIndex{10}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 0.75\)
\(\phi_{1W} = -0.2\)
\(\varepsilon_{11} = -1.75\)
\(\varepsilon_{1M} = -0.4\)
\(\% \Delta M = 7\)
\(\% \Delta W = 0\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S= 0\)
\(\textrm{Demand Shock}: D= -2.8\)
\(\% \Delta P_{1} = -1.12\)
\( \% \Delta Q_{1} = -0.84\)
Conjunto de Problemas 2: Uso de Estimaciones de Costo por Unidad o Valoración para Calcular Choques y Cambios en un Equilibrio
Ejercicio\(\PageIndex{1}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 1.5\)
\(\varepsilon_{11} = -1\)
\(\textrm{Per unit change in production cost is } 8 \%\)
\(\textrm{Per unit change in willingness to pay is } = 3 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = -12\)
\(\textrm{Demand Shock}: D = 3\)
\(\% \Delta P_{1} = 6\)
\(\% \Delta Q_{1} = -3\)
Ejercicio\(\PageIndex{2}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 1\)
\(\varepsilon_{11} = -2\)
\(\textrm{Per unit change in production cost is } 0 \%\)
\(\textrm{Per unit change in willingness to pay is } = -6 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = 0\)
\(\textrm{Demand Shock}: D = -12\)
\(\% \Delta P_{1} = -4\)
\(\% \Delta Q_{1} = -4\)
Ejercicio\(\PageIndex{3}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 0.5\)
\(\varepsilon_{11} = -2\)
\(\textrm{Per unit change in production cost is } 6 \%\)
\(\textrm{Per unit change in willingness to pay is } = 7 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = -3\)
\(\textrm{Demand Shock}: D = 14\)
\(\% \Delta P_{1} = 6.8\)
\(\% \Delta Q_{1} = 0.4\)
Ejercicio\(\PageIndex{4}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 2\)
\(\varepsilon_{11} = -6\)
\(\textrm{Per unit change in production cost is } -2 \%\)
\(\textrm{Per unit change in willingness to pay is } = -3 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = 4\)
\(\textrm{Demand Shock}: D = -18\)
\(\% \Delta P_{1} = -2.75\)
\(\% \Delta Q_{1} = -1.5\)
Ejercicio\(\PageIndex{5}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 2\)
\(\varepsilon_{11} = -3\)
\(\textrm{Per unit change in production cost is } 0 \%\)
\(\textrm{Per unit change in willingness to pay is } = 5 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = 0\)
\(\textrm{Demand Shock}: D = 15\)
\(\% \Delta P_{1} = 3\)
\(\% \Delta Q_{1} = 6\)
Ejercicio\(\PageIndex{6}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 1.5\)
\(\varepsilon_{11} = -1.75\)
\(\textrm{Per unit change in production cost is } -5 \%\)
\(\textrm{Per unit change in willingness to pay is } = -5 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = 9\)
\(\textrm{Demand Shock}: D = -10.5\)
\(\% \Delta P_{1} = -6\)
\(\% \Delta Q_{1} = 0\)
Ejercicio\(\PageIndex{7}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 1\)
\(\varepsilon_{11} = -4\)
\(\textrm{Per unit change in production cost is } -4 \%\)
\(\textrm{Per unit change in willingness to pay is } = 0 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = 4\)
\(\textrm{Demand Shock}: D = 0\)
\(\% \Delta P_{1} = -0.8\)
\(\% \Delta Q_{1} = 3.2\)
Ejercicio\(\PageIndex{8}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 2\)
\(\varepsilon_{11} = -3\)
\(\textrm{Per unit change in production cost is } -6 \%\)
\(\textrm{Per unit change in willingness to pay is } = 0 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = 12\)
\(\textrm{Demand Shock}: D = 0\)
\(\% \Delta P_{1} = -2.4\)
\(\% \Delta Q_{1} = 7.2\)
Ejercicio\(\PageIndex{9}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 1.5\)
\(\varepsilon_{11} = -1.75\)
\(\textrm{Per unit change in production cost is } 5 \%\)
\(\textrm{Per unit change in willingness to pay is } = 5 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = -7.5\)
\(\textrm{Demand Shock}: D = 8.75\)
\(\% \Delta P_{1} = 5\)
\(\% \Delta Q_{1} = 0\)
Ejercicio\(\PageIndex{10}\)
Teniendo en cuenta lo siguiente:
\(\phi_{11} = 0.5\)
\(\varepsilon_{11} = -0.75\)
\(\textrm{Per unit change in production cost is } 6 \%\)
\(\textrm{Per unit change in willingness to pay is } = -7 \%\)
¿Cuál es el choque de suministro?
¿Cuál es el choque de demanda?
¿Cuál es el cambio en el precio de equilibrio?
¿Cuál es el cambio en la cantidad de equilibrio?
- Responder
-
\(\textrm{Supply Shock}: S = -3\)
\(\textrm{Demand Shock}: D = -5.25\)
\(\% \Delta P_{1} = -1.8\)
\(\% \Delta Q_{1} = -3.9\)
Juego de problemas 3: Opción múltiple
Ejercicio\(\PageIndex{1}\)
- ¿Cuál describe mejor un equilibrio de mercado?
a) Un precio tal que la cantidad suministrada sea igual a la cantidad demandada.
b) La confluencia de factores exógenos que alteran las condiciones dentro del mercado en cuestión.
c) Fuerzas que provoquen cambios de precio y/o cantidad en un mercado.
d) Una situación en la que los precios alcanzan lo que muchos consideran niveles razonables. Por ejemplo, el mercado de la gasolina finalmente ha vuelto a un equilibrio después de varios años de altos precios.
- Responder
-
a
Ejercicio\(\PageIndex{2}\)
- En modelos de equilibrio, variables endógenas
a) Son variables que provocan cambios en las curvas de demanda y oferta.
b) Se están analizando los precios y cantidades en los mercados.
c) Son inexistentes porque todas las variables son exógenas en estos modelos.
d) Son difíciles de medir pero aún afectan el equilibrio (e.g., cambios en las preferencias).
- Responder
-
b
Ejercicio\(\PageIndex{3}\)
- Si estás modelando un equilibrio de mercado y necesitas dar cuenta de los comentarios de otros mercados o sectores de la economía, entonces deberías estar usando
a) Un modelo de equilibrio parcial.
b) Un modelo de rendición de cuentas por retroalimentación.
c) Un modelo de equilibrio general.
d) Un modelo que obliga a que las elasticidades cruzadas de precios sean negativas.
- Responder
-
c
Ejercicio\(\PageIndex{4}\)
- Considera un mercado único. ¿Cuál sería más probable que provocara un aumento tanto en el precio de equilibrio como en la cantidad de equilibrio?
a) Un choque de suministro positivo
b) Una disminución en los ingresos del consumidor, asumiendo que la demanda es de un bien inferior
c) Una disminución en los ingresos del consumidor, asumiendo que la demanda es de un bien normal
d) Un choque de suministro negativo
- Responder
-
b
Utilice el siguiente escenario para responder a las preguntas 5 a 8.
Dos productos son sustitutos en el consumo y no están relacionados en la producción. Ucrania es una fuente importante de suministro para el Producto 1. Dado el conflicto actual en el este de Ucrania, la oferta para el Producto 1 (Mercado 1) se desplaza hacia adentro (hacia la izquierda).
Ejercicio\(\PageIndex{5}\)
- ¿Cuál de las siguientes cosas sabe que sucederá en el Mercado 1?
a) Aumentará la cantidad de equilibrio en el Mercado 1
b) Disminuirá el precio de equilibrio en el Mercado 1
c) Incrementará el precio de equilibrio en el Mercado 1
d) Tanto a como c
- Responder
-
c
Ejercicio\(\PageIndex{6}\)
- ¿Cuál de los siguientes sabes que sucederá en Market 2?
a) Nada porque el choque de oferta estaba en el Mercado 1.
b) Incrementará el precio de equilibrio en el Mercado 2
c) Disminuirá el precio de equilibrio en el Mercado 2
d) Aumentará la cantidad de equilibrio en el Mercado 2
e) Tanto b como d.
- Responder
-
e
Ejercicio\(\PageIndex{7}\)
- Después de considerar la retroalimentación entre estos dos mercados. ¿Cuál, en su caso, de los siguientes horarios no ha cambiado una vez que se alcanza un nuevo equilibrio?
a) Abastecimiento en el Mercado 1
b) Abastecimiento en el Mercado 2
c) Demanda en el Mercado 1
d) Demanda en el Mercado 2
e) Todos los horarios anteriores han cambiado
- Responder
-
b
Ejercicio\(\PageIndex{8}\)
- ¿Cuál describe mejor el choque exógeno en esta situación?
a) El conflicto que llevó al cambio de oferta al Mercado 1
b) El cambio en el precio de equilibrio en el Mercado 1
c) La retroalimentación del Mercado 2 al Mercado 1
d) Todo lo anterior.
- Responder
-
a
Utilice el diagrama a continuación para responder a las preguntas 9 - 12.
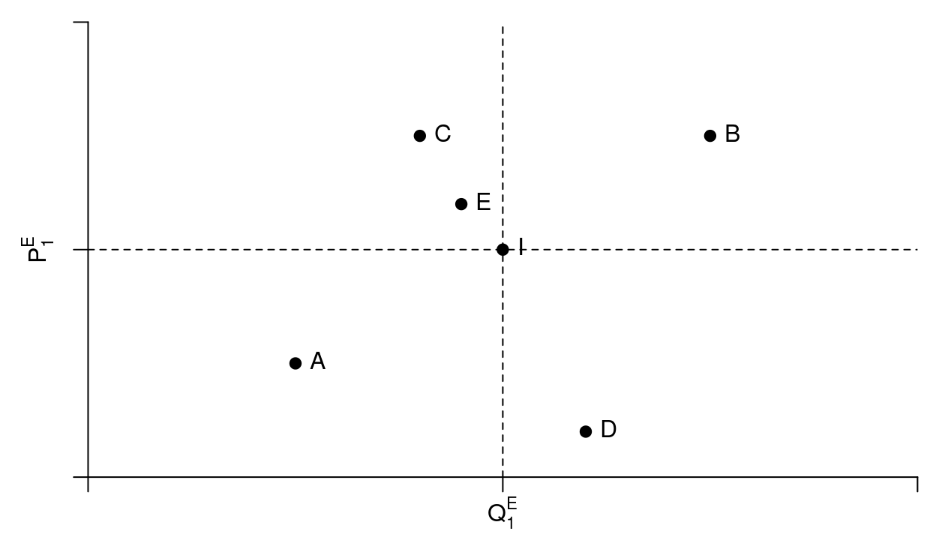
Ejercicio\(\PageIndex{9}\)
- Solo punto D
- Puntos C, D y E
- Puntos B y A
- Puntos C y E
- Ninguno de los puntos
- Responder
-
c
Ejercicio\(\PageIndex{10}\)
- ¿En qué casos sabe con certeza que la demanda ha aumentado en relación con el equilibrio original en el punto I?
a) Punto B
b) Puntos C y E
c) Puntos B y A
d) Puntos A
e) Ninguno de los puntos
- Responder
-
a
Ejercicio\(\PageIndex{11}\)
- ¿En qué casos sabe con certeza que la oferta ha disminuido en relación con el equilibrio original en el punto I?
a) Punto B
b) Puntos C y E
c) Puntos B y A
d) Puntos A
e) Ninguno de los puntos
- Responder
-
b
Ejercicio\(\PageIndex{12}\)
- ¿En qué casos sabe con certeza que tanto la demanda como la oferta se han desplazado del equilibrio original en el punto I?
a) Punto B
b) Puntos C y E
c) Puntos B y A
d) Puntos A
e) Ninguno de los puntos
- Responder
-
e



