4.5: El Sandwich de la Coneccionista

Tanto la neurona McCulloch-Pitts (McCulloch & Pitts, 1943) como el perceptrón (Rosenblatt, 1958, 1962) utilizaron la función de paso Heaviside para implementar la ley todo-orninguno. Como resultado, ambas arquitecturas generaron un juicio “verdadero” o “falso” sobre cada patrón de entrada. Así, ambas arquitecturas son digitales, y su función básica es el reconocimiento de patrones o la clasificación de patrones.

La lógica de dos valores que se introdujo en el Capítulo 2 se puede lanzar en el contexto de dicho reconocimiento digital de patrones. En la lógica de dos valores, las funciones se calculan sobre dos proposiciones de entrada, p y q, que a su vez pueden ser verdaderas o falsas. Como resultado, sólo hay cuatro combinaciones posibles de p y q, las cuales se dan en las dos primeras columnas de la Tabla 4-1. Las funciones lógicas en la lógica de dos valores son en sí mismas juicios de verdadero o falso que dependen de combinaciones de los valores de verdad de las proposiciones de entrada p y q. Como resultado, hay 16 operaciones lógicas diferentes que se pueden definir en la lógica de dos valores; estas fueron proporcionadas en la Tabla 2-2.

Las tablas de verdad para dos de las dieciséis operaciones posibles en la lógica de dos valores se proporcionan en las dos últimas columnas del Cuadro 4-1. Una es la operación AND (p·q), que sólo es verdadera cuando ambas proposiciones son verdaderas. La otra es la operación XOR (pq), que sólo es verdadera cuando una u otra de las proposiciones es verdadera.

p	q	p*q	p^q
1	1	1	0
1	0	0	1
0	1	0	1
0	0	0	0

Cuadro 4-1. Tablas de verdad para las operaciones lógicas AND (pq) y XOR (p q), donde se da el valor de verdad de cada operación como una función de la verdad de cada una de dos proposiciones, p y q. '1' indica “verdadero” y '0' indica “falso”. La notación lógica se toma de McCulloch (1988b).

Ese AND o XOR son ejemplos de reconocimiento digital de patrones puede hacerse más explícito al representar sus tablas de verdad gráficamente como espacios de patrones. En un espacio patrón, una fila completa de una tabla de verdad se representa como un punto en una gráfica. Las coordenadas de un punto en un espacio patrón están determinadas por los valores de verdad de las proposiciones de entrada. El color del punto representa el valor de verdad de la operación calculada sobre las entradas.

La Figura 4-2A ilustra el espacio de patrón para la operación AND de la Tabla 4-1. Tenga en cuenta que tiene cuatro puntos graficados, uno por cada fila de la tabla de verdad. Las coordenadas de cada punto graficado —( 1,1), (1,0), (0,1) y (0,0) —indican los valores de verdad de las proposiciones p y q. La operación AND solo es verdadera cuando ambas proposiciones son verdaderas. Esto se representa coloreando el punto en la coordenada (1,1) negro. Los otros tres puntos son de color blanco, lo que indica que el operador lógico devuelve un valor “falso” para cada uno de ellos.

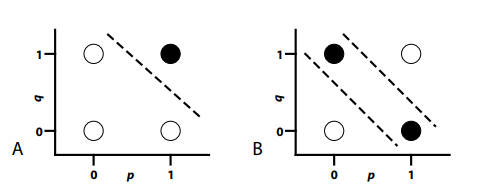
Figura 4-2. (A) Espacio de patrón para Y; (B) Espacio de patrón para XOR.

Los espacios de patrón se utilizan para el reconocimiento digital de patrones tallándolos en regiones de decisión. Si un punto que representa un patrón cae en una región de decisión, entonces se clasifica de una manera. Si ese punto cae en una región de decisión diferente, entonces se clasifica de una manera diferente. Aprender a clasificar un conjunto de patrones implica aprender a tallar correctamente el espacio de patrones en las regiones de decisión deseadas.

El problema AND es un ejemplo de un problema linealmente separable. Esto se debe a que un solo corte recto a través del espacio del patrón lo divide en dos regiones de decisión que generan las clasificaciones de patrón correctas. La línea discontinua en la Figura 4-2A indica la ubicación de este corte recto para el problema AND. Tenga en cuenta que el único patrón “verdadero” cae en un lado de este corte, y que los tres patrones “falsos” caen en el otro lado de este corte.

No todos los problemas son linealmente separables. Un problema linealmente no separable es aquel en el que un solo corte recto no es suficiente para separar todos los patrones de un tipo de todos los patrones de otro tipo. Un ejemplo de un problema linealmente no separable es el problema XOR, cuyo espacio de patrón se ilustra en la Figura 4-2B. Obsérvese que las posiciones de los cuatro patrones en la Figura 4-2B son idénticas a las posiciones de la Figura 4-2A, ya que ambos espacios de patrón involucran las mismas proposiciones. La única diferencia es la coloración de los puntos, lo que indica que XOR implica hacer un juicio diferente al de AND. No obstante, esta diferencia entre gráficas es importante, porque ahora es imposible separar todos los puntos negros de todos los puntos blancos con un solo corte recto. En cambio, se requieren dos cortes diferentes, como lo muestran las dos líneas discontinuas en la Figura 4-2B. Esto significa que XOR no es linealmente separable.

La separabilidad lineal define los límites de lo que puede ser calculado por un perceptrón Rosenblatt (Rosenblatt, 1958, 1962) o por una neurona McCulloch-Pitts (McCulloch & Pitts, 1943). Es decir, si algún problema de reconocimiento de patrones es linealmente separable, entonces cualquiera de estas arquitecturas es capaz de representar una solución a ese problema. Por ejemplo, debido a que AND es linealmente separable, puede ser calculado por un perceptrón, como el ilustrado en la Figura 4-3.

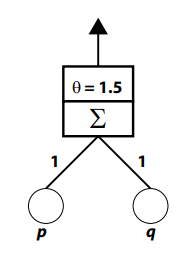
Figura 4-3. Un perceptrón Rosenblatt que puede calcular la operación AND.

Este perceptrón consiste en dos unidades de entrada cuyas actividades representan respectivamente el estado (es decir, 0 o 1) de las proposiciones p y q. Cada una de estas unidades de entrada envía una señal a través de una conexión a una unidad de salida; la cifra indica que el peso de cada conexión es 1. La unidad de salida realiza dos operaciones. Primero, calcula su entrada neta sumando las dos señales que recibe (el componente S de la unidad de salida). Segundo, transforma la entrada neta en actividad aplicando la función de paso Heaviside. La cifra indica en el segundo componente de la unidad de salida que el umbral para esta función de activación (q) es 1.5. Esto significa que la actividad de la unidad de salida solo será 1 si la entrada neta es mayor o igual a 1.5; de lo contrario, la actividad de la unidad de salida será igual a 0.

Si se consideran las cuatro combinaciones diferentes de actividades de unidades de entrada que se presentarían a este dispositivo (1,1), (1,0), (0,1) y (0,0), entonces está claro que la única vez que la actividad de la unidad de salida será igual a 1 es cuando ambas unidades de entrada se activan con 1 (es decir, cuando p y q son verdaderas). Esto se debe a que esta situación producirá una entrada neta de 2, que supera el umbral. En todos los demás casos, la entrada neta será 1 o 0, que será menor que el umbral, y que por lo tanto producirá una actividad de unidad de salida de 0.

La capacidad del perceptrón Figura 4-3 para calcular AND se puede describir en términos del espacio patrón en la Figura 4-2A. El umbral y los pesos de conexión del perceptrón proporcionan la ubicación y orientación del corte recto único que talla el espacio del patrón en regiones de decisión (la línea discontinua en la Figura 4-2A). La activación de las unidades de entrada con algún patrón presenta una ubicación de espacio de patrón al perceptrón. El perceptrón examina esta ubicación para decidir de qué lado del corte se encuentra la ubicación, y responde en consecuencia.

Esta cuenta de espacio de patrón del perceptrón Figura 4-3 también apunta a una limitación. Cuando se utiliza la función de paso Heaviside como función de activación, el perceptrón solo define un solo corte recto a través del espacio del patrón y, por lo tanto, solo puede lidiar con problemas separables linealmente. Un perceptrón similar al ilustrado en la Figura 4-3 no sería capaz de calcular XOR (Figura 4-2B) porque la unidad de salida es incapaz de realizar los dos cortes requeridos en el espacio del patrón.

¿Cómo se extiende el poder computacional más allá del perceptrón? Un enfoque es agregar unidades de procesamiento adicionales, llamadas unidades ocultas, que son intermediarios entre las unidades de entrada y salida. Las unidades ocultas pueden detectar características adicionales que transforman el problema al aumentar la dimensionalidad del espacio del patrón. Como resultado, el uso de unidades ocultas puede convertir un problema linealmente no separable en uno linealmente separable, permitiendo que una sola unidad de salida binaria genere las respuestas correctas.

La Figura 4-4 muestra cómo el circuito AND ilustrado en la Figura 4-3 se puede agregar como una unidad oculta para crear un perceptrón multicapa que puede calcular la operación XOR linealmente no separable (Rumelhart, Hinton, & Williams, 1986a). Este perceptrón también tiene dos unidades de entrada cuyas actividades representan respectivamente el estado de las proposiciones p y q. Cada una de estas unidades de entrada envía una señal a través de una conexión a una unidad de salida; la cifra indica que el peso de cada conexión es 1. El umbral de la función de activación de la salida (q) es 0.5. Si tuviéramos que ignorar la unidad oculta en esta red, la unidad de salida estaría computando OR, encendiéndose cuando una o ambas de las proposiciones de entrada sean verdaderas.

Sin embargo, esta red no calcula OR, porque las unidades de entrada también están conectadas a una unidad oculta, que a su vez envía una tercera señal para ser agregada a la entrada neta de la unidad de salida. La unidad oculta es idéntica al circuito AND de la Figura 4-3. La señal que envía a la unidad de salida es fuertemente inhibitoria; el peso de la conexión entre las dos unidades es —2.

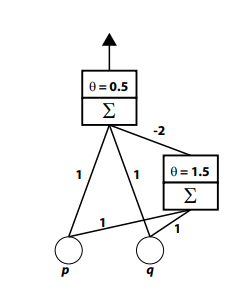
Figura 4-4. Un perceptrón multicapa que puede calcular XOR.

La acción de la unidad oculta es crucial para el comportamiento del sistema. Cuando ninguna o solo una de las unidades de entrada se activa, la unidad oculta no responde, por lo que envía una señal de 0 a la unidad de salida. Como resultado, en estas tres situaciones la unidad de salida se enciende cuando cualquiera de las entradas está encendida (porque la entrada neta está por encima del umbral) y se apaga cuando ninguna de las unidades de entrada está encendida. Cuando ambas unidades de entrada están encendidas, envían una señal excitatoria a la unidad de salida. Sin embargo, también envían una señal que enciende la unidad oculta, provocando que envíe inhibición a la unidad de salida. En esta situación, la entrada neta de la unidad de salida es 1 + 1 — 2 = 0 que está por debajo del umbral, produciendo actividad de unidad de salida cero. Por lo tanto, todo el circuito realiza la operación XOR.

El comportamiento del perceptrón multicapa Figura 4-4 también puede estar relacionado con el espacio patrón de la Figura 4-2B. El corte inferior en ese espacio de patrón es proporcionado por la unidad de salida. El corte superior en ese espacio de patrón es proporcionado por la unidad oculta. La coordinación de las dos unidades permite al circuito resolver este problema linealmente inseparable.

Interpretar las redes en términos de la manera en que tallan un espacio de patrones en regiones de decisión sugiere que el aprendizaje puede describirse como determinar dónde deben realizarse los cortes en un espacio de patrones. Cualquier unidad oculta o de salida que utilice una función monótona no lineal como Heaviside o la logística se puede ver como haciendo un solo corte en un espacio. La posición y orientación de este corte viene determinada por los pesos de las conexiones que alimentan a la unidad, así como el umbral o sesgo (q) de la unidad. Una regla de aprendizaje modifica todos estos componentes. (El sesgo de una unidad puede entrenarse como si fuera solo otro peso de conexión asumiendo que es la señal proveniente de una unidad especial de entrada extra que siempre está encendida [Dawson, 2004, 2005].)

La red multicapa ilustrada en la Figura 4-4 es atípica porque conecta directamente unidades de entrada y salida. La mayoría de las redes modernas eliminan tales conexiones directas al usar al menos una capa de unidades ocultas para aislar las unidades de entrada de las unidades de salida, como se muestra en la Figura 4-5. En dicha red, las unidades ocultas aún pueden describirse como tallar un espacio de patrón, con coordenadas puntuales proporcionadas por las unidades de entrada, en una región de decisión. Sin embargo, debido a que las unidades de salida no tienen acceso directo a las señales de entrada, no tallan el espacio del patrón. En cambio, dividen un espacio alternativo, el espacio unitario oculto, en regiones de decisión. El espacio unitario oculto es similar al espacio patrón, con la excepción de que las coordenadas de los puntos que se colocan dentro de él son proporcionadas por actividades unitarias ocultas.

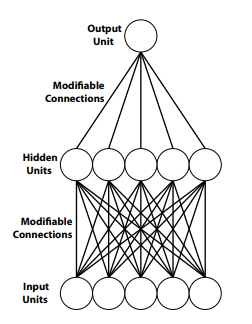
Figura 4-5. Un perceptrón multicapa típico no tiene conexiones directas entre las unidades de entrada y salida.

Cuando no hay conexiones directas entre las unidades de entrada y salida, las unidades ocultas proporcionan a las unidades de salida una representación interna de la actividad de la unidad de entrada. Por lo tanto, es propio describir una red como la ilustrada en la Figura 4-5 como tan representacional (Horgan & Tienson, 1996) como un modelo clásico. Que las representaciones conexionistas puedan describirse como una transformación no lineal de la representación de la unidad de entrada, permitiendo detectar entidades no lineales de orden superior, es por eso que una red como la de la Figura 4-5 es mucho más poderosa que aquella en la que no aparecen unidades ocultas (por ejemplo, Figura 4-3).

Cuando no hay conexiones directas entre las unidades de entrada y salida, las representaciones que sostienen las unidades ocultas se ajustan al sándwich clásico que caracterizó a los modelos clásicos (Hurley, 2001) —un sándwich coneccionista (Calvo & Gomila, 2008, p. 5): “Los sándwiches cognitivos no necesitan ser fodorianos. Una red coneccionista de alimentación directa se ajusta por igual a la metáfora sándwich. La capa de entrada se identifica con un módulo de percepción, la capa de salida con una de acción, y el espacio oculto sirve para identificar métricamente, en términos de las relaciones de distancia entre patrones de activación, las relaciones estructurales que obtienen entre los conceptos. La capa oculta esta vez contiene la carne del sándwich coneccionista”.

Una diferencia entre la ciencia cognitiva clásica y la coneccionista no es que la primera sea representacional y la segunda no. Ambos son representacionales, pero no están de acuerdo sobre la naturaleza de las representaciones mentales. “La principal lección de la investigación de redes neuronales, creo, ha sido expandir así nuestra visión de las formas en que un sistema físico como el cerebro podría codificar y explotar la información y el conocimiento” (Clark, 1997, p. 58).